曲线磨削冲程运动速度规划研究*
□ 赵 达 □ 刘福军 □ 虞梦茜 □ 胡德金 □ 许黎明
上海交通大学 机械与动力工程学院 上海 200240
1 研究背景
曲线磨削是一种精密加工方式,可加工复杂轮廓曲线,加工精度高,表面质量好。轮廓曲线的实现方式为通过圆弧截面砂轮点磨削,形成待加工曲线的包络线。加工面是以直导线、曲线组合为加工母线的轮廓曲面[1-2]。曲线磨削原理如图1所示。
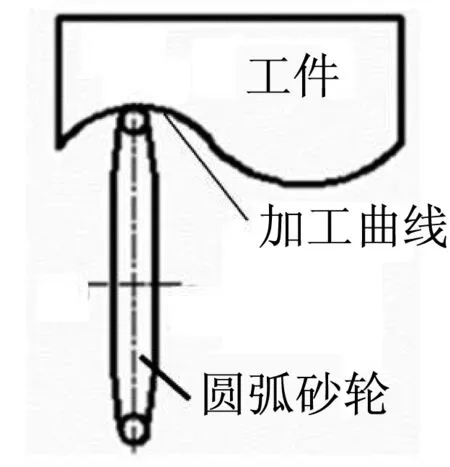
▲图1 曲线磨削原理
曲线磨削时,砂轮架往复运动,称为冲程运动,完成直导线方向上材料的去除。较高的冲程运动频率可以实现较高的曲线成形精度,并提高加工效率。与此同时,冲程运动成为曲线磨削中主要的振动激励源,会对机床产生冲击,进而影响加工精度、表面质量、稳定性等。传统的曲线磨削冲程运动由曲柄滑块机构来实现,冲程运动轨迹由机构决定,无法更改,更无法实现匀速加工。采用伺服驱动结构实现砂轮冲程运动,结合现代运动控制技术,可以实现复杂的运动学规划,为满足新的性能需求奠定了基础。
针对曲线磨削中的冲程运动规划问题,笔者首先讨论了速度规划的设计思想,然后对传统速度规划进行了分析,进而提出基于连续急动度的速度规划曲线,并基于冲程运动的循环特性提出进一步的改进方法,最后进行了不同规划的理论与试验对比。
2 速度规划设计思想
机床进给系统常用的加减速控制方法有梯形加减速、指数加减速、S形加减速[3-6]。梯形加减速分为加速、匀速、减速三个阶段,速度曲线为梯形。指数加减速分为指数衰减加速、匀速、指数衰减减速三个阶段,克服了梯形加减速的不平稳问题,但是初始加速度较大,容易引起冲击。S形加减速一般分为七段,包括加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段、减减速段,速度曲线为S形,加速度曲线呈梯形。这几种方法的急动度,即加加速度存在突变,使系统受到冲击而产生振动。急动度是描述加速度变化快慢的物理量,在加工过程中是一个重要的影响因素,如刀具加速度的快速变化会导致刀具过早磨损,使刀具切削不均匀等。
冲程运动中有两个宏观参数——行程与频率,保持相同的行程和频率,就能比较不同速度规划的性能。性能主要指最大加速度、最大急动度。最大加速度衡量速度规划对机械结构强度、电机驱动能力的影响,最大急动度衡量速度规划对系统振动的影响。
对于磨削冲程运动中的速度规划,还需要考虑加工段的速度特性,即切削行程的速度变化规律及急动度大小。加工段是否匀速与表面加工质量关系密切,但部分适合冲程运动的速度规划若要实现匀速加工,则会导致急动度剧烈变化。
综合以上分析,在速度规划的过程中主要考虑急动度的连续性、最大加速度、最大急动度、加工段的急动度大小。为了衡量不同规划间的性能差别,在设计、仿真不同速度规划时,保持行程与冲程频率相同,笔者研究方案中行程取30 mm,冲程频率为75次/min。
3 速度规划算法
3.1 传统速度规划
(1) 梯形速度规划。作为一种经典速度规划,梯形速度规划的速度和加速度曲线如图2所示。梯形速度规划中,在启动、停止、匀速前后节点均有加速度突变,如不考虑机械系统弹性,急动度在理论上为无穷大,会产生冲击干扰,易引发磨削过程不稳定等现象。
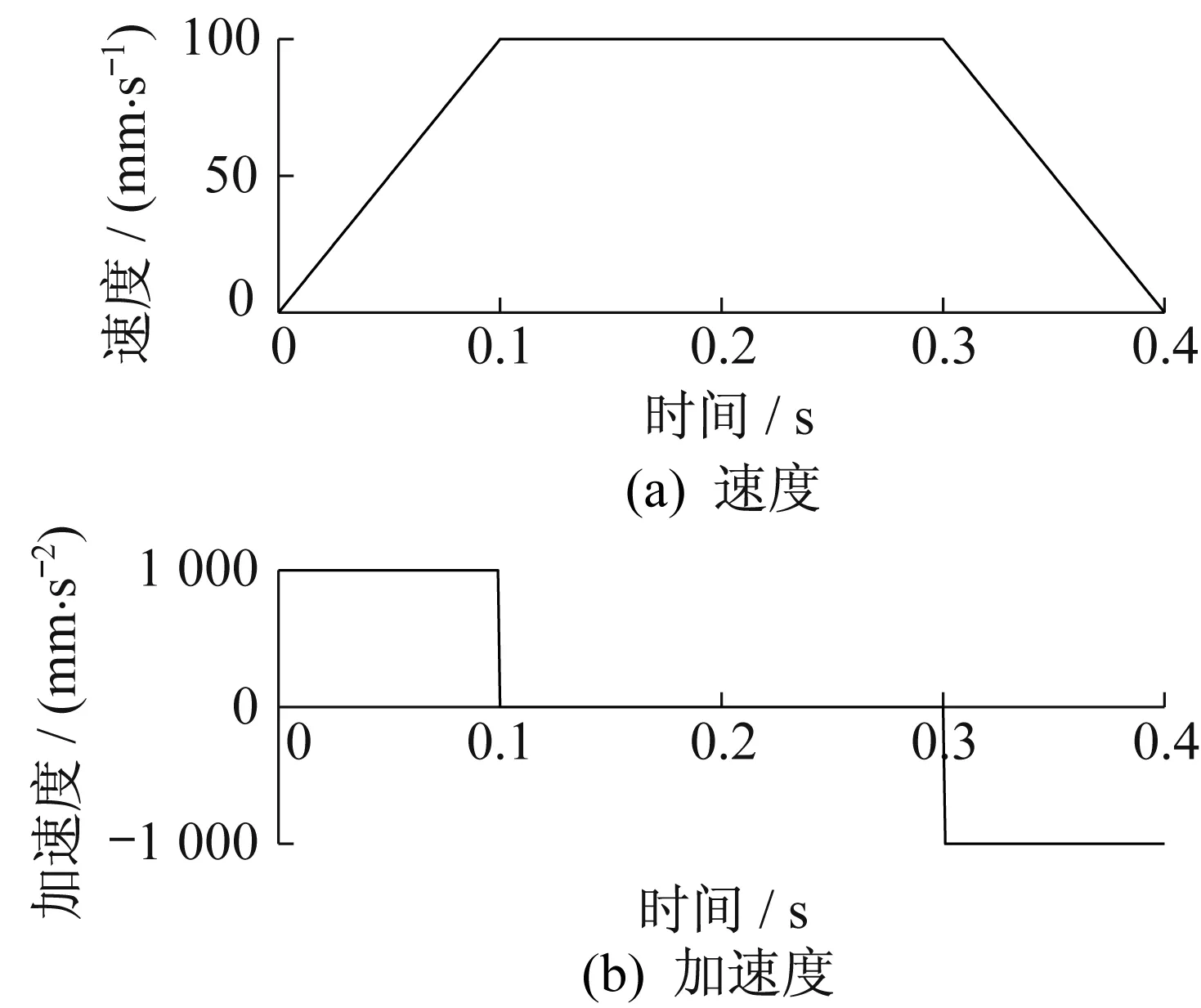
▲图2 梯形速度规划曲线
(2) 基于曲柄滑块运动的速度规划。传统曲线磨床的冲程运动由曲柄滑块机构来实现,设曲柄长为r,连杆长为l,角速度为ω,得到随时间t变化的运动位移函数s(t)为:
(1)
对s(t)求导,可以得到速度v、加速度a、急动度j函数。曲柄滑块机构速度规划曲线如图3所示。

▲图3 曲柄滑块机构速度规划曲线
由图3可以看出,曲柄滑块机构速度规划曲线相对梯形速度规划曲线更为平滑,急动度有限且连续可导,但受结构所限,运动形式固定,在加工段处的急动度最大。
3.2 基于连续急动度的速度规划
实现连续急动度的主要方法有:① 提升速度多项式的阶数[7];② 采用无限可导函数,如正弦函数等,作为速度函数基底。笔者采用正弦函数叠加梯形速度规划的方式,设计了基于连续急动度的速度规划曲线,然后通过运动特性进行优化。
(1) 正弦函数叠加梯形速度规划。由于梯形速度规划中的加速度呈阶跃变化,而三角函数一个周期的积分为0,因此可使加速过程中的加速度以梯形速度规划中的加速度为基准做一个周期的正弦波动,正弦分量积分后为0,不影响原本达到的匀速过程,且一个周期中急动度的起始点与终止点都为0,实现了连续急动度。根据上述分析,正弦函数叠加梯形速度规划的加速度方程为正弦函数加一个常数项。
速度函数v(t)为:
(2)
加速度函数a(t)为:
(3)
急动度函数j(t)为:
(4)
式中:a1、a2分别为加减速过程中的平均加速度与平均减速度;t1、t2分别为加速时间与减速时间;T为单向行程所需时间。
正弦函数叠加梯形速度规划称Ⅰ型叠加规划,设计思路为通过正弦曲线叠加梯形速度规划曲线来抵消梯形速度规划中加速度与急动度的突变。Ⅰ型叠加规划曲线如图4所示。由图4可以看出,急动度连续,整个运动过程也较为平滑,不存在无限大急动度,可以实现加工段的匀速运动,由于起始、终止加速度均为0,因此适合在单次冲程运动时使用。
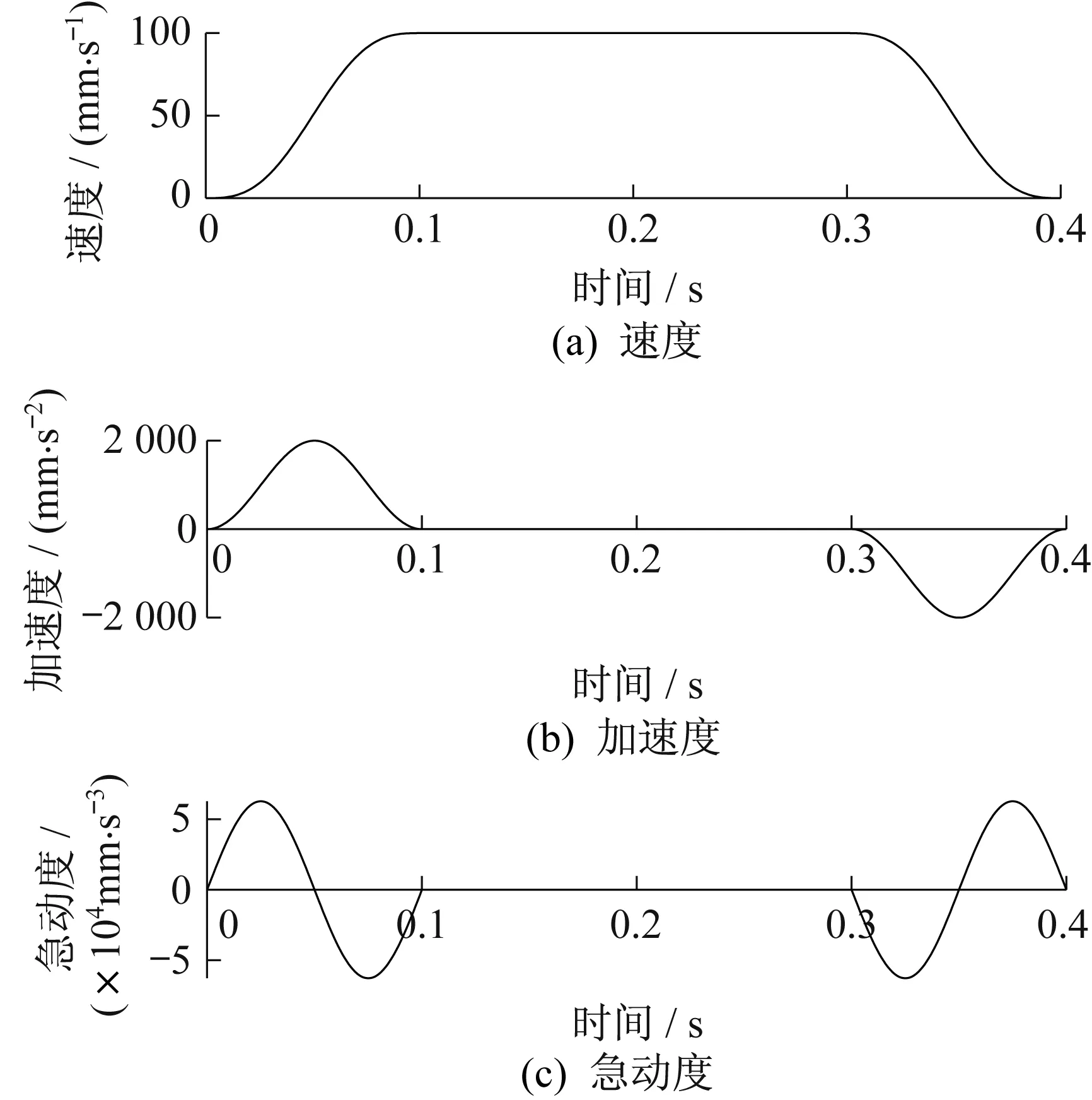
▲图4 Ⅰ型叠加规划曲线
(2) 行程端点以最大加速度过渡的速度规划。研究发现,曲柄滑块机构运动的最大急动度相对更小,主要是由于在整个行程的端点处存在加速度,而传统速度规划在起止点的加速度为0。这类似数控系统中的速度前瞻处理[8-10]。传统进给速度的规划将加工路径分为多段,每一段的路径起末速度为0,会导致电机加减速频繁,影响加工表面质量,速度前瞻处理通过提前计算下一段路径,以一个非0的速度过渡。借鉴速度前瞻处理思路,笔者提出一种适用于冲程运动的速度规划算法,行程端点处加速度不为0。
对于这类速度规划,笔者设计了端点加速度最大的正弦函数与梯形速度规划叠加速度规划,称为Ⅱ型叠加规划,行程中点急动度为0,可插入匀速加工段。同时设计了正弦函数速度规划,追求急动度最小,但在加工段附近的急动度会比较大。
对Ⅱ型叠加规划进行设计,由于行程端点可有加速度过渡,因此将端点设为加速度极大点。因为如果端点不是加速度极大点,那么在端点的前后存在加速度减小、增大的过程,这样将是低效、无意义的。由此,单个行程的过程包括减加速段、匀速段、加减速段,减加速段与加减速段对称。
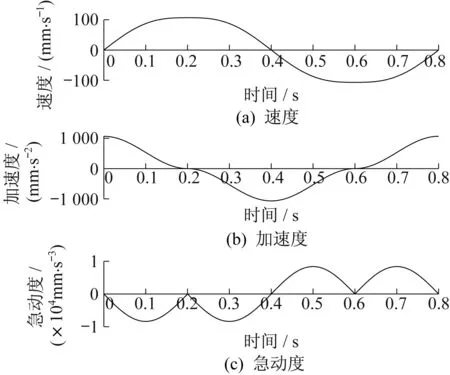
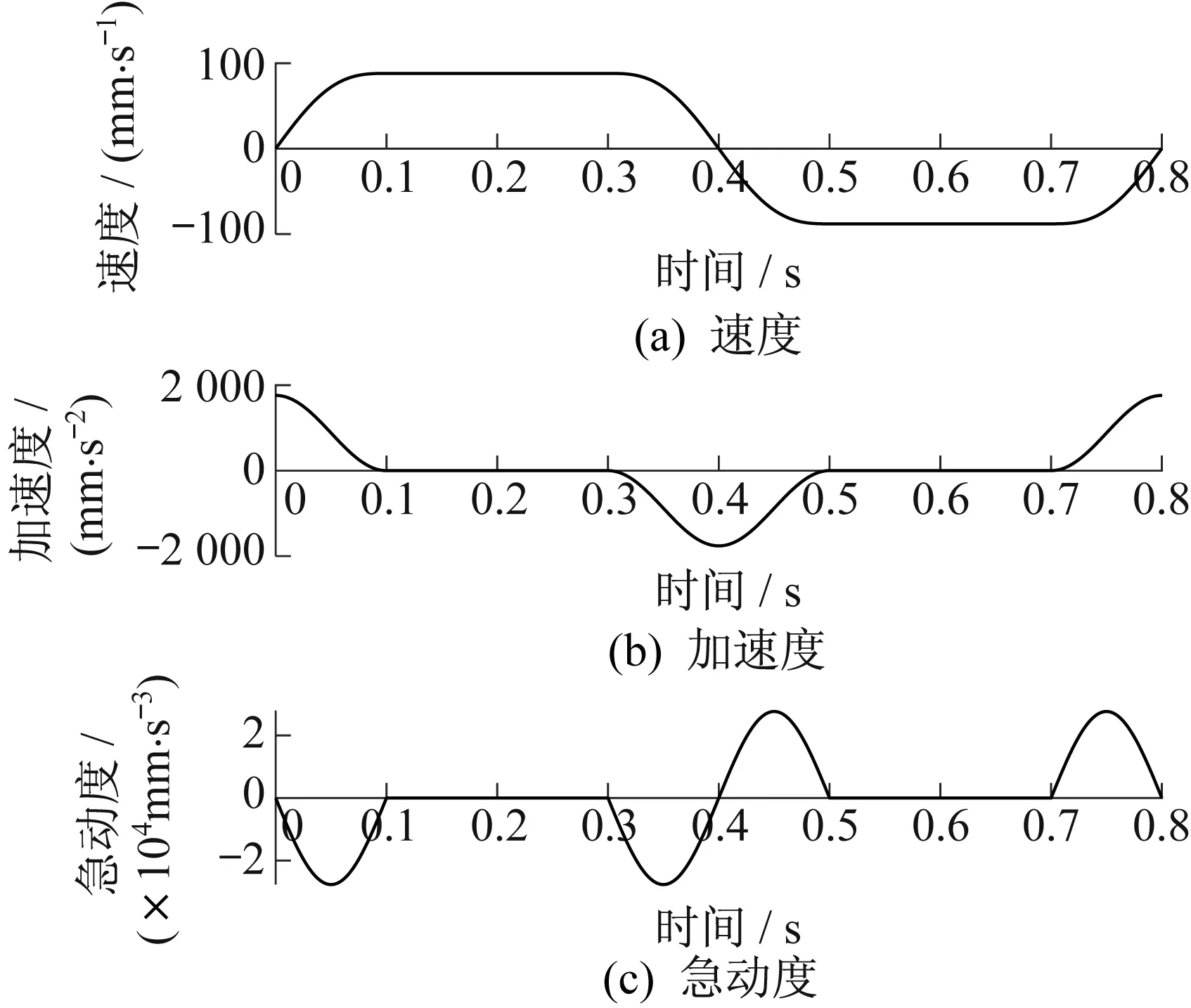
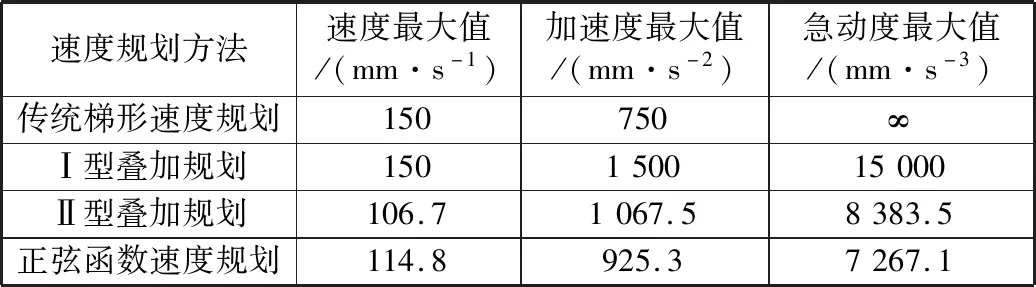
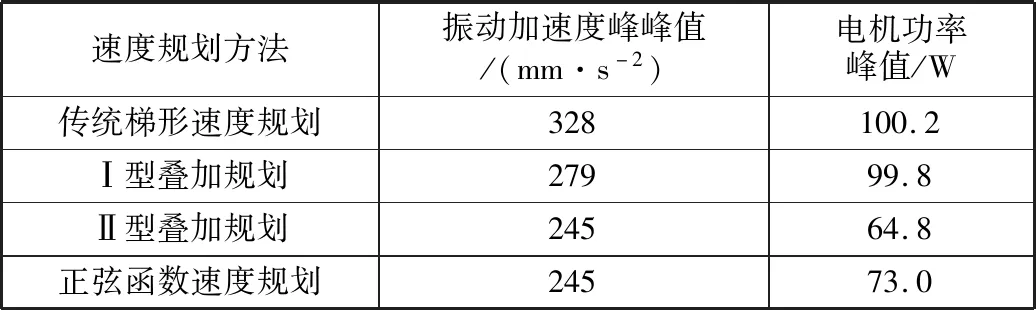
先考虑减加速段(t j(t)=-jmaxsin(πt/tm) (5) 式中:jmax为急动度最大值;tm为减加速段与加减速段的时间。 对式(5)进行积分,得到加速度函数a(t)。结合a(t)在t=0处为最大值,在t=tm处为0,可以得到加速度函数a(t)为: (6) 对a(t)进行积分,得到速度函数v(t)为: (7) 对v(t)进行积分,得到位移函数s(t)为: (8) 对于Ⅱ型叠加规划,待定参数有两个——jmax与tm,因此需要两个条件以确定整个系统的规划。在速度规划中已含有一个条件,即行程是固定的,所以只需要另一个条件即可确定唯一的速度规划。 对于所需的第二个约束条件,分两种情况:① 不需要匀速加工段的速度规划,那么减加速段结束后立即减速,由对称性可知,t=tm时行程为1/2,根据行程和时间可求得jmax,得到整个速度规划过程的解;② 需要匀速加工段的速度规划,给出需要匀速加工段的长度后,即确定了唯一的速度规划。 对于无匀速段的Ⅱ型叠加规划,由上述分析条件可解得jmax为8 383.5 mm/s3,tm为0.2 s。根据对称性,整个过程的急动度函数j(t)为: (9) 根据急动度可得加速度a、速度v,得到无匀速段Ⅱ型叠加规划曲线,如图5所示。由图5可以看出,位移、速度、加速度、急动度经过一个周期均回到初始值,即以这一周期进行循环,能够得到各参数连续,减小柔性冲击。 ▲图5 无匀速段Ⅱ型叠加规划曲线 需要设计匀速加工段时,可在上述曲线中的T/2、3T/2处插入两个匀速段,由于这两个位置的加速度及急动度都为0,因此插入匀速段不影响连续性,如图6所示。简单正弦函数速度规划不具备类似特性,因为简单正弦函数速度规划在加工段处的急动度是极大值,若插入匀速段,匀速段的急动度为0,将引起急动度突变。 ▲图6 带匀速段Ⅱ型叠加规划曲线 (3) 正弦函数速度规划。曲柄滑块机构的速度曲线存在不对称性,会导致局部急动度偏大,可采用完全对称的正弦函数设计速度规划曲线,位移函数s(t)=-Acos(ωt),A为1/2行程,正弦函数无限次连续可导,急动度连续。 针对设计的Ⅰ型叠加规划、Ⅱ型叠加规划、正弦函数速度规划,以及传统梯形速度规划,在无匀速段,行程为30 mm,冲程频率为75次/min的条件下,进行运动学性能比较,结果见表1。 表1 速度规划运动学性能比较 由表1数据可见,Ⅱ型叠加规划相比Ⅰ型叠加规划,最大加速度与最大急动度都较小。 针对表1中的四种速度规划方法,开展了速度规划性能试验,试验平台为自主开发的曲线磨削样机,如图7所示。使用开放式数控系统的电子凸轮功能实现所设计的速度规划,试验中行程为30 mm,冲程频率为75次/min。 ▲图7 速度规划性能试验平台 在冲程运动速度规划设计中,主要关注最大加速度与最大急动度。为此,在试验过程中测量两个参数,一个是砂轮架Y轴振动加速度信号,Y轴方向的振动直接影响加工质量,另一个是驱动Z轴的伺服电机功率。采用功率采集模块,通过测量电流及电压信号后计算得出电机功率。分别测量表1中四种速度规划下的振动加速度信号,如图8所示。 由图8可知,传统梯形速度规划的振动是最大的,Ⅰ型叠加规划好于传统梯形速度规划,但存在部分区间振动过大的现象,Ⅱ型叠加规划与正弦函数速度规划的振动相对较小,说明设备所受到的冲击较小。 ▲图8 不同速度规划振动加速度信号 对试验数据进行处理,得到振动加速度信号峰峰值及电机功率峰值,见表2。由表2数据可见,所设计的Ⅱ型叠加规划的振动加速度峰峰值最小,说明产生的冲击相对较小;电机功率峰值也最小,说明对电机性能的要求较低。 表2 试验峰值数据 笔者针对曲线磨削中的砂轮冲程运动规划问题,提出优化速度规划的设计思想,进而设计了基于连续急动度的速度规划方法,并针对砂轮冲程运动的特点进行了改进,使行程两端点的加速度最大。仿真结果表明,所设计的Ⅱ型叠加规划与传统速度规划相比,在运动学指标方面取得了显著的提高。试验结果表明,所设计的Ⅱ型叠加规划有效降低了柔性冲击和电机功率需求,扩大了磨削工艺选择范围,为优化曲线磨削冲程运动提供了参考。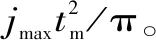
3.3 速度规划理论性能比较
4 试验研究


5 结束语

