潮流转移引发的电网连锁跳闸关键节点识别
邓慧琼,李钦彬,吴俊媛,李培强,郑荣进
(福建工程学院 电子电气与物理学院,福建 福州 350118)
近年来,电网连锁故障已成为备受关注的热点问题[1-2],关于连锁故障的分析研究中,较为普遍的思路是对连锁故障的发展过程进行复现或模拟,以连锁故障发展过程的模拟为基础构建电力系统的可靠性或脆弱性评估乃至防御连锁故障的策略等。如文献[3]根据电力系统元件的动态模型及电流保护、距离保护、低频减载、温度继电器、低压减载等5种二次设备的动作提出了一种对连锁故障进行动态模拟的方法。文献[4-5]提出了研究事故链的搜索方法。上述方法能够在一定程度上反映出连锁故障的实际发展,但计算复杂、工作量大,对模拟连锁故障的模型和方法提出了很高的要求。
实际上,连锁故障是由一系列相关的事件相继出现造成的,应尽早采取措施,以防止后续事件的发生。因此,对初始故障初始发生阶段的连锁跳闸的分析和控制极其重要。本研究从电网节点注入功率的角度研究不同节点对支路电流的影响,利用聚类分析算法筛选出对电网连锁跳闸起关键作用的关键节点,最后以IEEE 39节点系统为例对筛选的关键节点进行算例验证。
1 电网支路严重受扰的评价指标
假设某时刻电网支路Lk发生了初始故障,若电网中所有的支路都配置了电流型后备保护,则Lk被切除后,剩余电网系统中任一支路Lb是否发生连锁跳闸可根据其配置的电流保护检测到的电流量是否进入保护的动作区来判定。
假设支路Lk介于节点i和节点j之间,且Lk位于节点i的一侧配置了电流型后备保护。根据保护的定值和测量电流,可定义如式(1)所示的变量。
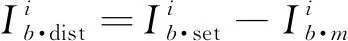
(1)


(2)
式中,ε为人为给定的一个很小的正数值,具体值根据电网实际需求确定。ε越小,代表支路受扰程度越严重。根据式(2)可对初始故障切除后电网剩余支路的受扰程度进行评价,支路只要满足式(2)即可归类到严重连锁受扰支路集。
2 初始故障后支路与节点间的关系
假设电网初始故障支路为Lk,Lk发生故障断开后,电网的结构和参数不发生变化。在近似地只考虑有功功率的情况下,电网发生潮流转移后剩余系统中的支路功率与节点注入功率之间的关系为[6]:
PL=RpPn
(3)
其中,PL表示支路Lk开断后的电网剩余系统支路的功率向量,共有l个元素;Pn表示电网中所有节点的节点注入功率向量(包含平衡节点,按电网中节点编号的顺序排列)。Rp是支路功率和节点注入功率之间的关系矩阵,其中,每个元素主要由电网结构和参数决定。根据直流潮流法的假设条件,Rp矩阵可表示为[7-8]:
Rp=SB0+λIjSB0
(4)
式中,S为支路-节点关联矩阵;B0为原电网n-1阶节点电纳矩阵逆扩展形成的节点电纳矩阵,n指电网的节点总数;Ij为l×l阶单位矩阵的第j行,l为电网发生初始故障前的支路总数。λ是由网络结构和支路电抗参数决定的一个向量,具体值的计算可参见文献[9]。
由直流潮流法的假设条件以及支路传输有功功率和支路电流之间的关系[6]可知,初始故障支路Lk断开后,电网系统剩余各支路的电流为:
I=RpPn
(5)
将式(5)的向量和矩阵展开可以得到,电网中任一支路Li的电流在支路Lk断开后的表达式为:

(6)
式(6)右侧的任一元素rijPj(j=1,2,…,n)表示节点j对支路Li的影响,而rij表示节点j对支路Li的灵敏作用。
3 严重受扰支路的筛选及关键节点的确定
根据第2节分析可知,初始故障支路断开后,系统剩余受扰支路的电流主要与节点的注入功率相关,其中少部分节点的往往起较大的影响作用。如果可以找到电网中对连锁受扰支路影响较大的关键节点,将有利于预防电网连锁跳闸的发生。本研究依据严重受扰支路的评价指标对一些受扰严重的支路进行筛选。针对筛选出来的严重受扰支路,寻找对其影响较大的关键节点,进行算例的验证分析。算法思路主要如下:
随着我国社会的不断发展,我国经济增长的速度越来越快。在过去的发展历程中,我国很多经济增长是以环境的破坏为代价而取得的,在近些年,环境保护已经成为了我国新的发展重心。随着我国对于环境保护和生态建设的重视度越来越高,林业发展成为了人们关注的重点,本文针对林木种苗的现现状进行了阐述,并对其培育技术和管护要点进行了分析。
首先,设定预想初始故障,筛选出电网中的严重连锁受扰支路,对选定的预想初始故障。利用牛顿拉夫逊潮流算法对系统进行潮流计算。针对计算结果,判断系统中是否有除故障支路以外的剩余支路满足式(2)。若有,则将该支路列入受扰支路故障集F。故障集F可表示为:
F={Li|Ii·dist<ε}
(7)
其次,针对受扰支路故障集F中的每一条支路Li,根据式(5)从Rp矩阵中提取对应的元素rijPj(j=1,2,…,n)作为特征输入量,采用聚类分析方法从电网中筛选出rijPj数值较大的节点组。这些节点组里面包含的节点即为所求的电网关键节点。
然后,引入可以衡量电网当前安全运行水平的评价指标,对聚类得到的关键节点进行算例验证:从聚类得到的两类节点集中各选出一组节点组,每组节点组包含一个PQ节点和一个PV节点。对节点组中的节点以每次增加20%的节点注入功率,重新计算电网安全运行指标值。
最后,将计算得到的数值进行详细的记录,并绘制成图,观察这些数值的变化趋势并与不同类节点得到的距离值进行比较。
本研究采用FCM聚类分析算法实现电网关键节点的划分。在进行算法分析时,假设样本的分类数目为C,第k个输入的样本表示为yk=rijPj(k=1,2,…,n),m1,m2,…,mC为聚类中不同类别的聚类中心。第k个样本对于第h类的隶属度函数用μh(yk)表示。这样一来,N个样本的聚类损失函数可以用式(8)进行表示[10]:

(8)
其中,b表示的是控制聚类结果的模糊程度其值为大于1的常数,一般取为2。[11]此外,式(8)当中还应满足所有聚类的隶属度之和为1的条件,即:
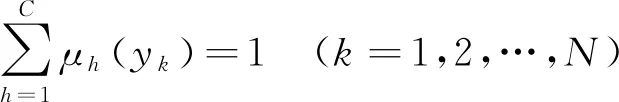
(9)
在满足式(9)的固有前提下,式(8)所示的目标函数为了取得最小值,还应满足下列两个必要条件:
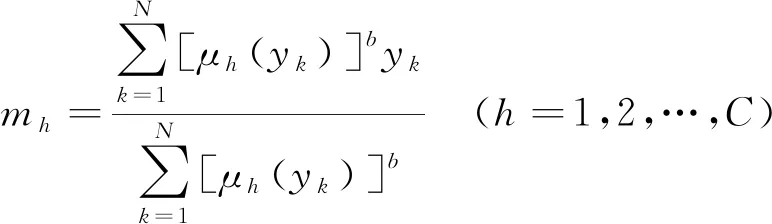
(10)
(11)
在满足了上述基本条件之后,就可以使用迭代的方法先确定几个分类的聚类中心m和隶属矩阵U[12],最后对获得的几组不同类别的节点进行分析比较,就可以获得电网中的关键节点。
得到电网中的关键节点之后,还需要验证其对于电网安全运行水平的影响能力。本研究采用电网当前运行状态下的节点注入功率与临界状态之间的节点注入功率之间的最短距离F作为电网发生连锁跳闸的安全指标[13]来验证关键节点对电网安全运行的影响。安全指标F的数学表达式如式(12)所示。


4 算例分析
为了验证,以IEEE 39节点系统为例开展算例分析。IEEE 39节点系统的接线如图1所示,系统中的元件的参数值以及电网中节点的节点注入功率数据可参见文献[14]。

图1 IEEE39节点系统接线图Fig.1 Wiring diagram of IEEE39 node system
算例分析中,假设文献[14]所给的节点功率数据为算例系统当前运行状态所对应的节点注入功率。为了计算方便,如无特殊说明,一般采用标幺值进行表示。电网中的基准容量取为100 MVA,而电网中各节点的基准电压,按文献[14]给出的IEEE39节点系统的典型数据,取100 kV。详细的算例说明如下:
(1)假定算例系统中的初始故障为支路L17-18(支路位于节点17和18之间下文同理)。支路L17-18断开后,首先利用牛顿拉夫逊法计算系统中剩余各支路的支路电流值Ii·dist,根据得到的支路电流值按式(2)判断该支路是否是严重连锁受扰支路。将系统中的满足式(2)条件的所有支路记录到连锁受扰支路集F中。其中,式(2)的ε取0.01,而电网中各支路的后备保护的电流整定值取为基态潮流状态下的电流的2.6倍,该值是为了算例演示而假定的数值。算例结果显示,线路L17-18发生初始故障后系统剩余支路共有4条严重连锁受扰支路,分别为L22-23,L19-33,L22-35,L2-30。
(2)针对F集合中的所有受扰支路,根据式(6)提取Rp矩阵中与受扰支路编号相对应的rijPj(j=1,2,…,n)数据。将提取的rijPj数据作为聚类分析算法的输入量对系统中的所有节点进行聚类划分,以评估不同的节点对连锁受扰支路的作用。从不同的聚类组中找出rijPj数值较大的节点组作为系统的关键节点组。
(3)从聚类得到的两类节点中各挑选出两个节点(PQ和PV节点),以每次增加20%的节点注入功率代入式(11)计算电网当前运行状态下的安全指标F值。
(4)对计算得到的数值进行详细的记录,观察这些数值的变化趋势并与另一类节点得到的距离值进行比较。
以初始故障支路L17-18发生后的连锁受扰支路L22-23为例,经过聚类分析计算后,得到的关键节点组有3个节点,分别为23,24和35节点,其聚类中心为0.326 6,表明其对严重受扰支路的贡献还是较大的。另一类非关键节点组得到的聚类中心为-0.014 6,说明该类节点对严重受扰支路的贡献值比较小,其中负号表明该类节点对受扰支路的贡献值与受扰支路原本的电流方向相反。按照上述方法,从关键节点组的节点中选出一PV节点和一PQ节点,修改节点的注入功率并计算对应当前电网运行状态的安全指标,将计算的结果绘制成图并与另外选出的非关键节点组得到的数值进行比较,如图2所示。图2的纵坐标是与式(12)的安全指标F值对应的,以标幺值的形式给出,而横坐标表示的是功率增加的次数,用N来表示。为了给出参照值,图2还给出了电网基态运行下的安全指标值,用基态值对应的虚线表示,该值不考虑随功率增加次数的变化而变化。另一条虚线表示的是修改非关键节点组(12,37)的节点注入功率得到的安全指标。而(23,35)表示的则是修改关键节点组中23、35两个关键节点得到的安全指标值。(24,35)和类似组别表示的含义与此相近。
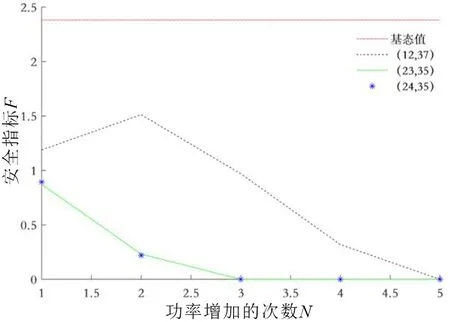
图2 支路L22-23聚类得到的关键节点验证Fig.2 Key node verification obtained by clustering of branch L22-23
从图2可以看出,随着负荷节点和发电机节点注入功率的增加,无论是关键节点组还是非关键节点组,得到的当前电网运行状态的安全指标值都是逐渐减小的,即新的电网运行状态与其对应的临界状态之间的最短距离值都是逐渐减小的,这与电网中随着节点的注入功率增加,系统越容易发生连锁跳闸的事实是相符的。而关键节点组(23,35)、(24,35)每次计算得到的安全指标值都差不多,说明了关键节点23和24对电网的安全运行指标的影响相差不大。但是与非关键节点组(12,37)相比,显然关键节点组得到的安全指标要小得多,说明对关键节点组节点注入功率增加对系统安全运行的影响更大,初步说明了关键节点在系统中的关键性和重要性。
图3以连锁受扰支路L19-33为例对图2的分析结果进行验证。连锁受扰支路L19-33经过聚类分析后,得到的关键节点组只有1个33节点(PV节点)。这时该组的聚类中心为6.32,该值即为节点33所对应的rijP数值。另一类非关键节点组的聚类中心为-4.0987e-16,可见该组非关键节点对严重受扰支路的贡献值几乎为0。本研究采用单独修改关键节点33节点和另外选取的两个非关键节点34、37进行对照。考虑到电网系统的功率平衡,又从非关键节点中挑选了两个PQ类型的非关键节点:节点8和节点20,与前一组选取的PV类型的关键节点进行组合,再去计算它们各自的安全运行指标F值。得到的计算结果如图3所示。

图3 支路L19-33聚类得到的关键节点验证Fig.3 Key node verification obtained by clustering of branch L19-33
从图3中可以看出,随着负荷节点和发电机节点注入功率的增加,无论是关键节点组还是非关键节点组,得到的电网运行的安全指标值都是逐渐减小的,数据整体呈下降趋势。而关键节点组(33)、(8,33)、(20,33)每次计算得到的安全指标值F都比非关键节点组得到的数值小,数据全部位于非关键节点组的下方。分析表明关键节点组节点注入功率的增加,对系统安全运行的影响更大,再次验证了关键节点在系统中的关键性和重要性。
如图3(a)所示,单独修改节点33的节点注入功率在第一次计算时的电网安全运行指标值还是比较大的,这可能与节点33的初始节点注入功率值较大有关系,但是后续的整体反应仍是呈下降趋势的,且都比非关键节点得到的安全指标值要来得小,数据整体上还是可靠的。
通过算例分析可见,对初始故障下的严重连锁受扰支路的筛选和关键节点的划分方法,可以得到系统中对于电力系统安全运行影响较大的关键节点。在电力系统的实际运行当中,如果支路L17-18发生了初始故障,电网调度人员应该密切注意以该支路对应筛选出的关键节点的节点注入功率。因为这些节点的功率变化对电网安全运行的影响较大。当出现紧急情况时,在条件允许时,对上述几个关键节点的注入功率采取限制措施来预防电网发生连锁跳闸,由式(6)可知可取得比较快捷有效的结果。
在实际电网中运用时,可以先针对电网中的所有支路依次进行预想初始故障设置,按本研究所提的方法将每一初始故障支路对应的严重连锁受扰支路筛选出来,并按系统节点对严重连锁受扰支路的影响进行划分,得到电网中的关键节点。将这些初始故障支路信息与对应的关键节点信息进行记录。等电网某一具体位置受到扰动或发生了具体的支路开断时,便可以对已经记录的信息进行查找,找到对应故障发生时应该注意的关键节点,对这些节点进行重点监测和限制,以防止连锁跳闸的发生。
5 结语
1)本研究提出的用于评价严重连锁受扰支路的指标综合考虑了支路的电气量与支路所配置的后备保护类型,可较为真实的反映电网的实际情况。
2)将严重连锁受扰支路的电气量与节点注入功率这一直观且可以直接获得的电气量建立联系,使得所提方法便于分析和验证。
3)通过聚类算法将预防电网严重连锁受扰支路发生连锁跳闸简化为对系统中关键部分节点的监控和限制,这对预防电网发生连锁跳闸,提高电网安全运行水平提供了便捷的方法。该方法可以为电网的进一步研究提供帮助和参考。

