深度思考：教师必备的思维品质——由“小径分绿地问题”引发的思考

□叶勤军

（杭州师范大学附属未来科技城学校，浙江杭州 311100）

小径分绿地问题（以下简称“绿地问题”）是七年级数学的常见题型.这类问题对学生掌握并运用平移知识，培养空间想象能力具有重要价值.在教学中，教师通常会引导学生用“整体减部分”的方法（以下简称“面积法”）或者平移法来求解.需要注意的是，平移法不能简单运用于所有的此类问题.请看《中学数学》2021年1 月刊中《利用平移解决的几个问题》一文中的一道例题:

例如图（图1）所示是一块草地，这块草地中间有一个十字小道，其中横向小道的宽度为1个单位，纵向小道的宽度为2 个单位长度，你能求出除十字小道外剩余草地的面积吗？

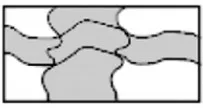
图1

作者给出的解析是这样的:

把阴影部分剪去后，空白部分平移后可以组成一个新矩形，这个矩形的长为（a-2），宽为（b-1），所以空白部分的面积为（a-2）（b-1）=ab-a-2b+2.

但是，当我们对四块空白部分进行平移，发现在拼成一块矩形后，内部出现了重合部分.由图2、图3 可以发现，重合部分是由①号和②号图形产生的.可见，图中空白部分的面积等于（a-2）（b-1）+S重合部分.

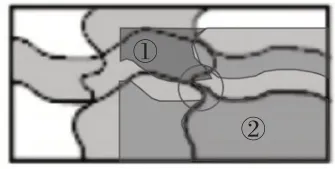
图2

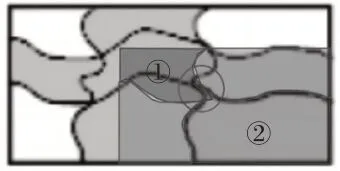
图3

为什么会出现这样的情况？笔者在深入思考和细致研究的基础上，梳理了解答绿地问题的系统方法，进而获得了有关教师素养提升的一些启示.

一、解答绿地问题的方法梳理

《中小学数学》2015 年10 月刊刊发的《运用平移求绿地面积不能被简单推广》一文，对解答绿地问题进行了较详细的分析，为绿地问题的求解提供了解题的思路和方向，但文章存在一些不足.在分析“斜路与斜路相交”时，文章先用面积法求出绿地的面积；而对于平移法，文章则认为，绿地平移后出现的中间空隙部分（如图4）是一个平行四边形，所以“若用平移，无多大实际意义，故不再求解”.然而，事实并非如此.首先，两条斜路相交，平移后所组成的图形，不一定存在空隙，也可能出现重合.其次，用平移法计算“空隙”或者“重合”部分平行四边形的面积时，探求该平行四边形边长的过程，其实也就是明确该平行四边形由来的过程，并非像文章所说的“无多大实际意义”.

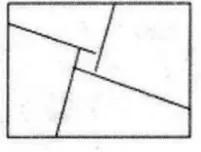
图4

此外，文章将两条小径相交的情况分成“直与直、直与斜”“斜与斜垂直”“斜与斜不垂直”三种，但没有找到不同情况的联系和共同点.其实，我们只需将情况分成“至少有一直”、“斜与斜”两种.前者用面积法或平移法计算都比较简单，若用平移法，也不会出现重合或空隙部分.后者计算稍烦琐，需要借助三角函数的相关知识，但是，用不同方法来求解，最终所得的结果是一致的，且最后得出的面积表达式，对于上述“至少有一直”“斜与斜”两者都是成立的.这就是变化当中蕴含的不变性，是问题隐含的普遍规律.

在绿地问题中，小径的数量以1条、2条的情况比较常见.1条小径的问题比较简单（其意义在于揭示了解决“绿地”问题的基本思路是转化，即将曲线和折线转化为直线，将不规则图形转化为规则图形，化繁为简），而如果小径有多条，则可转化为2 条来解答.鉴于这样的情况，以下笔者试对两条小径相交的“至少有一直”和“斜与斜”这两种情况进行阐释.

（一）至少有一直

“至少有一直”又可分为两种情况:①两条都为直（如图5）；②一直一斜（如图6）。

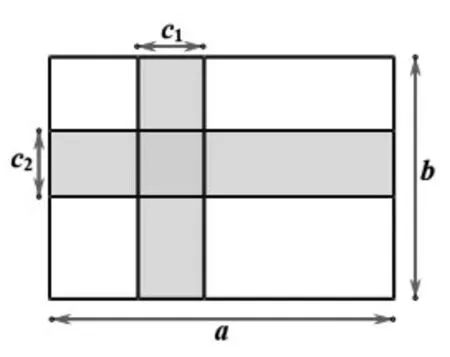
图5

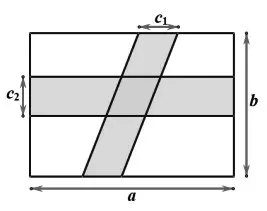
图6

对于此两种情况，若用面积法求解，两条小径重合部分，都是底和高分别为c1和c2的平行四边形，面积相等；若用平移法求解，可将原图平移成长和宽分别为（a-c1）和（b-c2）的矩形，化简得:S草地=ab-ac2-bc1+c1c2.两种方法结果相同.

（二）斜与斜

此种情况下，重合部分的平行四边形的底和高不再是c1和c2，为了求出重合部分的面积，我们需要知道倾斜小径与长方形两边的夹角α和β.

如图7，解得:

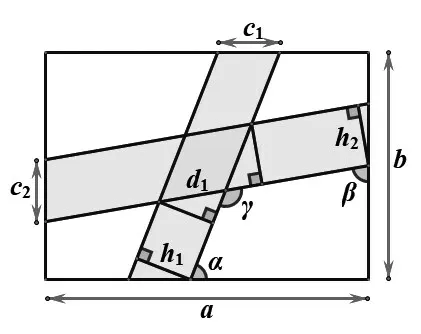
图7

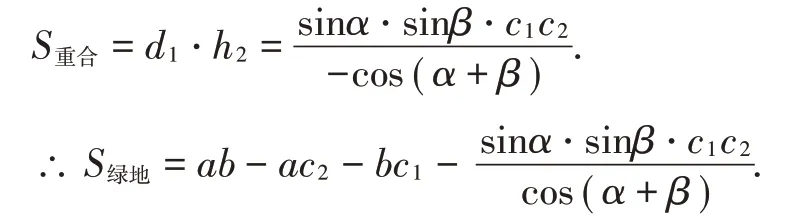
当α=90°，β=90°，即图5 所示情况，S绿地=c1c2；当β=90°，即图6所示情况，S绿地=c1c2.

由此可见，“至少有一直”只是“斜与斜”的特殊情况.下面，用平移法来研究.

通过平移拼接我们发现:当β＜90°，拼成的矩形有重合部分（如图8）；当β＞90°，拼成的矩形有空白部分（如图9）；当β=90°，恰好拼成一个矩形（如图10）.

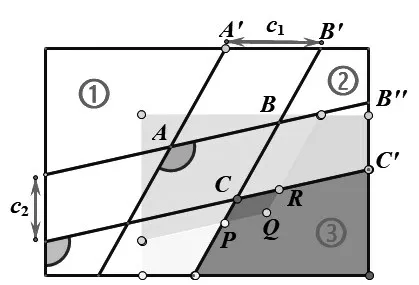
图8

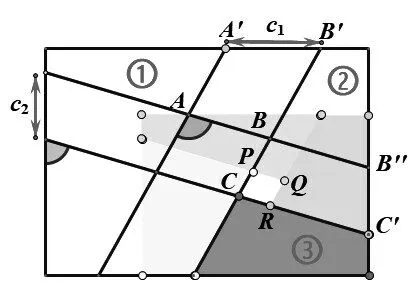
图9

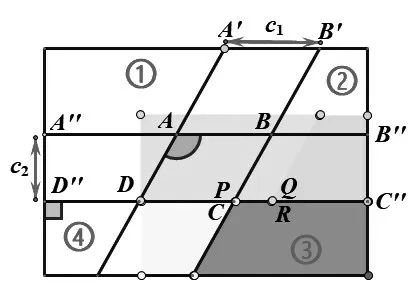
图10

下面，我们仅就β＜90°的情形进行分析.当我们将四块绿地平移至如图8所示位置，发现，四块绿地组成的图形为一块矩形，内部有一块重合部分，易证，重合部分是一个平行四边形，产生重合部分的原因是:①号四边形向右平移c1个单位长度，此时，AA'＞BB'，而AA'-BB'=QR；②号四边形向下平移c2个单位长度，此时，CC'＞BB''，而CC'-BB''=CR，故①号和③号四边形出现了重合部分.下面，我们来求解绿地的面积:

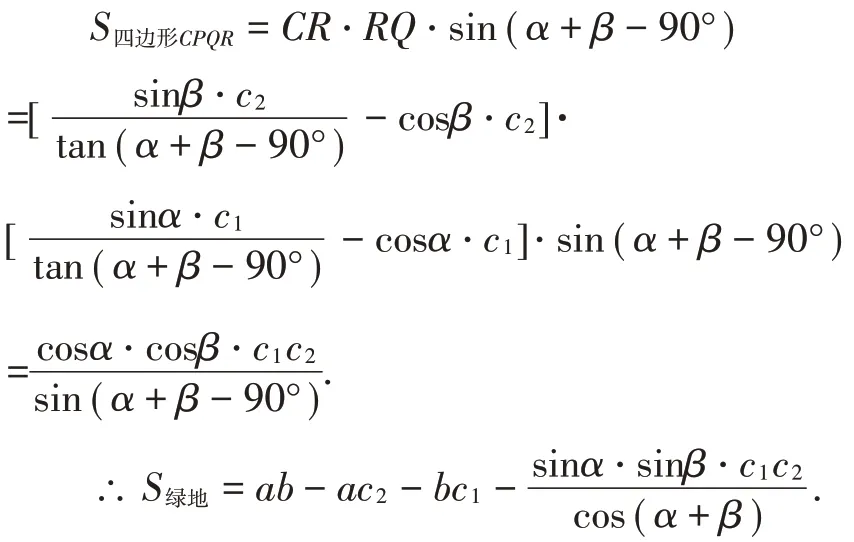
当β＞90°时，求得结果相同；当β=90°时，“斜与斜”就变成了“至少有一直”的情况，从而找到了一致性.同时可以发现，运用面积法和平移法求得的结果相同.

二、从对绿地问题的深入探索中得出的启示

养成深度思考的习惯和能力是一线教师必不可少的思维品质.

（一）要熟知并能够应用更高学段的知识来分析和解决问题

有人说，教师教什么年龄段就把自己限定在什么年龄段，初中教师只有初中生的知识水平和思维方式.随着笔者教龄的增加，这样的感受日趋强烈.教师平时接触到的问题涉及的知识点和方法局限在初中阶段，且思考问题时难免要顾及如何表述方能更易被学生接受，用目前学生已经掌握的知识成为必然.久而久之，许多高中大学阶段的知识逐渐遗忘，思维方式被局限.

这样的局面会造成什么弊端？第一，不利于问题的深入研究.教师要想对某一些问题展开探究，进行深入本质的分析，所要借助的知识往往是综合性、多方面的，仅仅依靠初中阶段的知识就会捉襟见肘，难以有效施展.第二，不利于数学知识的系统性学习.数学知识与思想是根据学段的提升逐步加深的，且彼此之间存在密切的逻辑上的联系，如果教师无法认识到一节课在以后的学段中起到的基础性作用，备课时就会产生偏差，会忽略一节课的某些重要价值，也很难做到从数学史的角度来定位和诠释一节课.这样将不利于学生对数学的系统性学习.第三，不利于教师的专业成长和自身发展.时代发展迅速，知识日新月异，要想成为一名合格的教师，我们必须具有较高的数学知识素养和文化内涵，通过终身学习，才能不与时代和学生脱节.教师如果将高中、大学的知识逐步遗忘，那么，如何对问题进行深入研究呢？自身的成长和发展必然受挫.

（二）对于问题的思考要严谨、深入和实事求是

数学研究忌讳想当然、凭感觉，即便再显而易见的问题，我们也要具备“程序化”分析的品质和能力，通过观察发现规律，通过猜想提出规律，再通过推理验证规律，这样得出的结论，才是有效和可靠的.否则，教师自己容易出错，也会误导学生.这就要求教师在研究问题时，应具备学术气质，要多方查证、深入思考，不可浅尝辄止.在深入的探究过程中，可以展露出问题的细枝末节，原先的诸多疑惑也会逐步明朗.对于一个乃至一类数学问题的分析，教师不仅要能展开，也要能够收回.一题多解、分类讨论，可以培养学生思维的严密性和创新性，但是多解归一、寻找通性通法才是返璞归真、抓住本质，才能切实提高学生的解题能力，减少其学习负担.