分布电容对高压电流互感器影响的仿真分析

赵 伟，王 宇，李 旺，沈 杰，唐建蒙

（1.中国计量科学研究院，北京 100029；2.北京云道智研科技有限公司，北京 100083；3.北京云道智造科技有限公司，北京 100083）

0 引 言

在高压下校准时，由于一次绕组会导致地电位差和绕组层间的电位差增大，从而引起容性漏电流增大、容性误差占比增大以及标准电流互感器的精度下降，因此分析分布电容对高压电流互感器的影响程度，并对其进行仿真分析具有实际意义[1]。此过程不仅有助于评估测量结果，而且也有利于优化器件结构[2]。根据国外有关单位在此方面的相关研究成果，可将电流互感器中的分布电容进行划分归类，但由于电容的复杂性难以通过直接试验的方式对分布电容进行准确测量，因此需要借助有限元仿真的方法，并通过仿真分析指导电流互感器的结构优化，进而减小分布电容。本文也将在相关研究成果的基础上研究和分析电流互感器的原理，通过建立等效电路模型分析互感器的性能，以此研究各分布电容对校准精度的影响，确定其中的关键因素[3]。在此过程中，通过计算得到互感器的绕组间电容和分布电感等参数，以此为电路分析提供准确的参数值。

1 研究方法

1.1 电路的等效变换

电流互感器原理上跟单相变压器类似，其稳定运行时的基本方程为：

式中：Z1表示为一次侧漏阻抗，对应的一次侧绕组电阻为R1，一次侧绕组漏电抗为Xσ1；Z2为二次侧漏阻抗，对应的二次侧绕组电阻为R2，二次侧绕组漏电抗为Xσ2；Zm为电流互感器的励磁阻抗，与铁损对应的励磁电阻为Rm，与铁芯磁路磁化特性对应的励磁电抗为Xσm。

为了获取T型等效电路，在保持二次绕组磁动势、有功功率以及无功功率不变的条件下，对二次侧的参数进行折合[4]。得到折合后的基本方程为：

通过以上的折合，使一次侧绕组和二次侧绕组之间建立了电路上的联系。根据折合后的基本方程式，可以得到电流互感器的T型等效电路[5]。T型等效电路的作用是采用电路的方式来模拟电流互感器，使分析计算得到简化[6]。但是T型等效电路在分析绕组间电容和绕组对地电容对电流互感器测量精度影响时，连接关系不够清晰[7]。为解决此问题，本文根据电流互感器基本方程式获得一次绕组和二次绕组的回路方程为：

Zm为一、二次绕组间的互阻抗，忽略励磁电阻的影响，则Zm=Xm/k=M，M为一、二次绕组间的互感，据此建立电流互感器的等效电路如图1所示[8]。

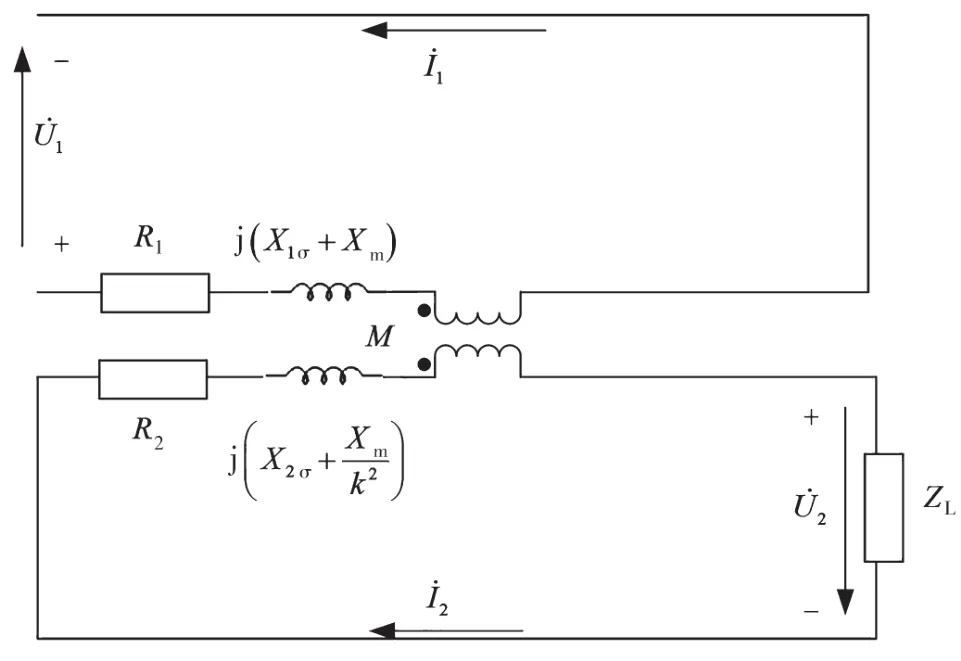
图1 变换后的电流互感器等效电路

图1中R1、R2分别为一、二次绕组电阻，R1取0.42 mΩ，R2取 11.44 Ω。

1.2 理想电路仿真

理想电流互感器的条件为一次侧漏感Ls1=0，二次侧的漏感Ls2=0，一次侧和二次侧的耦合系数为1，二次侧的电阻R2和负载Rz2均为0[9]。

在理想电流互感器电路模型中，一次绕组自感L1=230.277 799 μH。在此过程中，假设耦合系数为1的理想情况，M12=500×L1=115.138 899 5 mH。一次侧加载电流激励，电流幅值为500 A，频率为50 Hz。计算步长取1e-7s，即一个周期2×105个计算点，计算10个周期，以此种方式完成对理想电路的仿真。

1.3 结合寄生电容参数的电路仿真

在电流互感器原理图的基础上，搭建无电屏蔽，考虑对地电容的电流互感器仿真电路。设置AC电流源幅值为500 A，频率为50 Hz，Rz1=100 Ω，通过Rz1将一次侧的电压抬升至有效值约35 kV[10]。此外，考虑4个绕组自身的电阻、绕组间的互感、绕组间的电容以及各绕组的对地电容。计算步长取1e-7s，即一个周期2×105个计算点，计算10个周期。

2 计算结果与讨论

2.1 寄生电容提取

通过电磁场模型的求解，计算结果如表1所示，对角线上为绕组的对地电容，非对角线上为绕组间的电容。

表1 变流器绕组的电容矩阵

2.2 电路仿真

2.2.1 理想电路仿真

对理想电路进行仿真，得到一次侧和二次侧的电流曲线，一次侧电流有效值为I1=3.535 532 12 A，电流互感器的变比为Kn=500，此时电流互感器的比差为0.000 055 2%，角差为0.0°。

理论上，理想电路中，二次侧的比差和角差均为0，由于电路的数值计算存在一定的误差，因此计算结果中角差为0，比差不为0，但比差为0.000 055 2%，可满足精度要求。

2.2.2 结合寄生电容参数的电路仿真

根据仿真结果，可知一次侧电流有效值为I1=3.535 532 12 A；二次侧电流有效值为I2=7.065 982 4 A。当Kn=500时，得到电流互感器的比差为-0.071 867 542%，角差为-0.007 02°。寄生电容有自电容 Cgpa1、Cgpa2、Cgpb1、Cgpb2、Cgsa1、Cgsa2、Cgsb1以 及Cgsb2，同 层 互 电 容 Ca1、Ca2、Cb1、Cb2、Cc1、Cc2、Cd1以及Cd2，异层互电容Cfirst_hu1、Cfirst_hu2、Csecond_hu1以及Csecond_hu2。在完成上述计算后，采集回路中各寄生电容上的电流有效值，如表2所示。

表2 各寄生电容上的电流有效值

在导出各寄生电容上的电流有效值后，即完成分布电容对高压电流互感器影响的仿真分析。

3 结 论

在完成分布电容对高压电流互感器影响的仿真分析后，可知在寄生电容的干预下，高压电流互感器受到紧邻载流导体的影响，造成一、二次侧电流存在非理想的变化，角差和比差均不为零，这也证明了寄生电容参数对电流互感器确实存在影响，电路仿真有效。