结合降噪卷积神经网络和条件生成对抗网络的图像双重盲降噪算法

井贝贝，郭 嘉，王丽清，陈 静，丁洪伟*

（1.云南大学信息学院，昆明 650500；2.云南省广播电视局科技处，昆明 650000）

（∗通信作者电子邮箱dhw1964@163.com）

0 引言

图像去噪一直是计算机视觉领域的研究热点，在不断被提出的新算法的推进下该领域的研究得到了稳步发展。一般而言，大多数的图像降噪模型都在降噪效果和计算效率之间取舍，如:文献［1-2］中的牺牲计算效率的马尔可夫随机场（Markov Random Field，MRF）模型，文献［3-4］中的非局部自相似（Non-local Self-Similarity，NSS）模型。为克服传统模型的弊端，文献［5］提出了一种收缩场级联（Cascade of Shrinkage Fields，CSF）方法，使用的模型框架能够利用许多线性滤波器影响非线性函数，并且具有很高的并行性，该方法极大地提高了模型的计算效率。此外，文献［6］针对核范数极小化平均正则化所导致的自身受局限而提出的加权核范数最小化（Weighted Nuclear Norm Minimization，WNNM）算法要优于文献［7］的三维块匹配（Block Matching 3D，BM3D）算法。文献［8］中提出的去噪卷积神经网络（Denoising Convolutional Neural Network，DnCNN）模型，使用深度卷积的残差学习对图片进行盲降噪，克服了文献［5，9-10］中TNRD（Trainable Nonlinear Reaction Diffusion）单一噪声水平下对应单一模型的缺点。

为了进一步提高图像降噪的性能，文献［11］中提出了多降噪器最优组合（Optimal Combination of Image Denoisers，OCID）模型，将两个或者三个经典降噪模型相组合来提升降噪效果，最终BM3D 和DNCNN 组合的降噪效果最为明显，但模型计算效率并不理想。文献［12］中则是结合平稳小波变换和卷积神经网络的优势，将图像进行尺度为1 的平稳小波分解后把高、低频分量送入不同的残差网络中训练，测试阶段使用逆变换获得预测图像，且计算效率相较于文献［11］算法有所提高。文献［8］算法和文献［13］算法一样都是采用残差学习策略，不同的是文献［13］算法使用空洞卷结构提取全局信息，并结合多尺度特征以恢复图像细节。文献［14-15］提出了一种较为新颖的降噪方法，均对图片进行分区处理，其中:文献［14］提出了一种新型降噪超分辨的插值结构，将基于纹理特征的超分辨算法和基于差异曲率的降噪算法相结合，能够将含噪图像分为平滑点区域、噪点区域及边缘点区域，然后实现对含噪图片的超分辨；文献［15］中首先通过反向传播（Back Propagation，BP）神经网络预测并区分超声图像中的噪声区域和组织区域，然后与双边滤波器结合实现对超声图像的自适应滤波，不可避免的是文献［14-15］算法均存在计算效率低的缺点。文献［16］中提出了FFDNet（Fast and Flexible Network based on image Denoising）模型，虽能在少量无重复性结构上获得良好的降噪效果，但却要求降噪图像和训练所用的图像存在相似结构。文献［17］中则利用凸优化和神经网络技术将多个降噪器的降噪图像进行加权以提升降噪效果，但计算效率仍有待提高。

文献［11-17］方法虽然相较传统方法性能有一定程度的提高，但在计算效率和降噪效果权衡上仍有很大的提升空间，本文中将改进的DnCNN 模型作为条件生成对抗网络（Conditional Generative Adversarial Net，CGAN）的生成器，DnCNN 中包括 由卷积 层（Conv）、批标准 化（Batch Normalization，BN）和线性整流单元（Rectified Linear Unit，ReLU）组成的残差块，能够很好地捕获图像噪声分布。将加噪图片剔除生成器输出的噪声分布后与未加噪的干净图片通过判别器形成博弈，在博弈过程中隐层参数不断调整使得最终模型达到博弈平衡。实验结果表明，本文所提出的算法在DnCNN现有的优势上进一步提升了模型的降噪效果。

本文算法的特点有:1）将残差学习的DnCNN 模型改进后和CGAN 相结合，残差提取能力更强；2）采用将三个单一水平降噪模型并联组成盲降噪模型，泛化能力更强；3）具有较浅的模型深度（19层）并适用于GPU并行计算，计算效率更高。

1 相关工作

1.1 DnCNN模型

深度学习被大量应用于图像降噪算法［18-21］。DnCNN 模型是在修改VGG19（Visual Geometry Group network 19）的基础上通过调整卷积核为3×3 并去掉所有的池化层获取的。该模型不再是简单地从加噪图像c=m+u中学习映射函数F(c)=m，而是通过将卷积、ReLU 和BN 层相结合不断对隐层参数训练得到R(c)=u的映射，即从加噪的图片中学习噪声的分布，然后将学习到的噪声分布与真实噪声分布的均方误差（Mean Square Error，MSE）作为损失函数，类似于文献［18］提出的EPLL（Expected Patch Log Likelihood）和文献［6］中提出的WNNM 噪声消除策略。DnCNN 的模型架构如图1 所示，损失函数如式（1）。

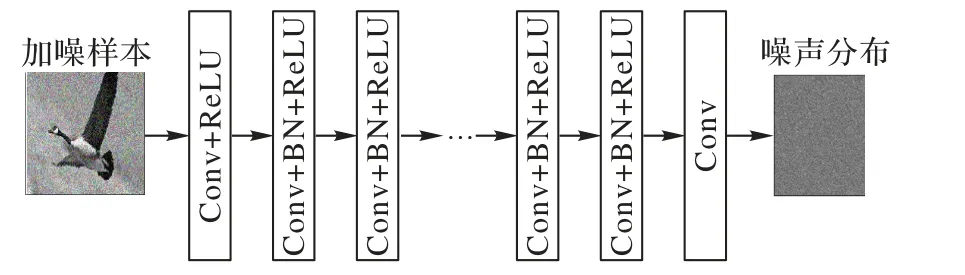
图1 DnCNN模型架构Fig.1 DnCNN model architecture

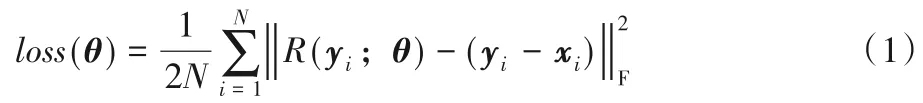
式中:xi和yi分别表示样本和加噪样本；R(yi；θ)表示学习到的噪声分布；N表示样本数；θ表示需要训练的参数，后续使用自适应矩估计（Adaptive moment estimation，Adam）优化器进行优化。

1.2 CGAN

文献［22］中提出的生成对抗网络（Generative Adversarial Net，GAN）是由生成器和判别器两部分组成，生成器（Generator，G）利用噪声生成和样本尽可能相似的图像以骗过判别器（Discriminator，D）。D通过对样本和生成图片的判别来不断提高判别的准确度，从而生成器和判别器形成博弈，如式（2）。文献［23］中所提的CGAN 是在GAN 的基础上改进而来，针对GAN 不可控的缺点加入了监控条件s，CGAN 模型结构如图2所示，损失函数由式（2）变为式（3）。

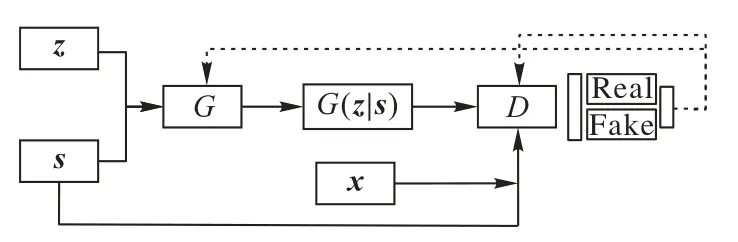
图2 CGAN模型架构Fig.2 CGAN model architecture

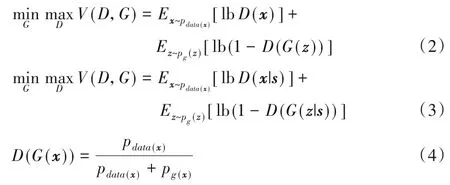
式中:x表示来自数据集的样本矩阵，z表示噪声矩阵；G(z)表示生成器生成的图片，D(x)和D(G(z))分别表示对样本和生成图片判别后的真实概率；s表示监控条件。对于判别器而言，D(x)和D(G(z))的期望值分别是1 和0，然后把这个结果反馈给生成器和判别器，生成器通过调节隐藏层的参数使得D(G(z))趋于1 以骗过判别器，判别器则通过对隐层参数的调节来提高判别的准确率。在不断的博弈当中，生成器和判别器趋于平衡状态，最终判别器对于真实数据和生成数据的判别结果都接近0.5，此时目标函数式（4）得到最优解，式（3）在此基础上增加了监控条件s。

1.3 Dropout层抑制过拟合

过拟合问题是深度学习中经常遇到的问题。用于解决过拟合问题的Dropout 层与传统的受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）使用权重衰减策略不同，Dropout层是对每个隐含节点的权值设置一个服从Bernoulli分布的约束条件。如果约束条件被激活，则该节点以p概率被舍弃，以此使得模型权重稀疏化从而达到解决过拟合的目的。标准网络如图3 所示，Dropout 层的使用如图4 所示，式（5）～（6）是增加Dropout层前后神经层传递数据方式的变化。

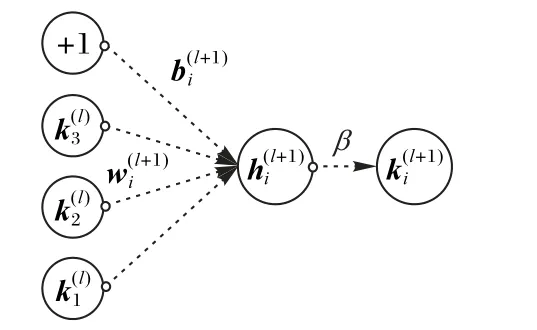
图3 标准网络Fig.3 Standard network

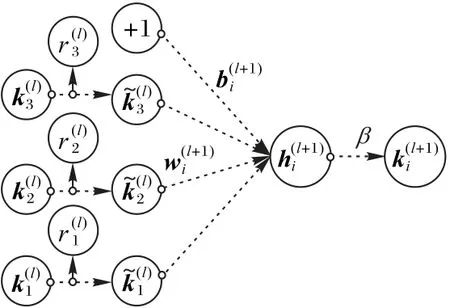
图4 Dropout层的使用Fig.4 Use of Dropout layer

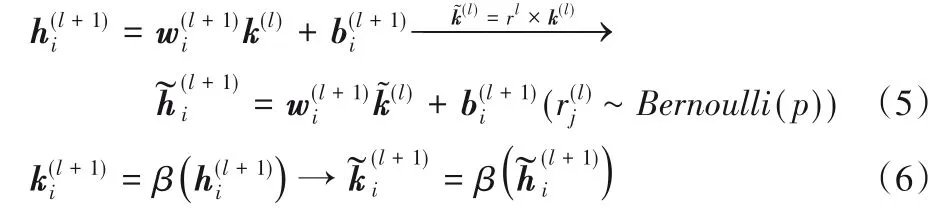
式中:k(l)、rl、l分别代表神经元的传递数据、Dropout的概率、层序数、β分别代表权值矩阵、偏置矩阵和激活函数。

2 本文图像双重盲降噪算法

2.1 模型架构及损失函数设计

生成器依据DnCNN 的特点，本文在VGG19 的基础上移除了所有的池化层，并且将各层的卷积核设定为3×3。在第d层的感受野是(2d+1)×(2d+1)，仍采用0 填充的方式处理边界伪影。图像降噪中，随着模型深度的增加会出现计算效率低、过拟合、模型退化等问题。计算效率低可以通过并行GPU 运算来解决；过拟合可以通过适当正则化、添加Dropout层解决；模型深度增加导致的模型退化的问题，也可以通过改变模型结构使用ResNet 网络来解决。对于模型中单一层的输出并不能充分捕获图像特征的分布规律，本文改进并使用了文献［24］提出的改进残差密集块（Improved Residual Dense Block，IRDB），其作用是将浅层与深层的输出相叠加继续传递，这样就防止了浅层特征在传递过程中消失，进而提高了生成器捕获噪声分布的能力，生成器中IRDB 结构如图5 所示。判别器的设计相对比较简单，由两组连续的Conv 层、BN 层、LeakyReLU（Leaky ReLU）层、概率为0.5 的Dropout 层，外加Flatten、Dense 层组成。对于贴片尺寸，本文模型在参考了文献［8］中根据不同的噪声水平和感受野设置样本贴片的大小，文献［8］通过实验给出了固定噪声水平（δ=25）下几种降噪模型样本贴片的有效尺寸，并根据噪声水平和感受野设置输入模型贴片为40×40，δ=25 时不同模型的有效贴片尺寸如表1 所示。EPLL 与文献［8］模型感受野相近，其有效样本贴片为36×36，文献［8］模型的感受野为35×35，有效样本贴片为40×40。本文模型的噪声和文献［8］模型同为15、25、50三个水平，但本文模型的感受野略大于文献［8］模型的35×35，为39×39，故将样本贴片的有效尺寸设置为43×43。整个模型的结构如图6所示，图中DP表示Dropout层。

表1 δ=25时不同模型的有效贴片尺寸Tab.1 Effective patch sizes of different models when δ=25

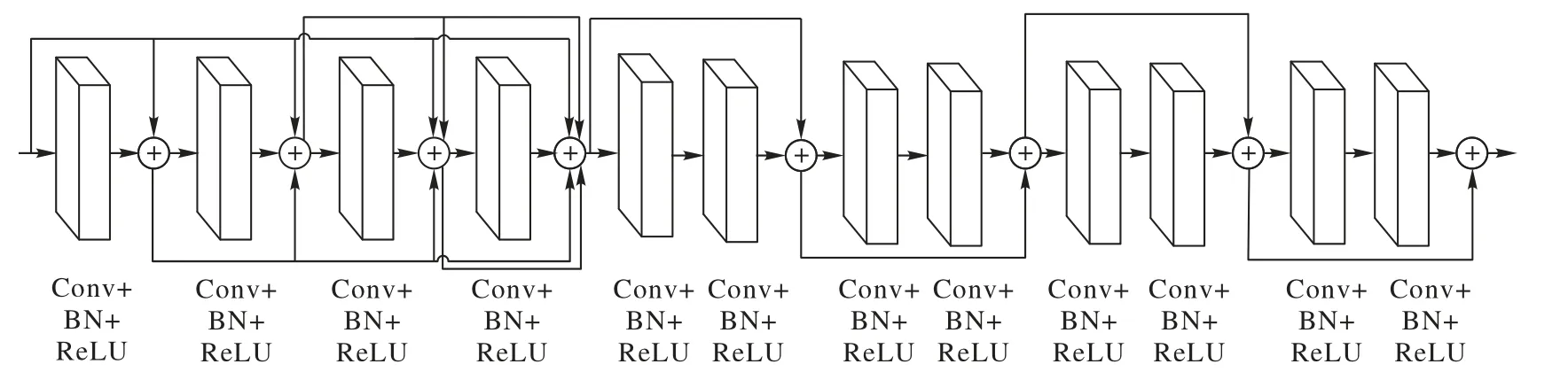
图5 生成器中IRDB结构Fig.5 IRDB structure in generator

由图6 模型架构所示，首先将加噪样本y喂入生成器，生成器捕获噪声分布R(y)，然后以真实样本和y-R(y)的MSE作为DnCNN 损失，即生成器损失，计算式如式（7），值得注意的是本文并不是捕获图像分布R(y)=x，而是捕获噪声分布R(y)=v。模型损失是在经典GAN 损失函数基础上改进而来的，生成器求出生成器损失和生成器可训练参数之间的梯度，然后由生成器的优化器进行优化。判别器则根据对标签和生成输入的判别结果求出判别损失，优化过程和生成器类似，后将判别结果反馈给整个模型，使得模型参数得到优化，计算式如式（8），最终模型在博弈当中不断优化。

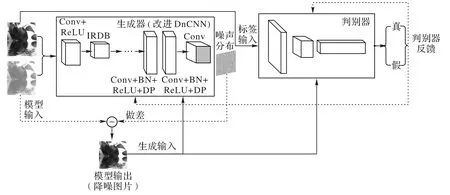
图6 整个模型的架构Fig.6 Architecture of whole model

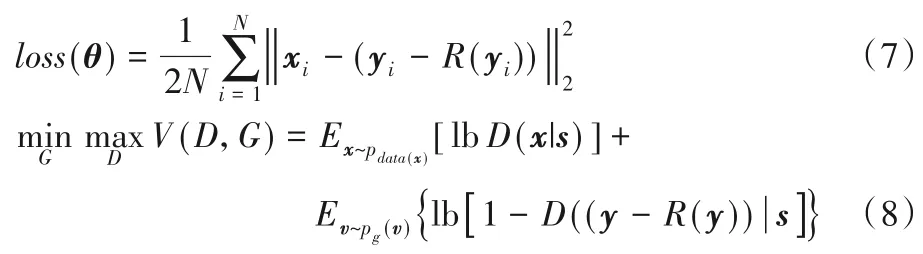
式中:xi、x分别表示样本和样本矩阵；yi、y分别表示加噪样本和加噪样本矩阵；R(yi)、R(y)分别表示捕获的噪声分布和捕获的噪声分布矩阵；s、v分别表示监控条件和噪声矩阵。通过式（7）～（8）的不断优化，生成器对噪声的捕获能力不断增强。

2.2 IRDB有效性的论述

在生成器中最重要的结构是IRDB，这里对其起作用的原因进行解释。为方便讨论，假设不使用任何激活函数，且输入输出维度一致。从前向传播来看，第l2层残差块的输出由式（9）表示，不难看出，任意低层的特征可以直接映射到高层，使得高层对于图像特征分布的捕获更加充分，从而抑制了特征在传播的过程中退化。从反向传播来看，最终的损失对某底层的梯度如式（10）所示，表明反向传播的错误信号可以避开中间权重直接传播到低层，这样就避免了梯度消失。

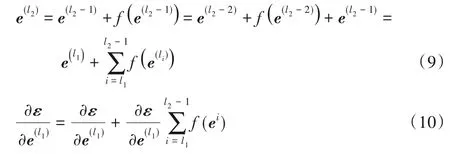
式中:li表示层序数；f表示残差函数（学习直接沿网络传播的映射）表示第l残差块的输出矩阵；ε表示损失矩阵。

2.3 批量大小和学习率的选择

批量随机梯度下降（Stochastic Gradient Descent，SGD）的权重更新如式（11）～（12）所示，从中不难看出权重的更新由学习率η、批量大小n、梯度∇loss(x，wt)共同决定。

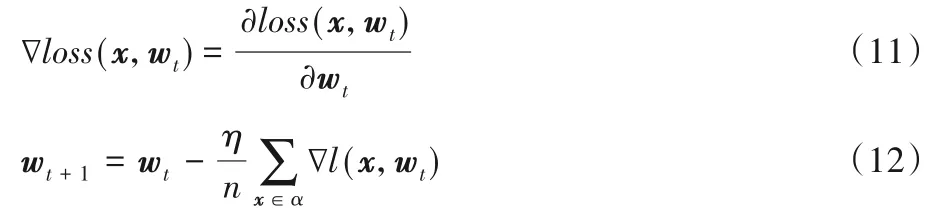
式中:∇loss(x，wt)表示某个样本的损失矩阵对于权重矩阵的梯度，由该样本对权重求导而得；wt表示权重矩阵；x表示样本矩阵；η表示学习率；n表示批量大小。

学习率直接决定着权重更新的步长，它对模型的影响体现在初始学习率和学习率变换方案两个方面。初始学习率过大则会导致模型不收敛，过小则会导致模型收敛慢甚至不收敛，为此只有通过搜索法来确定最佳的学习率。针对学习率变换方案，虽然文献［25-26］中证明经过调优的随机梯度下降（SGD）算法可能会取得更好的训练效果，但学习率是一个特别敏感的参数，保守起见本文采用的是Adam 调优策略，给定初始学习率η为10-3，迭代步长为5 200，迭代率为0.5，即每迭代5 200 步学习率降为原来的1/2。文献［27］表明，批量大小n对模型影响如图7 所示，在一定范围内增加n值会有助于提高模型的稳定性，但是随着n值的继续增加模型性能会下降；文献［28］表明，小的n值携带的噪声有助于逃离sharp minimum 从而达到flat minimum，后者具有更好的泛化能力，批量大小n对极值的影响如图8 所示；文献［29］表明，随着训练时间的增加，大的n值仍会收敛到flat minimum 点。由此可见，在训练时间足够长的情况下增加n值会给模型性能带来良性影响，基于显卡运算能力本文选用的n值为128。具体参数设定如表2所示。

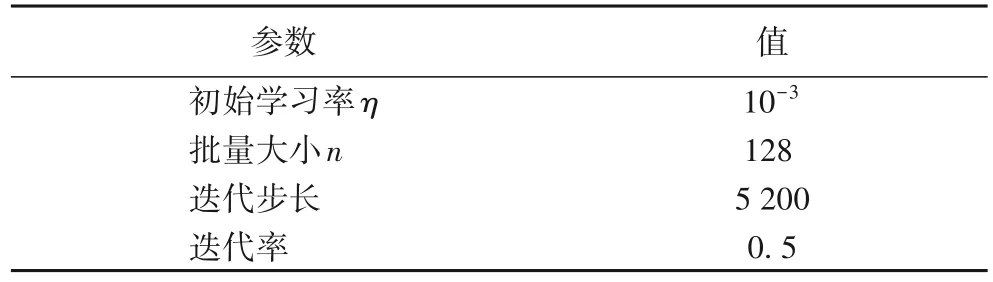
表2 部分超参数设定Tab.2 Partial hyperparameter setting

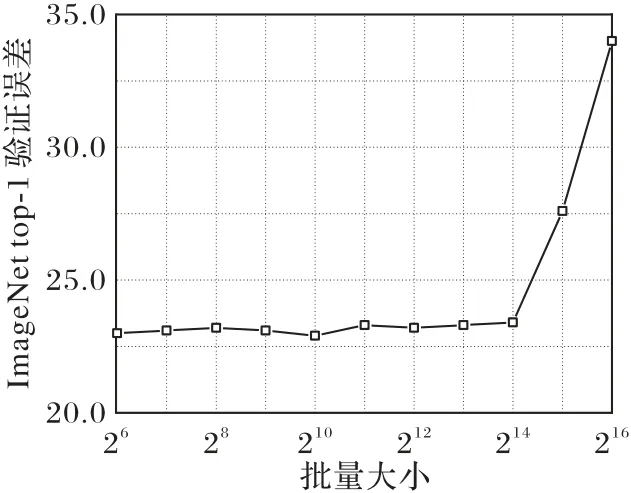
图7 批量大小n对模型影响Fig.7 Impact of batch size n on model

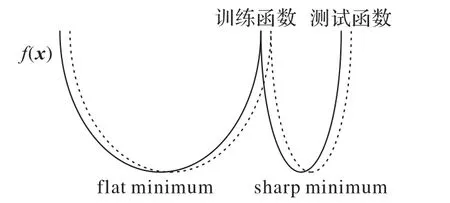
图8 批量大小n对极值的影响Fig.8 Influence of batch size n on extremums

2.4 Dropout层对模型的影响

DnCNN 模型的降噪原理和文献［5］的观点不同，文献［5］是基于F(y)=x的映射，而DnCNN 则是基于R(y)=v的映射。为了控制变量，实验均是基于F(y)=x的映射，在分别使用SGD 和Adam 优化器情况下，观察模型损失。为验证Dropout 层具有解决过拟合问题的能力，本文搭建了一个由一个Flatten 层加一个Dense 层，外加一个概率为0.4 的Dropout层，最后再加一个Dense 层组成的模型来验证。该模型除最后一层的激活函数为Softmax 外其他激活函数均为ReLU，输入图片大小为28×28。

Adam 优化器和SGD 优化器下的模型损失分别如图9～10所示。由图9～10 可以看出，随着迭代次数的增加，带Dropout层的损失在不断下降，而无Dropout 层的损失在第7 次迭代时趋于分离，即训练损失在下降，真实损失却在上升，模型的泛化能力不再提升，出现过拟合，在Adam 优化器下更加明显，从而表明Dropout层能够有效解决过拟合问题的能力。

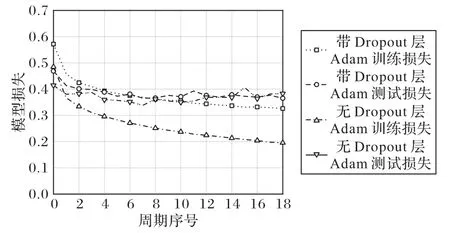
图9 Adam优化器下的模型损失Fig.9 Model loss under Adam optimizer

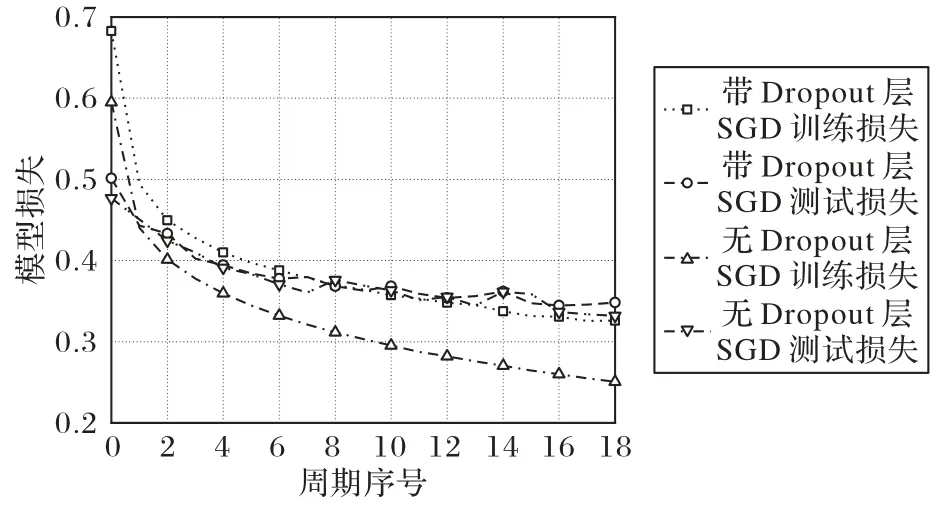
图10 SGD优化器下的模型损失Fig.10 Model loss under SGD optimizer

3 实验与结果分析

本文训练模型所采用的两个优化器均是Adam，初始学习效率为10-3，迭代周期为1 200。本文训练的模型采用的噪声水平分别是15、25、50，改进后的DnCNN模型作为生成器输入的图片采用43×43 的样本贴片，模型深度降为19 层，其中:0层采用Conv 加ReLU 结构；1～11 层为IRDB 结构；12～18 层均是由Conv、BN 和激活函数ReLU 所组成，为防止模型过拟合，第16、17 层的激活函数后添加了概率为0.5 的Dropout 层（一般加在深卷积层后，因为此时参数较多更容易产生过拟合），均采用3×3的卷积核，卷积核数均为64，采用残差学习策略。判别器的设计和模型架构中的描述一致。

实验所用到的操作系统为Windows 10，CPU 为intel 酷睿i7-9700k，GPU 为 RTX2080TI。训练模 型环境 为tensorflow2.0，python3.7。本文中所使用的激活函数（ReLU和LeakyReLU）均为默认参数。在训练单一模型阶段采用的图像质量评价指标和DnCNN 一样都是峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）（单位为dB），PSNR 是基于像素误差对图像进行评估，其值越高表示去噪质量越好。PSNR计算式如下:

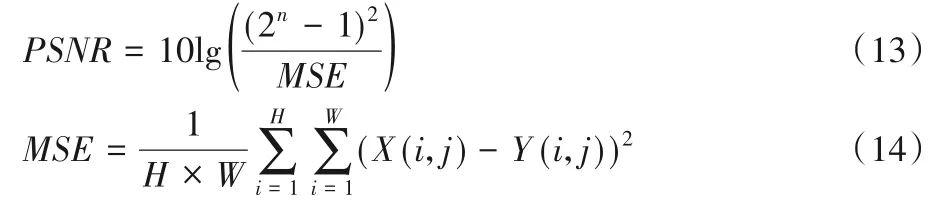
式中:H、W表示图片长宽；X(i，j)、Y(i，j)表示两张图片的像素点；其余均为常数。

3.1 δ=15、δ=25、δ=50下不同算法降噪效果

为了验证本文算法的降噪效果，分别选用BM3D、CSF、DnCNN-B、DnCNN-S、EPLL、TNRD、WNNM 等七种算法进行对比实验，使用的数据集是Set12。通过视觉效果和评价指标PSNR 两个方面来比较各个算法的降噪效果。在噪声水平δ分别为15、25、50 时，数据集中各图片通过降噪后的PSNR 值如表3 所示，最优的PSNR 值已作加粗处理。通过表3 对比可知，在δ=15，25，50 下，本文算法的PSNR 相较原来的DnCNN算法平均提高了1.388 dB、1.725 dB、1.639 dB。文献［30-31］研究表明，降噪水平优于BM3D 达到0.3 dB 的算法是很难实现的，然而本文算法在三个降噪水平上不仅优于BM3D 算法，也优于DnCNN。虽然本文算法在Peppers、Parrot、Starfish三张图片上PSNR值小于DnCNN算法，但就整个数据集而言，本文算法的降噪水平还是优于DnCNN。δ=15时不同算法降噪效果如图11所示。

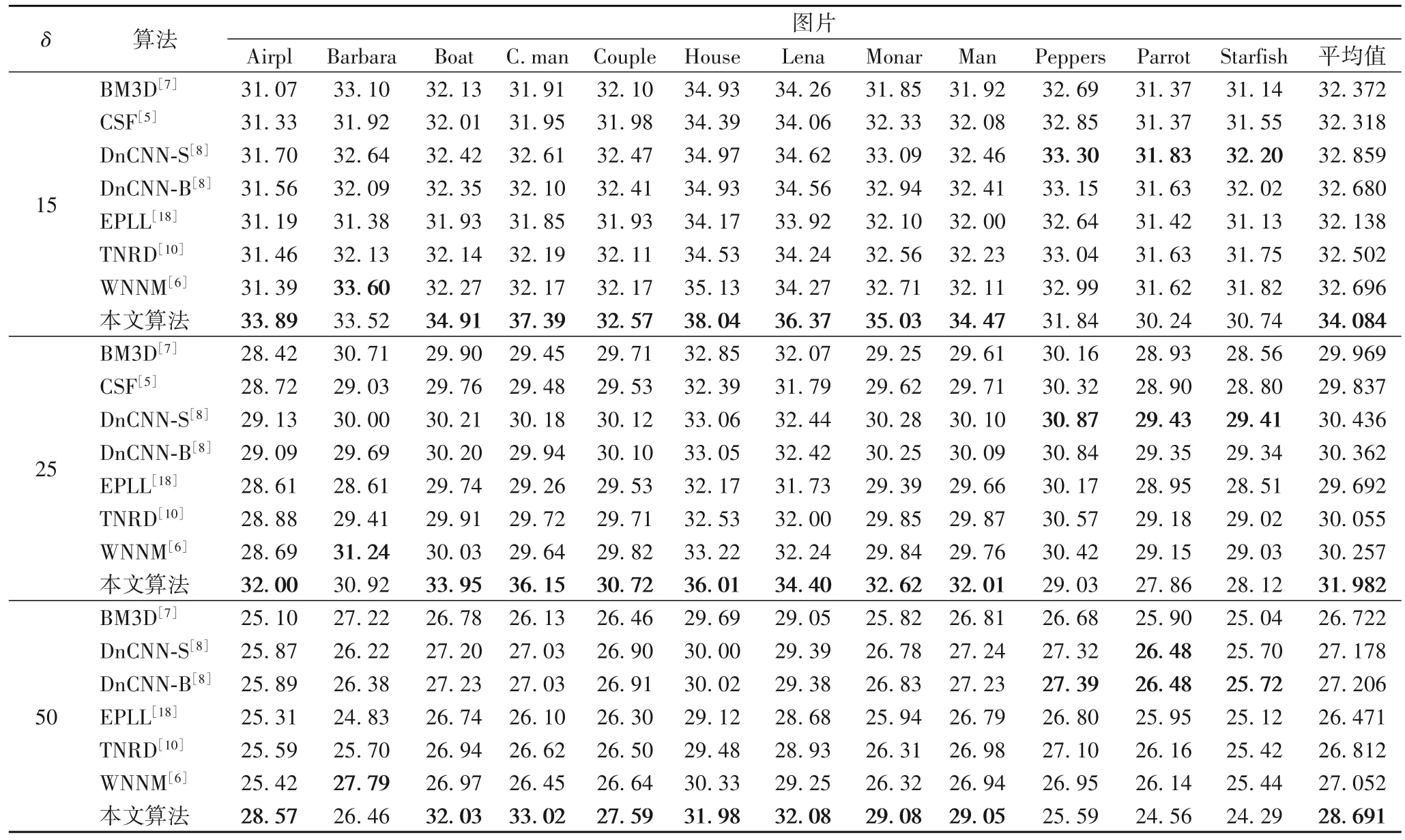
表3 δ=15，25，50时不同算法的PSNR 单位：dBTab.3 PSNR of different algorithms when δ=15，25，50 unit:dB

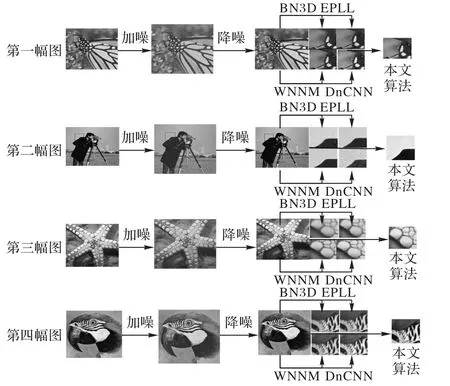
图11 δ=15时不同算法降噪效果Fig.11 Denoising effects of different algorithms when δ=15

由图11 可以明显看出，BM3D 和DnCNN 算法在第一幅和第二幅图像上出现明显的模糊；WNNM 在边缘区域会出现明显的块状，这一点在第二幅图片上较为明显。综上，用于对比的四种算法在边缘细节处理上都有明显的模糊，而本文算法在边缘特征和纹理上相较对比算法都有所改善。本文对比的数据参考了文献［8］中的实验结果。

3.2 盲降噪模型的构成和评估

为得到盲降噪模型，本文训练了δ=15，25，50 等三个模型。不同模型下的降噪效果如图12 所示，随着噪声水平的增加，模型的降噪效果递减，在较低噪声水平下模型的降噪效果明显，且在δ=50 时PSNR 值稳定在30 dB 左右。基于上述实验结果，本文将三个单一水平降噪模型并连成一个盲降噪模型，加噪图片输入模型后由三个子模型并行处理，然后比较各个子模型输出的图像衡量指标EAV 值［32］，最终取其最大值所对应的降噪图像为模型输出，盲降噪模型结构如图13 所示，图中为边缘法向的灰度变化率，M×N表示图片大小。为进一步验证本文模型的降噪效果，引入了结构相似性（Structural SIMilarity index，SSIM），计算式如式（15）:

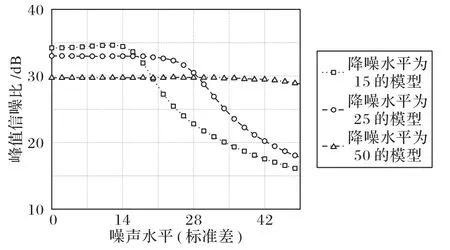
图12 不同模型下的降噪效果Fig.12 Denoising effect under different models

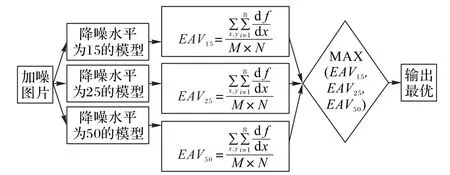
图13 盲降噪模型结构Fig.13 Blind denoising model structure

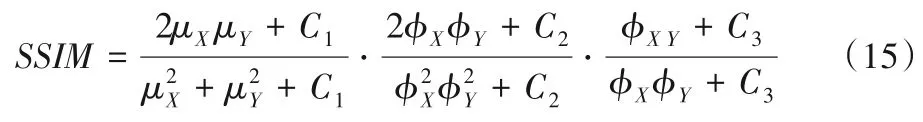
式中:μX、μY，φX、φY及φXY分别表示X、Y的均值、方差及X、Y的协方差；其余均为常数。

SSIM 是一种从亮度、对比度和结构上进行对比的全参考图像质量评价指标，能够准确评估两幅图片纹理和边缘的相似度。在噪声水平分别 为20、30、40、50 下比 较BM3D、WNNM、DnCNN、FFDNET、一致性神经网络（ConSensus neural NETwork，CSNET）这五种算法与本文算法的PSNR 和SSIM值，具体结果如表4 所示。从表4 中不难看出，本文算法在降噪效果上更优，表明本文算法的性能优于目前的其他主流降噪算法，虽然在噪声水平为40 时，本文算法性能略差于FFDNET，但是总体而言本文算法在结构（纹理和边缘）上的降噪效果更明显。

表4 不同算法在Lena图像上的PSNR和SSIM值Tab.4 PSNR and SSIM values of different algorithms on Lena image

不同算法处理图像的用时比较如表5 表示。从表5 中可看出，本文算法的执行时间与文献［8］算法相当。

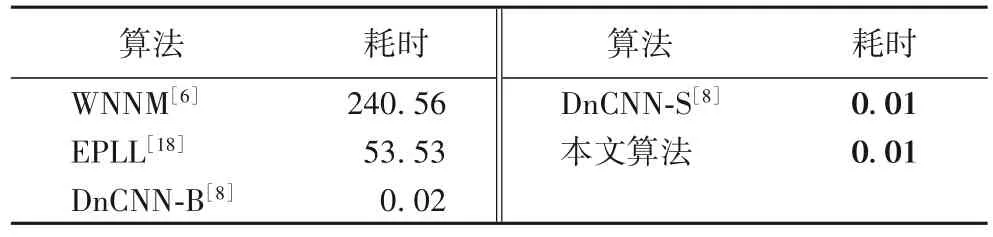
表5 不同算法的执行时间对比 单位：sTab.5 Comparison of execution time of different algorithms unit:s

本文算法对遥感图片的降噪结果如图14 所示，是盲降噪模型对遥感图片在一定噪声水平下的降噪结果。从图14 可以看出，三幅图片的边缘，特别是第一幅河道边缘和第三幅的建筑边缘出现不同程度的模糊，表明本文算法在一些需要超分辨率技术恢复的图像上降噪性能仍有所不足。

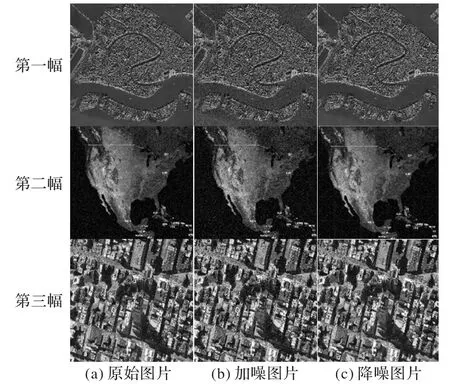
图14 本文算法对遥感图片的降噪结果Fig.14 Denoising results of proposed algorithm on remote sensing images

4 结语

本文将DnCNN、IRBD、GAN 相结合提出了一种新的降噪算法。该算法克服了传统算法计算效率低、单一水平降噪等缺点，改善了图像降噪质量。实验结果表明，本文所提算法的降噪效果相较于DnCNN 模型无论在图片纹理的处理效果还是PSNR 值上都有了较高的提升。此外，本文算法还具有盲降噪和降噪速度快等特点。针对高噪声水平下的图片降噪，本文算法的降噪效果虽然有所提升，但仍有降噪性能不足的问题。下一步研究将继续对本文算法进行改进，将超分辨率技术用于一般图像的降噪，使之在高水平噪声降噪的研究上能取得进一步突破。