基于占优关系的并行程序通信覆盖约减方法

张 辰，田 甜*，杨秀婷，巩敦卫

（1.山东建筑大学计算机科学与技术学院，济南 250101；2.中国矿业大学信息与控制工程学院，江苏徐州 221116）

（∗通信作者电子邮箱tian_tiantian@126.com）

0 引言

消息传递程序具有开发简单、实现便捷、求解高效的特性，是一种应用广泛的并行程序。基于分布式存储架构，消息传递并行程序基于通信语句实现进程之间的交互。通信是消息传递并行程序的主要特征体现，而通信测试的核心是高效生成覆盖通信的测试数据。因此，研究通信覆盖的测试数据生成问题对于消息传递并行程序的测试具有重要意义。

随着程序规模的增大，进程之间的通信愈加频繁，这使得通信测试的难度不断提高。因此，有必要研究有效的通信约减方法，从而降低覆盖难度，提高测试效率。占优关系具有减小问题规模、简化问题求解步骤、提高问题求解效率等优点，已在优化问题的求解中得到了有效应用。鉴于此，本文基于占优关系约减覆盖测试中的目标通信，转换通信约减问题为通信语句约减问题，利用语句占优关系，对通信语句集进行约减。然后，基于约减后的语句，选择相关通信作为覆盖目标，使得覆盖这些目标的测试数据能够覆盖程序的全部通信。

本文的主要工作如下:1）给出通信约减问题的转换理论，将通信约减问题转换为通信语句约减问题；2）基于占优关系约减通信语句集，进而选择目标通信；3）将本文所提出的方法应用到基准程序，并与其他方法进行对比，实验结果验证了本文方法的可行性和高效性。

1 相关工作

不同进程或线程之间的通信始终是研究人员关心的关键问题。Itoh等［1］提出了涉及进程间通信与同步的测试标准，即有序序列准则（Ordered Sequence Criteria，OSC）。Lu等［2］针对并发程序交互空间庞大而难以被彻底搜索的问题，提出具有层次结构的交互覆盖标准，这些标准基于不同的并发故障模型设计。Şerbănuţă 等［3］研究了多线程系统的因果模型，并提出了一种模型检测算法。Vakkalanka 等［4-5］开发了验证工具ISP（In-Situ Partial order），以覆盖每一个有效的线程交互。Siegel 等［6］提出了一个用于消息传递接口（Message-Passing Interface，MPI）并行程序的形式化验证工具TASS（Toolkit for Accurate Scientific Software），使用显式的状态枚举技术来处理由消息传递接口引起的不确定性。此外，Siegel等［7］还提供了一个已被广泛应用的基准并行程序集。Gotovos等［8］提出了Erlang 程序的测试驱动开发方法，并实现了工具Concuerror，以尽早检测并消除执行过程中可能出现的绝大多数与并发相关的错误，该工具探索进程交互并提供发生错误的详细信息。Souza 等［9］关注不同进程的线程之间数据流及其相关通信和同步操作，提出了新的结构测试模型，用以捕获并行和分布式应用程序交互的数据流、控制、通信和同步信息。针对共享内存系统，Huang［10］提出了一种新的无状态模型检测技术MCR（Maximal Causality Reduction），该技术能够系统地探索与给定输入相关的状态空间，并提供最少的执行次数，用以避免冗余的线程交互。Terragni 等［11］提出了一种基于覆盖驱动的测试方法AutoConTest，该方法可以生成有效的并发测试代码，从而实现共享内存访问的交互覆盖。针对程序的并发特性，Nguyen 等［12］利用可参数化的代码转换，生成与原程序相比更简单的程序实例，每个实例捕获原程序交互的简化集，通过并行地检查实例以验证并发程序。Melo 等［13］介绍了共享内存覆盖测试的标准，并给出了测试工具ValiPthread，对测试标准的成本、有效性和强度进行评估。

上述研究主要考虑了进程或线程的交互，但是没有考虑进程间交互覆盖的约减问题。通信是消息传递并行程序进程间交互的主要体现。本文基于消息传递并行程序，研究通信覆盖的约减理论与方法，将通信约减问题转换为通信语句的约减问题，求解通信语句集的约减集，进而选择相关的通信作为覆盖目标，以实现通信覆盖的约减。

作为一种重要的软件测试方法，结构覆盖测试要求生成覆盖程序中某种元素的测试数据，如路径覆盖、语句覆盖以及分支覆盖等。将结构覆盖问题转换为优化问题，并采用进化优化方法求解上述问题，进而生成期望的测试数据，成为目前软件测试领域的重要研究方向之一。

当目标较多时，采用进化优化方法不利于提高覆盖测试的效率。占优关系能够去除冗余目标，简化问题规模，提高测试的效率。针对语句覆盖问题，姚香娟等［14］提出了基于目标语句占优关系的软件可测试性转换理论与方法，利用占优语句代替原有目标语句生成测试数据，以消除标记变量带来的不利影响。为减少弱变异测试中变异体的数量，张功杰等［15］提出了基于统计占优分析的变异体约减方法，该方法利用变异前后的语句构造变异分支，并通过占优关系约减分支集合，得到约减后的变异体，进而提高了变异测试效率。此外，田甜等［16］还将占优关系用于并行程序的死锁检测。本文基于语句占优关系，研究通信覆盖的约减方法，以提高通信覆盖测试数据的生成效率。本文方法将通信约减问题转换为通信语句的约减问题，基于占优关系对通信语句集进行约减，进而选择目标通信，以降低通信覆盖测试数据的生成代价。

2 问题背景

2.1 基本概念

MPI并行程序利用通信函数实现进程间的消息传递。发送函数MPI_Send 和接收函数MPI_Recv 是实现通信的两个基本函数。图1 列出了这两个函数中的常用参数。其中:参数*buf表示数据缓冲区的起始地址；count表示数据个数；datatype表示数据类型；dest表示着数据的接收进程，即目的进程；tag和comm分别表示消息标签和通信域；接收函数中，参数source表示数据的发送进程，即源进程，当source取MPI_ANY_SOURCE 时，该接收函数可接收任意源进程的消息；*status记录数据的接收状态。

定义1通信语句。具有数据发送或接收功能的语句为通信语句，记为n。其中，发送数据的通信语句为发送语句；接收数据的通信语句为接收语句。

定义2通信。若i进程中的一个发送语句ni⁃j发送的数据被k进程中的接收语句nk⁃l所接收，则称ni⁃j与nk⁃l构成通信〈ni⁃j，nk⁃l〉。对于通信〈ni⁃j，nk⁃l〉，若nk⁃l指定了接收数据的源进程，则称ni⁃j与nk⁃l之间的通信为确定通信；若nk⁃l未指定接收数据的源进程，并且能够与多个发送语句通信，则称ni⁃j和nk⁃l之间的通信为不确定通信，nk⁃l为不确定接收语句。

定义3不确定通信组（Ω）。当存在数据源进程为MPI_ANY_SOURCE 且消息标签相同的i(i＞1)条接收语句时，若存在j(j≥i)条发送语句，使得这i条接收语句均能接收这j条发送语句的数据，则称由这些通信语句及其构成的通信组成一个不确定通信组。其中，接收语句即为不确定接收语句，位于接收进程；发送语句位于发送进程。语句间的通信即为不确定通信。

定义4占优。对于i进程中的两个通信语句ni⁃j和ni⁃k，若ni⁃j和ni⁃k构成顺序结构，且ni⁃j位于ni⁃k之前执行，则称ni⁃j占优ni⁃k，记为ni⁃j→ni⁃k。此时，若ni⁃j被执行，则ni⁃k也必然被执行。

定义5占优关系图（D）。D=(V(D)，E(D))，其中，V（D）表示图的顶点集，E（D）表示图的有向边集。令顶点集V(D)=N∪{s，e}，其中，N为通信语句集，s和e分别是进程入口和出口。对任意顶点vj，vk∈V(D)，若vj→vk且vj不被其他顶点占优，则有向边〈vj，vk〉∈E（D）。另外，称vj和vk分别为D的占优顶点和被占优顶点。

定义6约减集。记集合R和N为被测程序的两个语句集，令R⊂N，若以R为覆盖目标生成的测试数据集能够覆盖N，则称R是N的约减集。

2.2 通信图

控制流图是测试人员与学者们分析程序经常使用的一种抽象数据结构。由于本文研究通信的覆盖问题，对于通信语句及通信之间的关系分析是必不可少的工作。因此，本文基于控制流图分析被测程序的通信关系。为了清楚地反映出同一进程中通信语句间的执行关系，以及不同进程中通信语句间的通信，本文以通信语句为顶点进行构图，使用通信图辅助程序分析。

定义7通信图（G）。以程序中的通信语句为顶点，以同一进程中通信语句间的执行关系为有向虚边，以不同进程中通信语句间的通信为有向实边构成的控制流图，称之为通信图。在通信图中，每个进程有各自的入口及出口。

针对位于顺序结构的通信语句，按照通信语句的执行顺序构建其对应的顶点，如图2 所示。图2～4 中，（a）图是位于3种控制结构的通信语句，（b）图的每个顶点分别对应（a）图中的一条通信语句。

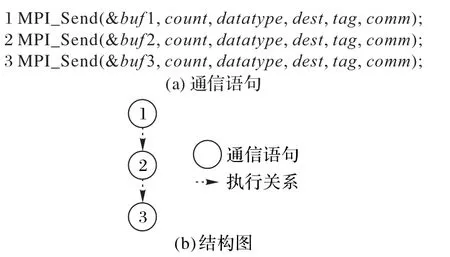
图2 顺序结构Fig.2 Sequence structure

对位于每个分支中的首个通信语句，将其作为分支结构前一个通信语句的分支顶点，分支中的其他通信语句按结构依次构建相应的顶点，如图3所示。

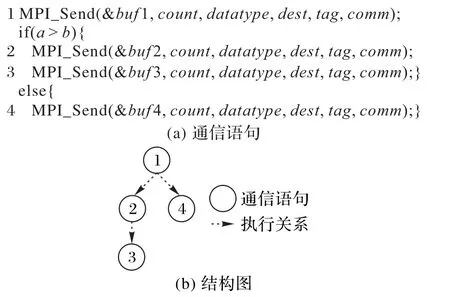
图3 分支结构Fig.3 Branch structure

对于循环结构的通信语句，为了能够清楚并且完整地体现结构特点，借助于辅助顶点，使得循环中通信语句对应的顶点介于两辅助顶点之间，辅助顶点不具备通信功能，如图4所示。

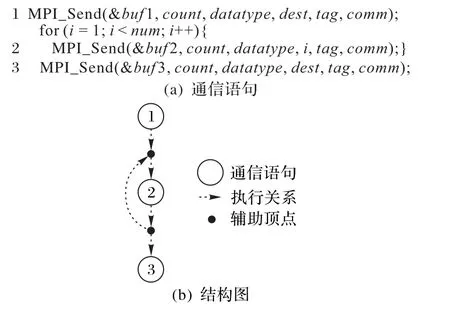
图4 循环结构Fig.4 Loop structure

考虑并行程序S，由num(num＞1)个进程并行执行，分别为S0，S1，‧‧‧，Snum-1，记并行程序S={S0，S1，‧‧‧，Snum-1}。

通信图的构建方法如下:首先，提取各进程中通信语句对应的顶点，并且根据通信语句之间的执行关系构建有向虚边；然后，根据通信语句的参数信息，构建顶点之间的有向实边。由此得到程序对应的通信图。

以图5（a）的示例程序为例，该程序包含5个进程，功能是求取6个数的最大值。

进程S0通过n0-1分别向S1、S2和S3发送2 个数；S1、S2和S3通过n1-1、n2-1和n3-1接收，求取最大值后，通过发送语句n1-2、n2-2、n3-2或n3-3将最大值发送给S0；S0通过n0-2、n0-3和n0-4接收S1、S2和S3发送来的结果后，对前两个数值求取最大值，并将该值与第三个数值通过n0-5或n0-6发给S4；S4通过n4-1接收数值，求取最大值并通过n4-2发送给S0；S0通过n0-7接收数值，最后打印输出。其中，接收语句n0-2，n0-3和n0-4的消息源进程为MPI_ANY_SOURCE，并且消息标签相同。也就是说，n0-2、n0-3和n0-4中的每一条语句都能够接收来自发送语句n1-2、n2-2、n3-2和n3-3的消息，这些通信语句及其构成的不确定通信组成不确定通信组。

示例程序的通信如图5（b）所示。其中，顶点对应图5（a）中的进程入口s、出口e及通信语句，如S1的顶点1 对应n1-1。有向虚边表示通信语句间的执行，以〈n1-1，n1-2〉为例，它表示n1-2在n1-1之后执行。有向实边则对应顶点间的通信，如〈n0-1，n1-1〉表示S0中n0-1发送的数据由S1的n1-1接收。

3 基于占优关系的通信覆盖约减方法

本文重点研究通信覆盖的约减理论与方法，主要思路是:首先，转换通信约减问题为通信语句约减问题；然后，利用通信语句的占优关系，约减通信语句集；最后，基于约减后的通信语句选择通信作为目标通信集。

3.1 通信约减问题的转换

由2.2 节得到的程序通信图，可以清晰地看出通信与通信语句之间的对应关系，基于该对应关系，将通信的约减问题转换为通信语句的约减问题。下面，针对确定通信和不确定通信两种类型分别提出通信约减问题的转换理论。

1）确定通信约减问题的转换。

对于确定通信〈ni-j，nk-l〉而言，当通信〈ni-j，nk-l〉的两个通信语句ni-j、nk-l被覆盖时，通信〈ni-j，nk-l〉产生，即通信〈ni-j，nk-l〉被覆盖。因此，通信的产生与这两个通信语句的覆盖具有一致性，可以通过这两个通信语句的覆盖判定通信的覆盖，从而通过约减通信语句实现通信的约减。也就是说，将确定通信的约减问题转换为通信语句的约减问题。例如，在图5 示例程序中，当确定通信〈n0-1，n1-1〉的两个通信语句n0-1和n1-1被覆盖时，该通信即被覆盖；当所有确定通信相关的通信语句被覆盖时，所有的确定通信即被覆盖。

2）不确定通信约减问题的转换。

在不确定通信组中，一个发送语句可以与多个接收语句通信，同样地，一个不确定接收语句可以与多个发送语句通信。因此，当不确定通信〈ni-j，nk-l〉的两个通信语句ni-j和nk-l被覆盖时，不能判定〈ni-j，nk-l〉被覆盖。如图5 示例程序中，n1-2可与n0-2、n0-3和n0-4通信，n0-2可与n1-2、n2-2和n3-2或n3-3通信，当n1-2和n0-2被覆盖时，不能判定〈n1-2，n0-2〉被覆盖。影响不确定通信〈ni-j，nk-l〉覆盖的因素为程序输入及调度序列。调度序列指进程的执行顺序。当进程调度遵循影响〈ni-j，nk-l〉覆盖的调度序列时，若通信语句ni-j和nk-l被覆盖，则不确定通信〈ni-j，nk-l〉被覆盖。例如示例程序中，当调度序列为S1S2S3时，若n0-2与n1-2被覆盖，则不确定通信〈n1-2，n0-2〉被覆盖。由此，将不确定通信的约减问题转换为通信语句的约减问题。

进程遵循某一调度序列时，将影响不确定通信组中多个通信的覆盖。当不同调度序列在某一位置上的进程相同时，相同的通信被覆盖。例如图5 示例程序的调度序列:S1S2S3和S1S3S2，进程S1的调度相同，所以，两个序列均覆盖通信〈n1-2，n0-2〉。受此启发，本文通过算法1实现调度序列的约减。在算法1 中，遍历通信语句，若该语句为不确定接收语句，则其属于一个不确定通信组。将发送进程的进程编号按照大小排序并变换，得到该通信组的目标调度序列集。考虑所有不确定通信组，得到整个被测程序S的目标调度序列集。

算法1 目标调度序列集生成。

输入 被测程序S；

输出S的目标调度序列集Δ。

3.2 目标通信的选择

将通信的覆盖问题转换为通信语句的覆盖问题后，本节给出通信语句集的约减方法，基于约减后的通信语句，得到目标通信集。基于通信语句的占优关系，构造占优关系图。由占优定义可知，当占优顶点被执行时，被占优顶点也将被执行。因此，占优关系图的占优顶点组成了通信语句集的约减集，以占优顶点为发送或接收语句的通信即为目标通信。当目标通信被覆盖时，以被占优顶点为发送或接收语句的通信也将被覆盖。基于占优关系的通信约减算法如算法2所示。

算法2 基于占优关系的通信约减。

输入 被测程序S；

输出 目标通信集Φ={Φ0，Φ1，‧‧‧，Φnum-1}。

3.3 实例分析

下面以图5 中的示例程序为例，说明通过算法1 和算法2得到示例程序的目标调度序列集和目标通信集的过程。

基于算法1，在进程S0中，n0-1是发送语句，因而继续遍历n0-2。根据通信图可知，n0-2为不确定接收语句。分析可得n0-2所在Ω0的发送进程数及进程编号，分别为3 和（1，2，3），并且进程编号按照大小排序得到ψ0=S1S2S3，ψ0加入Ψ0。将ψ0首位进程移至最后得到ψ1=S2S3S1，ψ1加入Ψ0，同理可得ψ2=S3S1S2，并添加到Ψ0，至此调度序列变换结束。将Ψ0加入到Δ，并且不再遍历n0-3和n0-4。由于n0-5、n0-6和n0-7不是不确定接收语句，因而S0遍历结束。同理遍历其他进程中的通信语句。最终可得，目标调度序列集Δ=｛S1S2S3，S2S3S1，S3S1S2｝。

示例程序的5 个进程S0、S1、S2、S3和S4，对应5 个通信语句集N0=｛n0-1，n0-2，n0-3，n0-4，n0-5，n0-6，n0-7｝、N1=｛n1-1，n1-2｝、N2=｛n2-1，n2-2｝、N3=｛n3-1，n3-2，n3-3｝和N4=｛n4-1，n4-2｝。

下面通过算法2，根据占优关系得到示例程序的目标通信集。借助于图5（b）通信图，首先，分析S0。以s为占优顶点构造D0。关于n0-1，由通信图可知，n0-1与s构成顺序结构，所以将n0-1作为D0的被占优顶点。同样地，n0-2，n0-3和n0-4为D0的被占优顶点。对于n0-5，由于不被s占优，所以构造占优顶点为n0-5的D1，并将n0-5添加到N0，将与n0-5相关的通信并入S0目标通信集Φ0。类似地，构造以n0-6为占优顶点的D2。关于n0-7，则作为D0的被占优顶点。至此，S0包含的占优关系图（图6）构造结束。R0=｛n0-5，n0-6｝，Φ0=｛〈n0-5，n4-1〉，〈n0-6，n4-1〉｝。

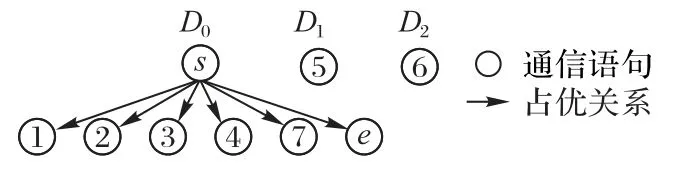
图6 S0的占优关系图Fig.6 Dominant relation diagram of S0

类似地，可以得到S1、S2和S4的占优关系图，如图7 所示。对应地，约减集R1=∅，R2=∅，R4=∅。目标通信集Φ1=∅，Φ2=∅，Φ4=∅。S3的占优关系图如图8 所示，R3=｛n3-2，n3-3｝，Φ3=｛〈n3-2，n0-2〉，〈n3-2，n0-3〉，〈n3-2，n0-4〉，〈n3-3，n0-2〉，〈n3-3，n0-3〉，〈n3-3，n0-4〉｝。程序S的约减集R=R0∪R1∪R2∪R3∪R4=｛n0-5，n0-6，n3-2，n3-3｝。基于R中的通信语句得到目标通信集Φ=｛〈n0-5，n4-1〉，〈n0-6，n4-1〉，〈n3-2，n0-2〉，〈n3-2，n0-3〉，〈n3-2，n0-4〉，〈n3-3，n0-2〉，〈n3-3，n0-3〉，〈n3-3，n0-4〉｝。

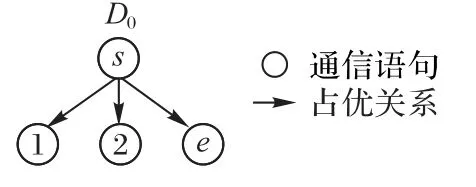
图7 S1、S2、S4的占优关系图Fig.7 Dominant relation diagram of S1，S2 and S4

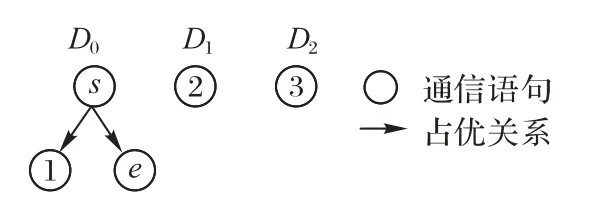
图8 S3的占优关系图Fig.8 Dominant relation diagram of S3

上述分析可得到示例程序的目标调度序列集和目标通信集，能够初步表明本文方法的可行性。下面通过实验进一步验证本文方法的有效性。

4 实验与结果分析

4.1 验证问题

通过回答如下问题，验证本文所提方法的性能:

1）以本文所提方法得到的通信作为覆盖目标，生成的测试数据能否覆盖全部通信？

2）采用本文所提方法，能否提高通信覆盖测试数据生成效率？

为验证问题1），将本文方法生成的测试数据作为输入，运行被测程序，通过通信的覆盖情况回答本文方法的可行性。

为验证问题2），记以全部通信作为覆盖目标的测试数据生成方法为方法A；将随机选择目标通信的测试数据生成方法记为方法B；此外，将随机选择调度序列的测试数据生成方法记为方法C。比较本文方法与方法A、B 和C 的通信覆盖率、成功率及测试时间，验证本文方法的高效性。

4.2 实验设计

结合验证问题，选取以下7 个基准并行程序作为被测程序，这些程序的基本信息如表1 所示。其中:Max 为图5 示例程序，用于求取多个输入值的最大值；Min 用于求取多个输入值的最小值；Triangle 用于判断输入值中最大的3 个值能否构成三角形及所构成三角形的类型；Search 用于字符检索；Adder_par 用于对多个输入值的求和运算，Matmat_mw 用于两矩阵相乘运算，这两个程序均选自FEVS 基准并行程序测试集［7］；IS_Mode 对输入值进行排序并统计众数，该程序来自于基准测试程序集NPB（NAS Parallel Benchmarks）［17］。这些被测程序具有不同的功能、属性和测试难度，能够用来有效评价不同的通信覆盖方法。

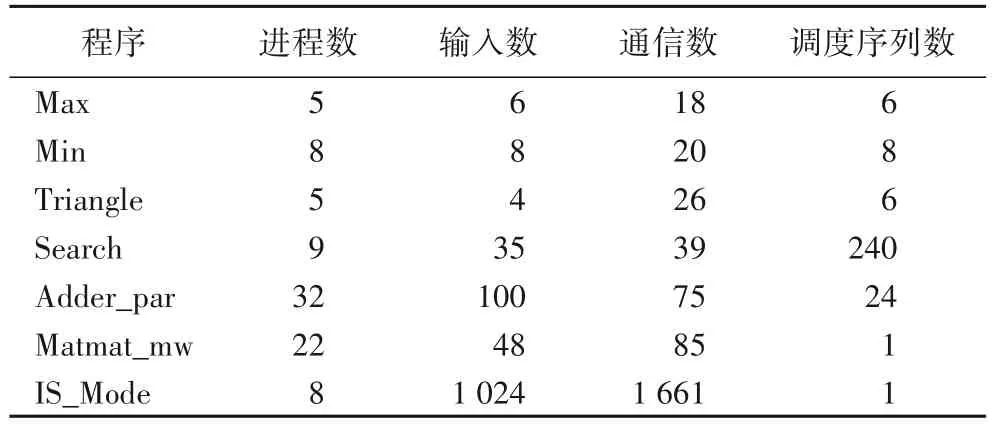
表1 实验程序的基本信息Tab.1 Basic information of experimental programs

采用本文方法对被测程序的通信实施约减。为了直观地反映出通信的约减效果，分别计算各程序通信的减少比RA，计算式如下:

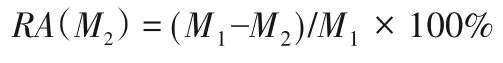
其中，M1、M2分别表示全部通信集的大小和目标通信集的大小。

为了提高被测程序的覆盖率，已有许多研究者提出了不同的测试数据生成技术，其中，遗传算法的应用最为广泛［18］。本文方法与方法A、B和C均采用遗传算法生成测试数据。遗传算法的相关参数设置如下:最高迭代次数为500，种群规模为30，选择操作为轮盘赌，单点交叉概率和单点变异概率分别为0.9 和0.3［19］。遗传算法的个体包括被测程序的输入数据和调度序列两部分，采用二进制编码方式，通过分支距离［14］计算个体适应值。

4.3 实验过程

实验环境配置如下:硬件为Intel Core i5 处理器、500 GB硬盘和8 GB 内存；软件采用Windows 10 操作系统、Visual Studio 2017 编译器，以及消息传递接口标准工具Microsoft MPI v9.0.1。

实施本文方法时，首先，根据3.1 节提出的不确定通信处理策略（算法1），求解目标调度序列集Δ。然后，结合通信图，依据通信约减算法（算法2），约减被测程序的通信语句集，基于此，得到目标通信集Φ。接着，基于目标通信集Φ及目标调度序列集Δ，运用遗传算法生成测试数据。最后，将生成的测试数据作为输入运行被测程序，判断生成的测试数据是否覆盖全部通信。

借由通信图分析不确定通信组，得到全部调度序列集。在方法A中，以全部调度序列作为目标调度序列集，依次覆盖全部通信，用以验证本文方法的高效性。为了保证实验对比的公平性。在方法B 中，其目标调度序列集Δ与本文方法相同，并且其目标通信集的数量与本文方法也相同，用以验证本文通信约减策略的重要性。在方法C 中，其目标通信集Δ与本文方法相同，每次实验以全部调度序列作为目标调度序列集，用以验证本文约减调度序列策略的必要性。针对方法A、B和C，基于各自的目标通信集Φ和目标调度序列集Δ分别运行遗传算法生成测试数据。

考虑到遗传算法的随机性，每一方法均运行10 次，记录每次实验的通信覆盖率及测试时间，并将各项记录的平均值作为该测试方法的最终实验结果。需要说明的是，一次实验中若全部通信均被覆盖，则视该次实验为成功，成功率值指实验成功的次数占总实验次数的比值。

4.4 结果分析

采用本文方法对被测程序的通信、调度序列进行约减，得到目标通信集和调度序列集，如表2 所示。由表2 可以得出，相较被测程序的全部通信，本文方法选择的目标通信数量较少，目标通信减少比为55.6%～99.6%，其中，Min、Triangle、Search、Adder_par、Matmat_mw和IS_Mode的通信减少比较高，而Max 的通信减少比相对较低，这是因为Max 的部分非被占优通信语句位于不确定通信组，而不确定通信组中的每一通信语句都与多条通信相关，因此，依据算法2 得到的目标通信数较多，使得减少比相对较低。

表2 实验程序的约减情况Tab.2 Reduction situation of experimental programs

本文方法的目标通信集、全部通信集以及对比方法全部通信集的平均覆盖率如表3 所示。基于每次实验的通信覆盖率，得到所有测试方法的成功率，如表4 所示。表5 是不同方法的测试时间对比。

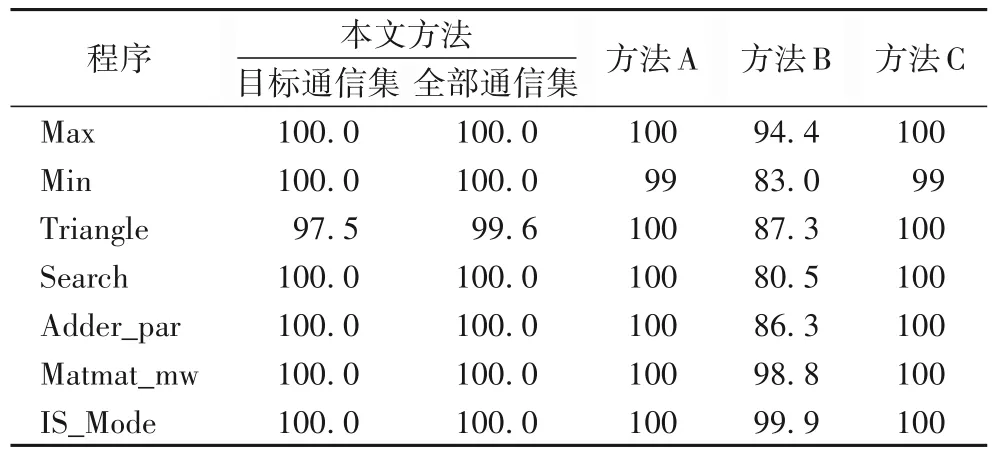
表3 不同方法的通信覆盖率比较 单位：%Tab.3 Comparison of communication coverage ratio among different methods unit:%

表4 不同方法的成功率比较 单位：%Tab.4 Comparison of success rate among different methods unit:%

表5 不同方法的测试时间比较 单位：msTab.5 Comparison of testing time among different methods unit:ms

回答问题1）由表3 可知，当被测程序目标通信覆盖率为100%时，全部通信覆盖率同为100%。这表明以本文所提方法得到的通信作为覆盖目标，生成的测试数据能够覆盖全部通信，验证了本文方法的可行性。此外，对于Triangle程序，由于在第3 次实验中，有一条目标通信没有被覆盖，导致当次实验的目标通信及全部通信覆盖率分别为75%和96.2%，其余9 次实验的目标通信及全部通信覆盖率均为100%，因此，平均目标通信覆盖率和全部通信覆盖率分别为97.5%和99.6%。

回答问题2）首先，对比本文方法与方法A。通过表3～4能够看出，两者均具有较高的通信覆盖率和成功率，但是，表5 结果表明，本文方法的测试时间明显少于方法A 的测试时间。因此，相较于方法A而言，本文方法能够在不降低通信覆盖率的前提下，减少的测试数据的生成时间最高达95%。

然后，对比本文方法与方法B。由表3～4 可知，本文方法的通信覆盖率和成功率均高于方法B。这是因为本文方法基于占优关系选取目标通信，以此生成的测试数据能够覆盖全部分支通信，而方法B不能。因此，本文方法有效地提高了通信覆盖率。表5 结果表明，相较方法B，本文方法在程序Min、Search、Adder_par、Matmat_mw和IS_Mode的测试时间较多，原因是，所选目标通信包含覆盖难度较大的通信，测试数据生成难度较高，因此时间消耗较多。但是正如前文所述，所生成的测试数据对全部通信的覆盖率较高。

接着，对比本文方法与方法C。由表3～4 可知，方法C 取得了较高的通信覆盖率和成功率。通过表5 进一步分析发现，相较于方法C，本文方法的时间消耗普遍少于方法C。但本文方法在Adder_par 的时间消耗多于方法C。可能的原因是，本文方法所选目标调度序列集的性能不高。

综上所述，采用本文方法，通过占优关系得到合理的目标通信，并在部分调度序列下，基于遗传算法生成覆盖目标通信的测试数据，能够在保证通信覆盖率的前提下，减少测试数据生成时间，提高测试效率。

5 结语

本文研究了并行程序通信覆盖的约减理论与方法。首先，将通信约减问题转换为通信语句约减问题。然后，利用占优关系对通信语句进行约减，基于约减后的通信语句得到目标通信，使得以这些通信为覆盖目标生成的测试数据能够覆盖全部通信。通过设定调度序列集，消除不确定通信对于通信覆盖的影响；基于对通信语句的占优关系分析，减少目标通信的数量。实验结果表明，以本文方法选择的通信作为覆盖目标，生成的测试数据能够覆盖被测程序的全部通信；本文方法能够达到较高的通信覆盖率，并减少了测试数据的生成时间。

值得说明的是，当前工作基于静态分析实现通信的约减。因此，开发基于本文方法的原型系统，实现基于占优关系的通信覆盖自动化约减是我们的后续研究工作。同时，本文没有考虑调度序列性能，可以融合调度序列的性能评价，选择性能优异的目标调度序列集，以便进一步提高通信覆盖的效率。此外，在通信覆盖方面，本文基于单目标覆盖的方式实现通信覆盖的测试数据进化生成，实现面向多目标覆盖的测试数据生成也是下一步要研究的课题。