参数独立的加权局部均值伪近邻分类算法
蔡瑞光,张德生,肖燕婷
(西安理工大学理学院,西安 710054)
(∗通信作者电子邮箱2151577901@qq.com)
0 引言
数据挖掘[1]是在大型数据存储中自动发现有用信息的过程,分类属于数据挖掘的四大任务之一。分类器能够把数据集中的测试样本映射到特定类别的分类函数或分类模型,已被广泛应用于文字以及人脸识别、医学、文本分类、商务、图像处理、自然语言理解、垃圾邮件识别等领域。
局部均值K近邻(Local Mean-basedK-Nearest Neighbor,LMKNN)算法是文献[2]提出的一种经典的分类算法,其核心思想是先找到待分类样本在训练集中每类样本中的k个近邻的局部均值点,再将测试样本分到离它最近的局部均值点所属的类别。伪近邻(Pseudo Nearest Neighbor rule for pattern classification,PNN)算法是文献[3]提出的一种用伪最近邻代替真正最近邻的分类算法,首先找到待测样本在每类训练样本中的伪最近邻,再将其分到距离测试样本最近的伪最近邻所属于的类。局部均值伪最近邻(Local Mean-based Pseudo Nearest Neighbor,LMPNN)算法[4]是将经典的局部均值K近邻(LMKNN)算法和伪最近邻(PNN)算法相结合,充分利用了样本的局部信息,降低了离群点对分类结果的影响。该算法的主要特点是简单、快速且易于实现,至今仍被广泛地应用。但该算法也有明显的不足之处,参数的设置具有主观敏感性,分类结果受k值的影响较大;将每个属性值和类别均同等对待,忽略了每个属性值和类别对分类结果的不同程度的影响。因此,确定最佳k值和属性权重成为众多学者的研究方向。
针对LMPNN 算法存在的不足之处,文献[5]提出了基于局部均值与类均值的近邻分类算法,该算法利用测试样本对每个训练类中k个近邻的局部均值的信息和整体均值的信息进行预测分类。文献[6]提出了基于局部均值表示的K近邻分 类(Local Mean Representation-basedK-Nearest Neighbor classification,LMRKNN)算法,该算法首先寻找每个测试样本在每类中的k个近邻并用k个近邻计算k个局部均值;其次,使用每类的k个局部均值线性表示测试样本;最后,计算基于表示的距离作为测试样本的分类决策函数。文献[7]提出了基于加权均值表示的K近邻分类(Weighted Local Mean Representation-basedK-Nearest Neighbor classification,WLMRKNN)算法,该算法充分利用k个近邻的局部信息,并且赋予由k个近邻计算的多局部均值不同的自适应权重表示测试样本,且WLMRKNN 是对LMRKNN 分类器权重的扩展。文献[8]提出了基于局部均值表示的调和近邻分类(K-Harmonic Nearest Neighbor classification based on Local Mean Representation,LMRKHNN)算法,该算法计算测试样本与每一个局部均值之间的距离,并用这些距离计算调和距离作为分类测试样本的决策函数。文献[9]提出了基于稀疏系数和残差的k近邻加权分类算法,该算法分别利用稀疏系数和残差对距离度量进行加权,来充分考虑样本的空间分布和属性之间的相关程度。
上述几种改进算法虽然都具有较好的分类效果,但是仍然存在k值设置困难和类别权重仍然敏感的问题,本文将基于成功历史记录的自适应参数差分进化(Success-History based parameter Adaptation for Differential Evolution,SHADE)算法与LMPNN算法结合用于解决数据分类问题,提出参数独立的加权局部均值伪近邻分类(Parameter Independent Weighted Local Mean-based Pseudo Nearest Neighbor classification,PIW-LMPNN)算法。PIW-LMPNN 并未将特定类别的最优权重和最优值作为两个独立的问题,而是采用一种新颖的实值编码方案——SHADE 算法将两个优化问题共轭为一个单目标连续非凸优化问题去解决。将新的分类算法在 15 个 UCI(UC Irvine machine learning)以 及 KEEL(Knowledge Extraction based on Evolutionary Learning)数据集上进行测试,实验仿真结果表明,将SHADE 算法与LMPNN 算法结合能有效解决分类问题,其算法的稳定性以及求解精度得到了明显的提升。
1 LMPNN算法
在特征空间Rd中,假定训练集T=有L个类标号ω1,ω2,…,ωL,并且是训练集中类别为ωj的训练样本集合。N和Nj分别代表训练集T中样本的个数和类别为ωj的训练集中样本的个数。算法步骤如下:
步骤1 计算待测试样本x到中样本的欧氏距离:

步骤2 将类别ωj中的欧氏距离按升序排列,并取前k个近邻
步骤3 计算待测试样本x在类别ωj中前i个近邻的局部均值向量:

步骤4 给每一类中的局部均值向量分配不同的权重。在ωj类中,第i个局部均值向量的权值为:

步骤5 计算每类ωj中的伪近邻。
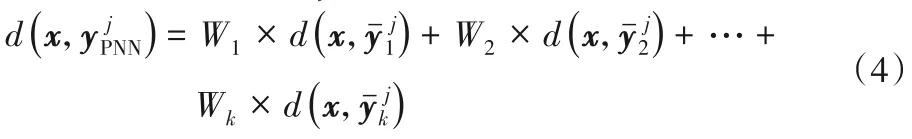
步骤6 预测待测样本x的类标号c。

例1 图1中,是一个三类二维分类问题。测试样本来自于第1 类样本集。在表1 中,当k=2,3,4 时,首先使用LMPNN分类器,测试实例在k为2 和4 时被误分为第2 类,在k为3 时被正确分类。其次,在使用LMPNN 分类器之前,使用一组关于类别的特定权重时(如式(6)所示),测试实例均被正确分为第1 类。所以,LMPNN 分类器的性能依赖于预先设置的k值和属性权重。

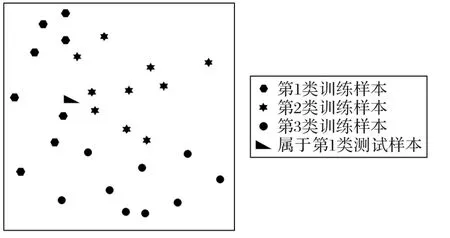
图1 测试样本与训练样本Fig.1 Test samples and training samples
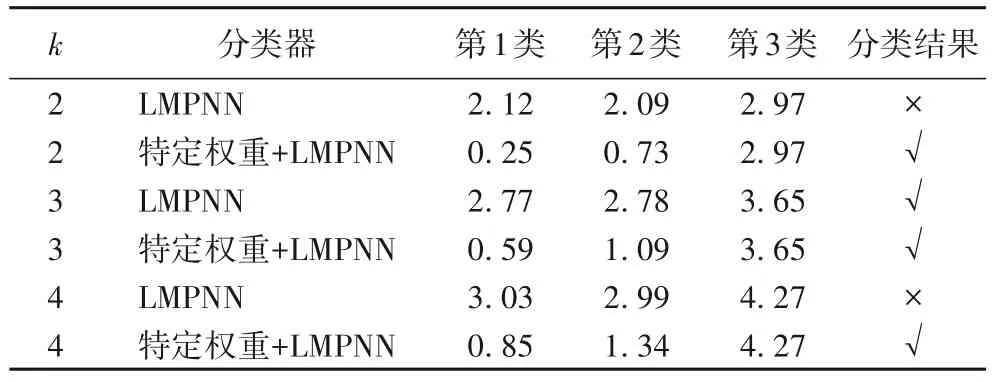
表1 不同k值下的伪近邻分类Tab.1 Pseudo neighbor classification under different k values
2 SHADE算法
差分进化(Differential Evolution,DE)算法[10]是一种基于种群的全局搜索算法,许多实际问题利用DE 已得到有效解决。由于其算法结构简单易于执行、控制参数少且有较强的搜索能力,差分进化算法吸引了众多学者的关注和研究。但是该算法的性能在很大程度上依赖于缩放比例因子F和交叉概率CR等参数的选择。SHADE 算法[11]是DE 的最新变体,该算法是利用自适应技术智能地计算F和CR的最优值,在一定程度上弥补了DE算法的不足。
SHADE 是一种基于群智能的随机优化算法,具有种群内信息共享以及记忆个体最优解的优点,即通过种群内个体间的竞争与合作来实现对优化问题的求解,其本质是一种基于实值编码的贪婪遗传算法[12]。首先随机初始化种群Y0=[y1,0,y2,0,…,yN,0],N为种群规模。其 中,个 体yi,0=[yi,1,0,yi,2,0,…,yi,d,0]用于表示特征问题解,d为优化问题的维数。算法的基本思想为:对当前的种群进行变异和交叉操作后,产生一个新的种群,其次运用贪婪的思想对两个种群进行选择,产生新的一代种群。具体而言,首先通过式(7)对每一个个体yi,g实施变异操作,得到与其相对应的变异个体,即:
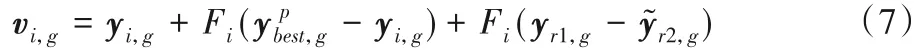
在变异策略DE/current-to-pbest/1 中,把被淘汰的个体存储在一个集合A中,P表示当代种群组成的集合。表 示随机从当代种群中适应度靠前的N×p(p∈[0,1])个个体中选择一个;yi,g和yr1,g是从集合P中随机选择的两个个体是从种群和A合并后的集合中随机选择的一个个体;Fi为收缩因子。其次,利用式(8)对y i,g和变异个体vi,g实施交叉操作,生成个体ui,g,即:
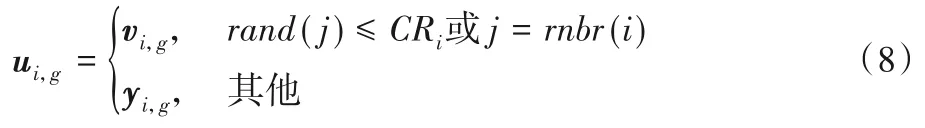
其中:rand(j)为[0,1]的随机数;CRi为[0,1]的交叉因子;rnbr(i)为{1,2,…,d}的随机变量。最后,运用贪婪思想对个体进行选择,如式(9)所示,在个体ui,g和个体y i,g中保留较优个体进入下一代迭代。

其中f为适应度函数。
交叉因子CRi和收缩因子Fi的计算式如下:
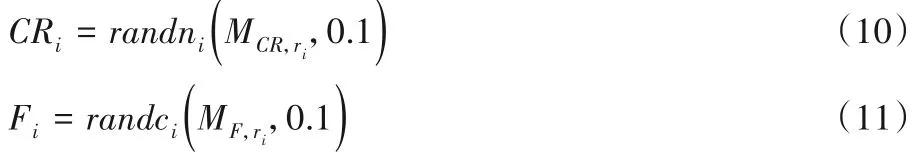
其中:randci(α,β)和randni(α,β)分别服从柯西分布和正态分布;(i=1,2,…,H)的初始值均为0.5,ri∈[1,H]。根据式(12)~(13)进行更新:
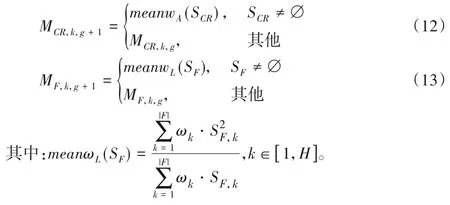
将每一代SCR和SF的平均值都存储在历史矩阵MCR和MF中,并且保留了一组参数H,随着搜索的进行来指导控制参数的自适应。因此,即使某个特定的SCR和SF中包含一组较差的值,也无法直接负面地影响已存储在存储器中的参数。此外,SHADE 算法使用较少的迭代次数相较经典DE 算法产生了更好的结果,保留了全局搜索策略,并通过基于差分形式的变异操作和基于概率选择的交叉操作引导种群进化。
3 参数独立的加权局部均值伪近邻分类算法
通过对LMPNN 的描述可知,该分类器对k值选择仍然敏感,且对所有实例都使用一组相同的权重,均等地对待每一类中的每一个属性,并未考虑每类中代表性属性的影响,且忽略了利用有用的信息来区分特定的类别。为此,提出了参数独立的加权局部均值伪近邻分类(PIW-LMPNN)算法,无需人为设定参数,可得到一组与类相关的最佳权重集,并同时通过优化得到最优k值。其基本思想为:对每类中的样本施加特定类的属性权重,引入了基于类的属性加权方法,通过SHADE为每个类找到一组最佳权重,使每类代表性的属性权重达到最高,同时将冗余的、嘈杂的属性的权重降到最低;SHADE 同时可以经过优化得到最优k值;最后运用LMPNN 分类器预测测试样本的类别。
3.1 目标函数
引入目标函数(14),通过SHADE 算法使其最小化,得到的参数值可以有效提高LMPNN算法的性能。
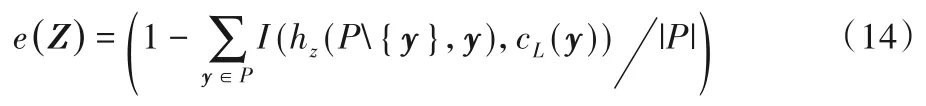
其中I是一个指示函数,如式(15)所示:
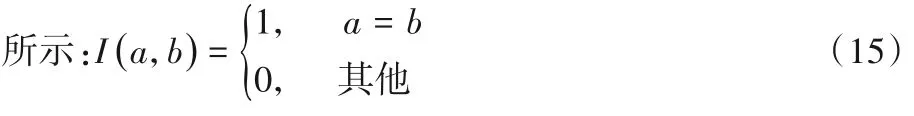
目标函数的域应与分类器的参数空间的域相关,表示为Z∈RD。h(·)是LMPNN 算法中的相异度度量。此外,z∈Z是e(·)的候选解,可以从中解出参数k和w的最佳选择。接下来的任务是对z进行编码,由SHADE 进行演化的同时计算得到k和w。z为D维向量,其中D=(L×d)+1,水平连接w的每一行并为k添加一个额外的单元格(如图2 所示)。虽然能够对w和k进行同时编码,但是z的这种表示形式不能直接用于实践中的优化,因为w是一个实值矩阵,其每一行的取值都应在0~1 的范围内。另一方面,k值是一个在1~的范围内的整数。在更新之后,通过从演化解z中提取w和k可以解决此问题。
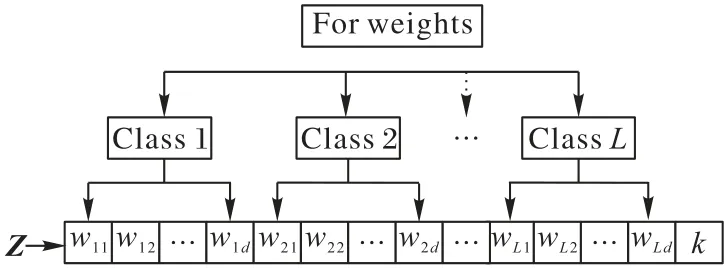
图2 通过SHADE算法优化后的最佳权重和k值Fig.2 Optimal weights and k value after optimization of SHADE algorithm
3.2 本文算法
所提出的PIW-LMPNN 分类器首先初始化N个解Z,其中(0 ≤z(f)≤1,∀z∈Zandf=1,2,…,D),接下来对每一个参数进行更新,在提取相应的w和k后,通过计算e(·)进行评估。对于w,更新和提取可以通过对每个权重集[z(rd-d+1),z(rd-d+2),…,z(rd)]进行归一化来完成,取值范围为0~1。对于k,z(D)的取值范围在ε~1,其中ε是一个非常小的正实数(对于z(D)≤0,取z( D)=ε;对于z(D)≥1,取z(D)=1;否则z(D)的取值保持不变)。如式(16)所示,修改后的z(D)乘以k的最大允许值并四舍五入到下一个整数。

种群通过SHADE 算法进行更新。在SHADE 的每次迭代中,通过进化生成新的解,找出当前种群中使目标函数最小化时对应的w和k。将获得的参数与训练集T一起使用,计算LMPNN 的分类误差,当其误差小于相应父代的误差时,新解决方案才成为总体的一部分。最后将所得的全局最优的w和k用于对测试样本进行分类。具体算法描述如算法1所示。
算法1 PIW-LMPNN算法。
输入 训练集T,测试样本x,H=100;
输出 测试样本x的类别c。
步骤1 在[0,1]随机初始化种群Z=[ztj]N×D;
步骤2 利用SHADE 算法优化目标函数e(·),找出最优的w*和k*;
步骤3 使用w*和k*以及式(17)去寻找测试样本x在每类中的近邻集合
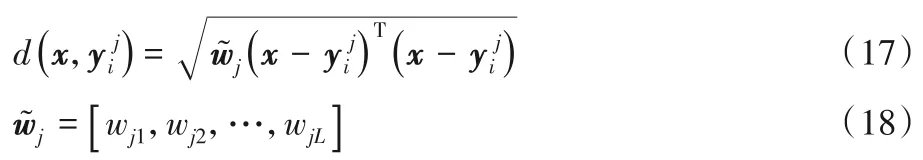
步骤4 通过式(2)计算得到测试样本x在每类中局部均值的集合
步骤5 通过式(3)~(4)计算测试样本x在每类中的伪近邻,以及测试样本到伪近邻的距离
步骤6 通过式(5)预测测试样本x的类别c。
4 实验与结果分析
为了验证PIW-LMPNN 算法的分类性能,本文选取15 个常用数据集进行仿真实验。其中,数据集包含数据量为150~2 536,特征维数为4~73,类别数为2~11。表2 给出了二分类问题的混淆矩阵。其中:TP(True Positive)表示将正类预测为正类数;TN(True Negative)表示将负类预测为负类数;FP(False Positive)表示将负类数预测为正类数;FN(False Negative)表示将正类数预测为负类数。表3 给出了本文实验数据的部分信息。

表2 分类结果混淆矩阵Tab.2 Confusion matrix of classification results

表3 数据集详细信息Tab.3 Detailed information of datasets
4.1 评价指标和非参数检验
以分类准确率、综合评价指标以及非参数检验——Wilcoxon 符号秩检验、Friedman 秩方差检验以及Hollander-Wolfe两处理等作为评价指标比较PIW-LMPNN和其他分类算法的性能。
4.1.1 分类准确率
分类准确率(Acc)的计算式如下:

TP和TN的值越大表明分类正确的样本数越多,则分类准确率越高[13]。
4.1.2 综合评价指标
综合评价指标(F-Measure)是精确率(Precision,P)和召回率(Recall,R)的加权调和平均,如式(20)所示。

其中:P是指正确判别为该类的样本数与分类器实际判别属于该类的样本总数的比值,如式(21)所示;R是指正确判别为该类的样本数与原样本集中实际属于该类的样本总数的比值,如式(22)所示。

当a=1时,F1=。F1是一种综合考虑P与R的评价指标,具有较好的独立性、时间无关性、可扩展性和较低的计算复杂度。当F1的值越大时,表示分类器越有效。
4.1.3 Wilcoxon符号秩检验
两配对样本分布差异的非参数检验是利用两个配对样本对样本来自的两个总体的分布是否存在显著差异进行检验。Wilcoxon 符号秩检验[14]的原假设是两配对样本来自的两总体的分布无显著差异,计算式如下:

其中,θi表示两个对比算法在15 个数据集上的分类准确率的差,将其差值的绝对值按升序排列,对应的秩记为rank(θi),R+与R-分别表示正秩和与负秩和。将R=min(R+,R-)作为检验统计量,显著性水平α为0.05,在大样本情况下可以使用正态近似:
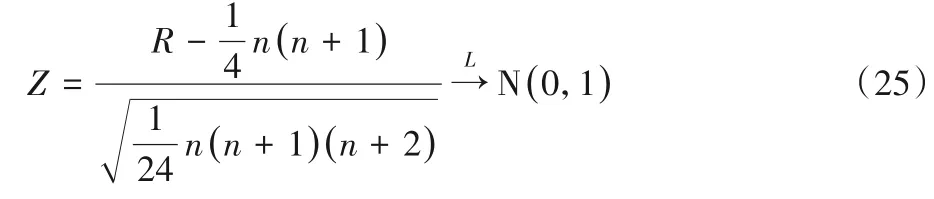
计算得到Z值以后,查正态分布表对应的概率p值,若概率p值小于显著性水平α,则拒绝原假设。
4.1.4 Friedman秩方差检验
Friedman秩方差检验[15]是一种实现多个总体分布是否存在显著差异的非参数检验方法,适用于两个因素的各种水平的组合都有一个观测值的情况。假定第一个因子有k个水平,第二个因子有b个水平,因此一共有k×b个观测值。设各总体的位置参数为θ1,θ2,…,θk,假设检验问题为:

检验统计量为:
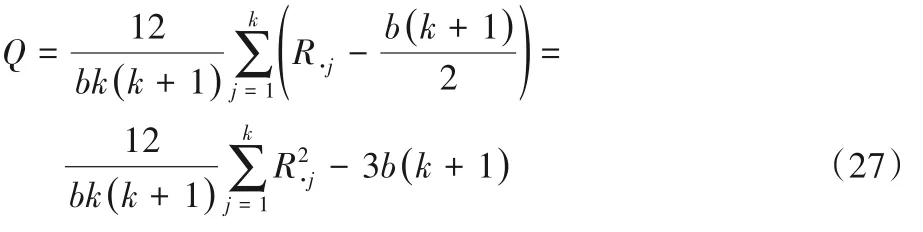
Q值近似自由度为v=k-1 的χ2分布。若实测Q<,则不拒绝H0;反之,则接受H1。
4.1.5 Hollander-Wolfe两处理比较
当Friedman 秩方差检验的分析结果有差异时,却不能表明哪两个分类器之间有差异显著性。所以本文将运用两样本(处理)间的比较[16],计算式如下:

其中,R·i和R·j分别为第i个和第j个样本的秩和。有:
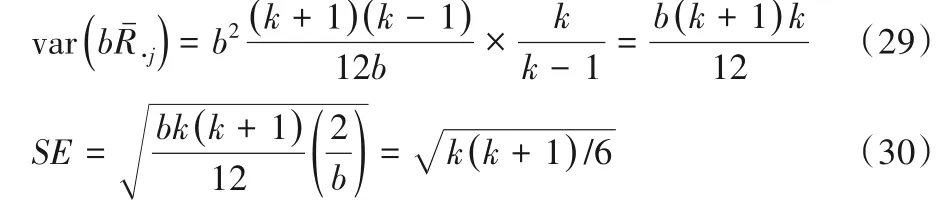
当实测|Dij|≥时,表示两样本间有差异;反之则无差异。其中,α*=α/[k(k-1)],α为显著性水平,为标准正态分布分位数。
4.2 实验结果
实验基于Intel(R)Core(TM)i7-4700 CPU@3.60 GHz 环境,算法采用Matlab 和R 语言编程实现。将本文PIW-LMPNN算法与其他8 种分类算法进行对比,表4 给出了9 种分类算法的准确率和F1 值,表5 给出了PIW-LMPNN 算法与其他对比算法的Wilcoxon 符号秩检验,表6 给出了9 种分类算法的Friedman 检验的平均等级,表7 给出了PIW-LMPNN 算法与8种对比算法的两处理的Hollander-Wolfe计算。
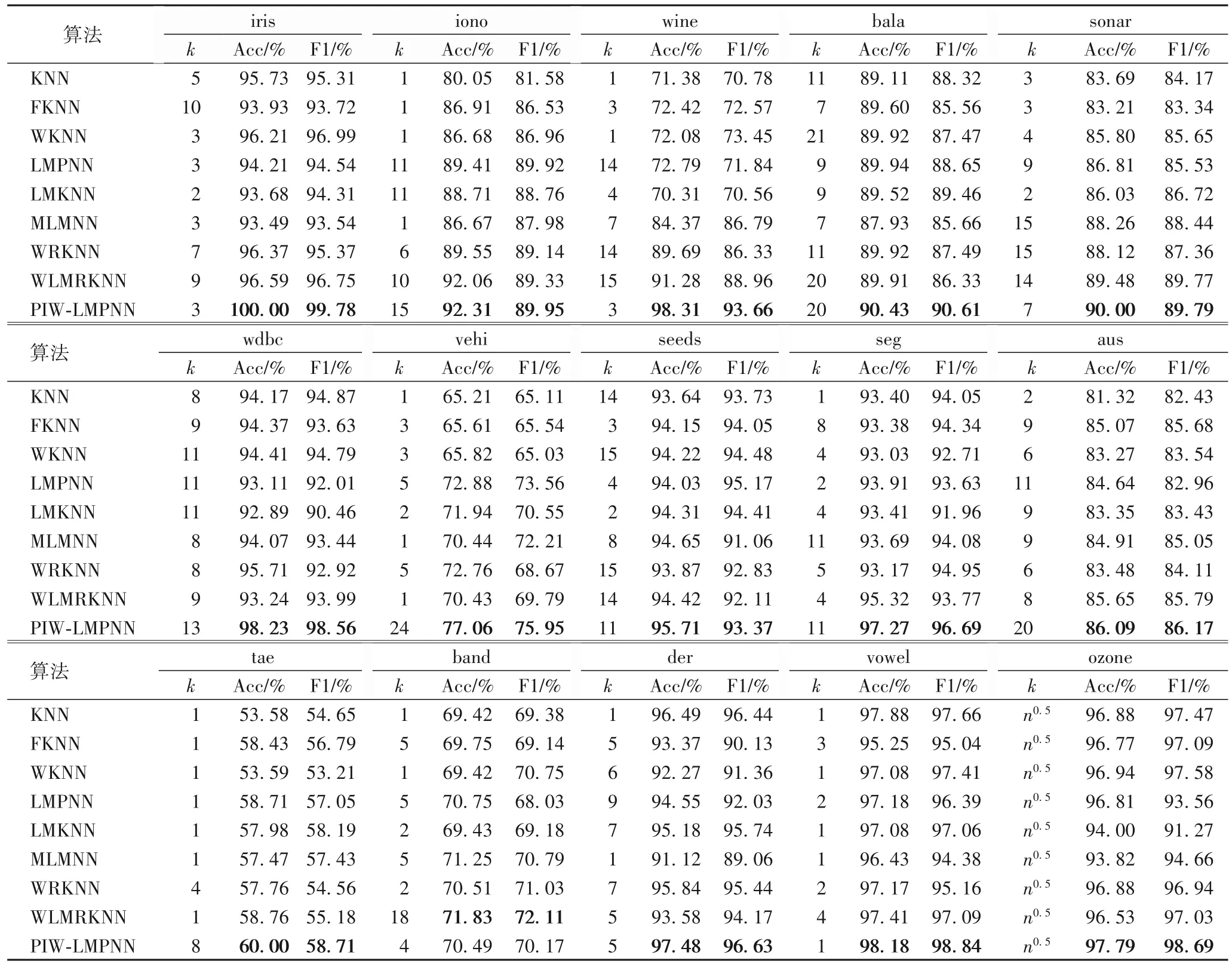
表4 在不同数据集上分类准确率、F1值及最优k值Tab.4 Classification accuracy,F1 value and optimal k value on different datasets
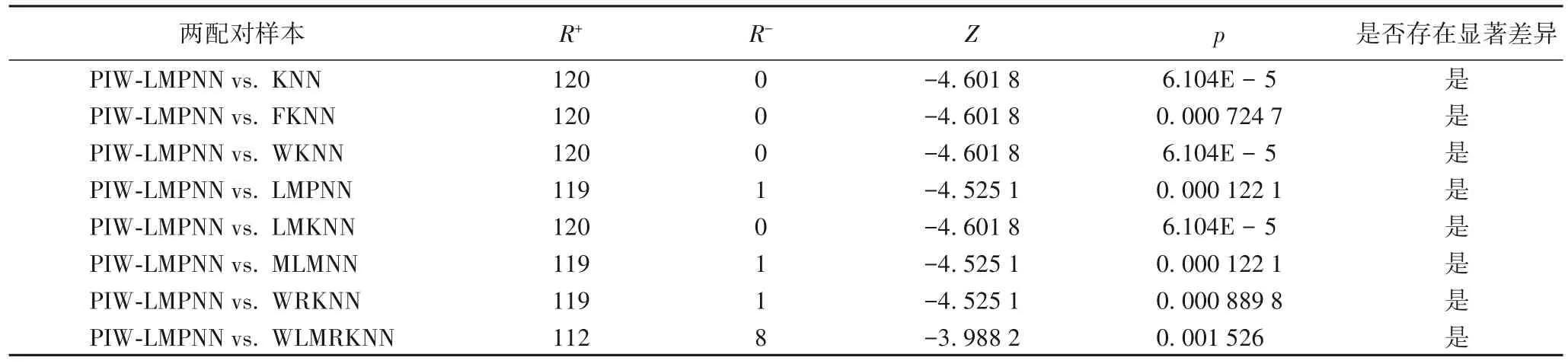
表5 PIW-LMPNN与其他对比算法的Wilcoxon符号秩检验结果Tab.5 Wilcoxon signed-rank test results of PIW-LMPNN and other comparison algorithms

表6 不同分类算法的Friedman检验中的平均秩Tab.6 Average rank of different classification algorithms in Friedman test
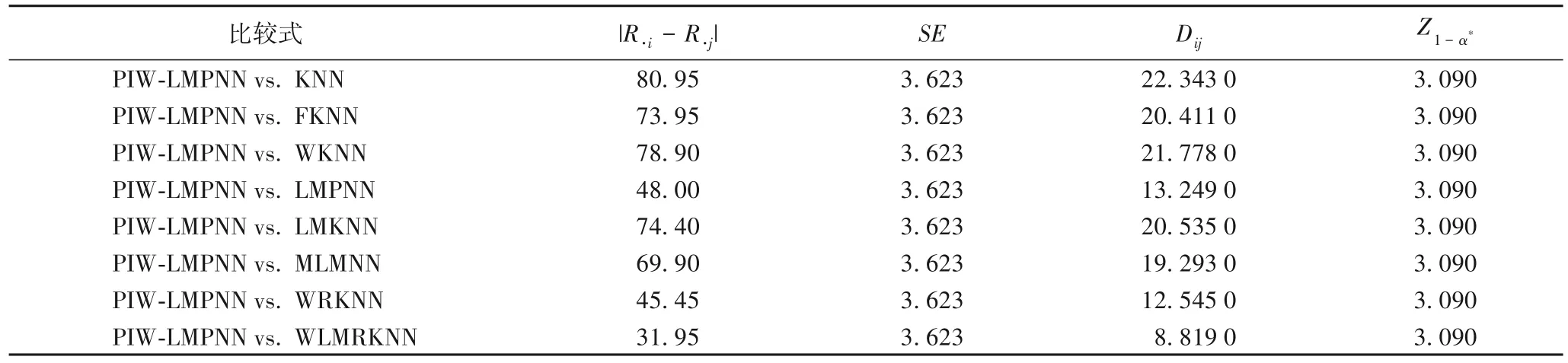
表7 在α=0.05时两处理的Hollander-Wolfe计算结果Tab.7 Hollander-Wolfe calculation results for pairwise processing when α=0.05
在本文的仿真实验中,KNN、FKNN(Fuzzy K Nearest Neighbor)、WKNN(distance-Weighted K-Nearest-Neighbor)、LMPNN[4]、LMKNN[2]、MLMNN(Multi-Local Means based Nearest Neighbor method)[17]、WRKNN(Weighted Representation-based K-Nearest Neighbor classification)和WLMRKNN 这8 种分类算法对k值均采用逐一验证的方法。具体设置如下:首先k的取值范围为1~(n表示样本数量);其次,重复5次m折交叉验证得到每个k值所对应的平均准确率,将平均准确率最高时所对应的k值选择为最优k值。根据文献[11]可知,当H的值取为100 时,目标函数的最大评估次数(maximum number of Fitness Evaluations,FEs)为1000×d,在大多数数据集上取得了较好的效果。
4.3 结果分析
在表4 中给出了PIW-LMPNN 算法和其他8 种分类算法在15 个数据集上的最优k值、分类准确率以及F1 值。由表4可见,PIW-LMPNN 在除band 数据集以外的14 个数据集上的分类准确率均高于其他比较算法。band数据集在本文算法中的分类准确率为70.49%,虽然低于WRKNN 和WLMRKNN 算法,但仍高于其余6 种算法的准确率。除此之外,还可以看到PIW-LMPNN 算法在iris、wine、wdbc、vehi、seg 和der 这6 个数据集中的分类准确率得到了明显的提升。PIW-LMPNN 在15个数据集中获得了最高的平均准确率(如图3 所示)。除此之外,由表4 可知,对于实验所选取的15 个数据集,在9 个算法中,14 个数据集的最好的F1 值都是由本文所提出的PIWLMPNN 算法得到的,也就是说,本文算法的精确率和召回率的综合性能较好。整体而言,PIW-LMPNN 算法的整体性能优于其他对比算法,所提算法的分类准确率和F1值分别最大提高了约28个百分点和23.1个百分点。
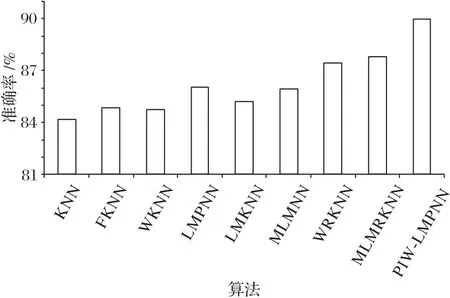
图3 不同分类算法的准确率比较Fig.3 Accuracy comparison of different classification algorithms
表5 给出了本文算法与所有对比算法的Wilcoxon 符号秩检验的结果。由表5 可知,R+的值远远大于R-的值,检验统计量Z的值小于-1.96,概率p值均小于0.05。Wilcoxon 符号秩检验结果表明,在显著性水平α=0.05 的条件下,PIWLMPNN算法的分类性能明显优于其他对比算法。
在Friedman 秩方差分析法中,首先将表4 中的所有算法在每一个数据集上的分类准确率进行排序,排名越大,其分类结果越好。在表6 中列举了每个分类算法的平均排序,PIWLMPNN 算法的平均排序Ri和其他对比算法的平均排序有较大的区别。实际测量Q=52.554 >=15.507,故接 受H1,认为9个分类算法存在显著差异。
Friedman 秩方差分析法已检验出分类算法之间有差异,接下来将进一步研究本文算法与每一个对比算法两两之间是否存在差异。由表7中9种分类算法性能比较结果可知,本文算法与其他8 种对比算法有显著的差异。Friedman 秩方差分析和Hollander-Wolfe两处理比较表明了本文算法和基于KNN的分类算法是不同的,并且PIW-LMPNN 算法的分类性能明显优于其他对比算法。
5 结语
LMPNN 是一种有效的分类算法。在每一类中,能够根据选取的k个近邻计算得到测试样本的伪近邻,进而通过决策函数预测测试样本的类别。但是,该分类算法依赖于预先设置的k值,而且忽略了每个属性对分类结果的不同的重要影响程度,将每个属性同等对待。针对这些问题,本文提出了一种参数独立的加权局部均值伪近邻分类(PIW-LMPNN)算法。该算法将SHADE 算法和LMPNN 算法结合,首先对训练集样本进行优化得到最佳k值和一组与类别相关的最佳权重,然后计算样本间的距离时赋予每类的每个属性不同的权重进行分类。
在15 个实际数据集上的实验结果表明,改进后的分类算法克服了LMPNN 算法对k值的敏感性和均等对待特征属性的不足,且具有较强的泛化能力。下一步的主要工作是研究所提算法在复杂实际问题中的应用。

