基于联合动态剪枝的深度神经网络压缩算法

张明明，卢庆宁，李文中，宋 浒

（1.国网江苏省电力有限公司信息通信分公司，南京 210024；2.计算机软件新技术国家重点实验室（南京大学），南京 210023）

（∗通信作者电子邮箱qnlu@smail.nju.edu.cn）

0 引言

近年来深度学习发展迅猛，其在图像识别、语音识别、文本翻译等多领域的应用，在国内外学术和工业界都获得了广泛的关注。然而深度神经网络（Deep Neural Network，DNN）通常需要大量计算开销，其模型的复杂度、高额的存储空间以及计算资源消耗导致其难以被应用在计算资源、能源受限的移动设备中。例如经典的图像分类网络VGG16［1］，参数数量多达1.3 亿，占用存储空间500 MB，需要进行309 亿次浮点运算才能完成一次图像识别任务。文献［2］指出，深度学习神经网络中存在很大程度的冗余，仅使用很少一部分权值就可以预测剩余的权值。因而，模型压缩（Model Compression，MC）［3］在理论上存在可行性，在现实中也存在着必要性。

模型压缩的最终目的是降低模型的复杂度，减少模型的存储空间，并加速模型的训练和推理。因而，其涉及到多方面的不同问题，包括优化算法、计算机架构、数据压缩、硬件设计等。模型压缩的主要方法有低秩近似、网络量化、知识蒸馏、紧凑网络设计，以及网络剪枝［4-5］。

作为模型压缩的一个分支，神经网络剪枝技术通过移除不重要的分支，降低大型神经网络计算消耗，使得其可以在移动设备上运行。如图1 所示，网络剪枝采用某种衡量标准，移除网络中一部分权值，或者移除一部分权值间的连接。因而，如何衡量权重的重要性成为了算法的核心问题。

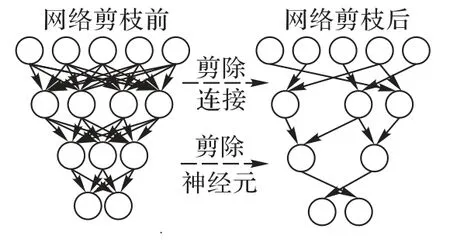
图1 网络剪枝示意Fig.1 Schematic diagram of network pruning

较早的剪枝工作侧重于权值，通过移除不重要的神经元，并对网络进行再训练，微调至收敛。Han 等［6］设计了深度压缩、结合剪枝、量化和哈夫曼编码三种方法，在AlexNet上获得了35 倍的压缩比。国内针对权值剪枝也有广泛的研究，巩凯强等［7］提出了基于统计量的网络剪枝结合张量分解的神经网络压缩方法，选择均值和方差作为评判权值贡献度的依据，有利于模型在资源受限的嵌入式设备中的部署。王忠锋等［8］则以梯度作为评判权值重要性的依据，移除模型中小于阈值的梯度对应权值，并且通过再训练恢复模型容量的损失。

然而，针对权值的剪枝会导致网络中出现大量不规则的零，卷积核成为稀疏张量，模型趋向于非结构化。针对非结构化剪枝的局限性，Li 等［9］设计了通道剪枝算法。作为一种结构化的剪枝算法，通道剪枝设计某种标准衡量卷积核的重要性，并完整地剪除不重要的卷积核及其对应的特征图，从而不会出现大部分权值被剪除而留下稀疏张量的情况。Liu 等［10］设计了网络瘦身，着眼于批标准化层中的缩放因子，在训练过程中对其施加正则约束，使得模型在训练中朝向通道结构稀疏的情况不断调整。

以上算法可以统称为静态剪枝算法，其相同点在于:被剪枝的参数从模型中永久移除，后续不再参与推理和训练。尽管网络中大部分参数是多余的，静态剪枝算法仍然会永久性地移除一部分关键性参数，无论采取何种评判标准都难以避免误剪枝，这样必然导致网络容量的损失。相较于静态剪枝算法，动态剪枝的目的是保留被剪枝部分的能力，避免永久性的剪枝导致的模型容量降低。He 等［11］提出的软通道剪枝是较为典型的动态剪枝算法，允许被剪除的卷积核参与之后的迭代更新。Guo 等［12］提出的动态外科手术，采用了剪枝与嫁接相结合算法，将剪枝工作融合到训练的过程中，利用嫁接修复误剪枝的神经元连接。

另一类算法统称为动态剪枝，其特点为不永久性地移除任何参数，转而根据输入图像的特征，动态地选择网络的一部分参与运算，以降低模型的复杂度。类比于神经网络的一种常用的正则化算法Dropout［13］，其基本思想是随机丢弃部分神经元，降低特征提取的共同作用影响，用于避免过拟合，提高泛化能力。动态剪枝不同在设计某种标准用来衡量输入图像与卷积核的关系，而非简单地随机丢弃。Gao 等［14］指出，对于特定的输入图像，能够被激活的卷积核是存在并有限的。由Hua等［15］提出的通道门控网络结构，通过构建通道门控模块，设定可自主学习的门控函数，提取输入图像特征并选择对应的通道参与卷积运算。Gao 等［14］提出了特征加速压缩，利用预测网络控制分类网络的结构，并和分类网络一同训练、学习。然而，动态剪枝算法的独特之处——动态选择，也恰恰制约了其压缩网络的能力。由于动态剪枝算法根据输入图像的特征选择被激活的卷积核，考虑到输入图像是未知的，被激活的卷积核也是未知的，卷积核很难被永久性地移除，这也导致了网络压缩比明显小于静态剪枝算法。

基于传统的静态剪枝和动态剪枝存在的一系列问题，本文提出了一种联合动态剪枝算法，可以综合分析卷积核与输入图像的特征。本文的主要工作如下:

1）提出卷积核动态剪枝算法，基于卷积核的特征，永久性地剪除深度神经网络中的一部分参数，同时尽可能地保持模型容量。

2）提出通道动态剪枝算法，基于输入图像的特征，在不移除深度神经网络参数的前提下，选择网络的一部分参数参与运算，以降低复杂度。

3）将卷积核动态剪枝与通道动态压缩有机结合，综合卷积核和输入图像的特征，保持模型容量和复杂度的平衡。

1 联合动态剪枝算法

1.1 网络结构定义

本文工作主要基于深度学习神经网络中的卷积神经网络（Convolutional Neural Network，CNN）进行。CNN 被广泛运用于图像分类、目标检测、异常检测等方面，对于图像数据具有很高的泛用性。CNN可以被参数化表示为:

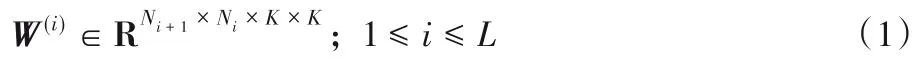
其中:W（i）代表第i个卷积层的权值张量；Ni代表第i层的输入通道数量，Ni+1代表第i层的输出通道数量，也就相当于第i层的卷积核数量、第i+1 层的输入通道数量；K×K代表卷积核大小；L代表网络卷积层的总数。第i个卷积层的卷积运算的过程，也就是Ni+1个三维的卷积核作用于输入特征图，每一个卷积核生成一个对应的特征图，将其转化为输出特征图，并作为第i+1个卷积层的输入。

因而在剪枝算法中，若卷积核Fi，j被移除，对应的特征图也会被移除；若卷积核Fi，j被置零，对应的特征图也会被置零。假设第i个卷积层的卷积核剪枝率为Pi，由于该层卷积核总数为Ni+1，则有Ni+1Pi个卷积核被移除。该层的卷积核个数从Ni+1减少为Ni+1(1-Pi)，进而输出特征图的大小也缩减为Ni+1(1-Pi)×Hi+1×Wi+1，第i+1 层的输入通道数也会缩减为Ni+1(1-Pi)。也就是说，第i层和第i+1 层的计算开销都会减小为原先的1-Pi倍。

值得注意的是，若卷积核被永久性剪除，那么特征图的大小也会永久性地改变；但如果只是将卷积核置零，那么对应的特征图也被置零，然而输出特征图的大小并没有变化。以图2 为例来说明。如果永久性移除浅色的卷积核，那么对应的浅色特征图也被移除，输出通道数量减少，进而使得下一卷积层每一个卷积核的通道数也减少。如果将深色的卷积核置零，那么对应的深色特征图也被置零；然而，由于深色卷积核并未被剪除，网络的结构没有发生变化，因而下一卷积层的卷积核不受到影响。也就是说，将卷积核置零可以在不改变网络结构的情况下影响到网络的输出，这也就是卷积核动态剪枝算法的核心思想。

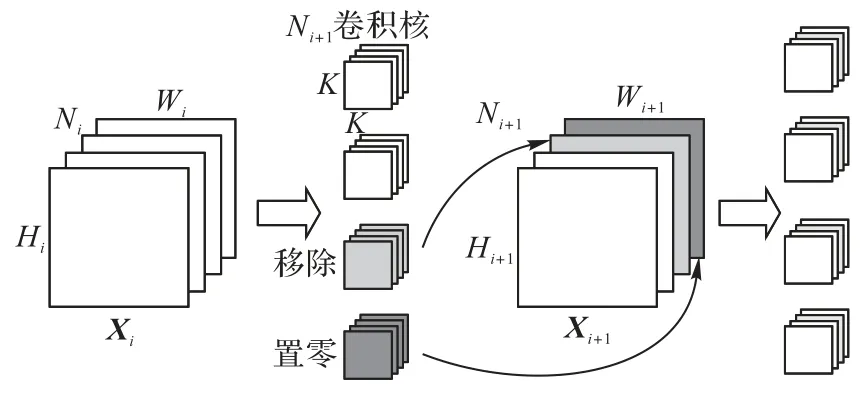
图2 移除和置零卷积核对输出特征图的影响Fig.2 Influence of removing and zeroizing convolution kernels on output feature map

以上介绍了卷积神经网络中典型的卷积层定义，然而实际训练和推理中，一般在卷积层之后紧跟批标准化（Batch Normalization，BN）［16］和激活操作，以抑制梯度消失、使神经网络更好地拟合非线性数据，并加快训练速度。一个包含BN和线性整流函数（Rectified Linear Unit，ReLU）［17］激活操作的卷积层完整定义如下:

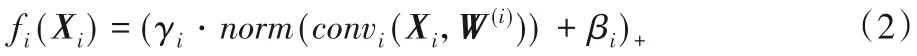
其中:Xi代表第i个卷积层的输入特征图；norm代表标准化操作；γi和βi分别代表可训练的参数缩放因子scale和偏置offset。convi（Xi，W（i））代表第i层的卷积操作，利用权值张量W（i）作用于输入特征图Xi上。这里的“·”和“+”运算均基于张量元素，(z)+=max{z，0}代表ReLU 函数激活操作。联合动态剪枝算法主要考虑卷积运算的优化，也就是convi（Xi，W（i））的相关操作，这也是卷积神经网络中运算量最大、复杂度最高的部分。

1.2 算法框架

考虑到传统的静态剪枝算法会造成模型容量不可逆的降低，而现有的动态剪枝算法尽管保持了模型容量，却没有较大幅度地降低模型的复杂度。模型的容量和复杂度，是目前研究中普遍遇到的一个两难问题。针对这个问题，本文提出了联合动态剪枝算法。联合动态剪枝算法分为卷积核动态剪枝和通道动态压缩两个部分，但二者并非互相割裂，而是相辅相成，共同完成网络剪枝的工作。

首先，针对卷积核自身的特征，设计卷积核动态剪枝的算法，用于永久性剪除部分卷积核，以提升压缩比。剪枝标准为L1 范数，但不直接把这些卷积核从网络中删除，而是将对应通道置零后继续训练学习，允许置零的卷积核在反向传播中更新，直到收敛为止。针对输入图像特征，设计通道动态压缩的算法，将输入图像采样后经过线性变化预测通道的重要性，然后将对应通道的结果置零，也就相当于在没有改变网络结构的情况下，跳过了一部分的卷积运算。

以图3 为例来说明联合动态剪枝算法的流程。定义卷积核动态剪枝率为β，通道动态压缩比为α。为了平衡准确率和模型复杂度，规定2β=α+1，也就是将完整的网络压缩比分为两个步长，利用卷积核动态剪枝的算法压缩网络至β，利用通道动态压缩的算法压缩网络至α，综合获得需要置零的所有通道。值得注意的是，这两步是同时在训练的过程中进行的，实际上并没有先后顺序之分。图3 中浅色的卷积核被置零，并允许在后续训练中更新；深色部分并非原先网络的参数，而是输入特征图经过预测网络处理后获得的通道重要性预测结果，这个结果被乘到卷积运算的结果中。

图3 联合动态剪枝算法框架Fig.3 Framework of combined dynamic pruning algorithm

卷积核动态剪枝和通道动态压缩并非相互独立，而是有机融合；并非一前一后，而是同步进行。首先，卷积核动态剪枝可以基于模型参数选择一部分重要性较小的卷积核置零。但是，并不直接将置零的卷积核传递到通道动态压缩中去，否则就等同于先卷积核动态剪枝，后通道动态压缩，这样会导致两种方法存在先后次序，后者难以影响到前者。联合动态剪枝算法选择让两步剪枝操作同步进行，并且在反向传播的时候同步更新，实际上每一个剪枝操作误剪枝的信息都会被反馈到另一个操作中去。

不难作出如下的推断:卷积核动态剪枝置零的卷积核（通道），在通道动态压缩之中也被动态剪除，如图3 中所展示的，浅色通道是深色通道的子集。通道动态压缩基于输入图像作预测处理，不考虑卷积核动态剪枝的结果，因而直观感受上可能出现卷积核动态剪枝置零的卷积核不包含在通道动态剪枝之中的情况。但是，在不断训练收敛的过程中，卷积核动态剪枝的结果会趋近于一部分特定的卷积核，而通道动态压缩选择参与运算的卷积核，必定不可能收敛到这些被置零的卷积核，否则通道动态压缩的结果一定是次优的。这样，模型最终训练完毕后，卷积核动态剪枝的结果收敛成为通道动态压缩的一个子集，可以最大限度地平衡模型的准确率和复杂度。

1.3 卷积核动态剪枝

卷积核动态剪枝算法的设计目的，是从模型中永久性地移除一些重要性较低的卷积核，同时最大化地保持模型的容量。对于同一卷积层的每一个卷积核，设计特定的标准sj衡量其重要性。本文选择了L1范数，也即卷积核张量中权值的绝对值之和∑|Fi，j|。从直观的层面来看，权值较小的卷积核，对应的输出特征图数值也较小，也即影响力不如同一层其他的特征图。实验结果也表明，剪除绝对值较小的卷积核效果优于随机剪除和剪除绝对值较大的卷积核。卷积核重要性的标准也有不同的选择，如L2 范数，也即卷积核张量中权值的平方之和再开平方。然而此方法的动态判断核心在于迭代更新的过程，而非单次迭代中复杂的衡量标准，并且复杂的衡量标准并没有带来表现上的提升，因而最终仍然选择了L1范数作为评判标准。

考虑到永久性的剪枝会导致模型容量不可逆的降低，仅在最后一步永久性剪除卷积核，并且尽可能剪除少的卷积核，以保持模型容量。将卷积核的剪枝工作融入网络训练的过程中，对于每次迭代中重要性较小的卷积核，并不永久性地剪除它们，而是将其置零，并保持网络结构的不变。被剪除的卷积核对网络训练产生影响的同时，允许这些卷积核在反向传播中被更新。这样，如果存在被误剪枝的卷积核，这些卷积核将会在反向传播中被更新为较大的权值，从而在后续的评判中获得较高的重要性，不再被误剪枝。在不断迭代训练的过程中，偶然误剪枝的卷积核被恢复，使得每次被剪除的趋向于收敛到Ni+1(1-β)个固定的卷积核。最终，永久性剪除这些不重要的卷积核，这样便完成了卷积核动态剪枝的工作。在先前的分析中提到，卷积核动态剪枝直接影响到网络中的部分卷积核，但是并不将结果直接地传递给通道动态压缩，而是让后者在训练中不断自主学习，同时其本身也不断更新置零的卷积核，两种方法共同完成剪枝的工作。具体算法如算法1所示。

算法1 卷积核动态剪枝。

输入 训练数据X，卷积核动态剪枝率β，模型，1 ≤i≤L；

输出 卷积核动态剪枝后的模型W*。

1.4 通道动态压缩

通道动态压缩，即在不永久性移除模型中的任何参数的情况下，通过动态选择模型的一部分参与运算，从而加速训练和推理的过程。因而最关键的是利用某种方式，针对特定的输入图像，动态选择特定的神经元参与运算。考虑到结构化剪枝相较于非结构化剪枝的优势，仍然以通道为单位进行剪枝。具体方法是构建一个较小的线性变化神经网络，称之为预测网络，用于建立输入特征图与卷积核的关系，预测并选择部分的通道参与卷积运算，以保持模型的容量。

首先需要提取输入图像的特征。如果将分类网络的输入图像完整地作为预测网络的输入，那么整个模型的复杂度将会极大提升，甚至抵消了剪枝所带来的收益。因而，必须尽可能地将输入图像压缩到可接受的大小，同时保留其特征，用于预测网络的输入。这里选择了下采样方法，也就是缩小图像的尺寸。经过实验，可以发现全局平均池化（Global Average Pooling，GAP）［18］的效果最好。GAP 是一种简单而实用的正则化方法，也就是取二维图像所有元素的平均值，近年来也有研究认为其拥有较好的提取图像特征的能力。将其应用到三维的特征图中，有下采样函数:

然后，需要建立下采样后的输入图像与卷积核之间的关系。和卷积核动态剪枝相反，这一步不需要显式地考虑卷积核本身的参数，而是构建一个线性变化神经网络，称之为预测网络，利用其去预测输入图像与卷积核的关系。预测网络的值被附加到分类网络的输出中，并随着反向传播自动更新。线性变化的函数如下:

线性变化预测网络，也就是一个额外的全连接层，拥有权重φi和偏置ρi两个可学习的参数。预测网络的输入为ss（Xi），也就是Ni个元素的向量，每个元素代表着当前卷积层输入图像的一个通道的特征。经过线性变化，其输出为Ni+1个元素的向量，每个元素代表着当前卷积层每个卷积核针对该输入图像的重要性。较大的元素代表对应通道被输入图像激活的程度越高，也就越为重要。

获得了每个卷积核的重要性，之后需要基于通道动态压缩比α，在原先完整的输出特征图中，消除一部分通道的输出。基于一个简单的k-胜者通吃（k-winners-take-all）操作，也即选择向量中k个最大元素，将其余元素置零。这样，重要性较低的Ni+1(1-α)个通道将不参与卷积运算，也就完成了剪枝的操作。

由于预测网络需要和分类网络一同更新，因而预测网络的结果也需要被附加到分类网络的输出中去。基于之前包含BN 和ReLU 操作的卷积层完整定义，将BN 层的γ参数替换成为预测网络的输出，也就是gi（Xi）:

至此，便完成了动态通道压缩的工作。回顾完整的算法流程，最重要的是预测网络的构建。如果设计某种算法用来衡量输入图像与卷积核之间的激活关系，利用统计特征去构建二者之间的函数变换，那么无疑是非常困难的。然而，将预测网络的结果融合到分类网络中去，利用神经网络的反向传播自发学习其中的误差，并不断优化预测的结果，既提高了预测的准确率，又避免了复杂且有可能过度的人工干涉，可以说是一举两得。具体算法如算法2所示。

算法2 通道动态压缩。

输入 训练数据X，通道动态压缩比α，模型，1 ≤i≤L；

输出 通道动态压缩后的模型W*。

2 实验与结果分析

本文所使用的实验设备基于Windows 10 系统，采用处理器Intel Core i7-9750H，显卡NVIDIA GeForce GTX 1660Ti，在虚拟环境PyCharm 2019.2.4（Community Edition），torch version 1.0.0，CUDA version 10.0下进行实验。

实验的数据集为经典的图像识别数据集CIFAR-10 与CIFAR-100。CIFAR-10 数据集由Krizhevsky 等［19］收集完成，包含60 000张彩色图像。所有图像都是32×32大小，分为10种类别，其中5/6的图像被作为训练集使用。CIFAR-100 数据集同样包含60 000 张图像，所不同的是其被分为100 种类别，每种类别的图像有600 张。100 种类别实际上被划分为20 个超类别，每个超类别包含5 种子类别。本实验仅关注子类别的正确率。

CIFAR 数据集包含现实生活中的真实物体，图像格式为3通道RGB 图像，物体的大小比例、特征、背景各不相同，具有一定的复杂性，相较于MNIST 这种简单的单通道、仅包含手写数字的数据集，更有现实意义。与更加复杂的数据集如ILSVRC2012 相比，CIFAR 数据集规模较小，不受限于机器性能，方便训练。

2.1 训练方法

选用了软通道剪枝（Soft Filter Pruning，SFP）和特征加速压缩（Feature Boosting&Suppression，FBS）两个已有的先进网络剪枝算法，与本文提出的联合动态剪枝（Combined Dynamic Pruning，CDP）算法相比，在准确率、参数压缩比等各方面作出客观的比较，以验证联合动态剪枝算法的优劣。

CDP算法训练过程如下:首先，训练一个不含联合动态剪枝操作的基本网络结构，然后将其所有的卷积层替换为联合动态剪枝的卷积层。随后，令卷积核动态剪枝率β和通道动态压缩比α均为1，微调网络至收敛。然后，不断降低α和β，令β下降步长为0.1，并保持2β=1+α的关系，最终达到需要的压缩比。例如需要压缩比为0.6 的联合动态剪枝模型，那么α=0.6，β=0.8。训练中使用256 的批大小，0.01 的学习率，每过100 个训练期学习率降低为原先的0.1，直到学习率降低至10-5停止，这些参数适用于所有的剪枝算法。对于使用者而言，只需要额外设置两个超参数α和β即可。

数据的处理上，训练集和测试集均进行了标准化处理。训练集同时也进行了随机打乱的操作，以及翻转概率p=0.5的随机水平翻转，以避免过拟合，提高模型的泛化能力。

2.2 评估标准

最直观的评判标准，即在某个特定剪枝率下，比较不同算法带来的准确率变化。定义模型的压缩比为α，剪枝率为γ，有α=1-γ。对于SFP 算法，也就是移除每个卷积层中占比为γ的卷积核。对于FBS 算法，则是对于每个输入特征图，仅有α的通道被选择参与卷积运算。对于本文提出的CDP 算法，则是利用卷积核动态剪枝置零1-β的卷积核，同时利用通道动态压缩使得α的通道被选择参与卷积运算。这样便可以在模型压缩比相同的情况下，比较三种算法的准确率。

然而，三种算法的实现不同，相同的剪枝率带来的复杂度降低也不尽相同。因而，为了更客观地衡量模型的复杂度，本文进一步选用了浮点运算次数（Floating-Point Operations Per second，FLOPs）和参数规模的压缩比两个标准。假设卷积运算利用滑动窗口实现，并且忽略非线性计算开销［20］。

对于卷积层（convolutional layer，conv），有:

其中:H、W分别代表输入特征图的宽和高；Cin、Cout代表输入和输出通道数；FLOPs代表浮点运算次数；PARA代表参数个数。假设卷积核是对称的，因而其宽与高相等，均为K。

相对地，有全连接层（fully connected layer，fc）的浮点运算次数和参数规模计算如下:

其中，I、O分别代表输入和输出通道数。

原始网络的浮点运算次数除以剪枝后网络的浮点运算次数，得到的就是FLOPs压缩比。同理也可以得到参数压缩比。为避免歧义，本节出现的压缩比如未特别说明，均代表网络压缩比，也就是对应于剪枝率的压缩比，而非FLOPs压缩比或参数压缩比。

2.3 结果分析

2.3.1 M-CifarNet实验结果

M-CifarNet［21］是一个针对CIFAR 数据集设计的8 层卷积神经网络，仅用1.3×106个参数就在CIFAR-10数据集上达到了91.37%和99.67%的Top-1 与Top-5 正确率。M-CifarNet 中所有的卷积层均采用3×3 的卷积核，pool 是一个全局平均池化层。

表1展示了M-CifarNet的网络结构，以及不同剪枝算法带来FLOPs 运算的比较。在先前的分析中，FBS 作为动态剪枝的经典算法，其并不更改网络结构，因而输出通道数是没有变化的。然而其仅选择部分卷积核进行计算，体现在FLOPs 计算上，也就是输入通道数量不变，而输出通道数量减少。因而，其FLOPs 的压缩比也是最小的。SFP 因为永久性移除了部分卷积核，因而压缩比最大。CDP 虽然也永久性移除了部分卷积核，但其移除的比例没有SFP那么大，因而取得了介于两者之中的FLOPs压缩比。

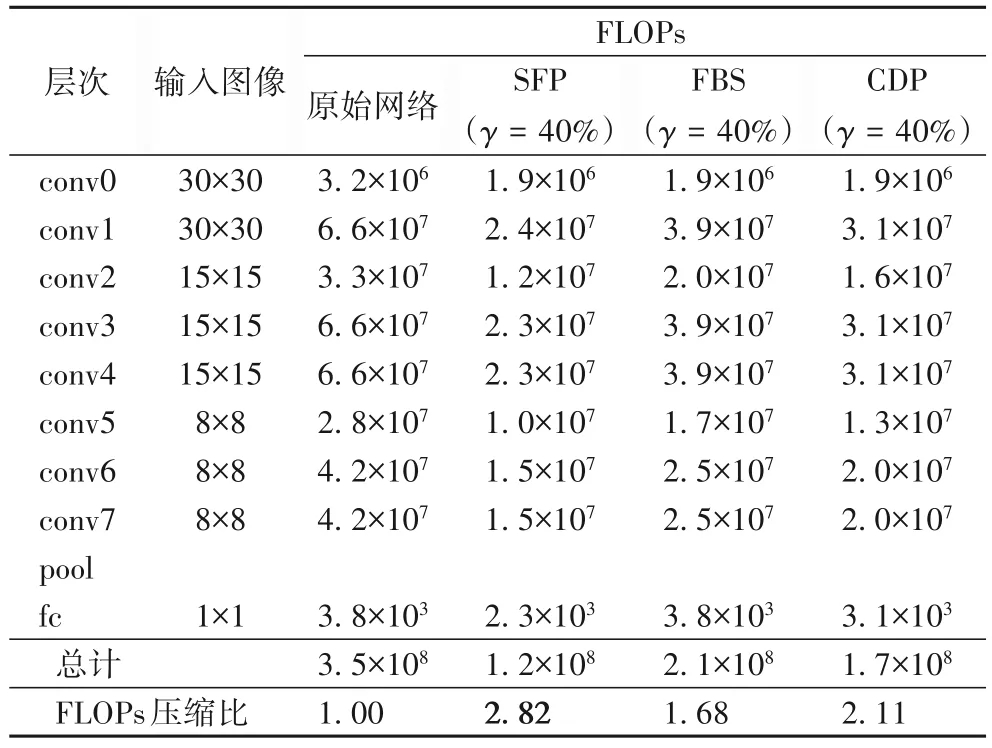
表1 M-CifarNet网络结构以及不同剪枝算法带来FLOPs运算的比较Tab.1 M-CifarNet network structure and comparison of FLOPs operations brought by different pruning algorithms

从参数规模上来看，由于FBS 和CDP 引入了额外的预测网络，因而和原始网络结构相比有额外的参数。然而相较于卷积层的参数，全连接层的参数仅占很小一部分，因而可以忽略不计，将重点聚焦在剪枝算法移除原先模型的参数数量。

令网络压缩比α从1 降低到0.2，得到的结果如图4（a）所示。由于FBS和CDP均引入了额外的全连接层用于通道重要性预测，因而在压缩比为1 时，二者准确率都超过了原始模型的准确率。总体来看，CDP的准确率明显高于前两种算法，在压缩比α≤0.6时更为明显，准确率高出了约1%以上。

2.3.2 VGG16实验结果

VGG是牛津大学视觉几何组Simonyan等［1］提出的深层次卷积神经网络模型，在2014 年的ImageNet 图像分类与目标检测比赛中获得了突出的成绩。VGG16 包含五个堆叠而成的模块，每个模块包含数个卷积层和一个最大池化层，最后是三个全连接层。其中，具有权值的卷积层和全连接层总数为16，由此而得名。表2展示了VGG16的网络结构，以及不同剪枝算法带来FLOPs 运算的变化比较。SFP 算法永久性地移除了最多的参数，因而获得了最高的FLOPs 压缩比。本文提出的CDP算法则取得了一个介于其中的FLOPs压缩比。

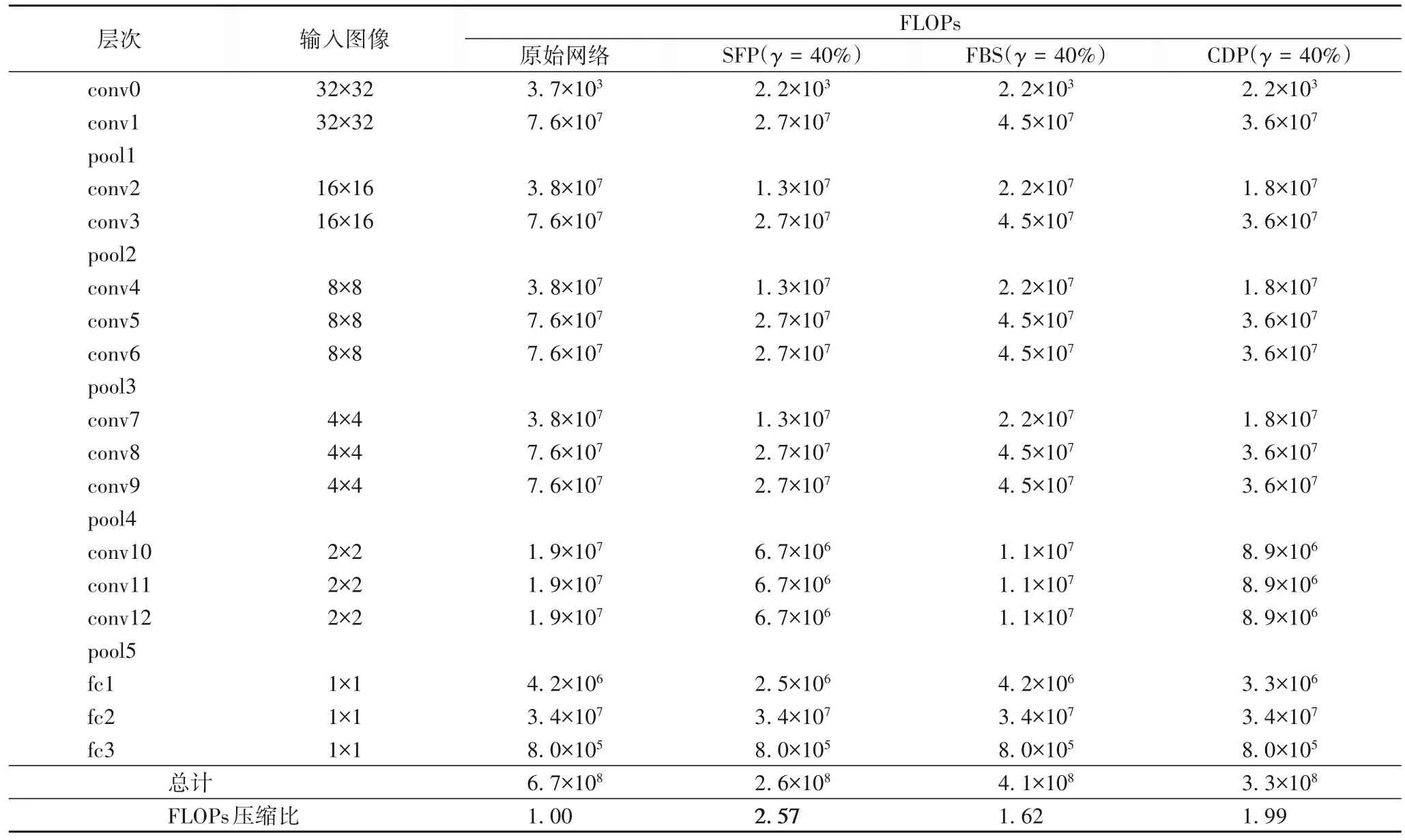
表2 VGG16网络结构以及不同剪枝算法带来FLOPs运算的比较Tab.2 VGG16 network structure and comparison of FLOPs operations brought by different pruning algorithms

和M-CifarNet 的实验类似，令网络压缩比α从1 逐渐降低到0.2，观察不同剪枝算法对模型准确率的影响，如图4（b）所示。结果表明，CDP 的准确率仍然高于前两种算法，并且在α≤0.6 时更为明显，准确率提升有0.3%～1.0%甚至更高。而永久性移除最多卷积核的SFP 算法，准确率也最低。这也验证了本文之前的假设:永久性移除卷积核会导致模型容量不可逆转的降低，从而影响准确率。

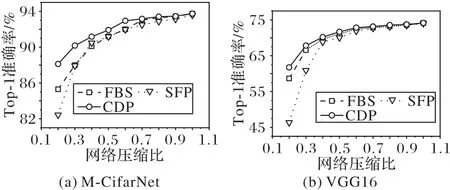
图4 不同剪枝算法带来的准确率变化Fig.4 Accuracy changes brought by different pruning algorithms

2.3.3 综合比较

以上基于相同的网络压缩比，比较了不同算法的准确率。然而，正如之前的分析，相同的网络压缩比在不同的算法中实现不同，对于网络复杂度的降低也不尽相同。偏向于静态剪枝的算法，由于永久性去除了部分参数，因而会取得更高的FLOPs 压缩比；而动态剪枝类别的算法，在FLOPs 压缩比上面相对较低。因而这里将基于相同的准确率，比较不同算法的FLOPs压缩比。

表3 展示了不同剪枝算法在M-CifarNet 上准确率、FLOPs、参数规模等指标的变化情况，表格中加粗项为准确率一致的情况下，三种算法在不同指标上取得的最好结果。注意到，这里选择的是CDP（γ=40%）、FBS（γ=30%）以及SFP（γ=20%）三种算法的特殊情况作为比较，而不是三种算法在同样的剪枝率γ下的结果。这是由于在剪枝率γ相同的情况下，FBS 和SFP 算法的准确率均低于CDP 算法，因而需要适当降低剪枝率，将准确率提升至与CDP（γ=40%）相当的情况，再针对浮点运算和参数规模的压缩比进行分析。经过实验，选择了SFP（γ=20%）与FBS（γ=30%）作为对比参考。

表3 基于数据集CIFAR-10的M-CifarNet网络结构以及不同剪枝算法的综合比较Tab.3 M-CifarNet network structure based CIFAR-10 dataset and comprehensive comparison of different pruning algorithms

可以看到，此时CDP 算法的准确率和SFP、FBS 算法基本持平，且略高于后二者。在准确率保持一致的情况下，关注FLOPs 压缩比和参数压缩比的结果。CDP 算法提供了最高的FLOPs压缩比，为2.11，SFP和FBS仅分别提供了1.57和1.42的FLOPs 压缩比。而参数压缩比上可以看到，SFP 和CDP 大致相当，均为1.57，FBS 算法由于没有永久性移除卷积核，因而对模型的参数没有造成影响。也即可以得到如下的结论:在准确率一致的情况下，CDP 算法提供了最高的FLOPs 压缩比和参数规模压缩比。

以上完成了对于压缩比和准确率的对比讨论，下面将基于CDP算法在训练中的表现作进一步的分析。选择了SFP算法和CDP 算法作对比，记录其训练过程中各项指标的变化情况，具体来说是训练集的Top-1准确率、Top-5准确率、损失，以及测试集的Top-1 准确率、Top-5 准确率、损失，并作出其随着迭代次数增加的变化曲线，如图5～6所示。

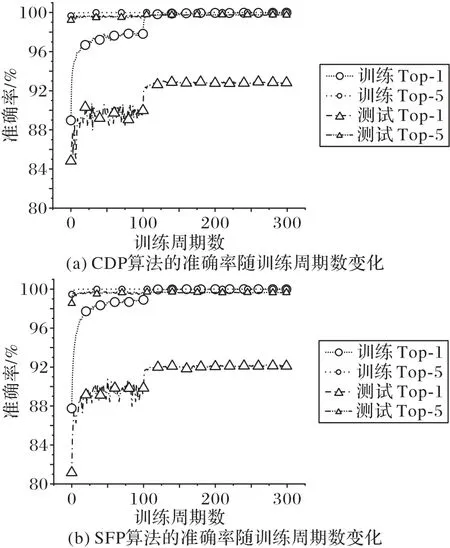
图5 不同剪枝算法带来的准确率随训练周期数的变化Fig.5 Accuracy varying with training epochs caused by different pruning algorithms

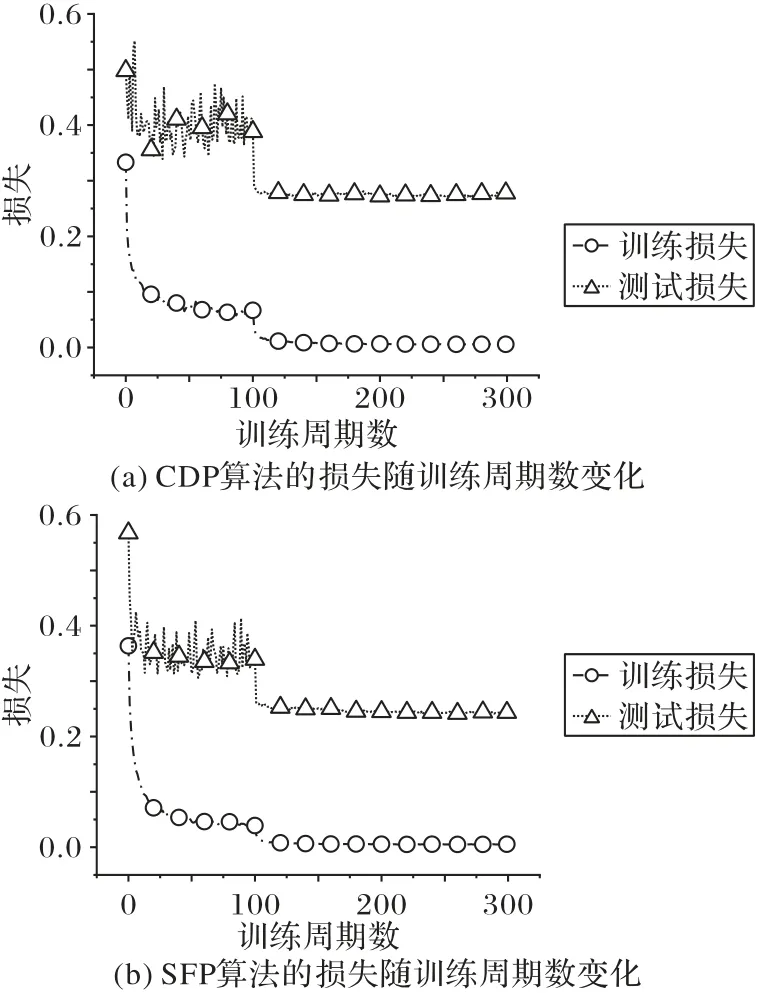
图6 不同剪枝算法带来的损失随训练周期数的变化Fig.6 Loss varying with training epochs caused by different pruning algorithms

关注到训练集的损失，CDP算法下降稍慢一些，并且震荡幅度也略微大一些，而SFP 算法的训练集损失曲线明显更为平滑。从收敛的速度来看，两种算法大致相当，在50 个训练期以后均趋近于收敛。对于本次实验而言，采用了每隔100个训练期学习率降低为原先的1/10，对于两种算法来说都已经足够。结合准确率变化可以看出，训练集的准确率变化曲线和训练的损失变化曲线形态相当。

基于以上分析，可以得出结论:在网络压缩比相同的情况下，CDP 算法拥有最高的准确率；而在准确率相同的情况下，CDP算法拥有最高的FLOPs压缩比和接近于最高的参数压缩比。相对而言，SFP 算法牺牲准确率换来了更低的模型复杂度，而FBS算法整体而言均显劣势。然而，CDP算法引入了额外的全连接层，导致其训练时震荡幅度较大，收敛速度也略慢于SFP算法。

3 结语

本文针对已有网络剪枝工作中出现模型容量损失的局限，提出了联合动态剪枝的算法，可以综合考虑卷积核和输入图像特征，动态选择网络的一部分参与运算，保持了高准确率和模型容量。相较于传统的剪枝算法，联合动态剪枝算法取得了更高的准确率和压缩比。基于M-CifarNet与VGG16的实验结果表明，联合动态剪枝分别取得了2.11和1.99的浮点运算压缩比，而与基准模型（M-CifarNet、VGG16）相比准确率仅分别下降不到0.8 个百分点和1.2 个百分点。该算法的实现分为卷积核动态剪枝和通道动态压缩两个部分，二者有机结合、相辅相成。联合动态剪枝将剪枝工作融合进训练和推理的过程中，降低了额外的开销。对于使用者而言，只需要额外设置两个剪枝率超参数，较为方便易用。

本文算法相较于现有的动态剪枝算法，无论是准确率还是浮点运算压缩比都更优；然而相较于传统的静态剪枝算法，仍然存在参数压缩比不够高、收敛较慢的情况。可以认为模型容量（体现为准确率等）和复杂度（体现为浮点运算次数、参数规模等）是一个两难问题，需要在现实场景中根据具体情况抉择。尽管对于固定的剪枝率，不需要先剪枝后微调的过程，然而为了更好的剪枝效果，联合动态剪枝算法仍然需要逐渐下调剪枝率直到达到需要的压缩比。另外，因为工作环境和机器受限，没有测试更加复杂的数据集和网络结构，也没有在实际的移动设备中测试剪枝算法，这些是值得完善和改进的地方。