弹道导弹惯性测量系统精度指标自适应分配方法
魏宗康,唐文浩,高荣荣,周 姣
(北京航天控制仪器研究所,北京100039)
0 引言
弹道导弹及运载火箭制导系统的任务是使导弹的弹头准确地命中目标,使运载火箭的有效载荷进入预定轨道。要完成这一使命,一方面要敏感并计算出火箭的实时飞行状态;另一方面要给出指令,操纵火箭改变其速度矢量,按规定要求关闭发动机或使其推力终止。要命中目标或进入预定轨道,就要求惯性制导系统高精度地完成其任务,弹道导弹及运载火箭制导系统的命中精度是反映其武器和导航系统性能及科技水平的重要评定依据。惯性测量系统作为惯性制导与导航系统的核心部件,对于弹道导弹的命中精度有着决定性的影响。
为了提高惯性导航系统的精度,需要对惯性导航系统进行误差分析,找出对导航系统精度有影响的主要误差源,并确定主要误差源对系统精度的影响占比大小。同时,在给定导航精度值的条件下,还需要对误差源进行精度指标分配,即根据总体精度指标要求并考虑到当前生产及科研力量的水平,对影响精度指标比较大的提出要求;对容易提高的误差因素,适当提高要求。若分配的精度总和不满足总的指标时,则可采取不同的提高精度的措施,使达到总精度要求。在弹道导弹惯性导航系统研究中,对惯性测量系统做误差分析和精度指标分配,一方面为惯性导航系统的研究与设计提供了理论参考依据,另一方面对弹道导弹等武器系统进行预前的误差分析,防止了因未知误差而导致的损失与误判,在实际应用中具有一定的安全和经济效益。
目前,针对惯性测量系统的误差分析,大多文献只对个别的误差项进行研究[1],并没有对惯性测量系统尤其是惯性器件存在的所有误差源进行全面的评估与分析。另外,对于精度指标调整和分配方法,文献[2]给出了一种精度指标均匀分配的方法,即将总的精度指标均等地分给每一个误差项;文献[3]给出了一种基于灵敏度的比例分配原则和动态条件下的惯性导航系统误差分配方法,此方法考虑了不同误差源对精度的影响情况以及个别不同惯性器件等级下的CEP精度值。但是,这些方法只是基于已存在的惯性测量系统的误差系数进行分析,并没有考虑到现有误差系数值不满足精度指标要求时如何对误差系数进行动态的自适应调整与误差分配。此外,目前在精度指标分配方面的精度评估准则一般均选取圆概率误差(CEP),而实际导弹的落点并非一定遵循落点位置偏差相等的情况,更多是横纵向位置偏差不等的情况,而现文献中对这种情况的研究少之又少[4]。
针对弹道导弹惯性测量系统精度指标分配方法存在误差分析不全面、误差分配方法简略、精度原则的选取单一等问题,本文提出了一种弹道导弹惯性测量系统精度指标动态自适应的分配方法。该方法解决了惯性测量系统在不同精度评估准则、不同精度要求下的误差分析与误差调整和分配过程,并给出了最终精度指标分配样例,此方法实现了惯性系统精度指标地快速、有效调整与分配。
1 弹道导弹惯性测量系统的落点精度误差分析
1.1 制导工具误差
对于惯性导航系统来说,影响其精度的因素有很多,包括初始对准误差、惯性器件误差和导航算法误差等。在所有误差源中,惯性器件误差影响最大,大约占据了总误差的90%的以上,且惯性器件误差中的各项误差种类繁多,较为复杂,因此对惯性器件误差的各来源进行分析十分必要。
影响惯性制导落点精度的主要误差是工具误差[5],包括初始对准误差、陀螺误差和加速度计误差。表1列出了影响弹道导弹落点精度的60项误差系数。
1.2 导弹落点偏差及标准差计算方法
弹道导弹命中精度以其落点的横向偏差ΔH和纵向偏差ΔL作为评价指标,弹道导弹在关机点后主要依靠惯性飞行,导弹在主动段关机点时的状态参数决定了落点的大致位置。假定地面坐标系和发射坐标系重合,文献[5]~文献[8]给出了惯性坐标系下导弹主动段关机点的状态参数矢量,即三维位置误差ΔX、ΔY、ΔZ和三维速度误差Δvx、Δvy、Δvz,将已知状态参数线性化后得到以下横向、纵向偏差的状态线性方程

设ci(i=1,2,3,…,60)为表 1 给出的惯性测量系统误差系数,将式(1)表示的误差方程对ci展开得到

式(2)、 式(3)中,δLi为由ci引起的纵向偏差分量,δHi为由ci引起的横向偏差分量,为弹道设计总体部门给出的主动段环境函数,和为总体部门给出的关机点后导弹自由飞行至落点的被动段环境函数。
总的落点偏差计算公式如下

式(4)、 式(5)中,FL和FH为横纵向总偏差对应的1×60的环境函数矩阵,C为60×1的误差系数矩阵,即

设上述60个误差系数相互独立、不相关,由以上每一项偏差值计算得到的纵向、横向落点位置的方差值如下
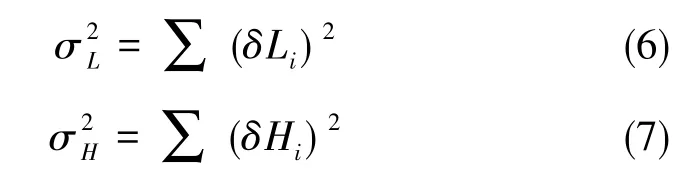
因为每一项误差源对总的落点精度具有不同的影响,有的误差源影响较大,有的误差源几乎不产生影响,可以忽略。并且,考虑到当前生产水平,没有办法对所有的误差项都进行完善与改进,只能对其中影响因素较大的项进行处理,因此计算每项误差源占总误差的比值十分有必要。每项误差源占总误差的比值计算公式如下
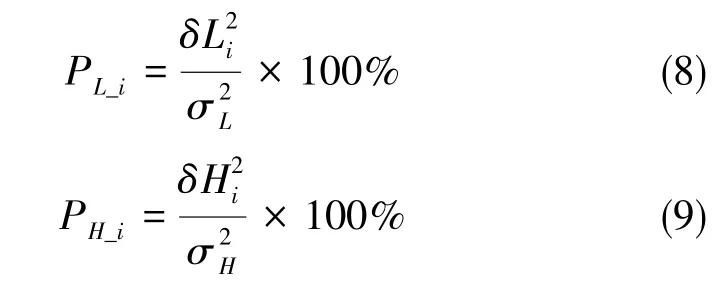
根据总体部门给出的惯性测量系统误差系数初值矩阵C和横纵向环境函数矩阵FL和FH,将其带入到式(2)、 式(3)、 式(6)~ 式(9)中计算各项误差源的占比值,如图1所示。由图1可知,不同误差源占比各不相同。因此,需要将影响误差精度较大的项选出,根据精度要求值进行调整。
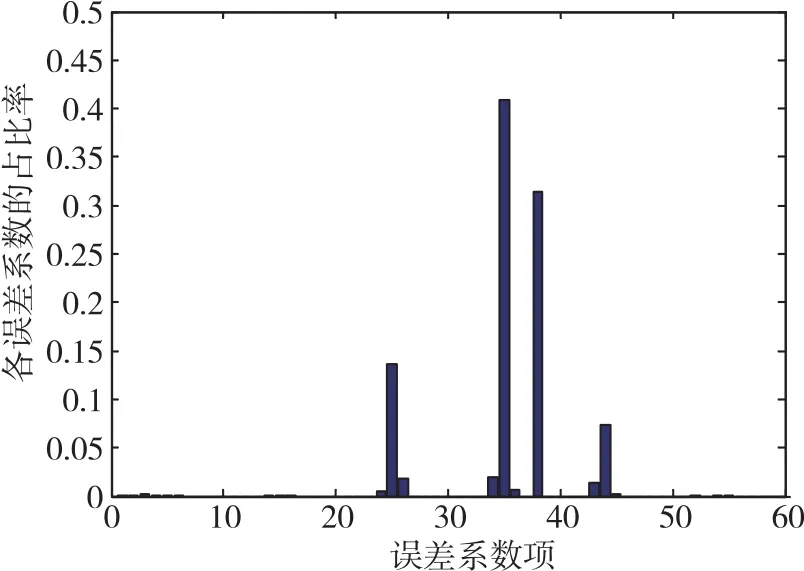
图1 各误差源占比分布Fig.1 Navigation errors ratio of each instrumental error
2 惯性测量系统精度指标调整与分配
上一节对惯性导航系统的误差源特别是惯性器件的误差进行了分析,明确了惯性测量系统各误差参数对导弹落点总精度的影响情况。然而只进行误差分析是不够的,还要对给定导航精度下的惯性测量系统误差参数进行精度指标调整与分配,确定各误差源的范围,即误差分配。误差评估为误差分配提供了基础和依据,误差分配的结果需要误差分析作检验。
首先,根据已经得到的各项误差源对导弹落点精度的影响占比情况选出对精度指标影响较大的误差系数项。在实际弹道导弹系统设计中,总体部门会针对不同情况的弹道导弹需求提出不同的精度要求。因此,通常需要对现有的误差源经验值进行调整,得到最优分配下的误差精度指标,总体部门根据最优的误差指标对惯性器件进行相应的改进与补偿。
弹道导弹落点精度的评估手段目前采用较多的为圆概率误差(CEP),即落点位置落入以散布中心为圆心的某个圆内概率为50%时的圆的半径R称为CEP。在横纵向偏差近似相等或比值相差不大时,圆概率误差(CEP)具有很好的通用性。但是当落点位置在横纵向相差较大时,CEP精度指标不能直观、准确地反映落点的分布情况,因此需要借助椭圆概率误差(Elliptic Error Probable,EEP)来作为落点的精度指标衡量原则。在精度指标调整与分配中,横向和纵向偏差系数需要分别进行调整与分配,以达到总体部门的要求。
下面就上述两种精度指标情况展开分析。
2.1 基于CEP准则的精度指标调整与分配
在文献[9]和文献[10]中, 针对惯性导航系统给出了CEP的分段计算方法,如下
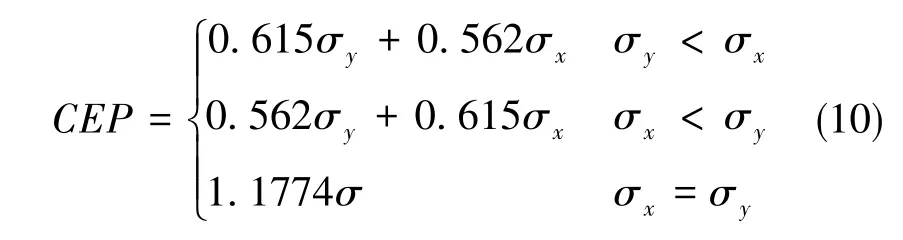
根据总体部门提出的圆概率误差要求值CEP0和环境函数,以及设计部门给出的惯性测量系统误差系数的初值解算出CEP值和各项误差系数的CEP值占比率,判定计算得到的CEP值与总体要求的CEP0大小。如果CEP0>CEP,则不需要调整惯性测量系统的误差系数;如果CEP0≤CEP,判断弹道导弹横向落点偏差和弹道导弹纵向落点偏差的大小。如果σL≥σH,解算出引起的横向落点偏差占比率最大的误差项,对其进行比例调整,调整后再进行CEP值计算,计算公式为CEP=0.615σH+0.562σL;如果σL<σH, 解算出引起的纵向落点偏差占比率最大的误差项,对其进行比例调整,调整后再进行CEP值计算,计算公式为CEP=0.615σL+0.562σH。
重复上述步骤直到计算出的CEP值小于总体部门给出的CEP值,此时的误差系数即为最终的满足总体部门要求的误差系数,上述步骤的设计流程图如图2所示。
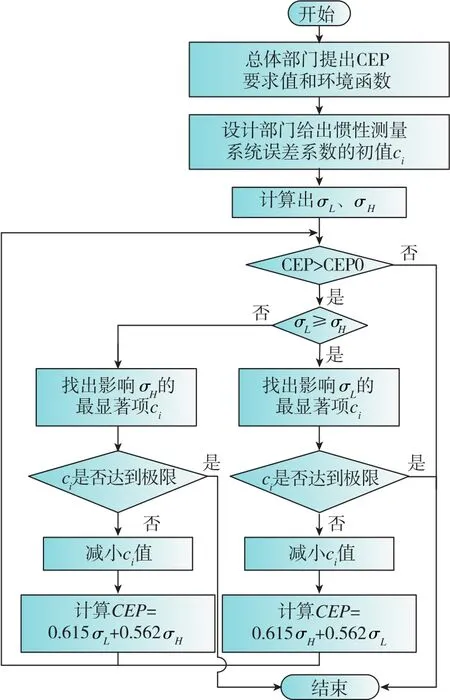
图2 基于圆概率误差的精度指标分配流程图Fig.2 Flowchart of error assessment based on the circular error probable
对圆概率误差下的精度指标调整过程进行仿真,取总体部门给出的环境函数和精度要求值以及设计部门给出的惯性测量系统误差系数初值为仿真数据,取调整因子为0.9,精度要求值CEP=3000m,计算得到的CEP初值为4926m。由图3可知,经过大约60次的调整,CEP值由4926m下降到2998m精度要求范围之内。最后,设计部门根据得到的最优误差系数对惯性器件进行进一步优化与调整。
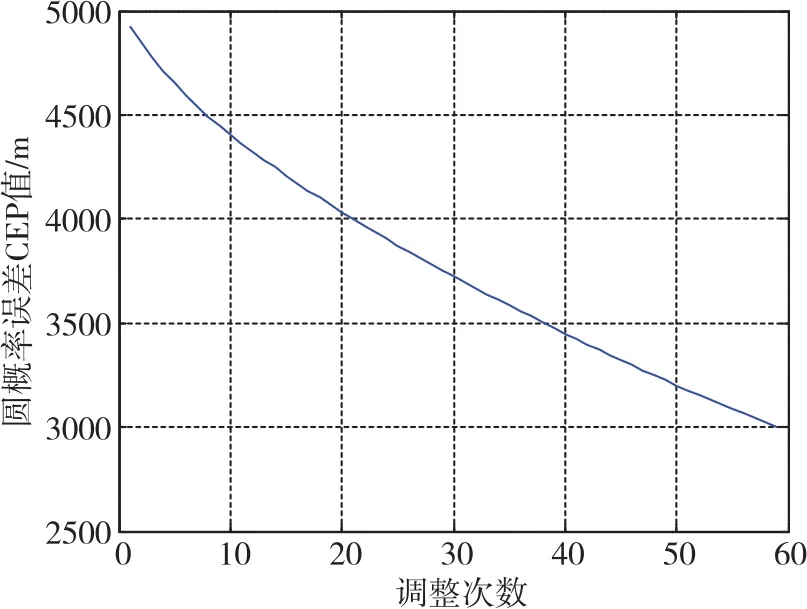
图3 圆概率误差CEP值随调整次数变化曲线Fig.3 Curve of CEP value with adjustment times
2.2 基于横纵向偏差较大时的精度指标调整与分配
基于CEP的精度评估准则,将落点横纵向误差近似折合成一维信息,没有分别对落点误差进行方向性分析,不能突出各项误差源分别对横纵方向的影响。因此,需要对横纵向精度指标分别进行调整与分配,并分析其各自的误差源。总体流程和基于CEP精度指标的情况相似,在给定的横纵向误差要求值的基础上分别对两个方向的误差系数进行调整,具体步骤如下:
1)首先比较计算出的横向、纵向位置偏差值σH、σL与总体部门给出的要求值σH0、σL0:
如果σL<σL0且σH<σH0, 则不需要调整惯性测量系统的误差系数;
如果σL>σL0或σH>σH0, 则分别判断弹道导弹横向落点偏差和弹道导弹纵向落点偏差与总体部门给出的要求值的大小。若σL>σL0, 解算出引起的横向落点偏差占比率最大的误差项,对其误差系数进行调整,调整后再进行横向落点偏差计算,得到一个新的σL;若σH>σH0, 解算出引起的纵向落点偏差占比率最大的误差项,对其误差系数进行调整,调整后再进行纵向落点标准差计算,得到一个新的σH。
2)重复上述步骤直到计算出的横纵向偏差值小于总体部门给出的要求值,此时的误差系数即为最终的满足总体部门要求的误差系数[10]。
图4为上述步骤的设计流程图。

图4 横纵向误差不等时精度指标分配流程图Fig.4 Flowchart of error assessment with unequal horizontal and longitudinal errors
取某弹道导弹环境函数和精度要求值(纵向为3000m,横向为1500m)以及设计部门给出的惯性测量系统误差系数初值计算得到的偏差(δL=57260m、δH=9392m)为例,以图4为规则对横纵向位置偏差不等情形下的精度指标调整过程进行仿真。
很显然,现有的惯性测量系统误差系数分配下的误差总和不能满足其精度要求值时,就需要对误差系数进行适当的调整直到达到预定的要求值。这里就涉及到调整方法的选取,取调整因子为固定值,大小为0.9。由图5、图6可知,纵向偏差值经过约236次调整由57260m下降到3000m精度要求范围之内,横向偏差值经过约151次调整由9392m下降到1500m精度要求范围之内。

图5 纵向误差随调整次数变化曲线Fig.5 Curve of longitudinal error with adjustment times

图6 横向误差随调整次数变化曲线Fig.6 Curve of horizontal error with adjustment times
2.3 惯性测量系统误差系数自适应调整方法
从前面的分析过程可以看到,对误差系数的调整主要依靠个人主观对导弹弹道和惯性测量系统误差系数项的经验值依次进行调整。比如,调整因子之所以选取0.9,主要目的是观察其收敛过程,但缺点是收敛速度较慢且收敛误差较大。因此,需要寻找一种全自动、自适应的调节方法以快速最优求解误差系数。
本文提出了一种自适应精度指标调整分配方法,可根据给定的弹道、环境函数和基于圆概率误差或者基于横纵向误差准则的精度要求值自动解算得到惯性测量系统最优误差系数,具体计算方法如下

式(11)中,kl和kh为纵向和横向自适应调整因子,i为调整次数(i=1,2,3,…),σLi/σL0为每一次调整后的纵向误差值与纵向误差初值之比,σHi/σH0为每一次调整后的横向误差值与横向误差初值之比,c′i为调整后的误差系数值,ci为调整前的误差系数值。随着调整次数i的增加,kl和kh的值会随着调节过程的递增逐渐减小,最终趋于1,即停止调整。
仍取2.2节的示例初值,由图7和图8可知,经过约200次自适应调整,纵向调整因子精度达到10-8(量级),纵向调整因子kl由19.09逐渐趋近于1,纵向误差值δL由初始的57260m逐渐趋于3000m,达到纵向误差精度要求;横向调整因子精度也达到10-8(量级),横向调整因子kh由6.262逐渐趋近于1,横向误差值δH由初始的9392m逐渐趋于1500m,达到横向误差精度要求。

图7 横纵向误差调整因子随调整次数变化的收敛曲线Fig.7 Convergence curves of horizontal and longitudinal factors varying with adjustment times
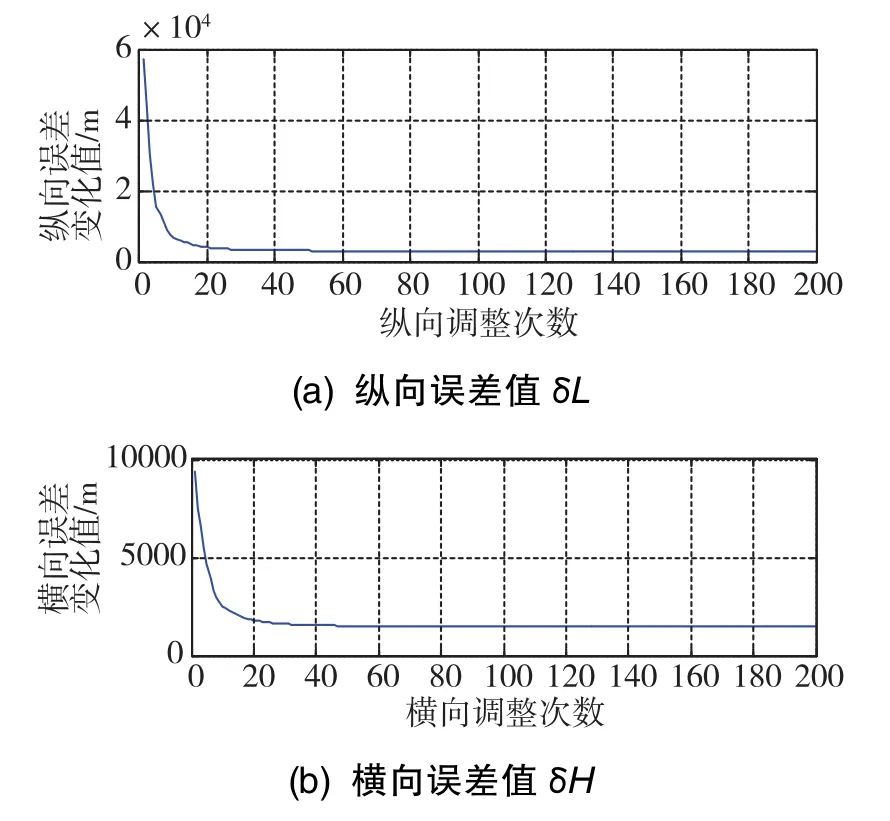
图8 横纵向误差值随调整次数变化的收敛曲线Fig.8 Convergence curves of horizontal and longitudinal errors varying with adjustment times
相比于图5和图6的固定比例调整过程,自适应调整方法以误差初值与误差要求值的占比为调整依据,并且随着调整次数的增加,调整因子会随着误差系数占比情况的减小而动态减小,直到调整因子趋于1,调整饱和,惯性测量系统的误差系数达到最优。
3 仿真验证与结果分析
误差分配的关键是误差分配原则的选取,即将总误差在引起总误差的误差源之间进行合理的平衡。以下分别以CEP值和横向、纵向精度要求值为精度指标,仿真验证了弹道导弹惯性测量系统精度指标分配的结果,并对精度指标分配方式进行客观总结。
3.1 基于CEP准则的实验仿真分析
采用自适应的精度指标调整方法对基于CEP评估准则的弹道导弹惯性测量系统进行精度指标分配的仿真验证,已知环境函数和惯性测量系统误差系数初值,精度要求值CEP=3000m。图9和图10分别给出了调整前、调整后最优误差系数下的导弹落点分布和CEP模型。模拟打靶1000发,初始误差系数下的CEP值约为4926m;调整后最优误差系数下的CEP值达到精度指标要求3000m。由图11可知,以自适应精度指标分配的方式对误差系数进行调整,调整后的主要误差系数项的占比基本趋于均匀,约占10%~12%。相比于图1差距较大的占比情况,自适应精度调整方法更有利于对惯性测量系统进行后续的优化、改进和误差补偿等工程实现,在实际设计中更加具有实际指导意义。

图9 调整前的CEP模型Fig.9 Diagram of CEP model before adjustment
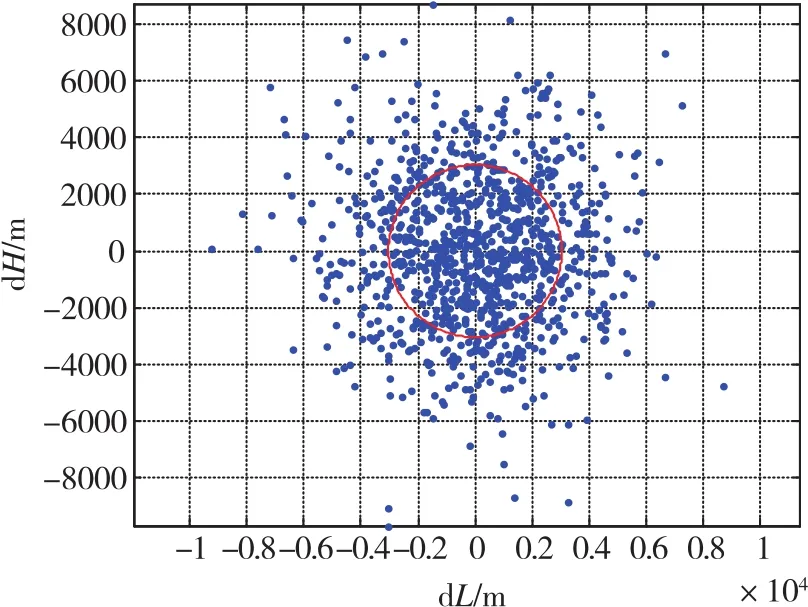
图10 调整后的CEP模型Fig.10 Diagram of CEP model after adjustment
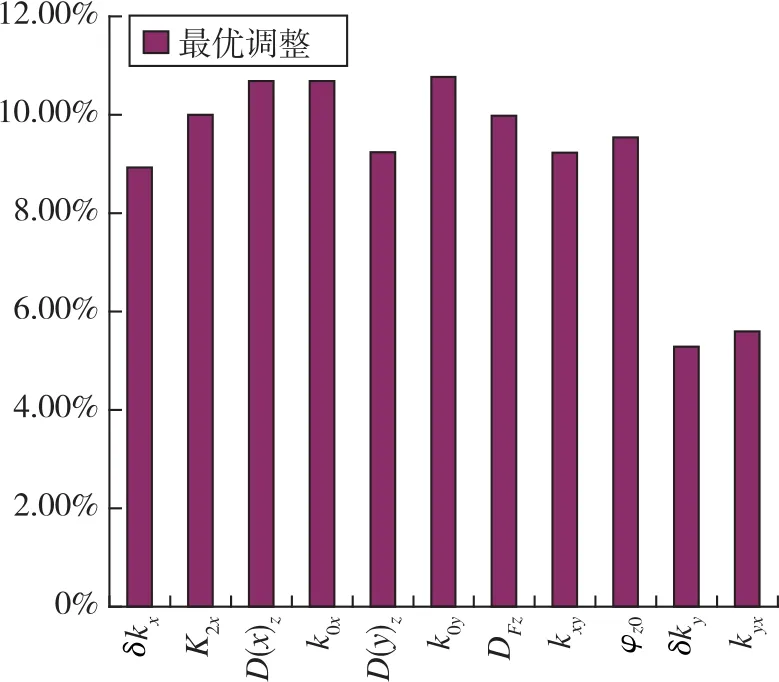
图11 调整后各误差源的占比分布Fig.11 Navigation errors ratio of each instrumental error after adjustment
3.2 基于横纵向误差准则的实验仿真分析
以图1所示的误差系数初值为例,图12给出了自适应调整之前的导弹落点分布和EEP模型。

图12 调整前的EEP模型Fig.12 Diagram of EEP model before adjustment
由图12可知,该弹道导弹不能满足精度要求值ΔL=3000m、ΔH=1500m。因此,采用自适应的精度指标调整方法对基于横纵向误差评估准则的弹道导弹惯性测量系统进行精度指标分配仿真验证。通过自适应精度指标分配的方式对误差系数进行调整,调整后的主要误差系数项的占比基本趋于均匀,约占20%,如图13和图14所示。
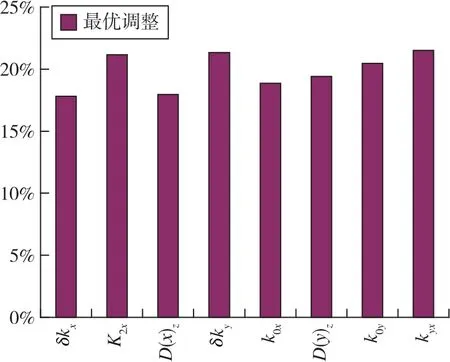
图13 调整后各误差源在横向的占比分布Fig.13 Navigation errors ratio of each instrumental error after adjustment in horizontal direction
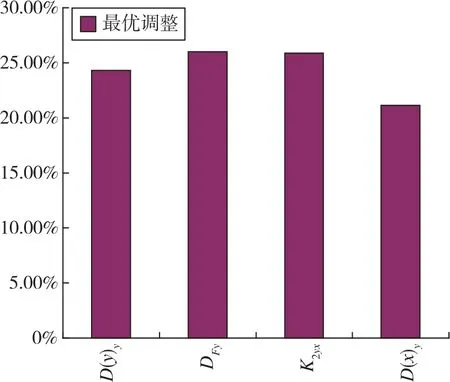
图14 调整后各误差源在纵向的占比分布Fig.14 Navigation errors ratio of each instrumental error after adjustment in longitudinal direction
图15给出了自适应调整之后的导弹落点分布和EEP模型。
图12与图15对比可知,调整后的纵向误差值由初始的57260m降至3000m左右,横向误差值由初始的9392m降至1500m左右,具体值为σL=3015.1726m和σH=1489.3341m。
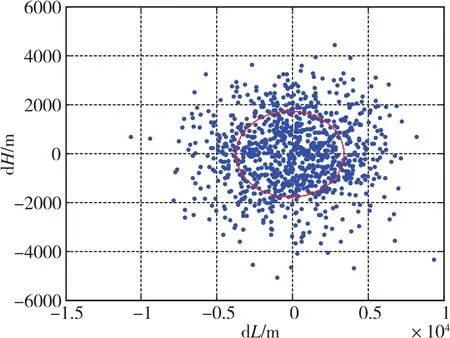
图15 横纵向位置偏差不等情况下的落点分布和EEP模型Fig.15 Diagram of fall point distribution and EEP model with unequal horizontal and longitudinal errors
以上分别给出了CEP=3000m及横向、纵向误差分别为1500m、3000m情况下的仿真结果。在实际仿真中,利用本文提出的一种惯性测量系统动态自适应精度指标调整方法可以对任意精度要求的误差系数进行自适应调整和精度指标分配,即实现动态精度下的精度指标自动分配。
但需要注意的是,上述惯性测量系统精度指标自适应分配结果只是理论层面和基于惯性测量系统层面的参考结果。在实际应用中,需要考虑实际生产水平中能达到的惯性器件精度条件,还需要考虑除惯性器件外的其他影响精度的因素以及生产效益、经济允许能力、研制时间周期等限制条件。
4 结论
本文针对目前弹道导弹惯性测量系统精度指标分配方法存在的缺点,对惯性测量系统的误差分析、误差调整和分配方法做了更加完善、创新的研究。通过对惯性测量系统误差源的全面分析,提出了一种弹道导弹惯性测量系统精度指标自适应分配方法,该方法能够根据不同精度要求实现基于动态的自适应方法的精度误差指标调整和分配。在此基础上,还提出了一种在横向、纵向落点偏差不等时的精度指标分配方法,分别得到了影响横向、纵向误差的误差源和横纵两个方向上惯性测量系统最优误差系数。最后,通过仿真验证了提出的自适应精度分配方法的正确性和合理性,对实际武器导航系统研究设计具有一定的指导意义和设计参考价值。

