光纤陀螺惯性平台的稳定回路控制
徐白描,魏宗康,彭 迪
(北京航天控制仪器研究所,北京100039)
0 引言
陀螺惯性稳定平台系统是以陀螺作为敏感元件,通过稳定回路实时测量和调整平台台体的姿态从而隔离载体角运动,以便为加速度计提供一个良好的工作环境,高精度惯性稳定平台系统对于提高军事化武器在目标打击过程中的命中率与命中精度至关重要[1-2]。
液浮陀螺、挠性陀螺目前已具备了较成熟的技术,现有的惯性稳定平台系统多采用气浮陀螺、液浮陀螺或挠性陀螺作为敏感元件,但由于工艺、成本以及对军事化打击更高的精度要求等因素正逐渐被新型陀螺所取代。光纤陀螺是全固态光学陀螺,具有结构简单、精度覆盖面广、可靠性高以及使用寿命长的优势。因此,国外的光纤陀螺稳定平台已经成功应用于武器系统中,我国对于光纤陀螺惯性稳定平台的研究也日益重视。目前,国内多个科研院所都已开展了光纤陀螺稳定平台的研发,其中对基于光纤陀螺的平台稳定回路成为了研究重点。2007年,第二炮兵工程学院的周小刚等[3]提出了光纤陀螺惯性平台稳定系统的设计方案。2016年,中国北方车辆研究所的刘义等[4]采用光纤陀螺替代挠性陀螺建立了惯性平台稳定回路模型,并采用经典PID控制算法仿真验证了光纤陀螺的可行性。这两篇文章都没有对控制器设计过程进行详细的介绍,仅给出了设计结果。2015年,天津航海仪器研究所的毋兴涛等[5]对由光纤陀螺构成的惯性稳定回路进行了关键技术分析,设计了串联超前-滞后校正网络,控制器的设计方法主要是根据经验调节PID参数,运算量较大,并且对平台稳定回路设计指标中的动态指标考虑不全面。以上研究对于光纤陀螺稳定回路设计具有借鉴意义,但也存在一定的局限性,比如没有考虑光纤陀螺的滞后环节对稳定回路的相位影响,设计方法严重依赖于人的经验知识等。
因此,本文提出了基于H∞控制理论的控制器设计方法,该方法可在性能指标的限制条件下基于计算机软件程序快速解出控制器。基于该控制器,本文给出了基于光纤陀螺的平台稳定回路仿真结果以及实际试验对所设计控制器的验证。
1 光纤陀螺惯性平台稳定回路建模
以单条回路为例,构成稳定回路的主要部分为敏感元件、控制器、执行机构和稳定对象等。当有干扰力矩Mf作用在框架轴上时,台体相对惯性空间发生转动。相应地,光纤陀螺就会敏感到该转动角速度,并输出对应的信号经功率放大器输出后驱动直流力矩电机,产生电机力矩抵消框架轴上的干扰力矩Mf,使平台稳定在惯性空间。根据这个过程,给出的平台系统稳定回路框图如图1所示[6-7]。
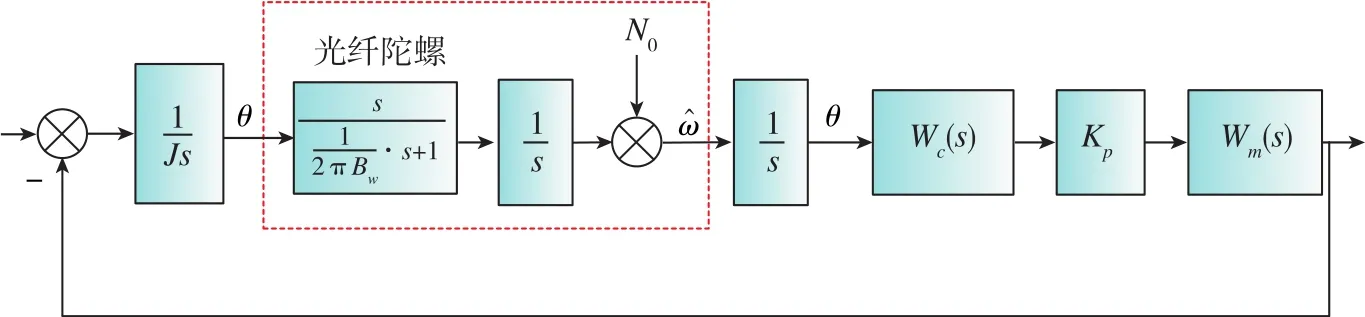
图1 光纤陀螺稳定回路框图Fig.1 Block diagram of fiber optic gyroscope stable loop
光纤陀螺的传递函数为

式(1)中,KD为直流增益,Bw为频带宽度,Td为延迟时间。
光纤陀螺传递函数的形式可描述为一阶惯性环节、延迟环节、比例环节的串联,三个环节对稳定回路系统开环传递函数频率特性的影响如图2所示。
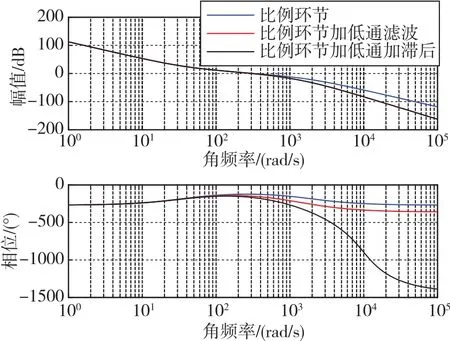
图2 各环节对幅频特性的影响Fig.2 Effects of various links on amplitude-frequency characteristics
如图2所示,延迟环节不改变幅值特性,红线与黑线重合,只在相频特性中有明显的相位延迟现象。为分析方便,控制器设计时暂不考虑延迟环节。根据图1中伺服回路系统计算得到的开环传递函数为
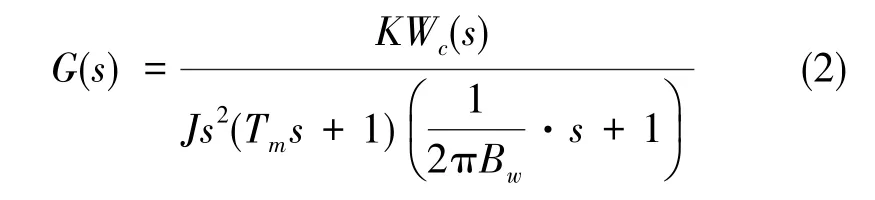
将各项参数带入未加以校正的系统,得到的开环Bode图如图3所示。
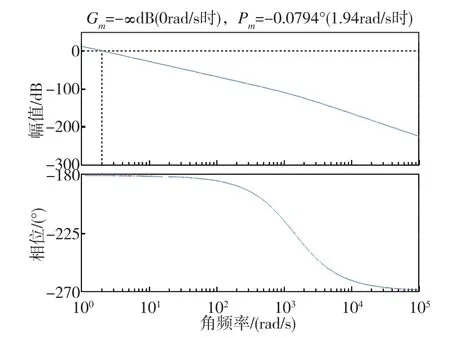
图3 未校正系统的开环Bode图Fig.3 Open loop Bode diagram of uncorrected system
如图3所示,未加入校正装置前,开环系统的截止频率ωc=1.94rad/s,相位裕度γ=-0.0794°,幅值裕度为负无穷大,以上三项频域指标均不满足要求。为了得到稳定、角度无静差的系统,需要设计校正环节对系统进行校正。
2 H∞控制器设计
本次控制器设计的性能指标要求为:2000g·cm常值干扰力矩作用下,平台的角度静差≤10″;在幅值为600g·cm、频率为1Hz的正弦干扰力矩作用下,角度小于30″;回路调节时间小于0.1s;幅值裕度大于8dB,相角裕度大于25°。平台稳定回路的框图如图4所示。

图4 约束条件下的光纤陀螺稳定回路框图Fig.4 Block diagram of fiber optic gyroscope stable loop under constraint conditions
图4中,W1(s)和W2(s)分别为性能界函数和对象不确定性界函数;u为控制的输入信号,是被控对象的输入信号;y为反馈量,是被控对象的输出量;r为校正环节输入端信号,n为干扰信号,z为评价信号。 设控制器C(s)=KWc(s), 被控制对象可求得
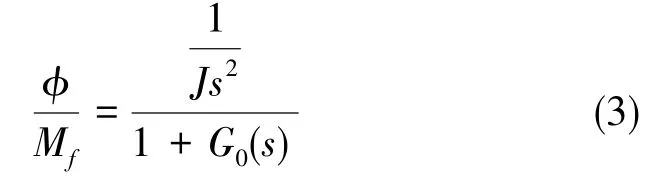
式(3)中,G0(s)为系统开环传递函数。
在幅值为6°、频率为1Hz下的要求为

考虑系统的输入和输出关系以及误差信号,有
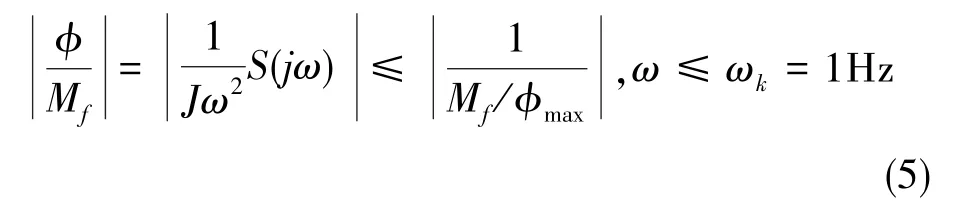
式(5)中,S(jω)为系统的灵敏度函数。 灵敏度函数是决定跟踪误差大小最重要的指标,当灵敏度函数的奇异值越低,则系统的跟踪误差越小,也即对干扰的抑制能力越强。令它可同时满足动静态指标[10-11],则灵敏度函数为
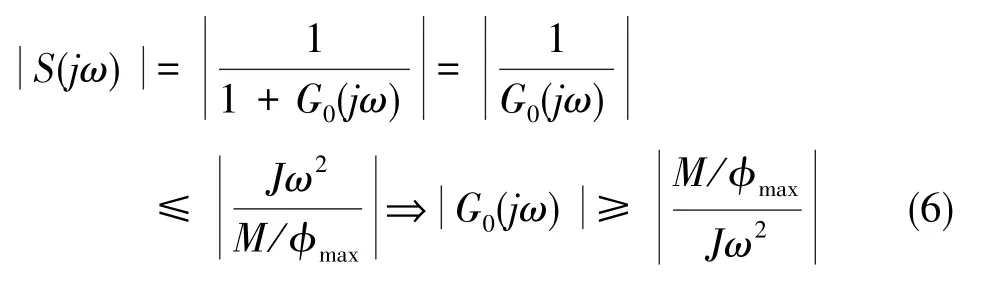
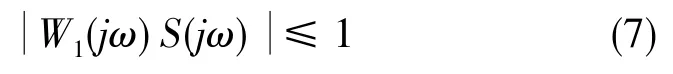
那么,它的性能指标为





校正后的系统开环传递函数Bode图如图5所示,滞后环节不影响幅值特性,但会影响相位。由图5(a)可知, 剪切频率为ωc=163.07rad/s。 由图5(b)可知,未考虑滞后环节时,系统的相角裕度为53.96°,幅值裕度为22dB;考虑滞后环节时,系统相角裕度为44°,幅值裕度为14.9dB。可以得出,所设计的控制器仍然满足精度和鲁棒稳定性。

图5 系统开环传递函数Bode图Fig.5 Bode diagram of system open loop transfer function
3 试验结果及分析
3.1 仿真验证
1)单位阶跃仿真验证
为验证控制器的性能,对平台稳定回路进行单位阶跃响应仿真,结果如图6所示。
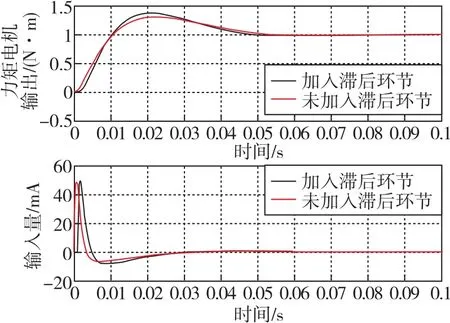
图6 稳定回路单位阶跃响应Fig.6 Diagram of stable loop step response
由图6可知,加入滞后环节后,系统响应存在1ms的时间延迟,超调量有所增加。
2)正弦仿真验证
为验证稳定回路在动态条件下的性能,对框架加入幅值为600g·cm、频率为1Hz的正弦干扰力矩进行仿真,如图7所示。由图7可知,框架轴转动角度为1.07″,小于30″,稳定回路的设计满足动态性能指标要求。
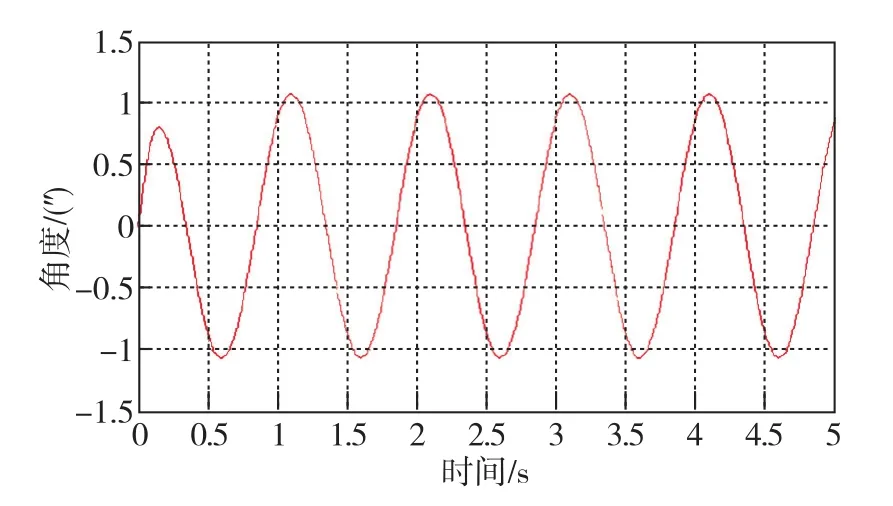
图7 正弦干扰力矩下框架角的输出Fig.7 Output of frame angle under sinusoidal interference torque
3.2 闭合试验
对光纤陀螺稳定平台进行单通道闭环试验。图8为光纤陀螺采集到的闭合前后的数据,采样时间为5ms,采集时长2min。可以看出,在平台上电10s后对平台进行闭合,稳定回路快速回到零位,此时陀螺输出均值为零。
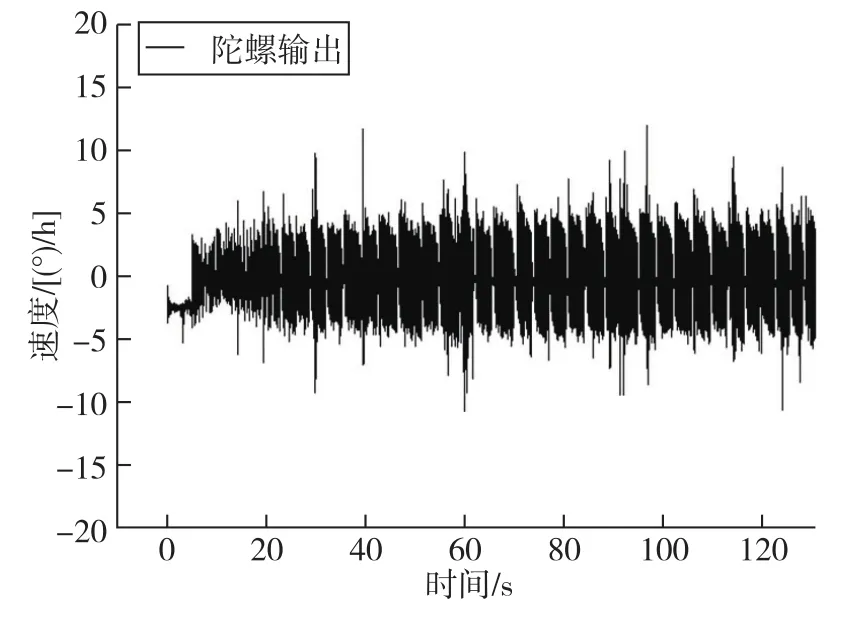
图8 光纤陀螺的输出信号Fig.8 Output of fiber optic gyroscope
虽然平台稳定回路闭合正常,但可以看出光纤陀螺的输出噪声较大,瞬时幅值可达10(°)/h。为分析噪声原因,利用Allan方差对陀螺闭合后的输出信号进行分析。图9为噪声信号的功率谱密度曲线,图10为对噪声信号计算Allan方差得到的标准差-相关时间双对数曲线。

图9 功率谱密度分析Fig.9 Diagram of power spectral density analysis

图10 光纤陀螺的Allan方差图Fig.10 Allan variance diagram of fiber optic gyroscope
由图9可知,陀螺噪声信号在16Hz左右幅值最大,随后出现衰减,与系统所设计的转折点位置相符。图10中的Allan方差分析结果表明,对于该光纤陀螺,其量化噪声为主要噪声源,由于采样时间太短,计算结果中没有反映出零偏不稳定性的估计结果。 在相关时间为 5×10-3s~2×10-2s内,曲线有一段斜率为零的线段,这并不是零偏不稳定性的估计结果。
4 结论
本文重点分析和研究了以光纤陀螺作为传感器的惯性平台稳定回路控制技术。根据动静态指标及裕度指标,基于H∞控制理论对某型号光纤陀螺惯性平台进行稳定回路设计,通过仿真验证了稳定回路的性能。同时,为了验证滞后环节对稳定回路性能的影响,在仿真时考虑了光纤陀螺的滞后环节。结果证明,加入滞后环节会造成相位延迟,但是所设计的稳定回路仍然可以满足性能指标,说明控制器具有较好的鲁棒性。最后进行了稳定回路闭合试验,利用Allan方差法对稳定回路闭合后的光纤陀螺输出噪声进行了分析,分离出光纤陀螺信号中的主要随机误差,验证了控制器的正确性。

