基于灰度共生矩阵和同步正交匹配追踪的分形图像压缩

杨蒙蒙，张爱华

（南京邮电大学理学院，南京 210023）

（*通信作者电子邮箱zhangah@njupt.edu.cn）

0 引言

随着多媒体信息以及计算机工业技术的高速发展，分形图像压缩编码算法作为一种与时俱进、功能强大的图像压缩技术，利用图像内部的自相似性以及各个区域之间可以相互表达的特性，成为有损压缩图像技术的代表。它由Barnsley［1］于1988 年提出最初的思想，Jacquin［2］在原有的基础上进行改进从而发展起来，基于分形的图像压缩编码其压缩方法简单，可在任意尺度下重构且压缩比高具有独特优势，但是与传统的图像编码技术相比，在灰度匹配过程中由于需要大量的相似性计算，因此非常耗时［3］。在过去的时间里，为了降低计算成本，研究者们进行了许多有效的研究［4-21］，从空间关系［4-6］的角度出发、采用邻域方法、缩小匹配图像块大部分相邻的搜索空间。从平面拟合的角度出发，Lu 等［7］提出了一种新的基于Huber 拟合平面鲁棒分形图像编码，与Shen 等［8］的无搜索方法相比，在稳健回归模型中建立新的灰度匹配，引入一种新的匹配误差函数，降低了计算量；对于典型的优化算法，Wang等［9］提出了一种将粒子群优化（Particle Swarm Optimization，PSO）算法和混合四叉树划分相结合的分形图像编码算法，采用基于范围块分类的PSO 搜索策略，在缩短编码时间的同时改善了重建图像质量。从参数变换和相关系数出发，利用相邻像素间的相关性，将问题由图像域转换到向量域，降低了合适域搜索的复杂性［10-12］，例如Maydaniuk 等［12］提出了一种基于二维线性近似系数表示范围块和域块的方法，允许每个范围块通过三个近似系数对块进行快速预选来缩短编码时间。此外，基于特征向量法，何传江等［13］提出的改进分形叉迹算法以及张璟等［14］提出的双交叉和特征算法都在一定程度上缩短了编码时间。

为了更进一步平衡编码时间和图像重构质量的关系，本文将提取图像的灰度共生矩阵作为特征向量，进行相似性计算来缩减码本，通过灰度稀疏匹配追踪变换和特征提取之间建立密切的关系，获得了更好的解码质量和更快的编码速度。

1 基本分形编码算法

在分形压缩编码算法中，原始图像被划分成大小为r×r的不重叠范围块Ri(i=1，2，…，N)，以及可以重叠且大小为d×d的域块Dj(j=1，2，…，M)，其中，域块的大小一般取范围块大小的两倍，即d=2r。在编码过程中，通过空间压缩［2］将定义域块D的大小降至范围块R的相同大小［15］，所有收缩后的D块经过8 个等距变换后形成虚拟码本，因此变换后的域块D和范围块R之间的灰度变换可以表示为：

同时在编码过程中，为了寻求R块的最佳匹配块，需满足匹配误差最小［2］，即：

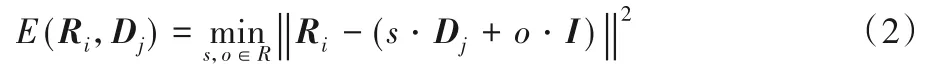
其中：‖‖· 表示l2范数，I是亮度值均为1 的常值块，s和o分别起调整Dj的对比度和亮度的作用，通过最小二乘法求解式（2），得到最小平方问题的解：

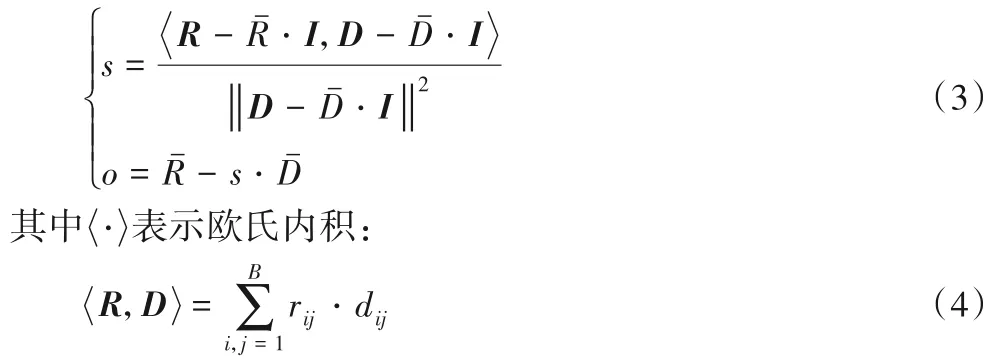
R、、D和分别表示为图像块R和D的像素灰度值用某种扫描方式所构成的向量及其均值。经过上述求解后，得到R的分形码，即域块D的位置、等距变换t、对比度参数s和亮度偏移参数o。详细的块匹配过程如图1 所示，全体R块分形码构成了原始图像的分形码，描述了一个使原图像近似不变的压缩变换；解码过程是一个相对简单的迭代过程，基于压缩不动点定理和分形编码，解码过程从任意图像开始，最后，迭代吸引子［2］便是原始图像的一个近似图像。

图1 范围块和域块之间的收缩仿射变换过程Fig.1 Process of compressive affine transformation between range block and domain block

2 基于灰度共生矩阵的正交化稀疏编码

2.1 特征提取和图像块检索

灰度共生矩阵是1973年由Haralick等［16］提出的一种通过研究灰度的空间相关特性来描述纹理的常用方法。作为一种成熟的统计图像分析方法，灰度共生矩阵［17］具有较强的适应性与鲁棒性，且方法简单，在统计分析领域应用较广。通过计算灰度图像得到它的共生矩阵，然后通过计算该共生矩阵得到矩阵的部分特征值来分别代表图像的某些纹理特征［18］。在本文中，使用对比度、能量、熵、相关性4 个特征来进行图像块的检索，公式如下：

1）能量（Angular second moment，Asm）。

2）熵（Entropy，Ent）。

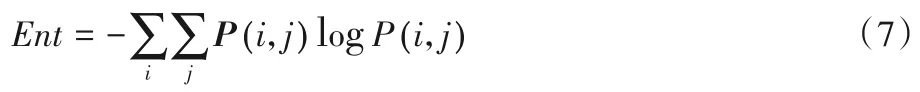
3）对比度（Contrast，Con）。

4）相关性（Correlation，Corr）。

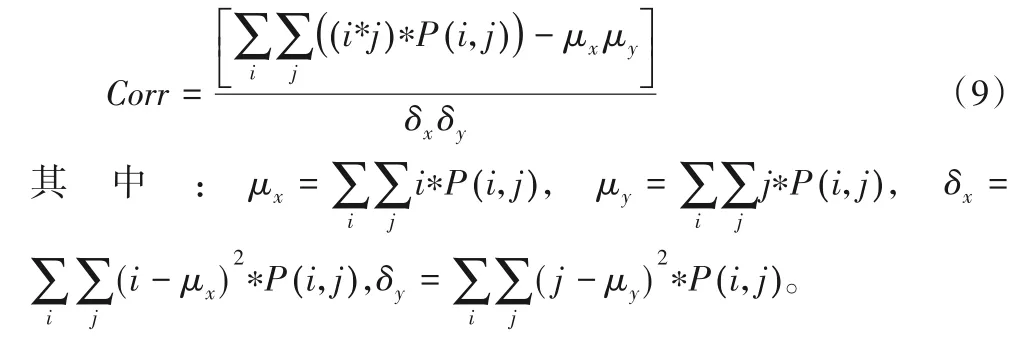
分别对R块和D块提取以上4 个特征，为了方便计算，本文将能量、熵、对比度和相关性的均值作为最终的纹理特征，且均值特征向量使用T=[T1T2T3T4]来表示，对于每个R块和所有D块之间的相似性匹配d(TRi，TDj)，根据实验效果采用切比雪夫距离进行衡量，即dist(Ri，Dj)=，当检索码本中的D块时，较短的距离表示纹理相似度较高，d(TR，TD)之间的距离越小，则证明R块和D块越匹配，因此将R块和所有D块之间的切比雪夫距离由小及大排序，得到关于块R的相似度量矩阵Δ(Ri，Dj)=这种方法可以快速提取图像块之间的相似度信息，降低计算的复杂度，在改善重建图像质量的基础上加快编码速度。

2.2 SOMP稀疏分解思想

基于正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法，同步正交匹配追踪（Simultaneous Orthogonal Matching Pursuit，SOMP）算法［19］同样也是一种贪婪追踪类算法，顾名思义，SOMP 能够同时进行稀疏逼近。一般来说，信号在其稀疏域越稀疏，其信号重建就越准确，对于图像而言，本身具有较复杂的特征，由此学者们提出了使用超完备冗余字典［20］来对信号进行稀疏表示。

从理论上讲，字典Q中的每一列是一个训练样本，测试样本x∈Rd为一个列向量，它们的关系表达如下：

其中Si∈Rn为qi的表示系数，方便叙述，式（10）简化为：

其中矩阵Q=[q1，q2，…，qn] ∈Rd×n是一个基矩阵，但式（11）是欠定线性组，因此它的解答可以等价为求解l1范数的稀疏最优解过程，如下：

在保证重构精度的前提下，求解出尽量稀疏的系数矩阵S。

2.3 正交化稀疏灰度匹配变换

在基本分形编码过程中，范围块R作为待编码的块，域块D作为码字。对于每个范围块，在域池中搜索匹配一对一的域块。通过实验发现对于一些结构相似度低的图像，如果图像的域块不能很好地逼近距离块，这种方法不仅耗时而且重构图像质量较低［21］，无法满足实际需求。在本文中，为了使R块尽可能匹配更多的域块D，此次将SOMP算法应用到块的匹配过程，通过生成相应的稀疏系数矩阵S，实现了一个范围块和多个域块之间的匹配关系。

2.3.1 确定过完备虚拟码本

作为一个虚拟码本，域池中通常包含大量的域块，这些块D={dj}Ω可以作为稀疏编码的过完备基集，做规范化处理后，R块和D块的匹配过程是在域池中为每个R块搜索相应的基，因此可以直接将稀疏编码的搜索策略应用到分形中［22］。

2.3.2 正交化分形编码

由BFIC（Baseline Fractal Image Compression）的具体流程可知，对比度参数s和亮度偏移参数o的值依赖于块Di，相关的编码参数在具体的迭代过程会发生变化，这种变化带来的不确定性不利于分形编码参数进行块与块之间的匹配，本文采用正交分形编码算法［23］保证参数在迭代过程的稳定性。因此由=0，则有：

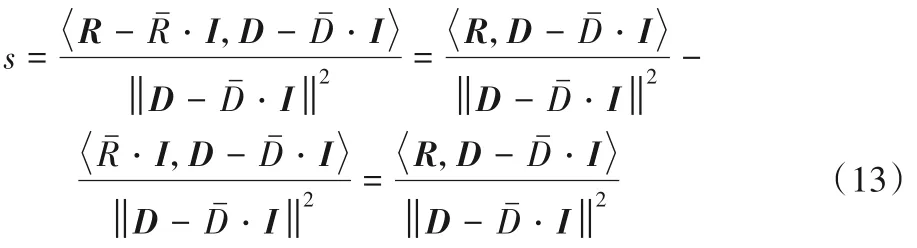
由于从D块到R块的仿射变换是由参数s和Rˉ决定的，因此这两种参数的联合统计特征能有效表征仿射变换的统计特征［24］。

2.3.3 稀疏灰度匹配

基于构造的过完备虚拟码本，由稀疏分解的思想，所谓的匹配即为求解相应的稀疏系数矩阵的过程，假设为每个R块匹配域池中的k个块Di(i=1，2，…，k)，每个域块的线性系数分别为s1，s2，…，sk，根据稀疏分解，定义一种新的灰度变换为：

其中：R和为图像块R的像素值和均值，si(i=1，2，…，k)为对比度参数，且，根据上述灰度变换，在对每一个块R编码的情况下，由式（13）表示的结构存储分形码表示如下：

2.4 算法描述

基于以上分析，算法具体实现步骤如下。

1）图像分割。将大小为N×N的原始图像μorg分割成互不重叠的大小为8× 8 的R块集合，以纵横方向步长δ=8 生成可重叠且大小为16 × 16的D块集合。

2）特征提取。分别对R块和等距变换后的D块进行灰度共生矩阵的纹理特征提取。

3）码本构成。根据提出的相似性度量矩阵，计算同等条件下R块和D块的切比雪夫距离，由小及大排序记为Δ(R，D)。

4）虚拟码本。取前M个距离较小的D块，进行规范化处理后引入8种等距变换，构成缩减后的过完备虚拟码本

5）使用SOMP正交化分形算法灰度匹配：

3 实验结果及分析

为了测试本文算法的有效性，选取了5幅大小为512像素×512 像素的标准灰度图像进行实验，分别为Lena、Elain、Peppers、Goldhill 以及Zelda，硬件平台为Window 10 和CPU Ryzen5-2500操作系统的计算机，所有方法均在Matlab2018a环境中实现，对比参数为编码时间、峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）和结构相似度（Structural SIMilarity，SSIM）。

3.1 实验参数设置

在本文算法中，编码时间和图像重构质量依赖于两个控制参数：稀疏度L和所提取的特征数量M，由2.1 节的分析可知，M的大小决定了过完备虚拟码本的大小，M值越大，匹配块的空间大，图像重建质量较好，但也伴随着一定数量的数据冗余，因此，设置合理的码本数量对编码的质量和速度至关重要，如图2～3 所示，当M的值为250 时，PSNR 的增长趋于平缓且编码时间急剧增长，因此M的取值范围控制在M∈（0，250）比较合适，经过实验对比分析，在保持实验效果和时间平衡关系的前提下，本文取M=250。

图2 特征数量M和PSNR关系Fig.2 Relationship between the number of features M and PSNR

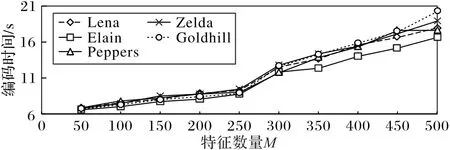
图3 特征数量M和编码时间的关系Fig.3 Relationship between the number of features M and encoding time

稀疏度L作用于迭代过程的终止以及相应的重建效果，如图4 和图5 所示，L值越大，图像的PSNR 越高，但同时也伴随着较长的编码时间。当L在8～10 时，曲线增长较为平缓且PSNR 也在可接受范围内，综合考虑这两个因素，根据算法的时效性，本文中稀疏度L取9比较合适。

图4 稀疏度L和PSNR关系Fig.4 Relationship between sparsity L and PSNR

图5 稀疏度L和编码时间关系Fig.5 Relationship between sparsity L and encoding time

3.2 实验结果与分析

本文选取基本分形算法（BFIC）、改进分形编码的叉迹算法［13］、双交叉和特征算法［14］和稀疏分形图像压缩（Sparse Fractal Image Compression，SFIC）算法［22］与本文算法进行比较，为了保证算法的公平性，取相同尺度参数，重构误差阈值设置为20，图6 为几种算法编码的解码图像对比。与BFIC 算法、改进叉迹分形算法以及双交叉和特征算法相比，从Lena放大的局部图像来看，前三种算法的重构图像都出现了明显的块效应，而在Goldhill 解码图像中，这三种算法在关于天空的细节上也有缺陷，本该灰色天空的地方出现了泛白的迹象，本文算法在视觉效果上几乎与原图没有差别，获得了高质量重建图像的同时编码速度也得到了较大的提升。根据表1 可知，实验数据变化最大的是图像Peppers，在双交叉和特征算法中，PSNR 仅为9.33，在本文算法中，获得了较好编码质量的同时编码时间也大大缩短，虽然和SFIC 算法相比，图像Lena 和Goldhill 的PSNR 稍低了一点，但在保证一定图像质量和结构相似度（SSIM）的前提下，编码耗时缩短了至少89%。

图6 不同算法的解码效果Fig.6 Imag decoding effects of different algorithms

表1 测试图像在不同算法下的性能Tab.1 Test image performance under different algorithms

图7 进一步表明本文算法在编码效率上的优化，因此综合比较得知，本文的算法可以获得较好的重建质量同时保持更快的编码速度，较相应的对比算法更有效。

图7 测试图像在不同算法下的编码时间对比Fig.7 Comparison of encoding time of test images under different algorithms

4 结语

针对传统分形图像压缩中存在的计算复杂度高问题，本文提出了一种基于灰度共生矩阵纹理特征的正交化分形编码算法，将相似性度量矩阵关于图像检索的概念引入分形图像压缩，有效减少了搜索空间，和SOMP 算法相结合的灰度匹配更是提高了重建的图像质量，编码速度也得到了较好的提升，通过实验证明了本文算法的有效性。

图像压缩编码作为人工智能时代通信技术的一个重要应用，减少图像数据中的冗余信息，使用更加高效的格式存储以及传输数据是十分必要的。本文算法在时间效能上还有待提高，因此接下来将尝试使用智能优化的算法来加快图像块之间的匹配搜索，从而把构造效果更佳的混和编码算法作为接下来的重点研究方向。