基于住户差异性的住宅建筑在室行为预测模型
俞准 刘竹清 李郡 周亚苹 黄余建 张国强


摘 要:现有住宅建筑在室行为预测模型缺乏对住户差异性的合理考虑,导致模型往往存在整体预测精度不高和适用性受限等问题. 针对这一问题,提出一种考虑住户差异性的马尔可夫链在室状态预测模型. 该模型首先通过Spearman相关性分析确定了不同影响因素(即特征参数)与住户总在室时长的相关性,将相关系数作为特征参数权值并结合聚类分析对住户群体进行分类. 在此基础上采用马尔可夫链模型对住户在室状态进行预测. 为评估所建立预测模型的性能,以英国TUS(Time Use Survey)数据库为例,将改进模型与传统马尔可夫链模型进行对比分析. 结果表明,该方法能够综合考虑不同住户特征参数及其对在室行为的影响,对住户进行合理的分类,与传统马尔可夫模型相比,所建预测模型显著提升了整体性能,平均绝对误差和均方根误差分别减小了20.57%和15.35%.
关键词:在室行为;住户差异;相关性分析;聚类分析;马尔可夫链模型
中图分类号:T111.1 文献标志码:A
Abstract:Existing occupancy prediction models for residential buildings often lack the reasonable consideration of resident diversity, which generally results in poor prediction accuracy and limited applicability. To address this issue, this study proposes a Resident-differentiated, Markov Chain Occupancy Prediction Model with Cluster (RMCPMC) analysis to fully consider the resident diversity so as to improve the model predictive performance. First, Spearman correlation analysis is employed to identify the correlation between different influencing factors (i.e. resident characteristics) and total occupancy duration. The identified correlation coefficients are used as the weights for corresponding factors, and cluster analysis is subsequently performed to classify residents into different groups. Finally, RMCPMC models are established for obtained clusters to predict the occupancy pattern. To validate the performance of the proposed model, it is applied to the UK Time Use Survey (TUS) dataset and its performance is compared with the conventional Markov Chain(MC) model. Compared with the conventional MC model, the Mean Absolute Error and the Root Mean Square Error of the prediction accuracy decrease by 20.57% and 15.35%, respectively. The results indicate a significant improvement in model prediction accuracy through reasonably considering resident diversity and their impacts on occupancy patterns.
Key words:occupancy;resident diversity;correlation analysis;cluster analysis;Markov chain model
建筑在室行為是影响建筑能耗的主要因素之一[1]. 就住宅建筑而言,研究表明对其住户的在室行为,尤其是在室状态(即居民是否在室),进行合理定量描述和准确长期预测,是提升建筑能耗预测和模拟精度的有效手段[2]. 现有住宅建筑在室状态预测模型主要包括统计概率模型、数据挖掘模型、马尔可夫链(Markov Chain,MC)模型和Agent-based模型,其中应用最为广泛的是马尔可夫链模型[3],该模型考虑了在室状态在时间上的关联性并能在一定程度上刻画建筑住户行为的随机性. 例如,Richardson等人[4]基于英国TUS数据库,分别针对工作日及非工作日建立MC模型以预测住户在室状态. 结果表明该方法可以较好地预测在室状态,但其局限性也较为明显,主要体现在该方法是对数据库中所有住户进行统一预测,忽略了不同住户之间的差异性. 考虑到不同特征住户的在室规律有所不同,该方法必然导致模型预测性能下降. 对此,有学者在对住户进行分类的基础上进行在室状态预测. 例如,Flett等人[5]首先选取部分住户特征参数对英国住宅进行分类,然后对不同类住户在室状态进行分别预测. 该方法可在有效降低计算量的同时提高模拟精度,但仍存在明显的局限性:一是所选取的住户特征参数受研究者自身经验和主观因素影响,容易忽略部分与在室行为相关的重要因素;二是没有考虑不同因素对住户在室行为的影响程度大小,限制了模型预测性能的提升. 此外,部分学者尝试采用无监督聚类分析方法从住户在室状态信息中直接获取不同住户群体[6],再对不同群体住户在室状态进行预测. 该方法可保证同一住户群体具有相似的在室作息规律,从而提升了模型预测性能,但由此获取的住户群体其社会经济背景等特征可能具有显著差异,导致在实际应用中对某一住户进行能耗模拟时难以确定该住户属于哪类群体,从而限制了该方法的实用性.
针对上述问题,本文通过引入Spearman相关性分析及聚类分析对马尔可夫链模型进行改进,提出一种基于住户差异性的马尔可夫链在室状态预测模型(Resident-differentiated,Markov Chain Occupancy Prediction Model with Cluster analysis,RMCPMC). 该模型综合考虑了不同特征参数对住户在室行为的影响差异,对住户进行合理的分类,在此基础上进一步建立在室状态预测模型. 本研究采用英国2000年TUS数据库对模型结果进行验证,并与传统马尔可夫链模型进行了对比分析.
1 在室状态预测模型
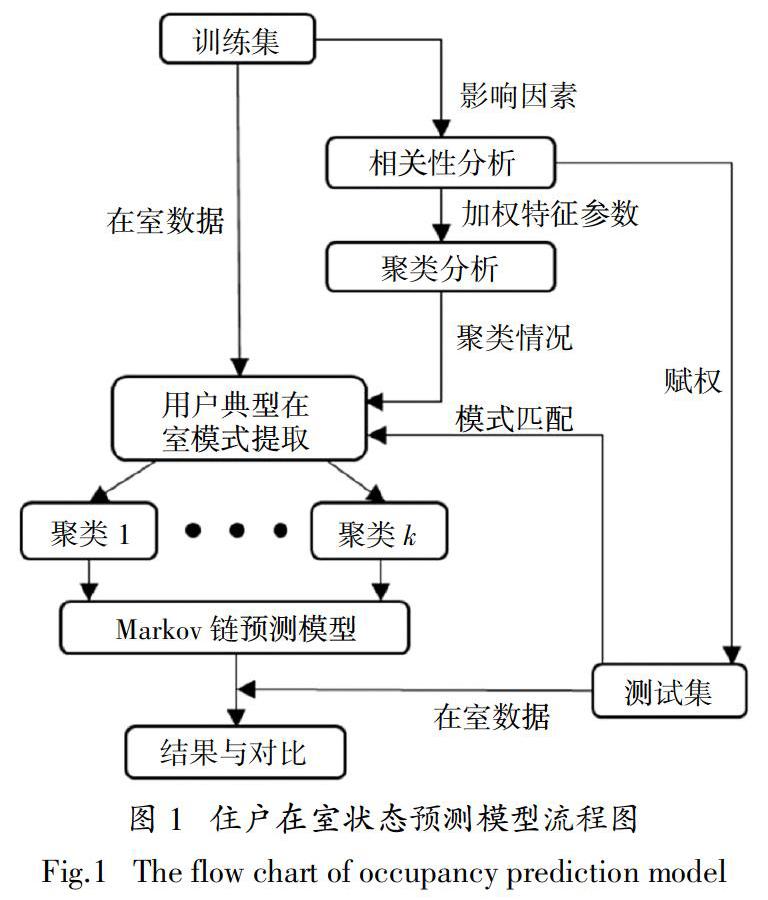
本文提出的基于相关性分析和聚类分析的住户在室状态预测模型流程如图1所示.
由图1可知,本研究所提出的模型主要包括以下步骤:
1)数据预处理. 对数据进行清理、筛选和转换,并通过随机抽样选取80%数据作为训练集,20%数据作为测试集[7].
2)特征参数选取及赋权. 通过Spearman相关性分析,计算不同特征参数与住户总在室时长之间的相关系数,在此基础上选取合适的特征参数,并将相关性系数作为权值赋予各特征参数.
3)典型住户在室状态模式提取. 将赋权后的特征参数作为对象特征,采用聚类分析将住户划分成若干类.
4)预测模型建立. 确定各类住户初始时刻在室状态概率和状态转移概率矩阵,以分别建立马尔可夫链预测模型.
5)模型验证. 对测试集住户进行在室模式匹配(即所属聚类类别),并采用各马尔可夫链模型分别进行预测,将预测结果与实际在室状态数据进行对比分析.
1.1 数据预处理
本文对原始数据的预处理过程主要包括数据清理、数据转换和无量纲化处理.
1)数据清理:由于不同因素影响(如调查对象漏填等问题),数据库存在部分住户数据不完整的情况. 为避免缺失数据影响模型结果,本文剔除该部分数据.
2)数据转换:数据库中所测参数的类型包括数值型(如住户年龄)和分类型(如住户性别). 不同类型的数据难以直接进行对比分析,因此本文将分类型参数转换为数值型参数,如住户性别为“男”则转化成数值1,反之则为2.
3)无量纲化处理:在应用过程中,取值范围小的参数易受取值范围大的参数影响而被忽略其重要性. 为此,本文对参数进行无量纲化处理,将不同参数的取值范围转化为相同区间,如[0,1][8].
1.2 Spearman相关性分析
由于住户不同特征因素对其在室行为的影响程度不同,有必要对其相关性进行分析,以确定不同影响因素对住户在室状态的影响程度. 本文采用Spearman相关性分析确定不同特征参数与住户总在室时长的关联程度. Spearman相关性分析是衡量2个变量的依赖性的统计方法,它利用单调方程评价2个统计变量的相关性. 其中相关系数用符号ρ表示,计算公式如(1)所示[9].
1.3 聚类分析
聚类分析是一种根据研究对象相似性将数据集划分为若干类或簇的过程,目的是保证“类内相似性和类间排他性”[10]. 本文选用划分聚类分析中k-means算法对加权特征参数进行聚类分析以得到不同住户群体,其核心思想为指定初始聚类类别及质心,并重复迭代直至算法收敛. 其最佳聚类数k可通过Calinski-Harabasz(CH)指标和Davies- Bouldin(DB)指标确定. 2指标包含对类内相似度与类间分离度的计算,CH指标越大而DB指标越小,则类内相似度和类间分散度越高,说明聚类效果更优. 本文采用开源数据挖掘软件RapidMiner[11]进行聚类分析,该软件是一个具有丰富数据挖掘分析和算法功能的开源软件,通过将不同功能的算子连接形成流程来实现其功能,简单易学且具有可视化特性.
1.4 马尔可夫链模型
该模型可通过初始在室概率p0和状态转移概率矩阵(Transition Probability Matrices,TPM)这两个参数进行描述. 将该模型应用于住户在室行为预测时,TPM的大小取决于在室状态数目(文中为“在室”和“离开”2种状态),如图2所示. 此外,考虑到在室状态具有动态变化特征,本文采用随模拟步长(即10 min)變化的不均匀TPM. 计算p0和TPM公式如下[14]:
在确定模型参数之后,为对在室状态进行随机预测,本文基于初始概率和状态转移概率矩阵,通过生成0-1之间的随机数并将其与相应累计概率分布比较推断出最可能出现的在室状态.
2 数据库与模型评价指标
2.1 数据库简介
英国国家统计局于2000年在全国范围内开展了时间利用调查,建立了Time Use Survey(TUS)数据库[15],该数据库以问卷调查的形式收录了约2万个住宅住户单人日志,且对所有月份及星期天数均有涵盖,其记录的详细日常活动信息能够提供丰富的住户行为数据. 这些日志主要包含两部分内容:
1)与住户日常活动相关的影响因素,包含详细的个人信息(如年龄、性别、民族、职业、收入、住户与其他住户的关系等)和住宅信息(住宅类型、家用电器及车辆拥有权、家庭收入等).
2)住户24 h(从4:00am到次日3:50am)具体的日常活动,包含一天工作日和一天非工作日,该信息是由住户主动记录每间隔10 min其主要日常活动、次要日常活动、相应位置及是否有陪同人员等.
2.2 模型评价
为评估模型的整体性能,本文采用平均绝对误差(Mean Absolute Error,MAE)和均方根误差(Root Mean Square Error,RMSE)两个指标对模型预测精度进行评价. MAE和RMSE反映预测在室状态概率的整体误差,计算公式如下:
3 结果与讨论
3.1 数据预处理结果
对TUS数据清理后共有12 166个住户日志数据完整且满足研究需求,本文选取这部分数据作为研究样本,并从样本中包含的日常活动分类中推断出在室情况,其具体信息见表1. 此外,从数据库中选取了12类可能对住户在室行为产生影响的因素,具体分类及内容见表2,其中表2中的分类数值均根据其相应顺序转为有序数值,例如,工作状态共计4种,依次编码为1~4.
3.2 相关性分析
本文以住户总在室时长为目标函数,对影响因素进行相关性分析,结果见表3. 由表3可知,在12个影响因素中,工作状态、身份信息、经济活跃情况和年龄与住户的总在室时长正相关系数较大,这意味着住户的这四类因素与住户在室持续时长具有显著相关性. 在分析和预测住宅建筑住户在室模式时,应重点考察这四种影响因素. 此外,住户住宅类型以及生活状况与总在室时长的相关性几乎为零,这表明二者对在室行为的影响可忽略不计. 因此在后续研究中将这两个因素剔除,最终选取10个影响因素作为聚类特征参数,并根据相关性系数为各特征参数赋予相应权值.
3.3 住户典型在室模式
在得到相关系数后,应以赋权特征参数为分类指标对训练集数据进行聚类分析. 针对不同聚类类别数目(本文设定范围为2~10),分别计算CH和DB指标,结果见表4. 由表4可知,在k=2时,CH指标最大,DB指标最小,即在保证类内相似最高的情况下类与类之间的距离最远,聚类效果最优. 因此,本文将样本住户分为2类进行研究.
表5为对赋权特征参数进行聚类后,2个聚类的聚类中心(即每个特征参数的平均值)、住户数量及占比情况. 图3给出了4个重要特征参数在这2个聚类的详细分布情况. 结合表5和图3可看出,第1类住户的工作状态、身份信息、经济活跃和年龄均为最大,这表明该聚类多为不在工作且不在学校、退休、经济状态不活跃、年龄较大的人员;第2类住户多为处于工作状态、拥有全职工作、经济状态活跃、年龄较小的人员.
由上述结果可看出两类住户具有明显不同的特征,为进一步分析不同住户特征对在室行为模式的影响,图4给出了两类住户的在室状态概率分布图. 从图中可知,两类住户的在室模式存在显著差异. 例如,在8:00—18:00时间段,第2类住户不在室概率明显高于第1类住户,其主要原因是第2类住户大部分为年龄相对较小的全职工作人员,白天通常处于外出工作状态;相反,对于第1类住户(年龄较大的退休或无工作住户),其主要日常活动为个人护理、休闲娱乐等室内活动,外出活动时间较短. 由此可知,两种在室模式与聚类所获取的住户特征较为吻合,表明基于住户典型特征参数能够合理划分住户并识别不同住户的在室行为模式,使得同一类住户的在室行为模式更为接近.
3.4 模型预测精度比较
在聚类分析所划分的两类住户的基础上,本文采用训练集建立了基于住户差异性的马尔可夫链在室状态预测模型(RMCPMC模型). 为验证模型的有效性,以测试集样本住户加权特征参数与两聚类中心的欧氏距离为依据评判住户归属典型类别,分别根据所建立的RMCPMC模型进行预测. 经分析测试集中有955名住户(39.25%)属于第1类,1 478名住户(60.75%)属于第2类. 为保证验证结果的公平性与合理性,应以数据集样本数目为模拟次数进行预测[4]. 因此,本文以测试集中各个聚类的样本数量为模拟次数模拟住户在室行为.
图5(a)(b)分别给出了RMCPMC模型和传统MC模型预测在室概率曲线与实际在室概率曲线对比图及相应的累计误差对比图. 结合两图可知,尽管2个模型均能大致刻画实际在室模式,但RMCPMC模型的累积误差上升速率明显小于MC模型. 这意味着RMCPMC模型预测误差明显低于传统MC模型. 其主要原因是传统的MC模型将所有住户视为同一群体进行预测分析,忽略了住户差异对在室模式的影响,导致基于训练样本计算的住户在室状态转移概率受个体差异的影响,与验证样本中的实际转移概率偏离较大. 而RMCPMC模型由于通过住户之间的相似性分别计算模型的转移概率,考虑了不同住户的特征差异,使得其预测结果更符合同类住户的实际在室情况. 值得强调的是,图5给出的在室概率与累计误差均为1 d的模拟结果,当将RMCPMC和MC 模型应用于在室行为长期预测时(如预测时长为1年,此时需将第一天的模型输出作为第二天的模型输入并不断推进),由于累积效应,RMCPMC模型预测在室概率误差和累计误差较传统MC模型会有更明显的降低,从而提高相应住宅建筑能耗预测精度.
表6给出了本文所提出的RMCPMC模型与传统MC模型的整体预测结果. 从表6中可知,相比于传统MC模型,本文所提出的预测模型的MAE和RMSE分别减少了20.57%和15.35%. 从总体预测结果来看,模型整体预测性能大幅提升. 这一结果表明,通过合理识别相似的建筑在室行为模式,能够实现提升在室行为预测精度的目的.
4 结 论
本文主要结论如下:
1)住户特征差异与建筑在室行为具有较强关联,因此在研究住户在室行为时应对住户不同特征与在室行为进行相关性分析. 就本文所采用的数据库而言,其中相关性较强的影响因素包括住户的工作状态、经济水平、年龄和身份信息.
2)本文方法能综合考虑住户差异性对建筑在室行为的影响,通过合理区分不同建筑住户特征以识别相应的典型在室模式. 本次研究通过聚类分析获得2类具有明显不同特征的住戶:第1类住户多为不在工作且不在学校、退休、经济状态不活跃、年龄较大的人员;第2类住户多为处于工作状态、拥有全职工作、经济状态活跃、年龄较小的人员. 且两类住户在室模式与聚类所获取住户特征较吻合.
3)与传统MC模型相比,RMCPMC模型整体预测精度显著提升,RMCPMC模型可根据住户特征参数有效判别住户所属类别,获得更加合理的模型输入参数,预测结果更符合实际,模型预测误差MAE和RMSE分别减少了20.57%和15.35%.
本文模型的建立和评估均是以英国2000年TUS数据库为例,将其应用于我国时应结合我国住宅建筑室内人员特征,从数据采集、模型参数选取和聚类分析参数权重分配等方面进行考虑. 同时,就新建住宅住户行为预测而言,考虑到其住户特征难以获取,应基于其规划设计信息选择已有类似住宅并采用相关参数进行预测,在后期业主入住后再收集住户信息对模型进行校核和修正.
此外,本文研究主要针对建筑住户在室状态(即在室和不在室)的预测进行分析和验证,在此基础上,未来应进一步细化住户在室行为(如主动/被动在室状态、与能耗相关行为等)建立相应预测模型,以获取住户更全面且详细的在室状态,并将其与能耗预测模型相耦合,达到提高能耗模拟精度的目的.
参考文献
[1] LABEODAN T,ZEILER W,BOXEM G,et al. Occupancy measurement in commercial office buildings for demand-driven control applications-A survey and detection system evalua-tion[J]. Energy and Buildings,2015,93:303—314.
[2] 俞准,周亚苹,李郡,等. 建筑用户在室行为预测新方法[J]. 湖南大学学报(自然科学版),2019,46(7):129—134.
YU Z,ZHOU Y P,LI J,et al. A new approach for building occupancy prediction[J]. Journal of Hunan University (Natural Sciences),2019,46(7):129—134. (In Chinese)
[3] JIA M D,SRINIVASAN R S,RAHEEM A A. From occupancy to occupant behavior:an analytical survey of data acquisition technologies,modeling methodologies and simulation coupling mechanisms for building energy efficiency[J]. Renewable and Sustainable Energy Reviews,2017,68:525—540.
[4] RICHARDSON I,THOMSON M,INFIELD D. A high-resolution domestic building occupancy model for energy demand simulations[J]. Energy and Buildings,2008,40(8):1560—1566.
[5] FLETT G,KELLY N. An occupant-differentiated,higher-order Markov Chain method for prediction of domestic occupancy[J]. Energy and Buildings,2016,125:219—230.
[6] AERTS D,MINNEN J,GLORIEUX I,et al. A method for the identification and modelling of realistic domestic occupancy sequences for building energy demand simulations and peer compar-ison[J]. Building and Environment,2014,75:67—78.
[7] 周志華.机器学习[M]. 北京:清华大学出版社,2016:25.
ZHOU Z H. Machine learning[M]. Beijing:Tsinghua University Press,2016:25. (In Chinese)
[8] 李郡,俞准,刘政轩,等. 住宅建筑能耗基准确定及用能评价新方法[J]. 土木建筑与环境工程,2016,38(2):75—83.
LI J,YU Z,LIU Z X,et al. A method for residential building energy benchmarking and energy use evaluation[J]. Journal of Civil,Architectural & Environmental Engineering,2016,38(2):75—83. (In Chinese)
[9] 陈功平,王红. 改进Pearson相关系数的个性化推荐算法[J]. 山东农业大学学报(自然科学版),2016,47(6):940—944.
CHEN G P,WANG H. A personalized recommendation algorithm on improving Pearson correlation coefficient[J]. Journal of Shandong Agricultural University (Natural Science Edition),2016,47(6):940—944. (In Chinese)
[10] HAN J W,KAMBER M,PEI J. Data mining:concepts and techniques [M]. 3rd ed. Beijing:China Machine Press,2012:448—450.
[11] NAIK A,SAMANT L. Correlation review of classification algorithm using data mining tool:WEKA,rapidminer,Tanagra,orange and knime[J]. Procedia Computer Science,2016,85:662—668.
[12] FOUTZ R V,GRIMMETT G R,STIRZAKER D R. Probability and random processes[J]. Journal of the American Statistical Association,1993,88(424):1475.
[13] 李欣然,陳鸿琳,冷华,等. 中长期电量预测的傅里叶-马尔科夫修正模型[J]. 湖南大学学报(自然科学版),2016,43(10):62—69.
LI X R,CHEN H L,LENG H,et al. Mid-long term load forecasting model with Fourier series and Markov theory residual error correction[J]. Journal of Hunan University (Natural Sciences),2016,43(10):62—69. (In Chinese)
[14] WID?魪N J,W?魨CKELG?RD E. A high-resolution stochastic model of domestic activity patterns and electricity demand[J]. Applied Energy,2010,87(6):1880—1892.
[15] Ipsos-RSL and Office for National Statistics. United Kingdom Time Use Survey,2000. [EB/OL]. [2003-09]. https://census.ukdataservice.ac.uk/.

