趣味数学——牛吃草问题

不少同学认为数学是难度较大的学科，其实提高编程水平可以帮你理解很多奥数难题。今天这道牛吃草问题据说最初是由牛顿提出的。

牧场上有一片青草，每天增长相同数量，这片青草供给10头牛吃可以吃22天，16头牛吃可以吃10天。如果供给25头牛吃，可以吃多少天？

通过四步可以解这道题：1.求出每天增长草量。2.求出牧场原有草量。3.求出每天实际消耗原有草量（牛吃的草量-增长的草量=消耗原有的草量）。4.求出25头牛吃多少天。

下面先用传统数学解题思路：

1. 设每头牛每天吃1份草，10×22=220（份）（原有草量+22天每天增长草量），16×10=160（份）（原有草量+10天每天增长草量）。

2. 220-160=60（份） 22-10=12（天）（12天增长的草量等于60份），60÷12=5（份）平均每天增长的草量为5份。

3. 25头牛每天消耗原有草量：25-5=20（份）25头牛每天吃的分量-每天增长的草量。

4. 原有的草量：22×10-22×5=110（份）或16×10-10×5=110（份），10頭牛吃22天的分量减去22天增长的草量。

5. 25头牛能吃：110÷20=5.5（天）

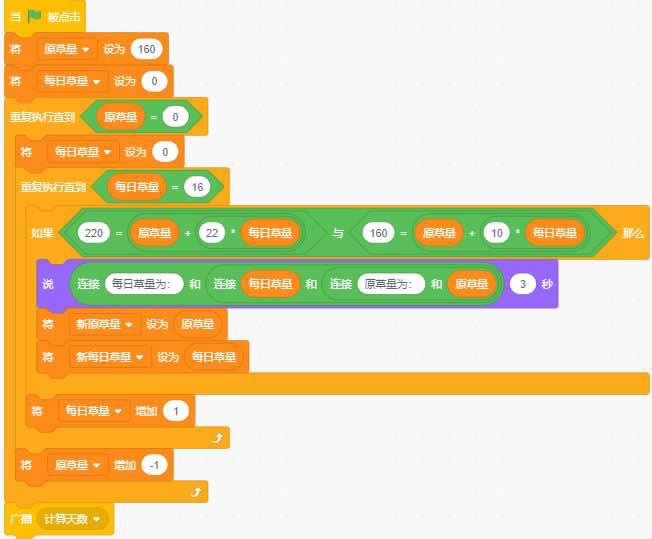
此外还可以用解方程的方法：设牧场原有草量为y，每天新增加的牧草可供x头牛食用，25头牛能够在n天将草全部吃完，根据题目条件可以得出三个方程式：

22×10=y+22x、16×10=y+10x 和25n=nx+y解方程得到： y=110 x=5 n=5.5

用方程解决牛吃草问题的核心公式是：原有草量=（牛数-单位时间长草量可供应的牛的数量）×天数。我们将方程思想带入到Scratch中就可以解决牛吃草的问题了。

初始情况下设置原草量为160，每日增长的草量为0，利用和鸡兔同笼相同的循环方法先求出22×10=y+22x 和 16×10=y+10x两个方程组的解x=5 y=110。然后将原草量和每日草量的值代入到计算天数的环节中，利用循环来计算出天数，由于天数的变化可能存在半天的情况，所以我们这里将天数每次增加设置为0.5。计算得出最终的答案为：每日增长草量为5，原草量为110，25头牛可以吃5.5天。

通过解方程思路结合编程思想解决牛吃草的问题，总结该类问题的通用公式：

1. 每天增长草量= （吃得较多天数×对应牛头数-吃得较少天数×对应牛头数）÷（吃得较多的天数-吃得较少的天数）

2. 原有草量=牛头数×吃的天数-每天增长草量×吃的天数

3.吃的天数=原有草量÷（牛头数-每天增长草量）

4. 牛头数=原有草量+吃的天数+每天增长草量