基于有限元方法的柔性立管防弯器疲劳寿命分析

刘军鹏，齐华林，罗晓兰，张振兴，张 涛

(1. 中国石油大学(北京) 安全与海洋工程学院，北京 102249; 2. 中国石油大学(北京) 机械与储运工程学院，北京 102249; 3. 海洋石油工程股份有限公司，天津 300450)

柔性立管在深水油气田开发中已被广泛应用，其与浮式生产系统的连接部位是动态分析和疲劳寿命分析的关键区域，主要是因为浮体运动引起大的拉伸变形和动态弯曲载荷的长期作用。防弯器(bend stiffener)用于柔性立管和浮体连接处的平稳过渡，是柔性立管系统的关键附件，如图1(a)所示，其主要作用是降低此区域柔性立管过度弯曲变形的风险和提高立管的疲劳寿命。工程应用的防弯器几何形态主要有一段到三段结构形式，其中基本构型为圆锥状的三段式结构最为典型，如图1(b)所示。由于防弯器处于工况最为恶劣区域且需长期动态应用，疲劳破坏是其最容易发生的失效模式，因此对防弯器进行疲劳寿命分析既是保证柔性立管系统在位安全的需要，也是油田和设备未来延寿评估的基础，具有十分重要的工程意义。针对柔性立管防弯器的研究面临诸多难点和挑战，主要来源于多种非线性因素的影响：防弯器的材料为聚氨酯弹性体，其本构关系为非线性；柔性立管防弯器长期受复杂多变的动载荷作用，其结构整体会产生大的变形，几何方程需要用非线性形式来表征；柔性立管从防弯器内部贯穿而过，在风、浪、流的作用下柔性立管会随机运动，进而带动防弯器运动，期间，防弯器的内壁与柔性立管的外壁之间的间隙、接触面和力的大小及分布都是动态变化的，属于接触非线性问题。

图1 防弯器Fig. 1 Bend stiffener

从20世纪60年代至今对防弯器力学性能及疲劳寿命的研究从未间断。Deruntz[1]首次提出应用细长梁理论，来分析防弯器和线弹性立管的组合问题。Boef 和 Out[2]在Deruntz研究基础上，考虑了大变形条件，并首次应用到防弯器的设计上。Lane等[3]开发了首款用于防弯器初步设计的软件STIFFENER。规范API 17B2002[4]中提到，根据Pesce提出的理论方法，在柔性立管防弯器区域，靠近防弯器自由端的柔性立管加载外力—角度载荷，采用有限元法对防弯器整体结构进行分析计算，获得防弯器整体变形和应力分布情况。Vaz 等[5]首次提出了防弯器的几何和材料非线性力学模型，并从线性和非线性两种情况进行了对比分析，结果表明在实际工程设计中应重视防弯器非线性问题。Vaz等[6]考虑了防弯器的几何兼容性，力和力矩的平衡以及非线性不对称材料本构关系，得到一组四个一阶非线性常微分方程及在两端指定四个边界条件。Caire[7]基于黏弹性理论描述聚氨酯行为，提出了用数学模型来表示柔性立管防弯器系统。Dong等[8]提出了防弯器尖端角度设计所需的精确表达式。Caire 等[9]考虑了几何和材料非线性，以及大变形条件，建立了防弯器非线性黏弹性时域方程，并通过案例研究了不同加载频率下防弯器的系统响应。Caire等[10]采用扰动方法对非线性黏弹性防弯器大挠度梁模型进行谐波加载条件，得到了稳态公式(忽略惯性力)和数值求解程序。席勇辉等[11]基于异型梁单元和等效弯曲刚度，提出了用于防弯器数值分析的计算方法，结合案例评估了此方法的适用性。谢宗伯[12]提出了基于失效模式防弯器的设计方法。Smith[13]提出了在极限载荷条件下防弯器的设计过程，以及提高防弯器疲劳寿命的方法。Demanze等[14]基于有效应变强度因子理论，并提出了疲劳门槛值的概念，分析了关键区域防弯器疲劳寿命评价方法，与有限元分析对比，提出了应变计算原理的校准，最后根据全尺度和中尺度测试结果对方法进行全面校准(Technip公司开发的创新方法)。Doynov等[15]针对墨西哥湾深水工程期间进行的全面疲劳验证测试中防弯器的失效原因进行了详细分析，具体表现为内部和外部裂纹在防弯器不同位置延伸。Dos Santos[16]提出了一种新的防弯器失效判据，采用聚合物滑动磨损率作为粗糙度函数，可以可靠地预测表面疲劳失效，但该模型证明仅对高周疲劳失效有效，其中含裂纹萌生期对疲劳寿命影响最大。

可以看出，柔性立管防弯器区域一直是局部分析的热点，常规的分析方法是将防弯器看作为柔性立管顶端的附件，二者互为一体，建模时把防弯器和柔性立管的顶端都固支，且忽略他们之间的间隙和摩擦，如图2(a)所示，很明显该方法结果比较保守。以南海某油田防弯器为例，建立如图2(b)所示的“管中管”有限元分析模型，考虑了防弯器和柔性立管之间的间隙和滑动摩擦，能够真实地反映两者之间的相互作用，此外，在加载方式上，利用“端部位移”载荷取代传统的“力—角度”载荷方式，更加符合工程实际。基于有限元分析和防弯器疲劳试验结果，计算疲劳寿命。提出基于有限元模型的柔性立管防弯器疲劳寿命方法，既可为防弯器的优化设计提供借鉴，也可为油田延寿提供参考。

图2 柔性立管—防弯器配合模型Fig. 2 Interaction model for flexible riser and bend

1 柔性立管防弯器有限元模型

1.1 模型建立

以南海某油田的防弯器和柔性立管为例，考虑了防弯器和柔性立管之间的间隙和可能出现的滑动摩擦，以及几何非线性和接触非线性，采用ABAQUS建立柔性立管防弯器的管中管三维有限元模型。防弯器构型如图3所示，几何参数见表1。与该防弯器相配合作业9.25英寸的柔性立管其内径为234.9 mm，外径为317.93 mm，几何模型长度设置为11 299 mm。

图3 南海某油田防弯器构型Fig. 3 Configuration of the bend stiffener in some field of the South China Sea

表1 南海某油田防弯器尺寸参数Tab. 1 Dimensional parameters of the bend stiffener in some field of the South China Sea

应用六面体单元划分网格，考虑到防弯器自由端容易形成应力集中问题，对其几何结构进行分割，在不同位置布置不同密度的种子，尤其在自由端加密种子布置，提高精度和收敛性。立管和防弯器均会承受弯曲载荷的作用，也存在大变形、接触、挤压和摩擦问题，因此，均选择8节点六面体线性减缩单元，采用面面接触，力学约束方程采用运动学的接触算法，滑动方程选择有限滑动，设置滑动摩擦系数为0.5[17]。

如果结构的变形使体系的受力发生了显著的变化，以至不能采用线性体系的分析方法时就称为几何非线性，即力—位移关系不再是直线，如结构的大变形、大挠度问题等。含防弯器的柔性管弯曲就是这种大变形问题。分析中，打开ABAQUS中几何非线性开关，即Nlgeom的状态为ON，确保每一个设置与实际工况条件一致，以保证最终的计算精度，网格划分情况如图4所示。

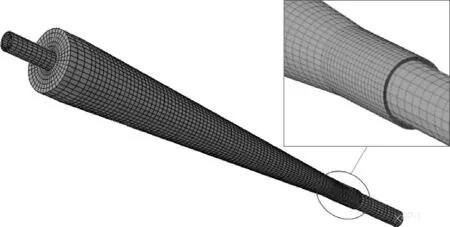
图4 柔性立管防弯器网格划分情况Fig. 4 Grid division of flexible riser and bend

材料属性设置时，考虑到柔性立管只作为防弯器有限元分析的一个边界条件，柔性立管材料为金属和非金属组成的多层复合结构物，其每一层的材料属性都不尽相同，因此，把多层柔性立管等效成一层，不必精细化建模，基于该柔性立管的弯曲刚度试验参数，根据圆管的弯曲刚度公式[18]计算其弹性模量，如图5所示。

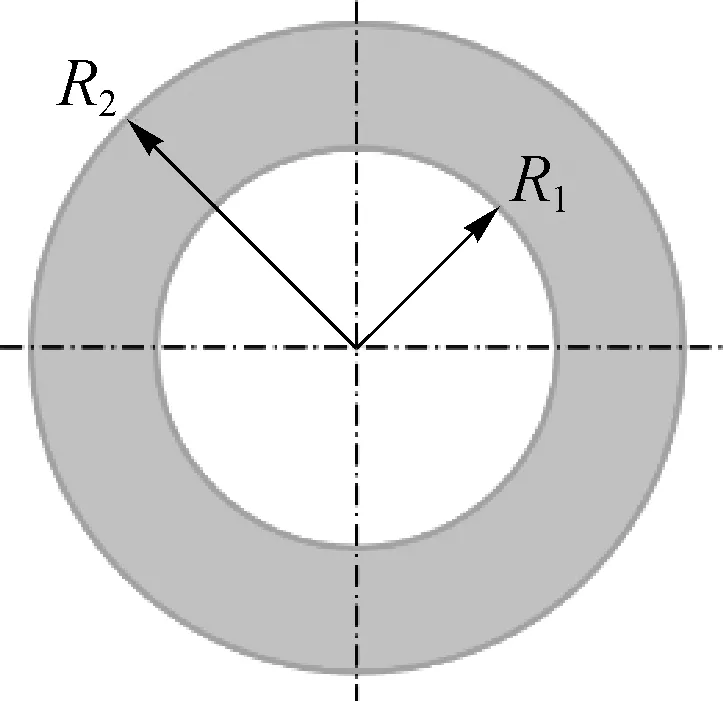
图5 等效柔性立管Fig. 5 Equivalent flexible riser

(1)

其中，EIpipe为柔性立管弯曲刚度，其值为35.519 kN·m2；E为柔性立管等效弹性模量；R2为柔性立管的外径；R1为柔性立管内径。把相关数据代入式(1)中，计算得到等效弯曲弹性模量约为100.936 MPa；根据该柔性立管的试验参数，其密度的最大值为9.9×10-10t/mm3。考虑到聚氨酯为超弹性材料，其具有非线性本构关系，采用谢宗伯[12]的试验数据(如图6)作为其材料属性，将应力—应变曲线直接输入到ABAQUS，然后进行材料评估即可得到其材料本构参数；防弯器密度设置为9.776×10-10t/mm3。

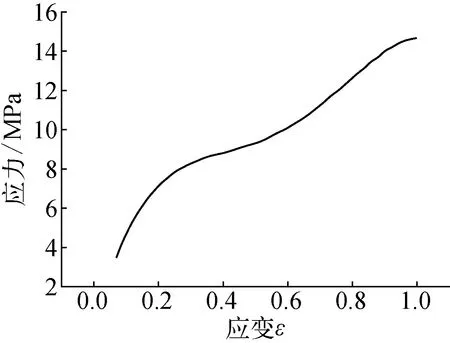
图6 聚氨酯弹性体应力—应变曲线Fig. 6 Stress-strain curve of polyurethane elastomer

针对柔性立管防弯器有限元模型的加载，常规方法是在柔性立管末端部加载“外力—角度载荷”，主要认为拉力对立管的曲率影响最大，但该载荷很难反映实际工程中的数值，也较难测得。考虑到运动响应是拉力和动态载荷联合作用下的综合表现形式，而且运动响应在实际工程中也相对容易通过监测手段获得，因此，提出在柔性立管末端部加载三向位移，把运动监测数据和柔性立管防弯器的有限元分析有机结合，更加符合工程实际，两种加载方式见图7。

图7 柔性立管弯管器两种加载方式Fig. 7 Two loading methods of flexible riser bend stiffener

为了简明地说明问题，以幅值为A的工况的正弦信号来表征动态变化位移载荷：

(2)

(3)

1.2 分析结果

分别计算了x、y方向上的幅值A为500、1 000、1 500、2 000、2 500五种载荷情况下，防弯器的结构响应。很明显，在1/4周期时，防弯器具有最大应力。取x和y方向上最大位移幅值为1 000的工况在第1/4周期时的应力分布和变形云图如图8、图9所示；变形最大位置处于防弯器自由端的边缘区域，具体位于节点ASSEMBLY.1，此外，从变形云图可以发现，防弯器从顶端到自由端，变形情况逐渐明显。

图8 防弯器应力和位移云图Fig. 8 Stress and deformation contour of bend stiffener

图9 沿防弯器危险截面建立的周向和轴向路径Fig. 9 Circumferential and axial paths established along the dangerous section of bend stiffener

在载荷一定的条件下，应力最大之处就是危险截面，疲劳破坏从该处最先发生。从应力最大处沿周向建立路径如图9所示。 建立最大应力结点所处位置的自下而上的轴向路径。不同幅值载荷，轴向路径的各结点应力分布可以表征最大应力以及危险截面所在的在轴向方向上的位置；不同危险截面周向路径应力分布表明了不同的位移幅值会影响防弯器危险截面的应力大小以及对疲劳的敏感程度。同时可以发现，随着载荷的增加，危险截面的位置会向上移动。根据所施加的5种载荷情况的仿真结果统计周向和轴向路径的应力如图10、图11所示，可以发现位于防弯器弯曲形状外侧和内侧的应力较大，当位移幅值较大时的应力最大位置主要出现在防弯器偏上部的位置。

图10 防弯器危险截面周向应力分布Fig. 10 Circumferential stress distribution of dangerous section of bend stiffener

图11 防弯器最大应力处轴向方向应力分布Fig. 11 Stress distribution in the axial direction at the maximum stress of the bend stiffener

2 防弯器疲劳寿命计算

2.1 疲劳寿命分析方法

研究防弯器疲劳寿命最可靠的方法是在实际工况条件下对其进行全尺寸疲劳试验，但这需要高昂的试验费用和较长的时间。目前主要通过在实验室内对防弯器的材料进行疲劳研究，然后对材料测试数据进行拟合得到疲劳寿命曲线。

针对防弯器所用的聚氨酯弹性体材料，其疲劳损害机理比较复杂，目前用于研究非金属类材料疲劳寿命的方法主要包括应力疲劳分析法和应变疲劳分析法，实际工程上对于应变的测量相对容易，且关于防弯器疲劳都基于应变疲劳分析，可借鉴的有效资料多，因此选用应变疲劳分析法，即ε-N曲线法。

De Marco Meniconi等[19]选取防弯器顶端连接段的样品进行了疲劳测试，试样厚度为30 mm，加持孔径为24 mm，采用伺服试验机加载循环牵引载荷，加载频率为3 Hz，试验为避免热疲劳带来的影响，利用热电偶来监测材料的温度。具体试样及试验如图12所示，疲劳试验结果如图13所示。

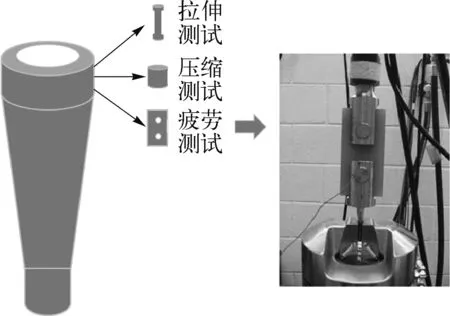
图12 防弯器材料疲劳测试[19]Fig. 12 The fatigue test of bend stiffener[19]

图13 防弯器应变—循环次数曲线[19]Fig. 13 The strain-number of cycles curve of bend stiffener[19]

将其横纵坐标转化为均匀坐标后，可以拟合得到应变—循环次数公式：

N=2×107e-63.12ε

(4)

其中，N为循环次数；ε为应变范围。

2.2 疲劳寿命计算结果

聚氨酯防弯器工况复杂，等效应力参数可用于评估聚氨酯防弯器在复杂载荷工况下的疲劳寿命。根据1.1节的有限元分析模型，可以获得防弯器危险截面的Mises应力结果。因为有限元中的Mises应力是等效应力结果，可以清楚地描述结果在整个模型中的分布和快速确定模型中最危险的区域。

采用谢宗伯[12]根据聚氨酯弹性体材料拉伸试验得到的应力—应变曲线来分析防弯器应变情况，将试验数据点用四次多项式拟合，具体见图6所示，可得到如下函数关系式：

σf=-89.947ε4+214.95ε3-173.15ε2+62.912ε-0.089 6

(5)

其中，σf表示等效应力；ε表示等效应变。将1.2节中有限元计算的Mises应力值代入式(5)，根据实际情况，取方程的正实根，从而获得相应的等效应变值。根据式(4)防弯器材料的疲劳寿命表达式，进一步推导出循环次数的数学表达式，并把N作为防弯器的疲劳寿命。

由计算公式可知，防弯器的最大应力或者最大应变区域即为其最先达到疲劳寿命的地方，因此这里只计算各幅值工况下最大应力位置的疲劳寿命，计算结果如表2所示。由表2可知，随着载荷幅值的增大，防弯器的应力和应变也逐步增大，并且其所允许的循环次数急剧下降。

表2 防弯器各工况危险截面疲劳寿命的计算Tab. 2 Calculation of the fatigue life of the dangerous section of the bend stiffener under various working conditions

3 结 语

以中国南海某柔性立管防弯器为例，对其进行有限元分析，关注聚氨酯材料的非线性对防弯器性能的影响，以及载荷大小对防弯器危险截面区域的影响。基于有限元模型分析结果，计算出防弯器危险截面的疲劳寿命。在有限元建模时选用的“管中管”模型，相比传统的附件模型，能够更好模拟防弯器和柔性立管之间的间隙和可能出现的滑动摩擦，此外，在加载方式上提出用“位移”载荷取代传统的“力—角度”载荷，此建模方法和加载方式更符合工程实际，特别是随着监测技术的进步，对立管的运动监测结果更加准确，利用此监测结果作为有限元模型的载荷输入，亦非难事。以模型结果为基础，结合防弯器材料的应力—应变曲线和ε-N疲劳试验曲线，可求得防弯器危险截面的疲劳寿命。提出的方法思路可为防弯器的优化设计提供参考，也可为油田及设备延寿评估提供借鉴。