一种基于模糊控制的岸边集装箱起重机防摇策略＊

秦仙蓉 王玉龙 郝婼兰 张 氢 孙远韬

同济大学机械与能源工程学院 上海 201804

0 引言

为提高岸边集装箱起重机（以下简称岸桥）的装卸效率，在实现小车位置的同时减小吊重的摇摆是需要解决的关键问题。目前，采用的防摇装置主要有机械式防摇装置与电子防摇装置。机械式防摇主要是通过增大悬挂刚度或安装阻尼器的方法来实现，最常见的有八绳防摇系统[1]、液压减摇系统等。而在实际应用中，机械防摇外围设备多、结构复杂引、起的机械磨损和能量损耗较大，且机械防摇方式虽然可以减小摆动，但无法快速将摆动消减到一个很小的范围内，可靠性较差。因此，在机械防摇的基础上增加电子防摇措施，成为目前常用的防摇方式。

钟斌等[2]将门式起重机吊重系统简化为小车-吊重系统，研究了吊重摇摆的规律和影响因素，考虑到小车-吊重系统某些状态变量不易直接测量，设计了状态观测器来估计状态变量信息，然后提出了基于极点配置的吊重防摇反馈控制方法，取得了较好的防摇效果。翟军勇等[3]以桥式起重机这类欠驱动系统为研究对象，分析了小车运行加速度和吊重摆角之间的关系，据此建立了集装箱桥式起重机小车系统的动力学模型，然后提出了一种防摇控制算法，将测得的吊重摆角信号反馈到防摇控制系统中，构建了闭环控制系统，通过计算机仿真和实际试验，验证了所提出的算法可以提高小车迅速消摆的能力。Adeli等[4]将桥式起重机小车-吊重系统简化成了一个平面双摆模型，根据Takagi-Sugeno模糊模型，将此非线性系统近似成多个线性子系统的集合，然后用线性二次调节（LQR）方法，得到了每个子系统的LQR调节器，然后用平行分布补偿法设计了平行分布模糊LQR控制器，实现了对起重机吊重系统的位置调节和防摇控制。

本文基于模糊控制的基本原理，选出控制量，制定模糊化规则，设计出模糊控制器，构造岸桥防摇混合控制系统，仿真实现对吊重摆角的控制，并与双比例微分（PD）控制系统进行了对比，证明控制算法的有效性和优越性。

1 简化力学模型的建立

建立岸桥前大梁-小车-吊重系统的简化力学模型，如图1所示。

图1 前大梁-小车-吊重系统简化力学模型

为分析耦合系统中，前大梁振动对吊重摆动的影响，在图1所示模型的基础上，假设前大梁是刚性的，可以对系统进一步简化，力学模型如图2所示。

图2 小车-吊重系统简化模型

为了比较两个模型下的吊重响应的区别，以相同的小车运动特性（图3）作为激励，分别求解两个系统的吊重摆角响应，结果如图4所示。

图3 小车加速度曲线

图4 两种模型吊重摆角响应

图4中两条曲线基本吻合，没有显著的区别，说明在图3所示的小车运行特性下，岸桥前大梁的振动对吊重摆角响应的影响很小，可以忽略不计。因此，在后续的控制过程中，忽略前大梁的影响，采用小车-吊重系统进行控制系统的设计与仿真。

2 防摇控制策略设计

小车吊重系统有两种控制方式可供选择[7]：一种是力控制方式，可以通过控制电机的输出力矩来控制吊重的摆动，另一种是速度或加速度控制方式，通过控制电机转速来控制小车速度或者加速度，从而减小吊重摆动。本次设计中，选用加速度控制。

为了使小车能够按照既定的轨迹运行，同时能够消除吊重的摆动，设计如图5所示的控制策略，使用位置跟踪控制器来跟踪小车既定轨迹，摆角控制器抑制小车运行过程中吊重的摆动。

图5 防摇控制策略示意图

3 混合控制系统设计

本节将模糊控制与PD控制组成混合控制系统来实现岸桥吊重摆角的控制。

模糊控制是建立在模糊数学基础上、能模拟人的决策过程的一种控制方法，是模糊系统理论在控制技术上的应用。二维模糊控制基本原理如图6所示，其中r为参考量，yout为表示系统的输出，e=r-yout为误差，为误差变化率，u为模糊控制器的输出量，ke、ke和ku为模糊控制器输入输出值的模糊量化因子。

图6 模糊控制原理框图

将模糊控制方法与传统的PID控制算法相结合，设计了混合控制系统，其控制框图如图7所示，其中PD控制器用于跟踪小车的位置，模糊控制器用于抑制小车运行过程中吊重的摆动。

图7 混合控制系统框图

模糊控制器的输入为吊重偏摆的角度θ和角度变化率，位置跟踪控制器的输入为小车的位移x和速度，两个控制器的输出量均用于调节小车电机的加速度，从而实现小车位置的跟踪和吊重摆角的控制。

4 模糊控制器设计

确定模糊控制器的输入变量为：吊重的摆角θ和摆角变化率；模糊控制器的输出变量为小车加速度控制分量u。

1）模糊化

根据图3小车运行参数以及图4所得的摆角响应，确定输入输出变量的论域分别为摆角θ∈[-0.08，0.08]rad，摆角变化率∈[-0.08，0.08] rad/s，小车加速度控制分量u=∈[-0.5，0.5] m/s2。

为了便于工程实现，一般将输入范围人为定义成离散的若干等级，定义级数的多少取决于所需输入量的分辨率，一般情况下定义级数为3～9级，等级定义越多，控制分辨率越高，但控制规则数增加；若减小等级数，模糊控制规则数减少，但控制分辨率降低，故等级数目一般取6或7[5]。此处，取等级数目为7（如图8的NB～PB，其分别表示负大、负中、负小、零、正小、正中和正大）。

模糊语言值实际上是一个模糊子集，最终需要通过隶属度函数来进行描述。隶属度函数的定义方法很多，最简单的是三角形公式表示法，此方法虽简单，但完全满足隶属度函数的所有需求，并且实际操作中有很多方便，故本文采用此方法定义三个变量的隶属度函数μθ、μout(μ)和μu。以μθ为例，其图像如图8所示，其余两个可以按论域类推。

图8 输入变量θ的隶属度函数

2）模糊推理

制定本模糊控制器的模糊规则，首先，重述各输入输出量的正负号定义，如图9所示。

图9 输入输出符号定义

根据实际的控制经验，可以得到结论：当摆角θ＞0时，若小车加速，则摆角减小；当摆角θ＜0时，若小车减速，则摆角减小；当摆角θ＝0时，摆动角速度为正大时，若小车加速，则摆角减小；当摆角θ＝0，θ＝0摆动角速度为负大时，若小车减速，则摆角减小。

根据上述实际经验，制定模糊控制规则如表1所示，共49条规则。设定好模糊控制规则后，需要根据输入量和模糊控制规则，进行模糊推理，以得到输出量的隶属度值。这里采用最大最小法进行模糊推理[6]。例如输入某和时，规则R1和R2被激活，则

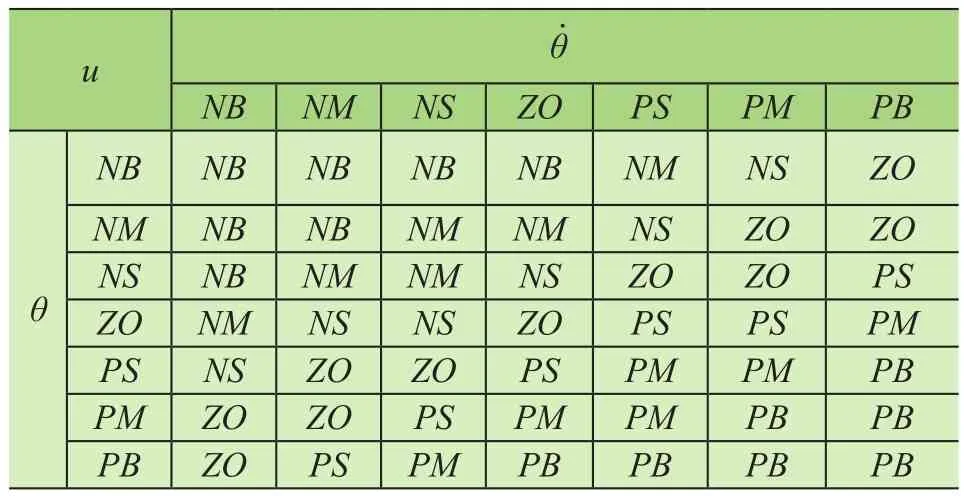
表1 模糊控制规则表

3）去模糊化

通过模糊推理得到的结果μout(u)是一个模糊量，但实际模糊控制系统所需要的控制信号必须是精确量。因此模糊推理后的模糊输出量必须经过去模糊化处理，才能去控制被控对象。常用的去模糊化方法有最大隶属度法、面积重心法和加权平均法等。

面积重心法不仅有公式可循，而且也有较为合理的理论解释，而且运用了模糊集合的所有信息。此外，它还根据隶属度的不同而调整侧重点，故本文选择面积重心法[7]进行去模糊化处理。

5 系统仿真

采用Matlab—Simulink中的Fuzzy Logic Controller模块定义模糊控制器，通过调节参数，最终得到混合控制系统仿真结果如图10和图11所示。

图10 系统仿真时小车加速度曲线

图11 系统仿真吊重摆角曲线

在图11中，tr=25.5 s为原加速工况时，小车停止运行的时刻；ts=33 s为混合控制系统控制时，小车停止运行的时刻。由此可知，运用控制器控制后，小车总运行时间延长了7.5 s。

在添加控制系统后，小车运行时，吊重摆角从0.089 rad减小到了0.050 rad；小车停止运行时，吊重由小幅度摆动变化为无摆动，可直接进行下降操作。可以看出，混合控制器控制吊重摆动的效果良好。

6 系统仿真对比

为了验证所设计的混合控制器的有效性，设计如图12所示的双PD控制系统用于防摇，图13为双PD控制系统与混合控制系统的仿真结果对比。

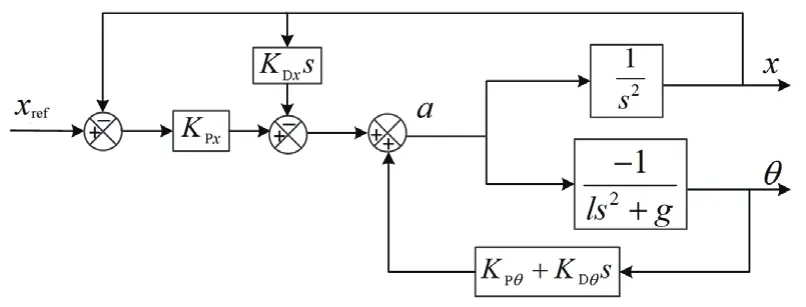
图12 双PD控制系统框图

图13 双PD与混合控制系统仿真结果对比

由图13所示控制结果可以看出，两种控制系统的吊重摆角控制效果近似，但混合控制系统控制下，当ts=33 s时，吊重已经停止摆动，双PD控制器控制下；当tp=36 s时，吊重停止摆动。因此，所设计的混合控制系统能够较快地稳定，这也证明了模糊控制算法的优越性。

7 结论

基于模糊控制的原理，采用小车加速度控制方式和位置跟踪，建立了模糊控制和PD混合控制系统，通过Simulink进行系统仿真，结果显示混合控制系统可以很好地控制吊重的摆动，达到防摇的目的，证明了模糊控制的有效性及可行性。

同样建立小车加速度控制的双PD控制系统，与混合控制系统进行仿真结果对比，发现两种控制系统防摇控制效果基本相同，但混合控制系统比双PD控制系统较快达到稳定。说明模糊控制的延时较低，速度较快，比双PD控制更有优越性。