一种多样性控制的多目标粒子群算法
刘天宇,王 翥
(1.上海海事大学 信息工程学院,上海 201306;2.上海海事大学 物流工程学院,上海 201306)
现实生活中的很多问题都可以抽象化为具有多个相互冲突目标的多目标优化问题。近些年来,采用进化算法来处理多目标优化问题已经成为研究热点之一。其中,粒子群算法作为一种经典的群智能算法,由于其参数少及容易实现的特点,被广泛地应用于求解各种多目标优化问题[1-3]。
对于包括多目标粒子群算法(Multi-Objective Particle Swarm Optimization,MOPSO)[4]在内的多目标进化算法,算法设计的关键在于达到种群多样性及收敛性之间的平衡,以便有效产生一组同时优化多个冲突目标的Pareto最优解集。针对上述问题,目前已经出现了许多改进的MOPSO算法。一些改进算法通过将MOPSO与各种多样性保持策略及局部搜索策略相结合,来更好地平衡算法的收敛性与多样性。YU等[5]通过将多种群策略与多目标粒子群算法相结合,提出了一种基于多种群动态协同的多目标粒子群算法。HAN等[6]提出了一种自适应的多目标粒子群算法AGMOPSO。该算法通过采用自适应飞行参数来控制粒子在搜索空间的移动,进而平衡算法的收敛性和多样性。
此外,另一影响MOPSO算法性能的关键在于如何对种群中的每一个粒子获取合适的全局及个体最优位置,以提高算法的搜索有效性[7]。针对这一问题,文献[4]中提出了一种被广泛应用的方法。该方法利用外部种群来存储算法当前获得的Pareto最优解集,然后从外部种群中选择合适的个体作为粒子的全局最优位置。而粒子的个体最优位置则为其在历史搜索过程中所找到的最优位置。RAQUEL等[8]提出了一种基于拥挤度距离的多目标粒子群算法。该算法首先基于拥挤度距离和变异算子来保证外部种群的多样性,然后再次利用拥挤度距离从外部种群中选择出个体的全局最优位置。MARTNEZ等[9]提出了一种基于分解的算法dMOPSO。该算法通过分解策略来确定粒子的全局最优位置。
综上所述,大多数的改进算法都是在传统MOPSO的基础上引入各种算子来提高算法的搜索效率的。其中如何保证种群多样性几乎是每种改进算法都必须要考虑的一个关键因素。不同于大多数算法只是利用多样性度量指标评估算法的最终运行结果,文中提出了一种基于多样性控制的MOPSO算法(MOPSO-DC)。该算法在每一次迭代中都监测当前所获得的Pareto最优解集的多样性,并根据多样性度量指标自适应地选择不同的粒子更新策略。论文主要工作如下:
(1) 采用一种基于权值向量的度量指标来评估算法在每次迭代中获得的Pareto最优解集的多样性。
(2) 采用一种基于Steffensen方法的自适应变异算子,以保持种群多样性。
(3) 自适应选择粒子的全局最优位置来实现种群的更新操作。
1 相关工作
1.1 多目标优化问题
以最小化问题为例,一个多目标优化问题可抽象为如下形式:
(1)
其中,x是N维搜索空间中的一个粒子(决策变量),fj(x) (j=1,2,…,M)为 粒子x的第j个目标函数值,M为目标空间的维数。
因为多目标优化问题包含了M个相互排斥的优化目标,因此优化算法无法找到一个可以同时最优化所有目标的最优解。多目标进化算法的目的就是在搜索空间中找到由一组互不支配的个体构成的Pareto最优解集。Pareto支配及Pareto最优解集[10]定义如下。
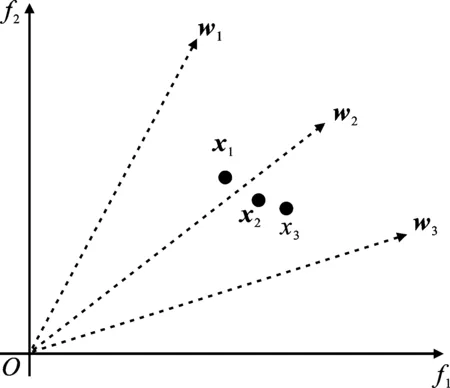
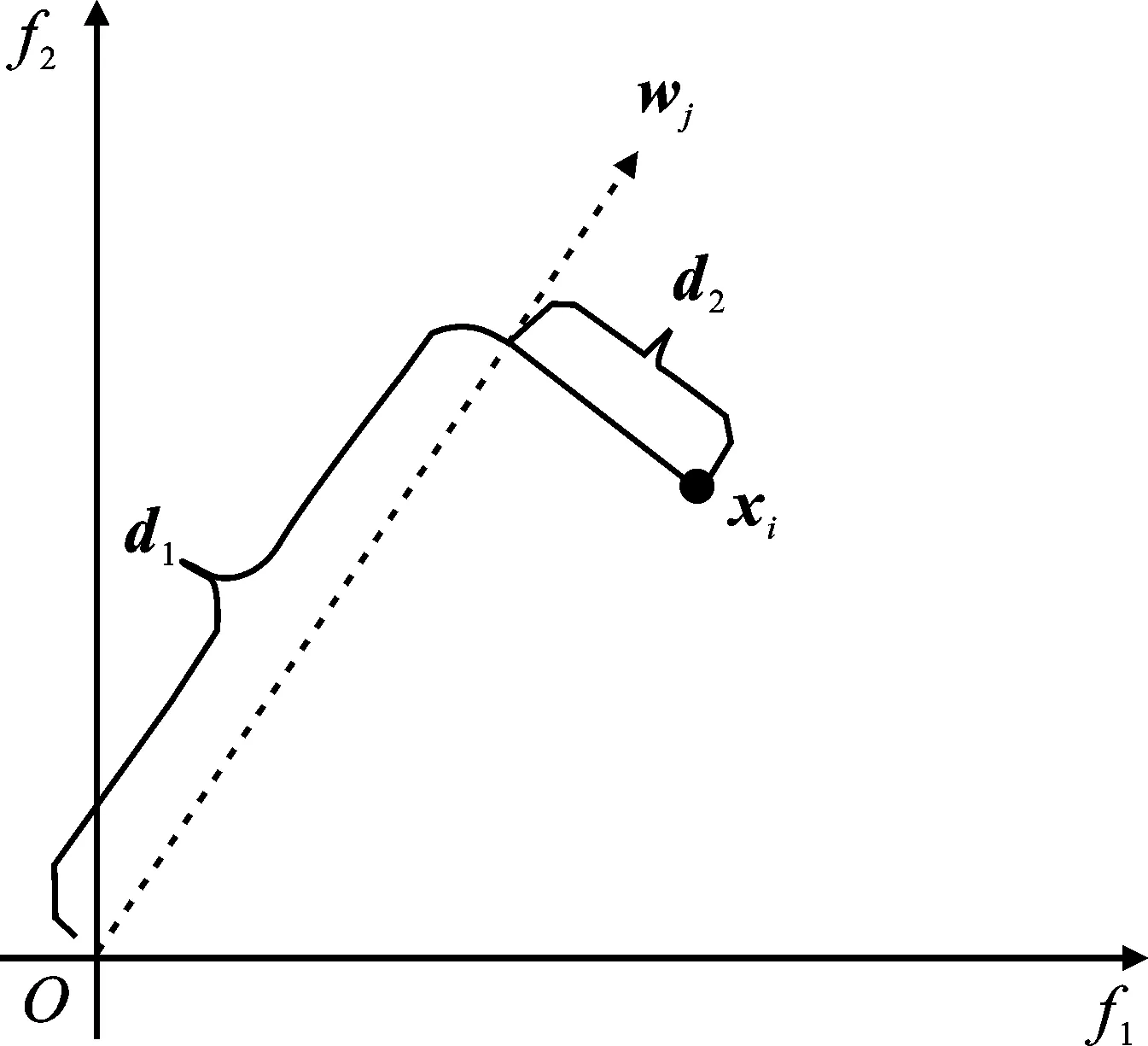
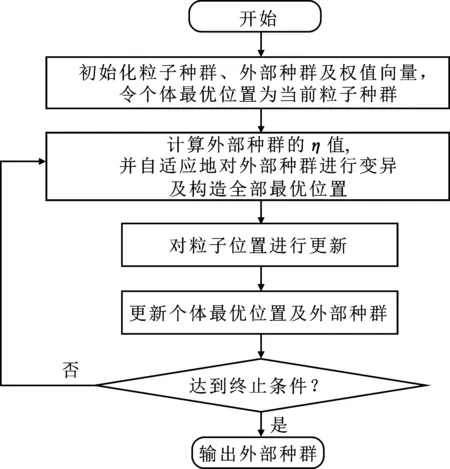
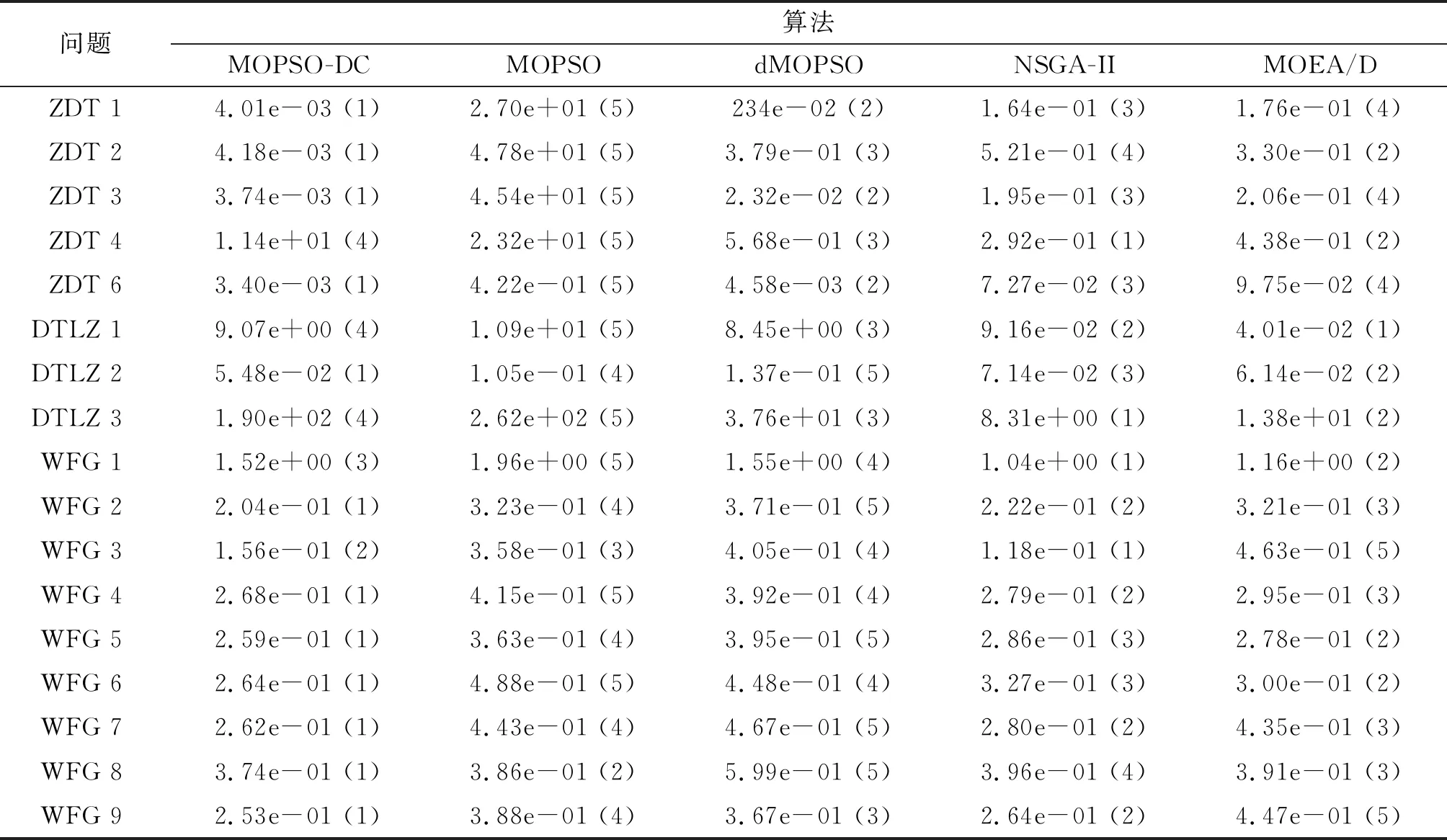
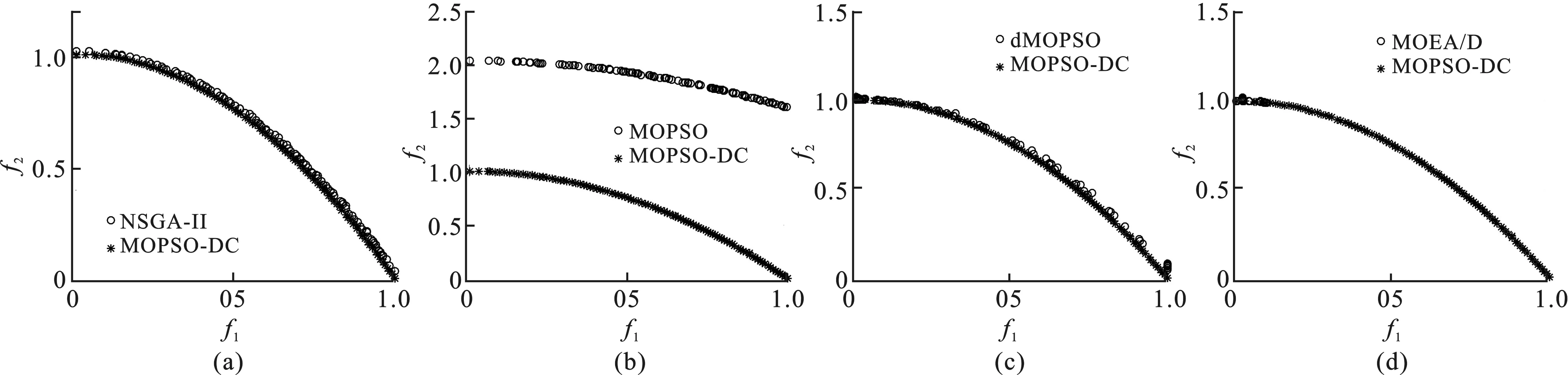
Pareto支配:对于式(1)定义的多目标问题,称搜索空间中的决策变量x1支配x2,即x1≻x2,当且仅当∀j∈{1,2,…,M},fj(x1)≤fj(x2),并且∃j∈{1,2,…,M},fj(x1) Pareto最优解集:对于式(1)定义的多目标问题,若其搜索空间为Ω,则Pareto最优解集P*为 P*:={x∈Ω|∃x′∈Ω,x′≻x}。 (2) MOPSO通过粒子在搜索空间中的移动来搜索Pareto最优解集,其中粒子位置的更新速度受全局及个体最优位置的影响。全局最优位置g记录了整个种群当前搜索到的最优位置,而个体最优位置pi则记录了粒子xi在历史搜索过程中的最优位置。MOPSO中粒子xi的更新过程如下: (3) 其中,t表示算法迭代次数;w为惯性权重,通常取值为0.4;r1与r2为[0,1]区间中取值的随机数,分别表示粒子受个体及全局最优位置影响的程度。 由于多目标优化中无法得到可以同时优化所有目标的最优解,因此粒子个体及全局最优位置的获取也就成了MOPSO算法实现的难点及关键之处。笔者提出了一种基于多样性控制的多目标粒子群算法,通过对算法当前所获得的Pareto最优解集的多样性进行评估,进而根据多样性评估值自适应选择粒子的全局最优位置。 如何寻找非线性方程f(x)=0的根是科学计算中的一个经典问题,而Steffensen方法[11-12]则是被广泛应用的一种非线性方程迭代求根方法。Steffensen方法具体操作可表示为 (4) 其中,x0为初始根值,xk和xk+1分别为第k+1次迭代前及迭代后的根值。 种群多样性是影响多目标进化算法性能的一个重要因素。因此,在算法运行过程中对种群多样性进行实时评估,根据多样性评估值调整种群的更新策略,可有效避免算法陷入早熟。文中提出了一种基于权值向量的多样性评价指标来评估算法在每一次迭代中所获得的Pareto最优解集的多样性。 该评价指标的核心思想即利用一组在目标空间均匀分布的权值向量,通过计算当前算法获得的非支配解集所覆盖的权值向量数目与权值向量总数的比值来评估该非支配解集的分布情况。具体计算过程为 (5) 其中,np为Pareto最优解集覆盖的权值向量数目,nw为权值向量总数。 图1 基于权值向量的多样性 评价指标示意图 图1以两目标优化问题为例,给出了基于权值向量的多样性评价指标的评估示意图,其中w1~w3为一组在目标空间均匀分布的权值向量,x1~x3为算法当前获得的Pareto最优解集(即算法当前外部种群中的个体)。由图1可得,x1、x2、x3在权值向量集合中分别与w2夹角距离最近,因此整个Pareto解集覆盖到了权值向量中的一个向量w2。由式(5)可得,当前η值为1/3。根据如上描述,η取值区间为[0,1]。η值越小,则表明当前Pareto最优解集在目标空间中的分布越集中。 若算法当前获得的Pareto最优解集为P,则对其进行多样性评价的步骤如下: 步骤1 根据DAS等所提方法[13]产生一组在目标空间均匀分布的权值向量{w1,w2,…,wk}。 步骤2 产生一个k维零向量z=[0,0,…,0]。 步骤3 对P中的任一个体xi,计算与其在目标空间中夹角距离最近的权值向量wj,并设置z(j)=1。 步骤4 计算得出多样性指标η=sum(z)/k。 由上述步骤可知,η借助权值向量反映了Pareto最优解集在目标空间的分布情况。η取值范围为[0,1],η取值越大,则说明当前Pareto最优解集的多样性越好。 MOPSO-DC算法利用外部种群存储算法获得的Pareto最优解集,并通过在外部种群中选择合适的个体来作为粒子的全局最优位置。因此,外部种群的多样性会直接影响粒子种群的搜索能力。文中利用一种基于Steffensen方法的变异策略来增加外部种群的多样性。当外部种群的η指标小于给定阈值时,则对外部种群中的个体进行变异。如图2所示,w1~w3为一组在目标空间均匀分布的权值向量,x1~x3为外部种群中的个体。对个体x1,首先从距其最近的几个权值向量中随机选择得出一个权值向量(假设为w1),然后以降低x1与w1之间的距离D(x1,w1)为目标,对x1进行变异得到距离w1更近的变异个体x'1。通过逐一对外部种群中的个体进行如上操作,得到一组在目标空间中分布较均匀的变异个体。 图3 距离D(xi,wj)计算过程示意图 (6) 其中,x'i,k为xi,k经过变异后的值,L(xi,k)=D(xi,wj)-d*。 以外部种群中的某一个体xi为例,其变异操作如下: 步骤1 计算得出与xi夹角距离最近的δ(δ小于权值向量的个数)个权值向量,并从δ个权值向量中随机选择一个权值向量wj。 步骤2 计算xi到wj的距离D(xi,wj)=d1+d2。 步骤3 在xi中随机选择一维(假设为第k维)进行变异。令d*=rD(xi,wj),L(xi,k)=D(xi,wj)-d*,其中r∈(0,1)。则根据式(6),可得出xi,k变异后的值x'i,k。 在MOPSO-DC中,粒子位置的更新借鉴传统的MOPSO算法,根据式(3)来实现。其中,以每个粒子在历史搜索过程中获得的最优位置作为其个体最优位置。而全局最优位置则根据2.1节中获得的η值自适应地从外部种群中进行选择得出。当η值小于等于给定阈值时,则对外部种群中的个体根据拥挤度距离[14]进行排序,从拥挤度距离前10%的个体中随机选择一个个体作为粒子的全局最优位置。当η值大于给定阈值时,首先计算得出与当前粒子xi夹角距离最近的权值向量wj;然后根据2.2节步骤2从外部种群中选择与wj距离最近的非支配个体作为xi的全局最优位置。 图4 MOPSO-DC算法的流程图 图4为MOPSO-DC算法的流程图,其具体操作步骤如下: 步骤1 初始化粒子种群,计算每个粒子的适应度值,并选择粒子种群中的非支配个体作为外部种群,产生一组在目标空间中均匀分布的权值向量W={w1,w2,…,wk},设置种群的个体最优位置为当前粒子种群。 步骤2 计算当前外部种群的η指标。 步骤3 若η小于给定阈值s,则对外部种群中的每个个体进行变异,并从变异后的种群及原外部种群中选择非支配个体作为新的外部种群。 步骤4 根据2.3节及阈值s,自适应地从外部种群中为每个粒子选择全局最优位置。 步骤5 根据式(3)对粒子位置进行更新,并计算其适应度值,并对个体最优位置进行更新。 步骤6 将外部种群更新为算法目前搜索到的非支配个体构成的集合。 步骤7 判断是否满足终止条件,若满足,则输出外部种群;若不满足,则跳转至步骤2进行下一次迭代。 为评估算法性能,文中选取了ZDT1~ZDT4、ZDT6、DTLZ1~DTLZ3、WFG1~WFG9作为测试函数,并选择MOPSO[4]、dMOPSO(MOPSO Based on Decomposition)[9]、NSGA-II(Non-dominated Sorted Genetic Algorithm)[13]、MOEA/D(Multi-objective Evolutionary Algorithm Based on Decomposition)[15]作为对比算法来分析所提出算法的有效性。对MOEA/D,设置大小分别为100(对于2目标问题)和105(对于3目标问题),其余算法的种群大小均为100。对所有算法,最大函数评价次数为10 000。选择逆世代距离(Inverted Generational Distance,IGD)[16]及分布指标(SPacing,SP)[17]作为评价算法性能的量化指标。其中,IGD指标用来度量算法产生的Pareto前沿面与真实的Pareto前沿面之间的距离。当IGD值为零时,则表示算法搜索到了真实Pareto前沿面中的所有个体。SP指标则用来度量算法产生的Pareto解集的分布情况。当SP值为零时,则表示算法搜索到的Pareto最优解集中的个体是均匀分布的。每个算法独立运行30次来获得最终的统计结果。算法的具体参数设置见表1。 表1 算法的参数设置 MOPSO-DC中,参数s用来控制粒子全局最优位置的选择。若s取值过小,则算法将会耗费大量的计算量用于保持外部种群的多样性,有时候甚至可能引起搜索的退化;若s取值过大,则可能会造成多样性,保持效果较差,算法陷入早熟。因此,为了选择合适的s取值,以ZDT1、ZDT4、DTLZ2及IGD指标为例,来分析s的不同取值对算法性能的影响。表2给出了MOPSO-DC在不同s取值下30次运行的平均IGD值。其中,当s取值为0.7时,算法针对ZDT1和DTLZ2均取得了最优的IGD值。对于ZDT4,s取值为0.5和0.7时,算法分别取得了最优及第二优的IGD值。因此,在文中将阈值s设置为0.7。 表3和表4为5种算法针对不同测试问题经过30次独立运行的平均IGD值与SP值。其中括号中的数值为算法在不同测试函数上的排序值,排序值为1则表明该算法在所有算法中针对给定的测试函数表现最好。 根据表3和表4中的统计结果,MOPSO-DC在所有测试函数上的IGD值均优于MOPSO的,且在大多数测试函数上的SP值优于MOPSO的。这说明了MOPSO-DC中所提出策略的有效性。MOPSO-DC中的基于权值向量的多样性评价指标、基于Steffensen方法的自适应变异策略以及自适应粒子更新策略,能够有效平衡算法的收敛性及种群多样性,从而提高了算法的搜索效率。 表3 算法针对不同测试问题的平均IGD值 表4 算法针对不同测试问题的平均SP值 图5~图7分别给出了文中算法与对比算法在ZDT 2、ZDT 4、DTLZ 2、WFG 2、WFG 4、WFG 6以及WFG 8上的Pareto前沿面。 图5 MOPSO-DC与对比算法在ZDT 2函数上的Pareto前沿面 对于函数ZDT 4,MOPSO-DC在IGD指标及SP指标上的表现均要差于dMOPSO和MOEA/D。 对于函数DTLZ 1和DTLZ 3,MOPSO-DC在IGD指标及SP指标上的表现均要差于NSGA-II及MOEA/D。这是由于MOPSO-DC利用自适应粒子更新策略根据计算得出的多样性评价指标及给定阈值,来判断是否对外部种群进行变异以及对粒子选择拥挤度距离较大的全局最优位置,这在一定程度上影响了算法跳出局部最优的能力。因此,算法在处理某些多峰问题时性能差于对比算法,图6中5种算法在ZDT 4上的Pareto前沿面也验证了上述结论。 表5给出了算法在针对所有测试函数的平均排序结果。其中,MOPSO-DC在IGD指标和SP指标均取得了最优排序值,这说明虽然MOPSO-DC在某些函数上效果不佳,但综合所有测试函数来考虑,MOPSO-DC取得了最好的结果。 表5 算法平均排序值 算法在WFG系列测试函数上的统计结果表明,MOPSO-DC对于绝大多数WFG测试函数都取得了最优的IGD值,对WFG 1、WFG 3、WF 5及WFG 6上取得了最优SP值。对于WFG 4、WFG 7~WFG 9,MOPSO-DC取得的平均SP结果差于MOPSO。这是由于MOPSO-DC采用的变异策略首先对于变异后的个体进行评价,然后从变异后的个体与原始外部种群中选择非支配个体作为新的外部种群。与传统的变异策略相比,笔者所提变异策略需要耗费一定的函数评价次数。此外,为了保证变异后的个体向着Pareto前沿面靠拢,MOPSO-DC选择变异个体与原始外部种群中的非支配个体作为新的外部种群,因此有时会造成某些分布较好的变异个体不会被保留,导致算法对于一些测试问题获得的非支配解集SP指标差于对比算法。图8~图11分别给出了MOPSO-DC与对比算法在WFG 2、WFG 4、WFG 6、WFG 8上的Pareto前沿面。以MOPSO-DC与MOPSO的对比图为例,从图中可以看出,MOPSO-DC获得的Pareto最优解集更接近理想的Pareto前沿面,但是MOPSO所获得Pareto最优解集分布更均匀。 图8 MOPSO-DC与对比算法在WFG 2函数上的Pareto前沿面 针对传统MOPSO算法容易早熟的问题,笔者提出了一种基于多样性控制的多目标粒子群算法(MOPSO-DC)。该算法在每一次迭代中都对外部种群的多样性进行评估,并根据评估值自适应地选择是否对外部种群进行变异操作以及选择不同的粒子种群更新方式。对比实验表明,MOPSO-DC与传统MOPSO算法相比,展现了很强的优势,且与其他对比算法相比,也表现出了很强的竞争性。但实验结果同样展现了MOPSO-DC存在一些不足。一方面,在MOPSO-DC采用的基于Steffensen方法的自适应变异策略中,只有当变异个体为非支配个体时才会被保留,这可能造成算法在耗费计算量的同时,不会提升其所获得的Pareto解集的分布性;另一方面,MOPSO-DC利用自适应粒子更新策略,根据计算得出的多样性评价指标及给定阈值,来判断是否对外部种群进行变异,以及对粒子选择拥挤度距离较大的全局最优位置,这在一定程度上影响了算法跳出局部最优的能力。因此,如何更有效利用获得的变异个体及增强算法在处理多峰问题时跳出局部最优的能力,是未来的一个研究方向。1.2 MOPSO算法
1.3 Steffensen方法
2 MOPSO-DC算法设计
2.1 基于权值向量的多样性评价指标
2.2 基于Steffensen方法的自适应变异策略
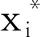
2.3 自适应粒子更新策略
2.4 MOPSO-DC算法流程
3 实验分析

3.1 参数分析
3.2 对比实验结果与分析


4 结束语

