多桥墩沉降下轨道底座板与桥面板间脱空区域的研究分析
陈天浩, 杨建伟, 王金海, 金 京
(1.北京建筑大学 机电与车辆工程学院, 北京 100044;2.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室, 北京 100044)
到2025年,以“八纵八横”为主要通道的高铁共计3.8万km,将覆盖中国的主要居住区。随着铁路网络覆盖范围的拓展,高速火车和铁路的运营将涉及许多恶劣环境。高速铁路[1]的大部分里程采用桥梁,桥梁会经受各种变形,如桥墩沉降和桥梁体徐变等。桥梁变形在火车的周期性载荷、混凝土徐变效应等因素下随时间不断积累,会显著影响轨道规则性和车辆动力响应。为确保安全操作和高速列车的乘坐舒适性,有必要研究桥梁变形对轨道系统的影响。

图1 纵连板式轨道结构底座板随桥墩沉降脱空情况Fig.1 Situation of void area of the base plate along with pier settlement in the longitudinal connected ballastless track system
吴楠等[2]分析了桥墩沉降、横向变形以及桥梁跨径减少等不同桥梁变形模式对高速铁路车辆运行的影响,并且提出了相应的限制。徐庆元等[3]通过建立车辆- 轨道- 桥梁的有限元模型,研究了墩台沉降不均匀对车辆的动力响应,发现其与轨道系统各部件间、底座板与桥面板间的脱空有关。刘传、杨建伟等[4-6]建立城轨列车模型,研究了牵引和制动工况下,桥梁徐变上拱对车辆的动力响应,发现城轨车辆脱轨系数受到明显影响,最大影响范围不超过50%。石晓宇[7]结合桥墩沉降与桥梁徐变上拱2种工况,研究了其对高速列车行车安全的影响。李志强等[8]分析了列车在单墩、相邻两墩和相邻三墩沉降3种情况下的列车动力响应,发现相邻三墩沉降时,车辆竖向加速度最大。陈兆伟等[9-11]推导出了桥墩沉降和钢轨垂向变形之间的映射表达式,分析了单元板式和纵连板式轨道条件下,不同沉降量对钢轨变形的影响,并用有限元模型加以验证。蔡小培等[12]通过建立有限元模型,研究了路基沉降对双块式无砟轨道平顺性的影响。肖威等[13]针对路基的余弦不平顺,通过有限元模型得出底座板和路基之间的接触力、脱空区域随沉降量增大而增大。尽管有上述进展,但大多数都是通过有限元模型方式进行的仿真,尚未有文献研究桥墩沉降和底座板脱空区域的关系。
为了研究桥墩沉降和底座板脱空区域的关系,本文开展了单墩沉降、相邻两墩沉降和相邻三墩沉降3种工况下不同沉降量的脱空区域范围大小对比分析。
1 底座板脱空的机理分析
简支梁桥发生桥墩沉降时,沉降桥墩相邻的两跨梁桥在重力的作用下产生垂向位移,梁上的轨道结构也随之发生相应变形。图1所示为纵连板式轨道条件下,轨道底座板与桥面板的脱空区域示意图。
轨道底座板与其上部结构在重力作用下发生垂向位移,同时因为轨道底座板的纵向联结特性,导致轨道底座板与桥面板之间产生脱空区A、B、C和接触区P、Q。P处是由桥墩沉降带动的桥梁转动抬起所致,Q处是由重力引起的垂向位移大于梁体位移所致。由此可见,沉降量的大小对脱空区域和接触区域的大小有直接影响。
2 沉降值与脱空区域的映射关系
2.1 底座板位移表达式
为得到单墩沉降引起的底座板脱空区域范围,本文导出了单墩沉降与脱空区域的映射关系。为研究底座板与桥面板间的脱空区域,因此将底座板- 砂浆层- 轨道板- 钢轨简化成一个整体,根据简支梁的挠度公式,底座板的位移矩阵Zp为:
Zp=GGp-HFp
(1)
式中:G和H分别为重力Gp和接触力Fp对底座板变形的作用效果矩阵。
矩阵G与矩阵H形式相同,矩阵G中的元素表达式为:
(2)
式中:Ep为底座板的弹性模量,单位为Pa;Ip为底座板截面惯量,单位为m4;lp为底座板长度,单位为m;Xp,j为第j个底座板单元距离底座板左端的距离,单位为m。
第i个底座板与桥面板单元间的接触力Fp,i为:
Fp,i=kb,i(Zp,i-Zb,i)
(3)
式中:Zp,i为第i个底座板单元的垂向位移,单位为m;Zb,i为第i个桥面板单元的垂向位移,单位为m;kb,i为第i个底座板与桥面板单元间的接触刚度,单位为N/m。
其中:
(4)
式中:kb为底座板与桥面板的接触刚度值,单位为N/m。
因此,接触力Fp为:
Fp=Kb(Zp-Zb)
(5)
式中:Kb为接触力刚度矩阵;Zb为桥面板位移矩阵。
2.2 桥墩沉降引起的桥面板位移表达式
在单墩沉降模型中,沉降量d为唯一变量。但在多墩沉降模型中,各墩的沉降量均为变量,使得计算更加复杂。梁位移与墩沉降的几何关系如图2、图3所示。图2和图3分别为单墩沉降和多墩沉降时梁体位移示意,lb1为梁端到支座的距离,单位为m;lb0为梁上两支座间的距离,单位为m;di与di+1分别为不同的沉降量,单位为mm。

图2 第i跨梁体位移(单墩沉降)Fig.2 Displacement diagram of ind span beam (in the single pier settlement model)

图3 第i跨梁体位移(多墩沉降)Fig.3 Displacement diagram of ind span beam(in the multi-pier settlement model)
单墩沉降时,沿桥梁的纵向,每个单元处的桥梁位移Zb,i为:
Zb,i=(xb,i-lb1)×d/lb0
(6)
式中:xb,i为第二跨梁上第i个桥梁单元距左端的距离,单位为m。
多墩沉降下桥梁位移公式同理也可得出,故不再详细列出。
2.3 沉降值与脱空区域的映射关系
底座板和桥面板的脱空区域范围通过如下步骤循环迭代求解:
步骤1,假设底座板和桥面板初始是全接触,则对于i=1~n,都有kb,i=kb,其中n为底座板与桥面板的单元数。
步骤2,联立式(1)式(3)和式(5)可以求出Zp,i和Zb,i,并判断Zp,i和Zb,i的大小。如果Zp,i>Zb,i,则i点对应的位置为接触区域;反之则为脱空区域。并令kb,i=0;
步骤3,循环步骤2,直到接触力刚度矩阵Kb稳定,即可得到Kb矩阵。并且通过底座板位移矩阵Zp和桥面板位移矩阵Zb对比得出脱空区域的范围。
2.4 脱空区域映射关系的有限元验证
在ABAQUS中建立轨道- 桥梁系统有限元模型,得到该系统随桥墩沉降而产生的脱空区域范围的数值解,以此来验证脱空区域范围的解析表达式。考虑到模型的结构对称性,取一半的结构进行建模分析,如图4所示。

图4 轨道- 桥梁有限元模型Fig.4 Simulation model of track-bridge
在该模型中,桥面板和底座板、底座板和砂浆层、砂浆层和轨道板之间采用表面- 表面的接触方式,轨道板和钢轨之间的接触关系用绑定约束的方式,各部件弹性模量参数见表1。

表1 有限元模型中各部件的弹性模量参数
计算时,每跨桥梁长度为32.60 m,分别取4跨和5跨,沉降量d均取30 mm,用有限元模型得出的底座板位移大小对解析表达式得到的结果进行验证,验证结果如图5、图6所示。

图5 单墩沉降底座板位移Fig.5 Displacement of base plate under the single pier settlement

图6 相邻两墩沉降底座板位移Fig.6 Displacement of base plate under the two adjacent piers settlement
由于底座板的纵向联结特性,随着中部桥墩沉降的产生,底座板随之产生垂向变形,在进入沉降区域时,底座板会稍微上翘,这是由于中部沉降导致梁体转动,两端因此被抬起。在沉降区域,底座板位移均达到最大值,且有缓和过渡曲线。由有限元模型和解析模型得出的底座板位移基本拟合,说明解析模型完全可以用于求解纵连板式轨道结构下桥墩沉降引起的底座板脱空区域的范围尺寸。相比有限元模型,解析模型更容易表现出轨道系统各参数之间的关系,而且建模更加方便,下文将采用解析模型来分析不同沉降对底座板脱空区域的影响。
3 不同沉降工况对脱空区域的影响分析
3.1 单墩沉降工况下,沉降量对脱空区域的影响分析
每跨桥梁长度为32.60 m,沉降量d分别取5 mm、10 mm、15 mm、20 mm、25 mm、30 mm和35 mm,底座板与桥面板间的间隙大小如图7所示。

图7 不同沉降量下底座板到桥面板的间距Fig.7 Distance between base plate and bridge plate under different settlement
由图7可知,桥墩沉降引起的底座板脱空区域一共有5处,分别位于3号桥墩(里程=65.20 m)处以及2号(里程=32.60 m)和4号桥墩(里程=97.80 m)相邻的左右位置,脱空区域的大小呈对称状,故取2号桥墩左右位置和3号桥墩处的脱空区域范围进行详细阐述,如图8、图9所示。

图8 2号桥墩左右位置处底座板到桥面板的间距Fig.8 Distance between base plate and bridgeplate at the left and right positions of No.2 pier
在2号桥墩左右位置处,脱空区域存在于桥墩处左边里程29.00~32.00 m、右边里程33.00~36.00 m,桥墩里程32.00~33.00 m为接触区。这是由于3号桥墩沉降,底座板在重力作用下产生垂向位移,引起梁体的转动,使得底座板在2号桥墩附近位置有少量上挠。同时,桥梁由于3号桥墩沉降而下沉,桥梁转动使第二跨桥梁的左端点处(即2号桥墩处)有少许抬起,使得该桥墩位置的桥梁与底座板相接触。由图8所示,脱空区域的范围和底座板与桥面板的间距随沉降量增加而增加。

图9 3号桥墩处底座板到桥面板的间距Fig.9 Distance between base plate and bridgeplate at the No. 3 pier
如图9所示,在沉降发生处(里程=65.20 m),脱空区域范围和底座板与桥面板的间距随沉降量的增大而增大,呈对称结构,最大间距发生在沉降处(里程=65.20 m),不同沉降量对应的脱空区域范围和最大间距的具体数据见表2。

表2 不同沉降量的脱空区域参数
由表2可得,脱空区域的范围大小随沉降量增加而增加,但随着沉降量的增加,范围大小的增加量逐渐减少;底座板与桥面板的间距随沉降量增加而增加,并且最大间距值的变化量随着沉降量增加而增加。原因是底座板由于纵向联结特性,在刚度可承受范围内随着沉降量的增加,变形会达到一个最大值,达到这个限制后,脱空区域范围大小不再随沉降量增加有明显变化。
3.2 相邻两墩沉降工况下,沉降量对脱空区域的影响分析

图10 相邻两墩不同沉降量下底座板与桥面板的间距Fig.10 Distance between base plate and bridgeplate of two adjacent piers under different settlements

图11 脱空区域局部放大Fig.11 Partial enlarged view of the void area
由于地基松软且范围较大,不只会产生单墩沉降。因此,相邻双墩同时沉降时,底座板与桥面板间产生的脱空区域如图10所示。图10中,取桥长为163.00 m,桥跨距为32.60 m。在3号(里程=65.20 m)和4号(里程=97.80 m)桥墩处同时发生沉降,沉降量d分别为20 mm、25 mm、30 mm和35 mm。图11(a)、图11(b)分别为图10中2号桥墩(里程=32.60 m)和3号桥墩(里程=65.20 m)处的局部放大图。
由图10可知,相邻两墩发生相同沉降量时,引起的脱空区域有6处,且脱空区域范围和间距大小随沉降量的增大而增大,呈对称结构,最大间距发生在沉降的两桥墩处。当沉降量为35 mm时,最大间距为0.30 mm,相比于单墩沉降35 mm时的最大间距值,减少了70%。
当相邻两墩沉降量不同时,令i、j分别表示3号和4号桥墩的沉降量,分别取i=35 mm、j=25 mm和i=35 mm、j=30 mm,沉降结果如图12所示。θj1和θj2分别表示2种不同沉降量下,4号桥墩相邻梁的夹角。对脱空区域进行对比分析,结果如图13所示。

图12 相邻两墩沉降示意Fig.12 Schematic diagram of settlement of two adjacent piers
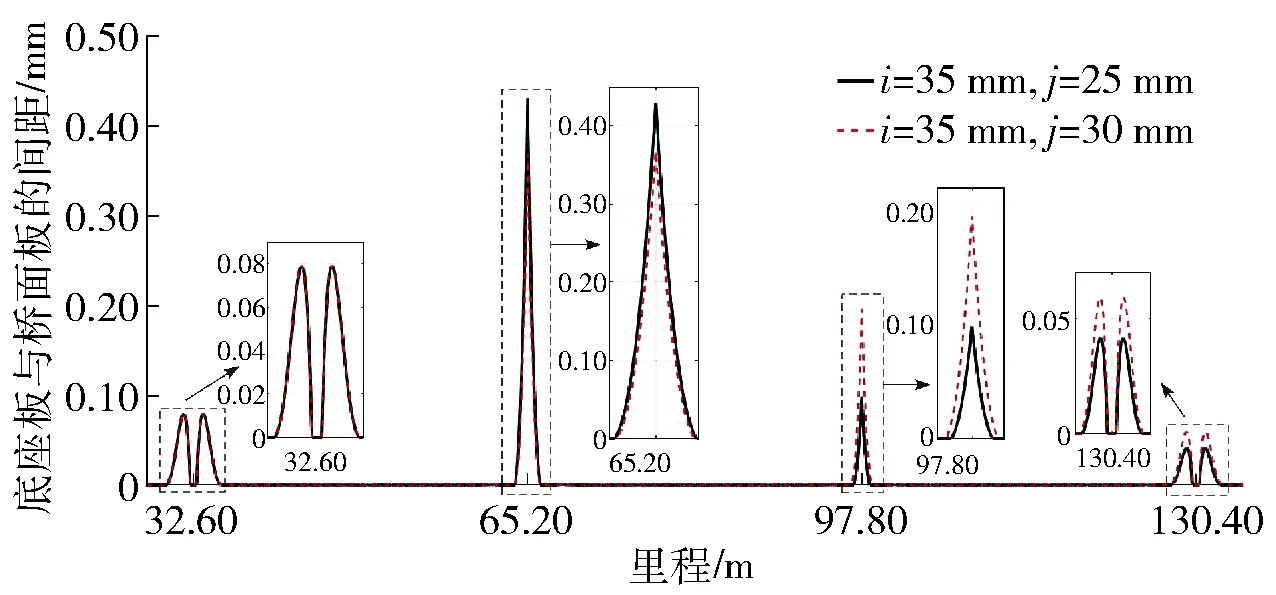
图13 脱空区域局部放大Fig.13 Partial enlarged view of the void area
由图12和13可得,当相邻两墩发生不同沉降时,引起的脱空区域为6处,最大脱空间距发生在最大沉降量处。通过对比2组数据,结合图12可得,桥墩沉降处相邻的两跨梁夹角越小,脱空间距越大。
3.3 相邻三墩沉降工况下,沉降量对脱空区域的影响分析
为进一步讨论大范围桥墩沉降对脱空区域的影响,对相邻三墩沉降时沉降量对脱空区域的影响进行分析。取桥长为195.60 m,桥跨距为32.60 m,3号、4号和5号桥墩的沉降量分别为i、j、k。沉降示意如图14所示。

图14 相邻三墩沉降示意Fig.14 Settlement diagram of adjacent three piers
由于不同墩的沉降量之间存在不确定关系,因此分3种情况讨论。
当相邻三墩沉降量i=j=k=30 mm时,脱空区域与里程的关系如15所示。

图15 三墩沉降量为30 mm时脱空区域示意Fig.15 Schematic diagram of the void area when the settlement value is 30 mm
由图15可知,三墩沉降引起的脱空区域一共为6处。因为相邻三墩沉降量均为30 mm,所以4号桥墩处左右两边的跨梁夹角为180°,呈水平状,因此在4号桥墩(里程=97.80 m)沉降处的脱空间距值为0。脱空区域产生在3号(里程=65.20 m)和5号(里程=130.40 m)桥墩跨梁夹角处。
当最大沉降量发生在相邻三墩的中间时,即里程=97.80 m处沉降量最大,沉降结果如图16所示。
通过对比图16(a)~(d)在5号桥墩处(里程=130.40 m)的间距值可得,桥墩沉降处相邻的两跨梁夹角越小,脱空间距越大。
当最大沉降值发生在相邻三墩的一侧时,沉降结果如图17所示。
通过对比图17(a)和图17(b)在4号桥墩(里程=97.80 m)处脱空区域间距值可得,该处相邻两跨梁夹角越大,脱空间距越小,且夹角越接近180°,间距大小越接近于0。

图17 相邻三墩不同沉降量对比Fig.17 Comparison of different settlements of adjacent three piers
同时,通过对比图16、图17可以得出,某一桥墩的沉降量产生变化,只会对相邻桥墩的脱空区域间距值产生影响。如图16、图17所示,5号桥墩(里程=130.40 m)处沉降量的变化对不相邻的2号桥墩(里程=32.60 m)的间距值没有影响。
4 结论
本文对纵连板式轨道条件下桥墩沉降量与底座板脱空区域的关系进行了推导,计算了底座板随桥墩沉降的位移曲线,并加以有限元验证,同时还对单墩、相邻两墩和相邻三墩沉降工况下,不同沉降量产生的底座板脱空区域变化进行了对比分析。主要结论如下:
1)桥墩沉降时,底座板和桥面板会发生局部脱离,形成脱空区域。由桥墩沉降量与底座板脱空区域的映射关系推导的解析模型可用于求解底座板脱空区域问题。
2)单墩沉降工况中,脱空区域范围和脱空最大间距值随沉降量的增加而增加,但是脱空区域范围的增加量逐渐减小,而间距的增加量逐渐增大。相同沉降量下,单墩沉降的脱空区域最大间距值远大于多墩沉降的最大间距值。
3)在相邻两墩和三墩沉降工况中,桥墩沉降处相邻的两跨梁夹角越小,脱空间距值越大。当夹角趋向于180°时,间距值趋向于0。在多墩沉降中,某一桥墩的沉降量产生变化,只会对相邻桥墩的脱空区域间距值产生影响。

