齿轮磁流体润滑与动力学耦合研究
菅光霄, 王优强*, 于 晓, 李云凯, 罗 恒
(1.青岛理工大学 机械与汽车工程学院,山东 青岛 266520;2.青岛理工大学 工业流体节能与污染控制教育部重点实验室,山东 青岛 266520)
磁流体作为一种智能润滑材料,由基载液、磁性颗粒及表面活性剂组成.它既有固体材料的磁性,又有液体的流动性.在磁场作用下,磁流体可以准确地充满润滑表面实现连续润滑,从而延长齿轮的使用寿命.近年来,国内外学者在磁流体技术与应用方面开展了大量卓有成效的工作,取得了不错的研究成果.Shah等[1]分析了颗粒旋转、各向异性磁导率和滑移速度对多孔渗透挤压薄膜轴承承载能力和中心压力位置的影响,并运用Neuringer-Rosensweig、Jenkins 和Shliomis三种模型,在均匀和非均匀磁场下进行了长轴颈轴承挤压膜特性的对比研究,发现非均匀磁场比均匀磁场能产生更大的承载力.Osman等[2]以非牛顿流体研究了磁流体润滑轴承的动静态特性,探讨了磁场参数对磁流体润滑轴承承载能力和摩擦系数等的影响.Vashi等[3]基于Neuringer-Rosensweig模型,计入滑移速度、应力偶效应、表面粗糙度和磁场强度的作用,研究了磁流体挤压膜的性能.Hsu等[4]的研究表明适当的表面粗糙度和磁场可以减小摩擦系数,提高磁流体润滑轴承的承载能力.Laghrabli等[5]基于Shliomis模型,研究了使用磁流体作为润滑剂的有限长径向滑动轴承的静态性能.Shukla等[6]的研究表明磁性纳米颗粒的旋转运动能够改变磁流体的黏度,进而影响其润滑性能.史修江等[7]考虑热效应、载荷时变效应、非牛顿效应、不同基载液及磁场强度的影响,研究了磁流体润滑滑动轴承的润滑性能.
在齿轮流体润滑的理论研究方面,部分学者[8-9]考虑了表面粗糙度特征对齿面润滑的影响,并对齿轮的疲劳寿命进行了预估.赵晶晶等[10-11]基于简化的静载荷模型,分析了冲击载荷作用下磁流体润滑齿轮的膜厚和压力分布,但忽略了动载荷的影响.事实上,多数关于齿轮瞬态弹流润滑的计算均没有考虑齿轮振动所引起的动载荷及轮齿表面速度波动的影响,而是以简化的静载荷模型进行计算.部分学者考虑了振动或冲击对齿轮润滑的影响,如Xue等[12]基于齿轮的时变啮合刚度,利用数值模拟的方法,分析了动载荷对油膜厚度、油膜压力以及油膜温升的影响.邹玉静等[13]基于载荷分担理论与动力学理论,对渐开线直齿轮的弹流润滑特性与动力学特性进行了耦合研究.Cruz等[14]基于摩擦动力学模型,进行了多轴齿轮传动系统的瞬态热混合润滑分析,发现油膜压力及油膜厚度的振荡能够加剧齿轮振动及噪声的产生.苑士华等[15-17]综合考虑油膜润滑和齿面摩擦效应,基于载荷分担理论建立齿轮系统动力学模型,研究了不同转速对渐开线齿轮动载荷的影响.
对于磁流体润滑的齿轮,磁流体黏度受外加磁场的影响.磁流体黏度的变化会改变齿面润滑效果及轮齿间的动载荷分布.综上所述,本文作者建立齿轮的磁流体润滑模型,在进行润滑理论的研究时,将润滑模型与齿轮的动力学模型相结合,进行齿轮磁流体润滑与动力学的耦合研究,分析齿面的润滑特性以及磁流体润滑对渐开线直齿轮动载荷分布的影响.
1 齿轮动力学模型
考虑齿轮时变啮合刚度的影响,建立齿轮动力学模型,该模型仅考虑直齿圆柱齿轮的扭转振动.如图1所示,其中y轴沿啮合线方向.图中Ip、Ig;θp、θg;Tp、Tg分别表示主动轮和从动轮的转动惯量、扭转角位移和转矩(下标p和g分别代表主动轮和从动轮).km和cm分别表示啮合刚度和啮合阻尼.et为静态传递误差.

Fig.1 The dynamic model of spur gears图1 齿轮动力学模型
在研究过程中,未考虑齿轮的制造和几何误差,而主要考察了齿轮系统的刚度激励作用以及载荷的变化,故认为静态传递误差为零,只存在动态传递误差.
齿轮系统的动态传递误差为

动态啮合力为
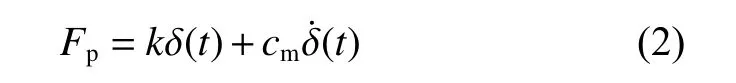
由齿轮系统的动力学模型,建立其动力学微分方程[18]为
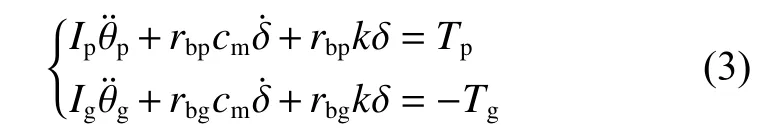
式中:k为综合刚度,是齿轮啮合刚度与油膜刚度的耦合值.
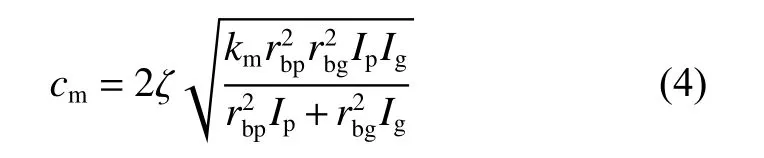
式中:ζ为阻尼比,根据K L WANG等[19]的研究,ζ的值一般为0.03~0.17,本文中取值ζ =0.1.
综合刚度的计算公式为

式中:kh为油膜刚度.
部分学者对油膜刚度的计算进行了相关研究[20-21],本文中采用的油膜刚度的计算公式[22-24]为

式中:hc为中心油膜厚度.
采用Weber能量法[25],求解齿轮的时变啮合刚度.利用四阶Runge-Kutta 法求解动力学微分方程.
根据渐开线的性质,两齿轮在任意啮合点处的瞬时曲率半径为
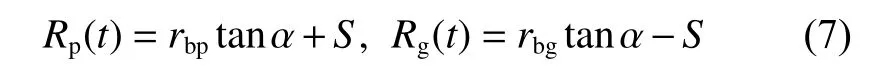
式中:α为分度圆压力角;rbp和rbg分别为主、从动轮的基圆半径;S为啮合点到节点的距离.
两齿轮在任意啮合点处的综合曲率半径[26]为
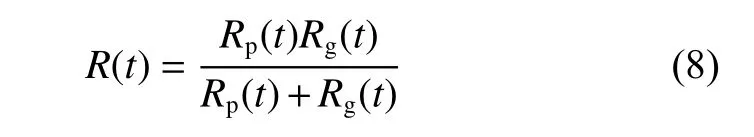
振动会引起轮齿表面速度的波动,两轮齿表面的切向速度[27]为
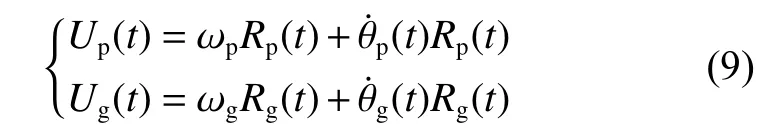
式中:Up和Ug分别为主、从动轮表面的切向速度,两者的后一项表示由于振动引起的齿轮表面速度的波动值.
两当量圆柱的卷吸速度为
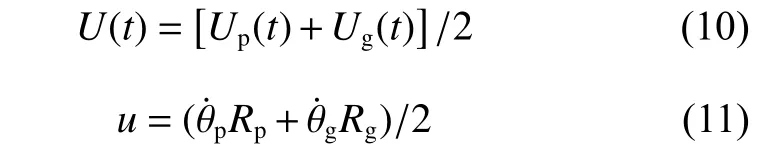
式中:U为卷吸速度,u为齿轮副振动速度,表征由振动所引起的卷吸速度的波动值.
2 润滑模型
2.1 Reynolds 方程
考虑外磁场作用、热效应以及时变效应的无限长线接触的Reynolds方程[28]为
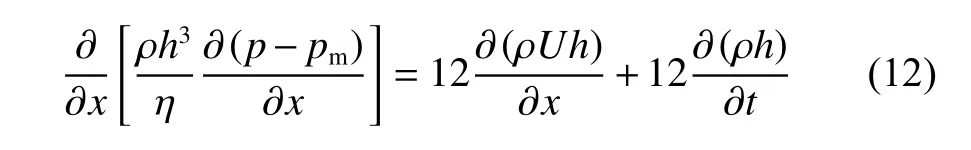
式中:ρ和 η分 别为磁流体的密度和黏度;p和h分别为油膜压力和油膜厚度;pm为磁场力.
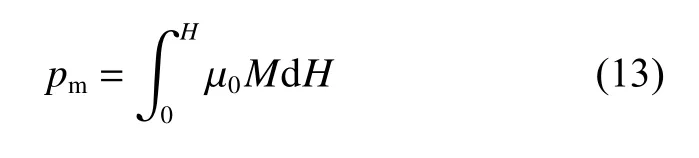
式中:M为磁化强度;H为磁场强度.

µ0为真空磁导率,µ0=4π×10−7H/m,B为磁感应强度.
求解Reynolds方程所使用的边界条件为
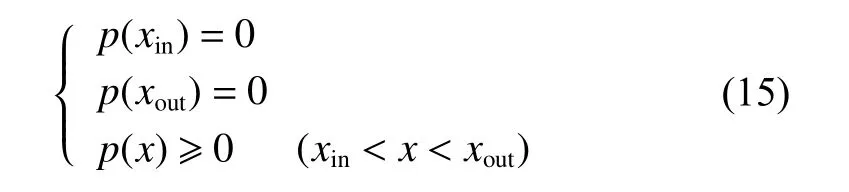
式中:xin=-4.6b,xout=1.4b;b为赫兹接触区半宽.
2.2 黏度方程
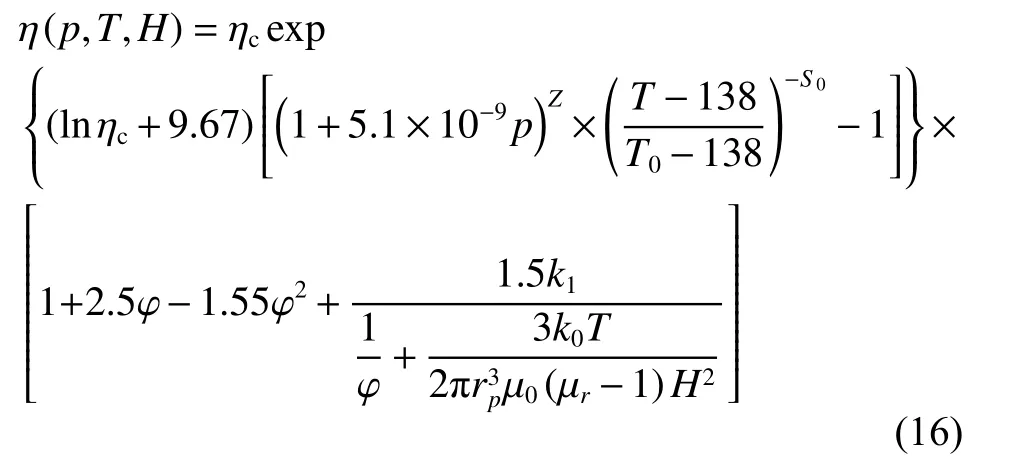
式中: η0为T0温度下基载液的黏度,T0=313 K;Z和S0分别为黏压系数和黏温系数;rp为磁性颗粒的平均半径;k1为实验与理论黏度增量的比例系数,通常取0.5~3;φ为磁性颗粒的体积分数;k0为玻尔兹曼常数,k0=1.38×10−23N·m/K.
2.3 密度方程
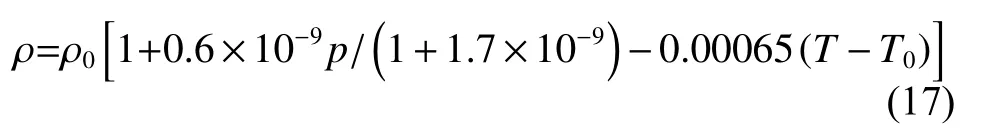
式中:ρ0为环境压力下磁流体的密度.
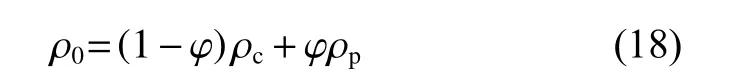
式中:ρc和 ρp分别为基载液和磁性颗粒的密度.
2.4 膜厚方程
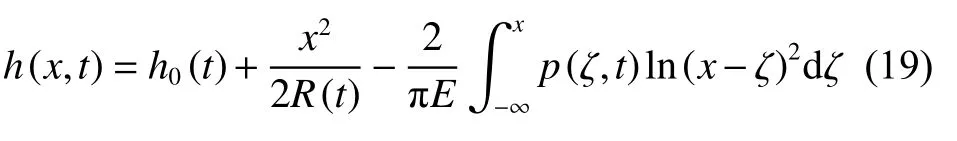
2.5 载荷方程
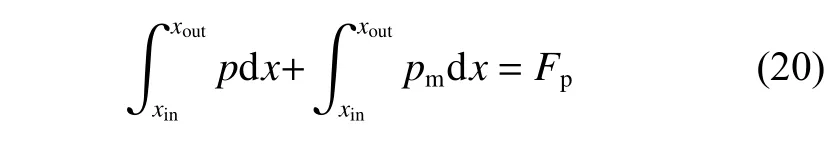
2.6 能量方程

式中:c为磁流体的比热容;k为磁流体的热传导系数;u*为磁流体的流速,其计算方法由文献[11]给出.
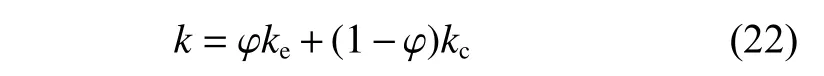
式中:ke和kc分别为Fe3O4磁性颗粒和基载液的热传导系数.
3 数值方法
进行齿轮磁流体润滑与动力学耦合研究的示意图如图2所示.
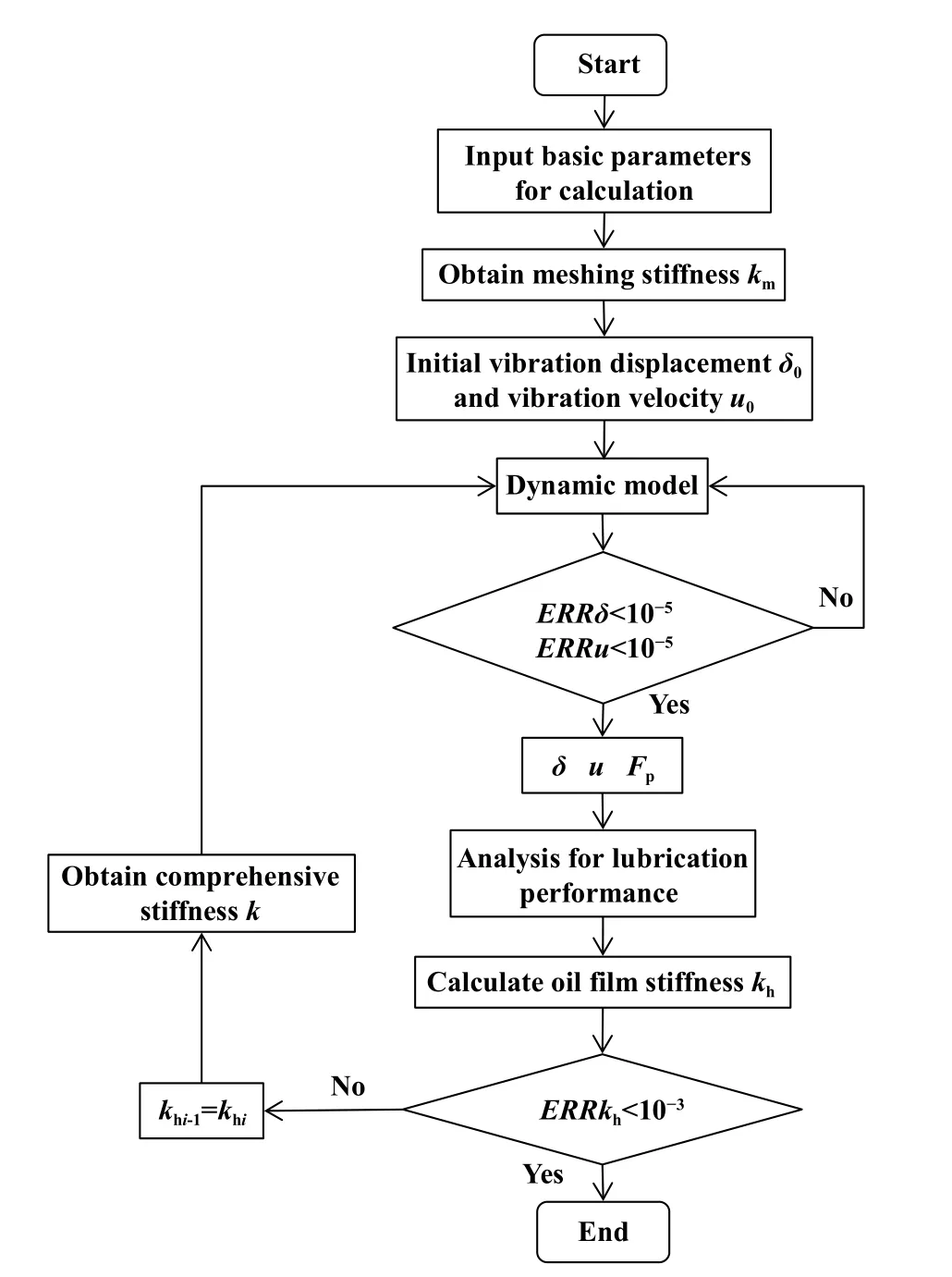
Fig.2 The flow chart for calculation图2 计算流程图
首先进行动力学模型求解,利用四阶Runge-Kutta法求解动力学微分方程,获得动态啮合力和齿轮副振动速度,代入润滑模型进行分析.基于润滑模型的求解结果,计算油膜刚度后得到综合刚度,分析油膜润滑对动力学特性的影响.
作为一种新颖的润滑剂材料,磁流体中磁性颗粒的粒径只有5~10 nm,比表面粗糙度细的多,一般不会引起磨损[29].本文中选取Fe3O4磁性颗粒的质量分数为5%的铁磁流体进行研究,磁性颗粒的半径rp=5 nm.将润滑模型中涉及的基本方程量纲一化并进行离散化处理后,进行齿轮的润滑求解.采用多重网格法求解油膜压力,油膜厚度的求解则采用多重网格积分法[30].利用多重网格法进行油膜压力的迭代时,采用W循环,将网格划分为6层,每层网格的节点数分别为31、61、121、241、481和961.设定压力的计算域xin=−4.6b,xout=1.4b.在每层网格上均使用Guass-Sedial进行压力的低松弛迭代,将齿轮啮合的1个周期划分为180个瞬时,每一瞬时压力计算的迭代初值使用前一瞬时压力迭代的结果.迭代收敛判据为每个瞬时压力和载荷的相对误差小于0.001.
如图2所示,ERRδ、ERRu和ERRkh分别为动态传递误差、齿轮副振动速度以及油膜刚度的相对误差.三者所对应的收敛判据为
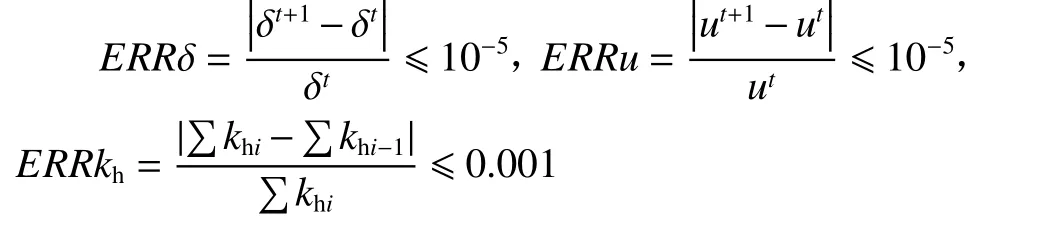
4 结果与讨论
用于计算和分析的齿轮传动的基本参数列于表1中.

表1 齿轮传动和润滑的基本参数Table 1 Basic parameters of gear transmission and lubrication
4.1 磁场对磁流体黏度的影响
图3为不同磁感应强度下磁流体黏度的变化曲线.外磁场作用时,随着磁感应强度的增大,磁流体的黏度先增大;在磁感应强度达到35 mT左右时,继续增大磁感应强度,磁流体的黏度将达到1个稳定值.这是因为磁流体中的磁性颗粒达到了饱和磁化强度,其在宏观上的表现为磁流体黏度的稳定性.
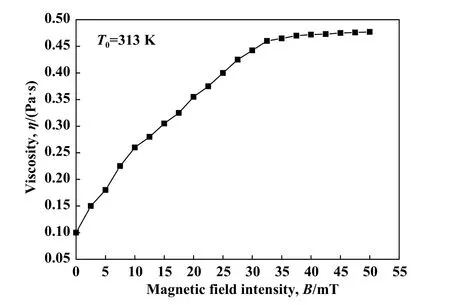
Fig.3 The viscosity for ferrofluid图3 磁流体黏度变化曲线
4.2 磁场对油膜刚度的影响
图4 为磁场作用下节点处油膜刚度的变化曲线.与磁流体黏度的变化相似,随着磁感应强度的增大,磁流体的黏度增大,润滑剂分子间距离减小,分子间斥力增大,油膜难以被压缩,其在宏观上的表现为油膜刚度的增大;当磁性颗粒达到饱和磁化强度后,磁流体的黏度达到稳定,继续增大磁感应强度,油膜刚度达到稳定.
图5为无磁场作用以及磁感应强度为15、25、35和45 mT磁场作用下的油膜刚度的时变曲线,所选取的是齿轮啮合的1个周期.如图5所示,在单齿啮合区内,由于只有1对齿承载,润滑剂分子间距离小,分子间斥力大,油膜难以被压缩,因而单对齿啮合时的油膜刚度远大于双齿啮合时油膜刚度的数值;当磁感应强度达到35 mT时,继续增大磁感应强度,油膜刚度的变化不明显.
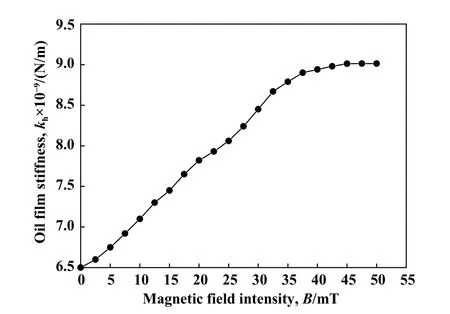
Fig.4 The oil film stiffness at the pitch point图4 节点处油膜刚度变化曲线
4.3 动力学特性分析
油膜刚度是齿轮系统动力学与润滑实现联接的“桥梁”,由于齿轮啮合刚度与油膜刚度均具有时变性,因此,将图5所计算的时变油膜刚度与齿轮啮合刚度耦合,得到综合刚度,结果如图6所示.随着磁感应强度的增大,综合刚度不断增大,当磁感应强度达到35 mT时,磁流体中的磁性颗粒已基本达到饱和磁化强度,此时继续增大磁感应强度,综合刚度的变化很小.
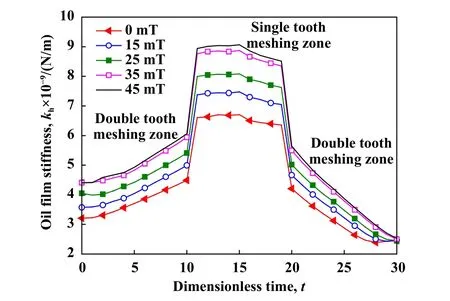
Fig.5 The time-varying oil film stiffness图5 油膜刚度的时变曲线

Fig.6 The time-varying comprehensive stiffness图6 综合刚度的时变曲线

Fig.7 The vibration characteristic of gear system图7 齿轮系统的振动特性曲线
图7 为基于动力学模型所求解的齿轮系统的振动特性曲线,主要反映动态传递误差和齿轮副振动速度的变化.从图7中可以看出,动态传递误差和齿轮副振动速度均呈现出衰减振荡的变化趋势,在单双齿啮合的交替点(图6所示的B、D两点),动态传递误差和齿轮副振动速度均存在跃变,这是由单双齿啮合交替所导致的综合刚度的跃变而引起的.与单齿啮合区相比,在双齿啮合区内,动态传递误差和齿轮副振动速度的波动值较小,齿轮传动的平稳性更好.这是因为在双齿啮合区内,两对齿同时承载,综合刚度大,因而动态传递误差和齿轮副振动速度较小.
从图7中可以看出,随着外磁场磁感应强度的逐渐增加,动态传递误差和齿轮副振动速度的波动值呈现出逐渐减小的趋势,当磁感应强度达到35 mT时,若继续增大磁感应强度,动态传递误差和齿轮副振动速度的变化不明显.这表明适当增加磁场强度并使磁性颗粒达到其饱和磁化强度,可以改善齿轮传动的稳定性.
图8所示为基于动力学模型所求解的齿轮系统的动载荷谱,它反映了轮齿间动态啮合力的变化.横坐标S表示啮合点到节点的距离,S=0为节点的位置.在啮入点(A点)和单双齿啮合的临界点(B、D点),存在明显的啮入冲击和换齿冲击.随着外磁场磁感应强度的增大,动载荷的幅值减小并且趋于稳定的速度加快,啮入冲击和换齿冲击得到改善.
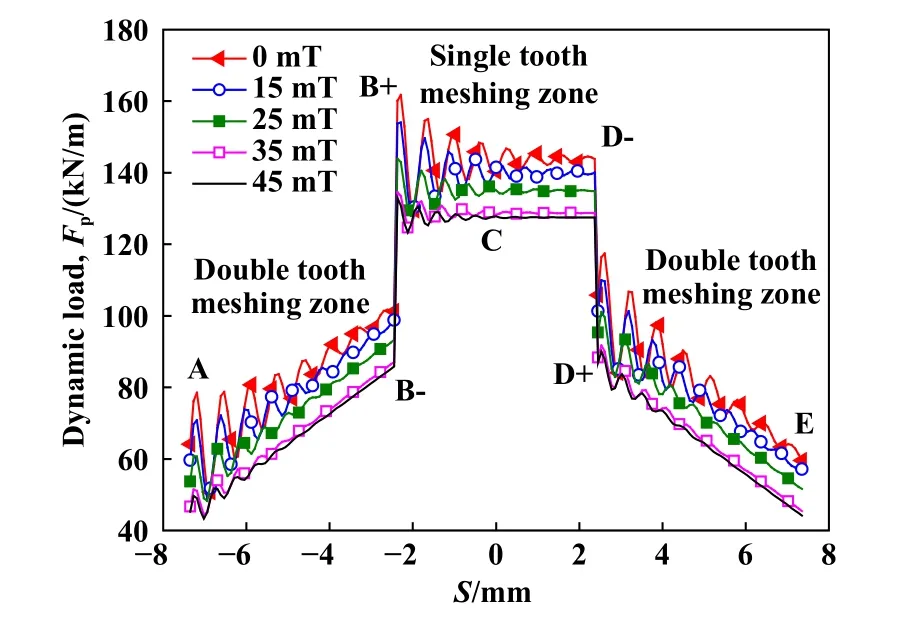
Fig.8 The dynamic load spectrum of the gear system图8 齿轮系统的动载荷谱
4.4 润滑特性分析
图9 所示为中心油膜压力曲线.受动载荷的影响,中心油膜压力也呈现出明显的衰减振荡的变化趋势.随着外磁场磁感应强度的增大,油膜压力减小且趋于稳定的速度加快.
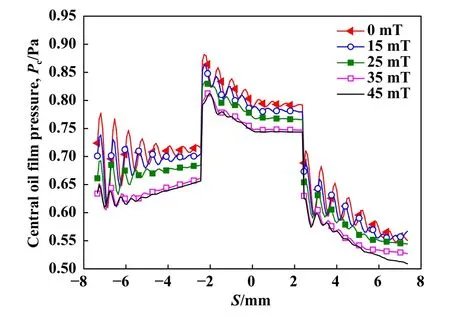
Fig.9 The central oil film pressure图9 中心油膜压力曲线
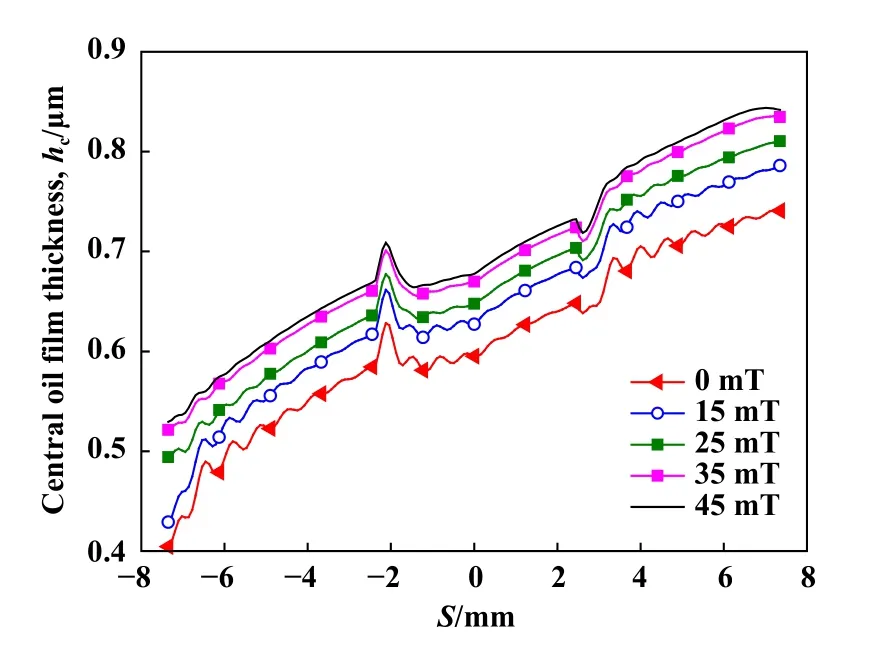
Fig.10 The central oil film thickness图10 中心油膜厚度曲线
图10 为中心油膜厚度曲线.磁感应强度的增大使磁流体的黏度先增大后趋于稳定.因此,随着磁感应强度的增大,中心油膜厚度先增大;当磁感应强度达到35 mT时,继续增大磁感应强度,中心油膜厚度的变化并不明显.动载荷作用下,中心油膜厚度会产生微弱的振荡,其振幅随着啮合点的推移逐渐减小.磁感应强度的增大不仅会增大中心油膜厚度,还使其振幅减小,趋于稳定的速度加快.根据Cruz等[11]的研究,油膜压力和油膜厚度的振荡能够加剧齿轮的振动并产生噪声.因此,适当增大外磁场磁感应强度并使磁性颗粒达到其饱和磁化强度,可以在一定程度上抑制齿轮系统振动和噪声的产生.
图11为齿轮啮出点的瞬态温升分布图.随着磁场强度的增加,中心油膜厚度增加,同时,根据式(19)可知,磁性颗粒的存在增加了磁流体热传导系数,油膜的温升降低.
5 结论
a.外磁场作用下,随着磁感应强度的增大,磁流体的黏度和油膜刚度先增大;当磁流体中的磁性颗粒达到其饱和磁化强度后,磁流体的黏度和油膜刚度趋于稳定.
b.外磁场作用下,适当增大磁感应强度可以改善齿轮系统的传动的稳定性,减小动态传递误差和齿轮副振动速度,减小动载荷,啮入冲击和换齿冲击得到改善.

Fig.11 Transient temperature rise distribution diagram at the recess point图11 啮出点瞬态温升分布图
c.动载荷作用下,中心油膜压力和中心油膜厚度都会呈现出衰减振荡的变化趋势,较大的磁感应强度可以改善油膜温升和增大油膜厚度,使油膜压力和油膜厚度的振幅减小且趋于稳定的速度加快.适当增大外磁场磁感应强度并使磁性颗粒达到其饱和磁化强度,可以在改善润滑效果的同时并在一定程度上抑制齿轮系统振动和噪声的产生.

