减振橡胶疲劳黏滞生热的仿真分析

罗文波, 姜 侠, 胡小玲, 黄友剑

(1. 湘潭大学 岩土力学与工程安全湖南省重点实验室，湖南 湘潭 411105;2. 湘潭大学 土木工程与力学学院，湖南 湘潭 411105)

1 试验

1.1 材料

试验所用橡胶材料由中车株洲时代新材料科技股份有限公司提供。材料基本配方为:100 phr 天然橡胶(泰国RSS3)、20 phr炭黑(N550)、10 phr氧化锌、5 phr抗氧化剂、2.5 phr硫磺、2 phr硬脂酸、2 phr微晶蜡、2 phr固体古马隆、1.4 phr硫化活化剂。

1.2 疲劳生热测试

为了试验测得材料在疲劳载荷作用下的黏滞生热规律，在环境温度为28.5℃以及不同载荷频率和载荷幅值条件下，采用Gabo Eplexor 500 N动态黏弹谱仪对直径10 mm高10 mm的圆柱试样施加正弦波形循环应变。试样受到20%的静态压缩应变和应变幅值分别为1%、2%、3%、4%和5%的动态应变作用，载荷频率分别为10 Hz、30 Hz、50 Hz和70 Hz。循环加载过程中，利用ThermaCAM SC3000红外热像仪对试样表面温度进行实时测温，记录温度随时间的变化过程，热像仪的热灵敏度<0.02℃(30℃时)，测温精度为读数范围的±2%或±2℃。试样和测试设备，如图1所示。

图1 试样与试验设备

图2为加载频率为50 Hz时不同动态应变幅值条件下试样表面的温升历程曲线，图3为给定动态应变幅值为5%时，不同载荷频率条件下试样表面温升历程曲线。可见由于黏滞损耗引起的自热温升随载荷频率和动态应变幅值的提高而增大，在给定载荷频率和动态应变幅值时，试验初期试样表面温度上升较快，随时间逐渐达到稳态平衡值。

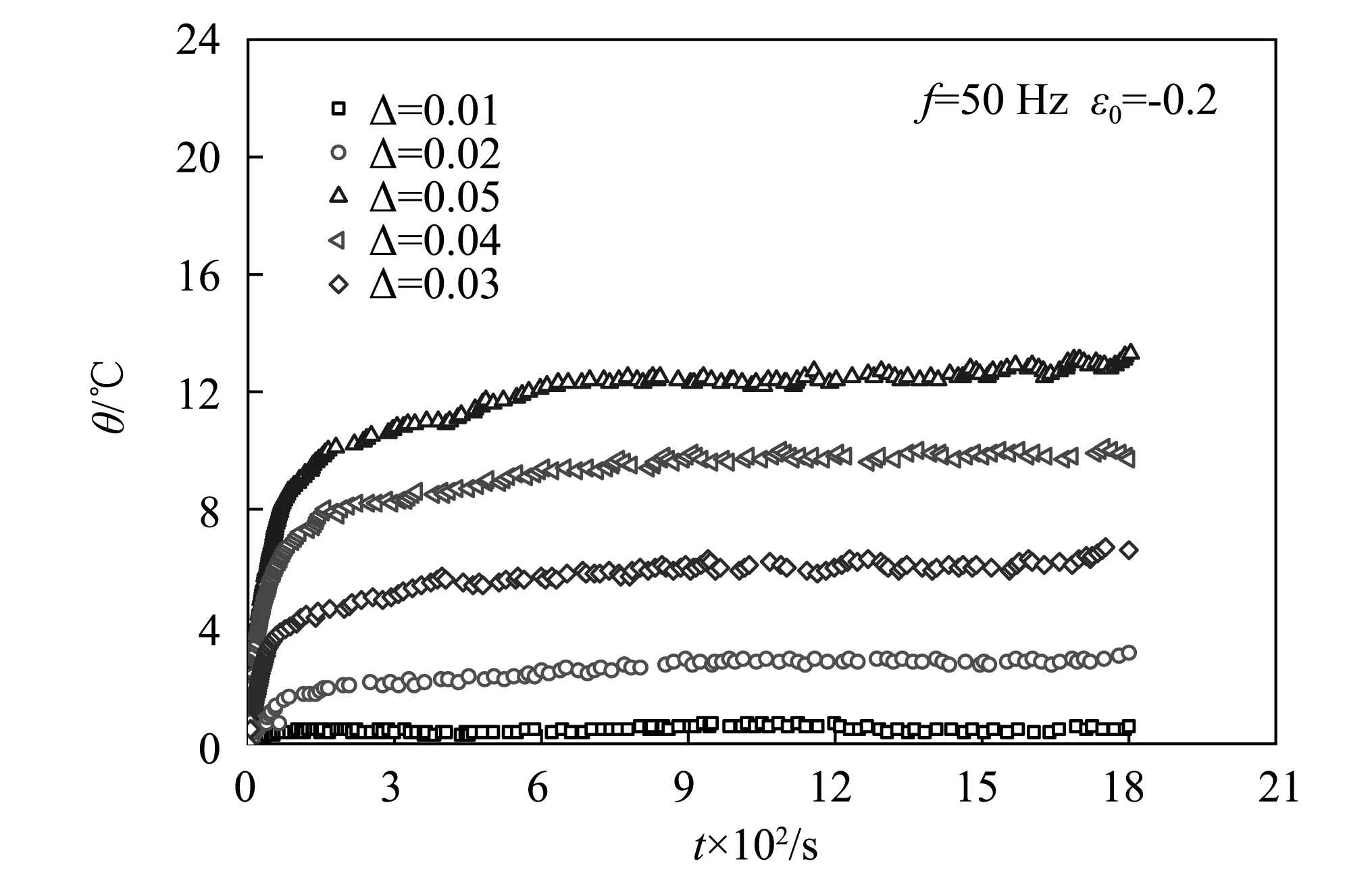
图2 不同应变幅值下的温升曲线

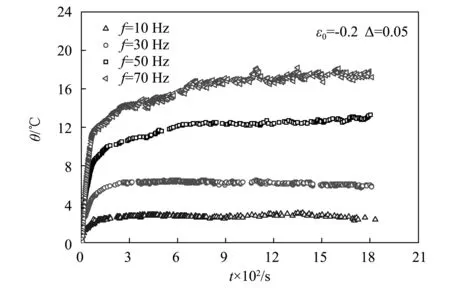
图3 不同载荷频率下的温升历程曲线

2 理论模型

2.1 温度场控制方程

由热力学第一定律和第二定律，黏弹性材料变形过程的温度场控制方程为

(1)

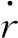
(2)

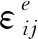
由于橡胶材料具有黏弹性，循环变形过程的应力-应变曲线形成滞回圈，滞回圈的面积即为一个周期变形中单位体积的黏滞耗散热，由下式给出：

3.4 纤毛虫病。1985年前后，生产种苗的牙鲆稚鱼中发生了一种纤毛虫寄生虫病，该病引起了养殖鱼类的大量死亡。

(3)

在应变控制模式下给橡胶材料施加动态应变

ε(t)=ε0+Δsin(ωt)

(4)

式中：ε0为预加的平均应变，Δ为动态应变幅值，ω=2πf为载荷频率。由于材料的黏弹特性，其应力响应与应变存在滞后相位角δ，可表示为：

σ(t)=σ0+E*Δsin(ωt+δ)=σ0+Δ[E′sin(ωt)+E″cos(ωt)]

(5)

式中：E*为复模量，E′=E*cosδ为存储模量，E″=E*sinδ为损耗模量。将式(4)和(5)代入式(3)，有

D=πΔ2E″

(6)

可见，只要确定材料损耗模量E″，就可以求出单位时间单位体积的黏滞耗散热，即能量耗散率密度为：

(7)

2.2 损耗模量的频率和应变幅值相关性

橡胶材料在循环加载过程中，存储模量通常随应变幅值增加逐渐减小，损耗模量和损耗正切随应变幅值增加先增大后减小，这种现象称为Payne效应[16-18]。Kraus模型给出了给定频率和温度下损耗模量随动态应变幅值的变化规律[19-20]

(8)

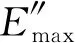
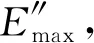
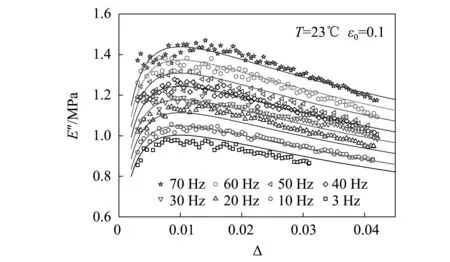
图4 不同频率下损耗模量的Payne效应及其Kraus模型曲线

(9)

2.3 损耗模量的温度相关性

在一定的温度范围内，橡胶材料是热流变简单材料，其力学性能与温度相关[22]。胡小玲等研究表明，无论是存储模量还是损耗模量，在双对数坐标系中，不同温度下动态模量随应变幅值的变化曲线彼此平行，说明各曲线之间沿对数模量坐标轴平移后会彼此重合，存在垂直移位关系，移位因子用lgφT表示，则温度T下的损耗模量E″(T,Δ,f)可以通过参考温度下T0的损耗模量表示为[23]：

E″(T,Δ,f)=φTE″(T0,Δ,f)

(10)

图5是试验橡胶材料在10℃～50℃下Payne效应的测试结果，以T0=20℃为参考温度，不同温度对应的垂直移位因子如图6，在图示温度范围内，损耗模量垂直移位因子的温度相关性可用指数函数表示为：

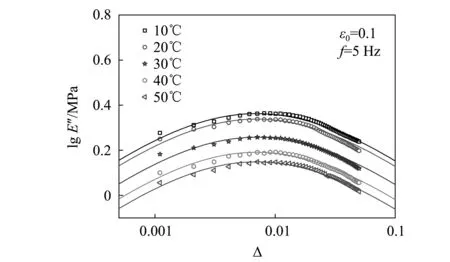
图5 不同温度下橡胶材料的Payne效应

图6 不同温度下损耗模量的垂直移位因子

φT=exp[-0.014(T-T0)],T≥0℃

(11)

综合式(10)和式(11)，试验橡胶材料的损耗模量与载荷频率、幅值、温度的函数关系可以表示为：

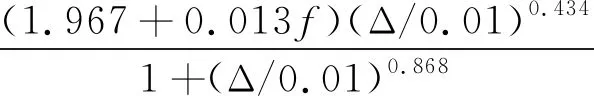
(12)

将式(12)代入式(7)，得橡胶材料单位体积的黏滞生热率为

(13)

3 有限元仿真

3.1 仿真分析流程

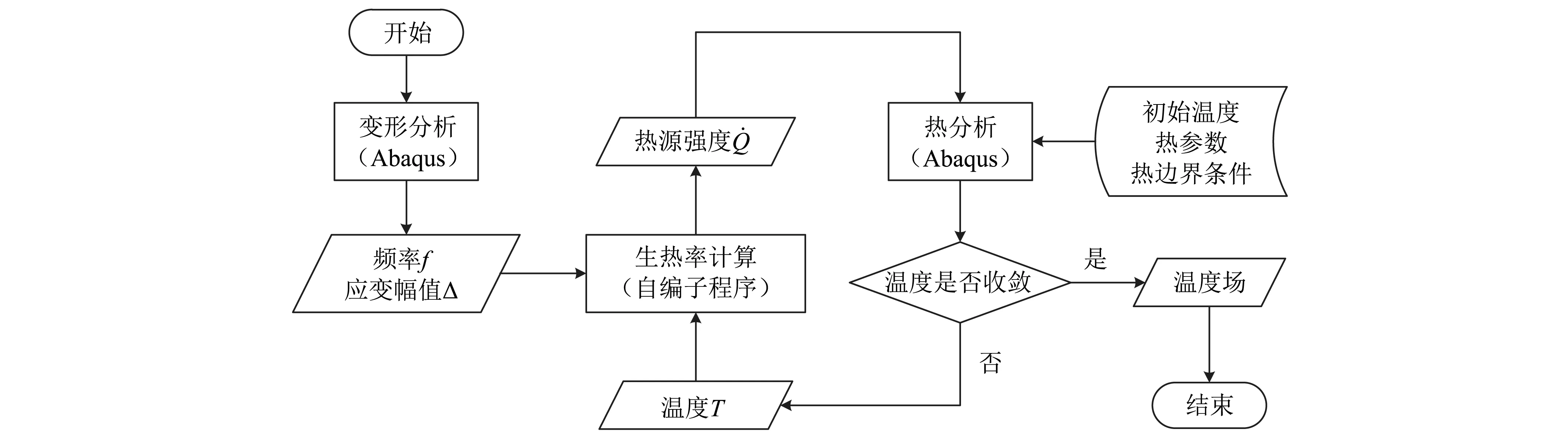
图7 黏滞生热仿真分析流程图

3.2 橡胶超弹性本构模型

在黏滞生热的热力耦合仿真分析过程中需要求解结构在给定载荷下的应变场，因此需要选择合适的材料本构模型。Ogden超弹性模型是应用最广的橡胶材料本构模型之一，其应变能函数[24]为：

(14)

式中：λ1、λ2、λ3是主拉伸比，模型参数μn，αn根据试验数据确定。图8是23℃条件下橡胶材料单轴拉伸(ST)、平面拉伸(PT)和等双轴拉伸(ET)的应力-拉伸比曲线，采用三阶Ogden模型拟合试验结果，得到模型参数为μ1=0.904，μ2=-1.924×10-10，μ3=3.185×10-4，α1=1.063，α2=-17.7，α3=2.380。

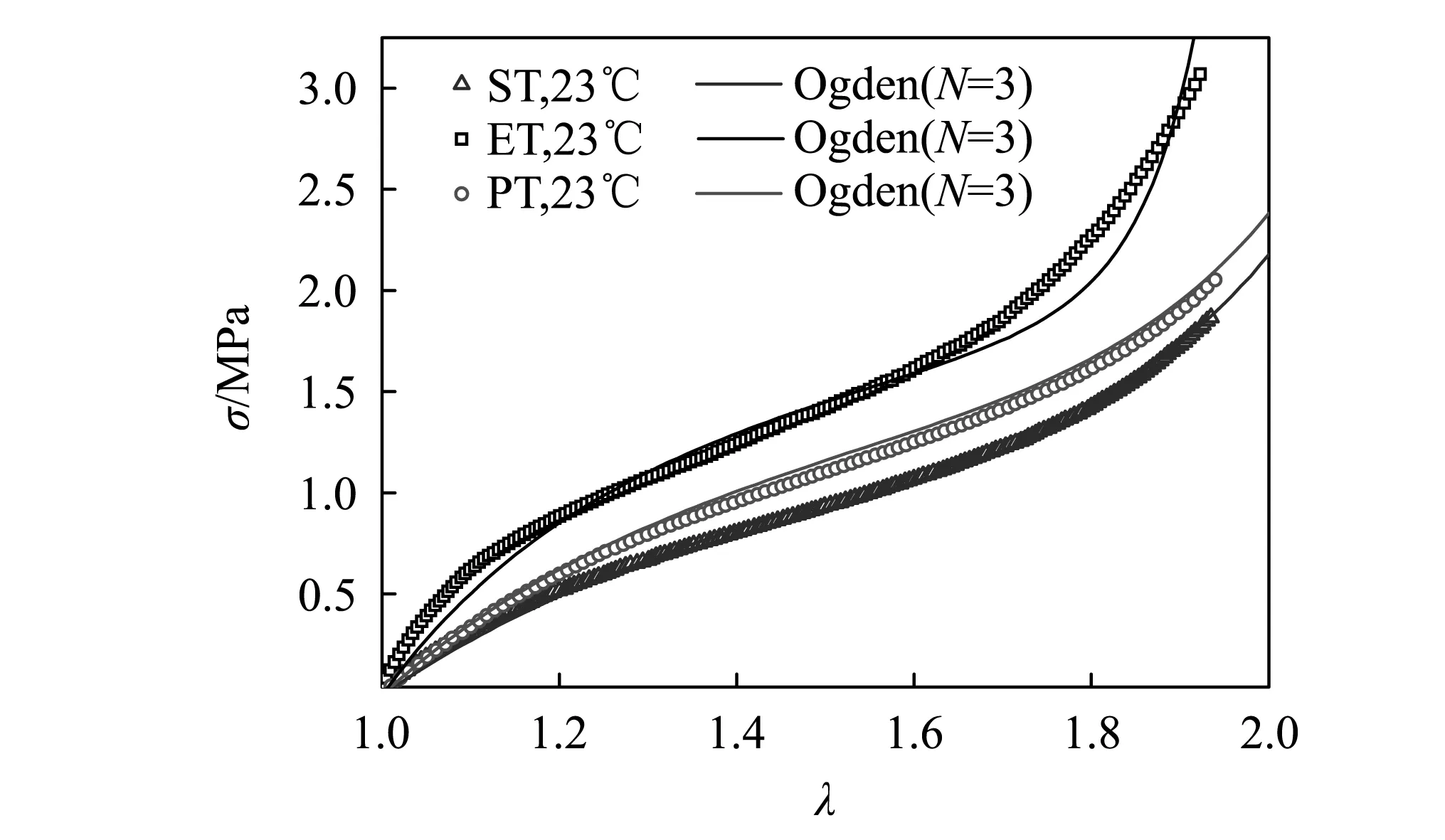
图8 橡胶材料单轴拉伸、平面拉伸和等双轴拉伸应力-拉伸比曲线与Ogden模型描述

3.3 橡胶圆柱试样动态压缩过程的黏滞生热仿真分析

下面对2.2节的橡胶圆柱试样循环压缩的黏滞生热过程进行仿真分析，并将仿真结果与试验测量进行比较，以验证上述热力耦合分析方法的有效性。圆柱试样的有限元网格及热力边界条件如图9所示，选用CAX4HT单元类型，模型参数见表1，参数值取自文献[7]。

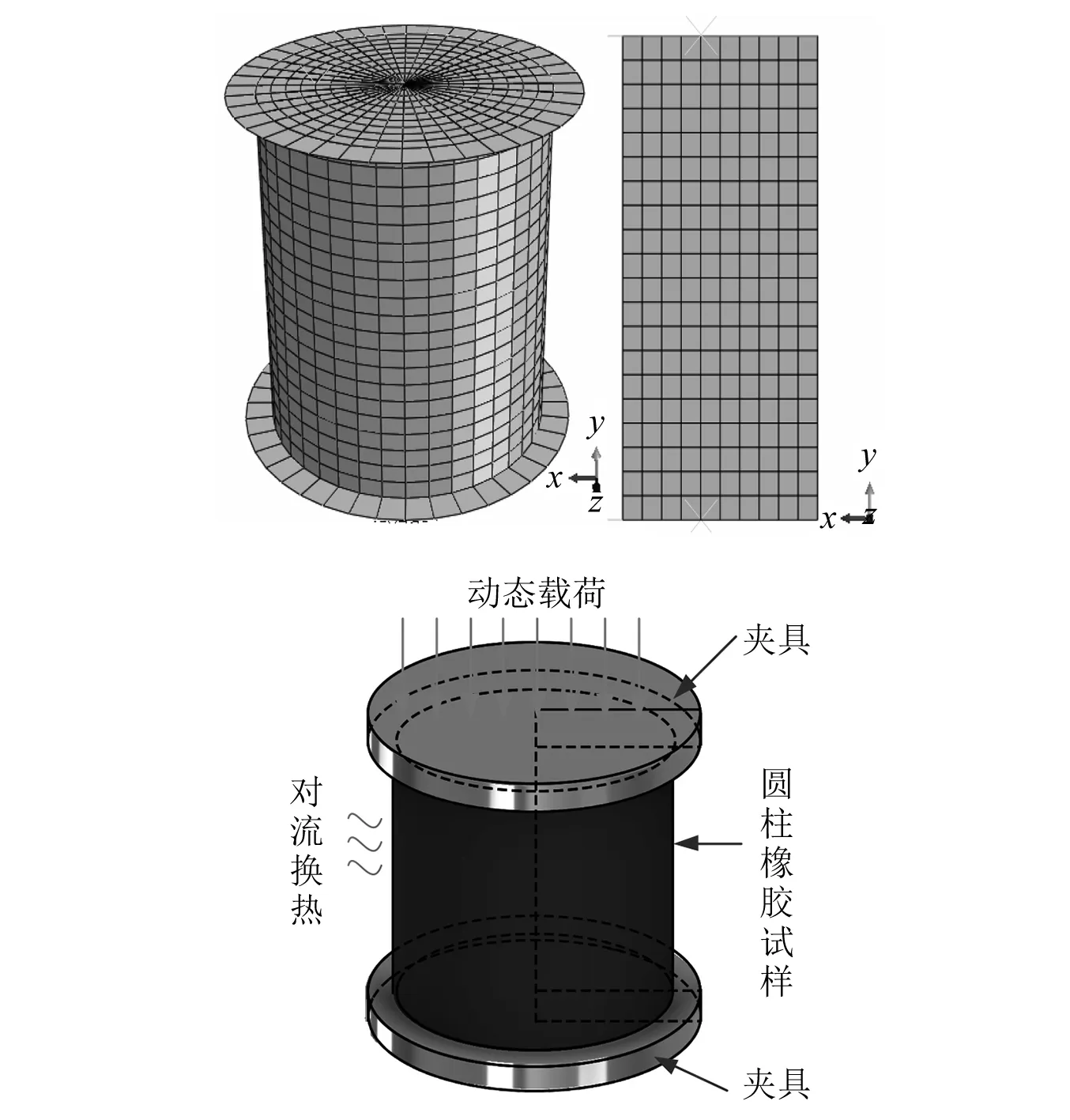
图9 圆柱试样网格划分与边界条件

表1 橡胶圆柱试样有限元模型参数

依3.1节所述流程进行Abaqus仿真分析，在圆柱试样静态预压缩20%的基础上，施加不同幅值的动态变形(1%，2%，3%，4%，5%)，载荷频率分别为10 Hz、30 Hz、50 Hz和70 Hz，计算得到不同时刻试样的温度云图。如图10为动态变形为5%，载荷频率为50 Hz时，试样不同时刻的温度场，可见仿真结果再现了黏滞损耗引起的自热升温过程，且试样内部温度高于表面温度，图11为相同加载条件下红外热像仪测得的不同时刻的试样表面温度场。将试样表面温度的仿真结果与试验测量值进行比较，如图12，可见，动态应变幅值越大，温升越明显，加载频率越高，温升越大，仿真结果与试验吻合良好，验证了本文仿真方法是有效的。图13给出了加载频率为50 Hz，动态应变幅值为5%时，圆柱试样中心温度与表面温度的仿真计算结果，表面的平衡温度为41.03℃，而中心的平衡温度为49.45℃，可见试样中心温度明显高于表面温度。

图10 f=50 Hz，ε0=-0.2，Δ=0.05条件下橡胶圆柱试样内部不同时刻的温度云图

图11 橡胶圆柱试样动态压缩过程的表面热像图

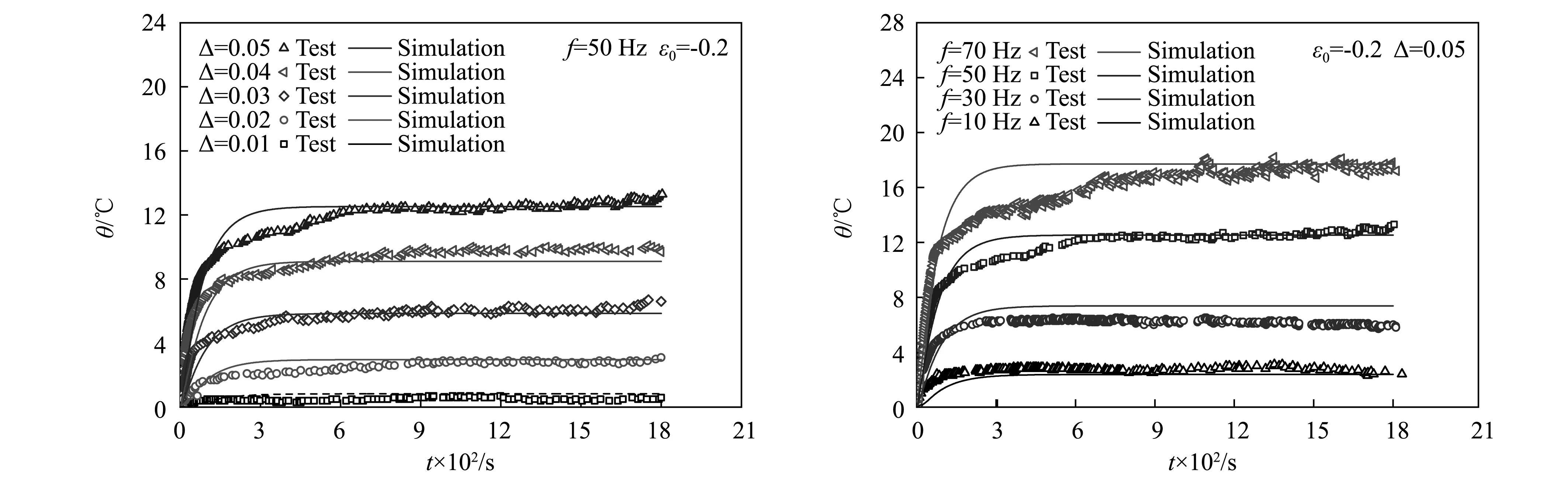
图12 橡胶圆柱试样动态压缩过程的黏滞温升：仿真计算与试验结果比较

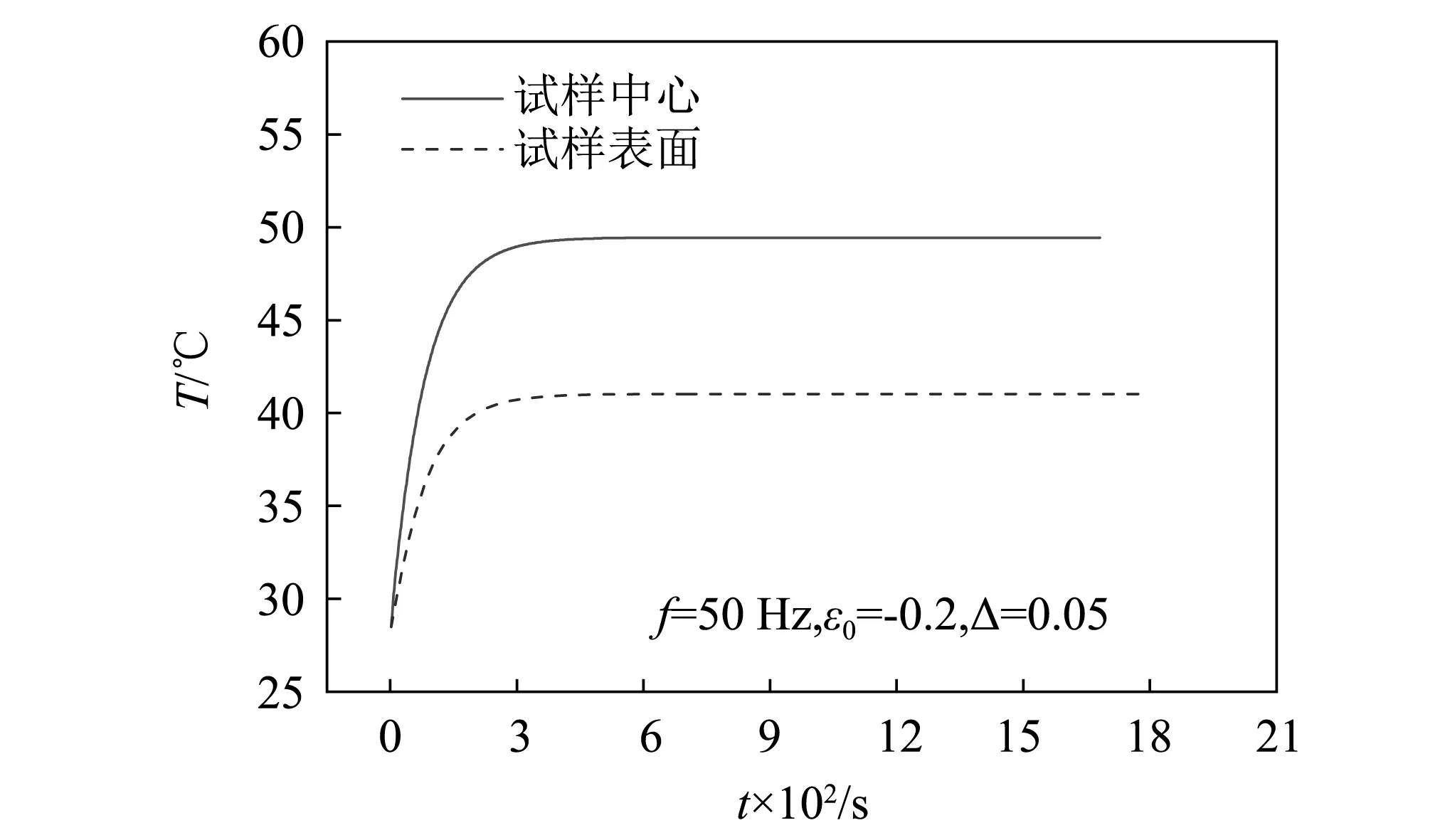
图13 圆柱试样中心与表面的温度-时间曲线(T0=28.5℃)

3.4 橡胶减振弹性元件黏滞生热仿真分析

通过圆柱试样的仿真与实验对比，验证了黏滞温升计算方法的有效性和准确性，下面对株洲时代新材料科技股份有限公司生产的某型橡胶沙漏减振弹簧动态载荷下的黏滞生热进行仿真分析，该沙漏弹簧为动车组减振部件，实物和有限元模型如图14，其中底板和顶板材料为Q235B钢，中间部分为填充橡胶，胶料配方、混炼与硫化条件均与2.1节所述试验材料一致，仿真分析采用的材料参数见表2。仿真分析设定工况为在沙漏弹簧静态预压缩5 mm的基础上，再施加动态循环载荷，频率为50 Hz，动载位移幅值Δu分别为0.5 mm、0.75 mm、1 mm、1.25 mm和1.5 mm。在给定动载位移幅值为1 mm时，分析载荷频率对黏滞生热的影响。

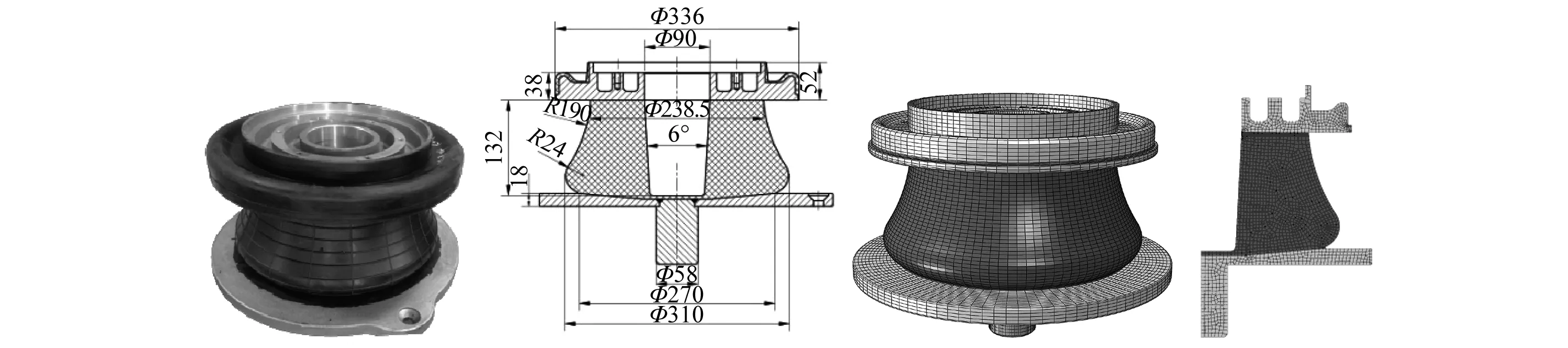
图14 橡胶沙漏减振弹簧及其有限元模型

表2 沙漏减振弹簧材料参数

如图15和图16分别显示了动态位移幅值为1 mm和0.5 mm条件下，仿真分析得到的减振弹簧橡胶部件的不同时刻温度场云图，图17为50 Hz不同动载位移幅值条件下橡胶内部中心位置和表面特定位置的温度随时间的演化曲线，图18为动载位移幅值1 mm时，不同载荷频率下的温度演化曲线。可见，各橡胶减振弹簧均有明显的温度上升，且在3 h后逐渐达到稳态。图19显示了50 Hz条件下动载位移幅值Δu对稳态温度T∞的影响，可见黏滞生热与动载幅值密切相关，稳态温度随位移幅值的增大而升高，动载幅值为0.5 mm时，表面平衡温度为31.88℃，中心平衡温度为47.57℃；当动载幅值增至1.5 mm时，表面平衡温度上升为40.47℃，中心平衡温度达到118.44℃。图20为载荷频率对稳态温度的影响，随着频率的增大，稳态温度呈线性升高。

图15 动载位移幅值1 mm下沙漏减振弹簧的温度场云图(50 Hz)

图16 动载位移幅值0.5 mm下沙漏减振弹簧的温度场云图(50 Hz)

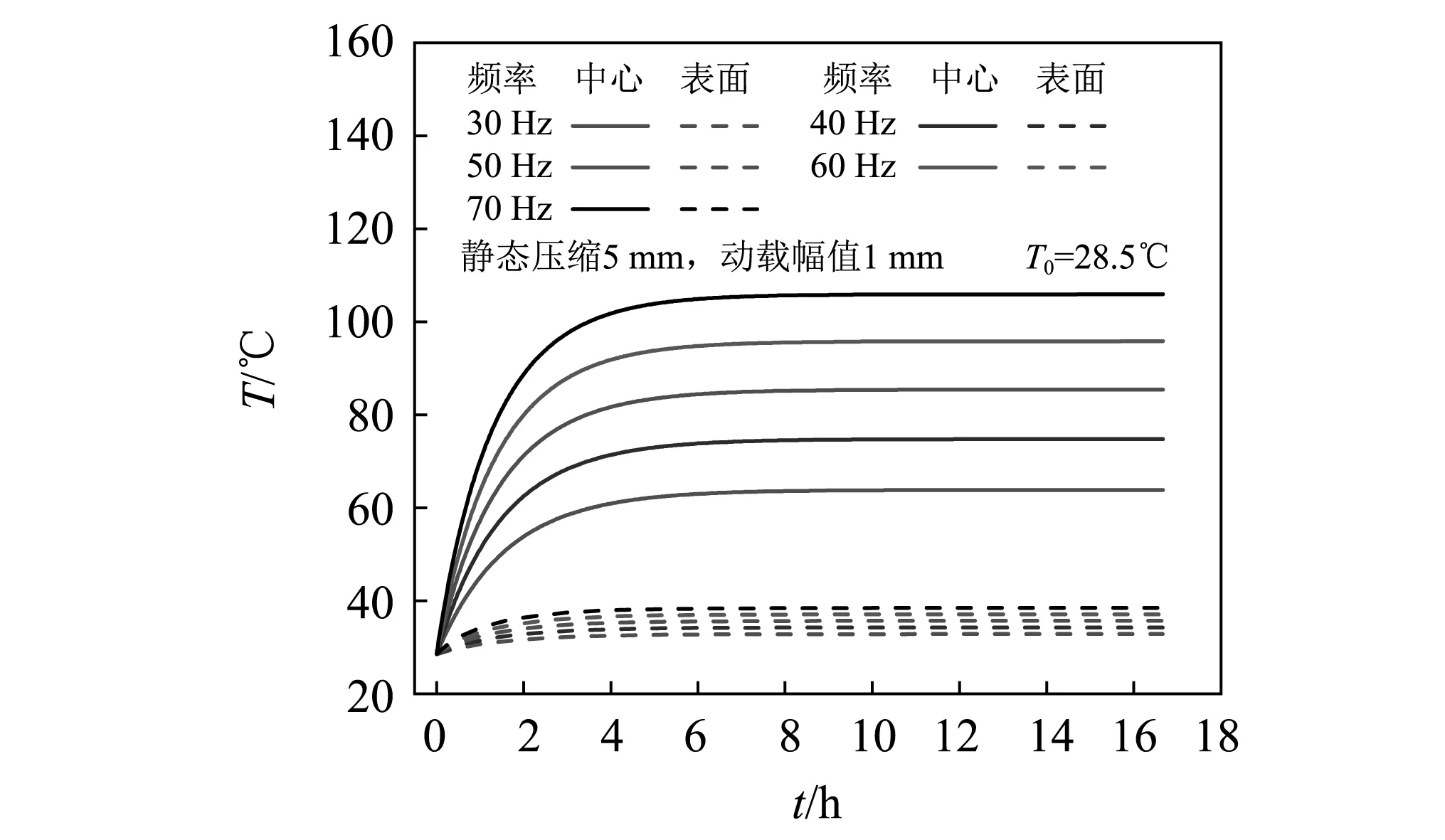
图18 动载位移幅值为1 mm时不同载荷频率下沙漏减振弹簧的温度演化曲线

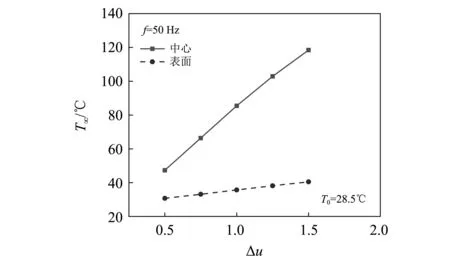
图19 沙漏减振弹簧稳态温度T∞随动载位移幅值Δu的变化(50 Hz)

图20 沙漏减振弹簧中心与外表面的稳态温度-频率曲线

4 结 论

本文考虑橡胶材料的动态黏弹性及其黏滞损耗，发展一种疲劳黏滞生热的有限元仿真方法，采用修正的Kraus模型，定量描述了橡胶材料动态损耗模量的温度、载荷频率以及应变幅值相关性，其中温度相关性满足垂直移位关系，移位因子可通过指数函数表示。仿真分析考虑了动态黏弹损耗引起黏滞生热，温度变化又反过来改变损耗模量的热力耦合效应，黏滞生热率由黏弹性理论确定，取决于载荷频率、应变幅值和温度。对橡胶圆柱试样动态压缩过程的生热仿真分析定量再现了试验过程，说明本文仿真方法是有效的，橡胶沙漏减振弹簧疲劳过程的热力耦合仿真分析表明，橡胶内部自热温升剧烈，且温升随载荷频率和幅值的增大而升高。