一种面向SRAM 型FPGA 的三模冗余分区自修复方法研究*

王 鹏，刘正清，田 毅

（中国民航大学 适航学院，天津 300300）

0 引言

随着航天技术的蓬勃发展，航天系统对电子器件的性能要求越来越高。在航天电子设备的设计中，基于SRAM 的FPGA 由于其现场可编程性、维修成本低等优点，使其比专用集成电路（Application Specific Integrated Circuits，ASICs）更有优势。航天环境中的电子系统设计，不仅要满足对性能的需求，数据传输时的可靠性和电子系统的可用性也必须得到保证。暴露在高电磁辐射中，工作中的电子器件会持续受到高能粒子撞击以致辐射效应，如单粒子翻转（SEU）等[1]，由辐射引起的单粒子翻转在导致空间环境中电子系统失效的原因中占很大的比例。所以需要提高电路的抗辐射干扰能力。

三模冗余（TMR）是一种广为人知的抗干扰容错技术，可以对单粒子翻转有较好的容错效果[2]。该方法使用3个相同的逻辑块同步执行相同的任务，每个逻辑块相应的输出通过表决器比较并进行多数表决，进而在一定时期将故障产生的影响屏蔽起来，使得发生故障的电路依旧可以在一段时间里继续工作。这种方式并未将故障解决，随着故障的持续增加，系统仍然有发生失效的可能性。所以如果使三模冗余电路具有一定的自修复能力，则可提高系统的可用性，图1 即为一个标准的TMR 结构。本文从自修复的角度对传统的三模冗余进行分区改进，并分析分区和刷新频率对系统可用性带来的影响。

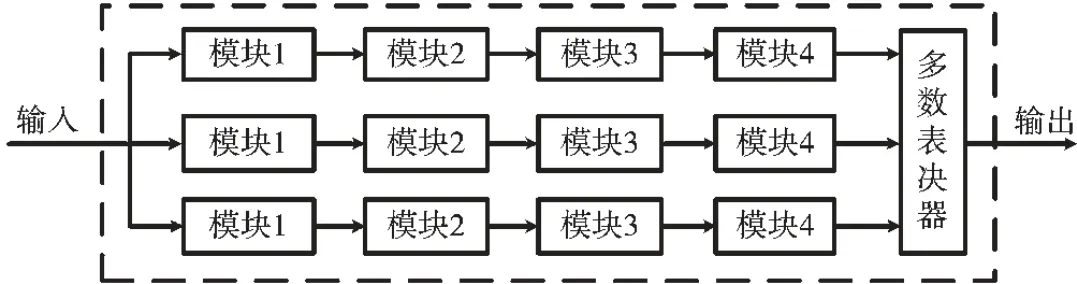
图1 标准TMR 结构

1 TMR 分区

在基于SRAM 型FPGA 中，用户的组合和时序逻辑都是由定制逻辑存储单元实现的，也就是SRAM 单元。当翻转发生在FPGA 中的综合组合逻辑中时，它实际对应于LUT 单元或在控制布线单元的一个位翻转。在LUT存储单元翻转意味着组合逻辑发生了改变。影响只能在配置位流的下一次载入时才会被修正。这种翻转的效果与LUT 定义的组合逻辑的固定故障（1 或0）相关。这意味着，除非使用一些检测技术，在FPGA 的组合逻辑发生的翻转将被存储单元锁存。布线的翻转可以连接或断开阵列中线的连接，可能产生有永久的影响，其效果可以映射到FPGA 实现的组合逻辑的一个开路或短路回路。故障也将在配置位流的下一次加载被修正。

需要注意的是使用TMR 本身是不够的，为了避免FPGA 的错误，还要求比特流强制性不断地进行重新加载，这就是所谓的刷新过程。刷新使系统能够修复SEU导致的配置存储器的错误而不破坏其操作。在本研究中使用盲刷新（定时刷新）来进行修复SEU 的操作[3]。盲刷新的优势在于可以不用精确定位故障点，减少操作；劣势在于需要将整体目标电路配置全部刷新，如果周期设置得不合理，将大大降低目标电路的使用时间[4]。

将两种技术结合可以在容错的基础上增加自修复的能力，将单纯的容错电路转化为可以定时修复故障的容错电路，可以有效减少故障累积。

2 模型检测

模型检测是一种成熟的验证技术，用于验证有限状态的系统的正确性[5]。给定系统的模型，根据标记的状态转换和与时间逻辑相关的属性进行仿真计算，模型检查算法会遍历系统中有可能出现的所有状态以验证系统的性能。概率模型检查可以对表现出随机行为但状态有限的系统进行建模。在本文中由于需要利用系统的数据流图来进行建模，所以使用具有过渡和状态标签的连续时间马尔科夫模型来进行随机建模。

在本文中将使用PRISM 验证工具[6]来进行建模和分析，文献[7-8]中表明可以使用PRISM 验证工具进行构建马尔科夫模型。首先对分区三模冗余，使用连续时间马尔科夫链对系统进行建模。然后利用系统的数据流图，对分区数量、刷新频率等参数进行预期。最后使用PRISM 验证使用概率瞬态逻辑[9]表示的与系统可用性相关的属性。

3 模型建立及定量分析

3.1 模型建立

在本文中选择的待测电路为FIR 滤波器电路。滤波器通常用于数字通信系统中，例如信号分离、降噪等。对于从卫星到无人飞行任务中的所有航天应用，通信都是一个基本问题，所以数字滤波器在此类系统中非常重要[10]。为了说明此方法的适用性，故使用SCU 模型分析8 比特64 抽头FIR 滤波器，FIR 滤波器在有足够运算能力的前提下可以无限增加精度[11]。N 抽头FIR 滤波器的离散脉冲响应可以表示为：

其中，x[ ]、y[ ]和h[ ]分别表示输入、输出和单位脉冲响应。

每个分区中的一行模件组合定义为一个域，每个域的故障率即由所有模块的故障率和表决器的故障率加和决定。

其中，λi表示模块i 的故障率，λvoter表示表决器的故障率。

在TMR 中，虽然同一分区中每个域在物理上是独立的，但故障率相同，所以每个分区的故障率λP为：

图2 显示了一个双分区TMR 数据流图。第二分区中比第一分区多了3 个表决器，其中每个模件的故障率λm为：

图2 待测电路双分区三模冗余数据流图

在本文的实验中，λbit=5.79×10-13SEUs/bit/s 代表了30 000 英尺高度SRAM 芯片IMS1601 的SEU 概率[12-13]，Nkey表示关键比特数量，关键比特数量可以从模件的表征库（Characterization Library）查询到[14]。

基于每个域的故障率、用户定义的分区数量和刷新频率，然后构建系统的连续时间马尔科夫模型并使用PRISM 建模语言进行编码。之后使用PRISM 模型检查器验证不同的可靠性和可用性属性，根据定量分析的结果来评估系统是否符合要求。

首先从TMR 的每个分区开始建模，定义一个有N个分区的系统为：

其中，每个Pi∈P 表示一个TMR 分区。

对于单粒子翻转模型，每个模块的失效是独立的。由于配置IP（导致单粒子翻转发生）产生的故障时间呈指数分布，假定配置刷新概率也遵循指数分布，即μ=1/τ，其中τ 表示刷新间隔[15-16]。

图3 显示了一个可自动修复TMR 的马尔科夫模型。最左边的模块表示三模电路有3 个域正常运行，此时分区的失效率是3λ；中间的有两个域正常运行，失效率是2λ；最右边的只有一个域正常运行，系统失效。在这个模型中μ 代表刷新频率。

图3 一个可自动修复三模冗余马尔科夫模型

每个Pi∈P 都可以被描述为一个连续时间马尔科夫模型。定义：

图4 显示了一个双分区可自动修复的三模冗余马尔科夫模型。其中λpj和λpi分别表示两个分区的失效率。状态④，⑤，⑦，⑧表示系统可运行；状态0，①，②，③表示系统失效。系统运行情况可由下式表示：

图4 双分区三模冗余的单粒子翻转马尔科夫模型

在本文的分析中，生成了3 种马尔科夫模型，分别为无分区、双分区和四分区。模型的复杂度从无分区到四分区的总状态数和转换次数随着分区数量的增加而增加，分区会变得比较复杂，因为在单独的域中对同步的SCU 进行建模需要越来越多的转换，为了能够保持这种建模方式的可管理性，将每个分区分别作为PRISM 语言中的模块，并利用PRISM 模型检查工具进行模块的并行组合（代表TMR 分区），以生成完整的分析模型。表1为通过PRISM 建模及仿真出的模型状态统计。

表1 模型状态统计

3.2 定量分析

可用性定义为系统正常运行的时间和系统运行的时间的比率。图5 显示了无分区/双分区/四分区时系统的可用性与不同的刷新间隔之间的关系。在PRISM 中可以用R{“up_time”}=?[C ＜=T]/T，T=1 month.来做属性检测。评估时将刷新间隔定为15 min～4 h。从图5 中可以看出，当刷新间隔增加时，系统的可用性降低。然而，当刷新间隔相同时，具有更多分区的可用性有着明显的提高，对于可用性而言，分区数量对于较长的刷新间隔有着比较重要的影响。例如在刷新间隔为4.00 h 的时候，无分区的可用性在0.975 左右，双分区的可用性在0.985 左右，四分区的可用性则达到了0.99 以上。由于TMR，将面积和功耗至少增加300%，频繁的刷新将浪费掉很多系统资源。

图5 无分区/双分区/四分区的可用性对比

对于这样的情况，增加分区数量可以提供一个好的解决方案，而不是更频繁地进行刷新。例如，如果设计人员的目标是高于0.99 的可用性，并设计中没有考虑分区，那么设计人员可能会考虑用频繁的刷新来满足一些要求。这时设计人员可以采用多分区的TMR 来满足需求，从图5 中可以看到，当系统四分区时，即使刷新间隔延迟2 h 也可以满足相同的可用性。使用这种方法，设计者可以确定满足给定刷新频率的设计要求的分区数量，反之也同样可以通过分区数量来确定合适的刷新频率。

4 结论

本文针对SRAM 型FPGA 的结构特点，将电路分为若干模块，采用三模冗余和配置刷新相结合的方法对电路的性能进行优化，建立模型并用PRISM 验证工具进行检验。实验结果表明，该设计可以有效提高电路的可用性。在设计系统时，可以综合考虑电路结构、资源分配情况来合理地调整分区数量和刷新间隔，灵活组合，以使电路有更佳的性能。