基于河相关系的分汊河道整治线宽度计算研究——以长江下游东流水道为例

张玮，刘容

（河海大学港口海岸与近海工程学院，江苏 南京 210098）

0 引言

整治建筑物是改善航道条件，提高航道等级的主要工程措施，而整治线宽度的确定则是航道整治工程设计的主要内容。对于单一河道，通过布置整治建筑物，可以集中水流，冲刷航槽，提高航道尺度。但是，对于分汊河道，在通航汊道布设整治建筑物，虽然可以改善航道条件，但也可能同时增加该汊水流阻力，减少分流比，进而不利于过水断面的稳定，反过来又影响通航汊道的航道尺度。因此，开展分汊河道整治线宽度的计算研究是十分重要的。

整治线宽度是指整治水位时的河面宽度，也就是河道两侧整治线之间的宽度。目前，确定整治线宽度的方法主要有经验方法和理论计算方法。经验方法主要包括河相关系法、优良河段经验法等，理论计算方法主要包括水力学计算法、河流动力学计算法等。唐存本[1]曾提出河床断面法来确定整治线宽度，是经验方法的概括和发展，通过分析大量的实测资料，认为在冲积河流中，河床形态是水、沙相互作用，相互调整的结果。如果某种水沙条件具有适当的稳定历时，就会塑造出相应稳定的河床断面形态。若能控制住整治流量下的河宽，就可以得到所需要的航深。窦国仁[2]首先提出“整治前后输沙能力相等”的平衡输沙原理，在国内开创了使用河流动力学方法开展整治线宽度研究的先河，此后众多学者先后进行了补充和完善，较有影响的有刘建民[3]、卢汉才[4]、张沛文[5]、张幸农[6]等。

冲积河流的河床形态要素与水流、泥沙条件之间常常存在某种函数关系，通常称之为河相关系。孙志林等[7]基于分汊前后水流挟沙能力相同的假设，得到了分汊前后断面面积之比与汊道分流比的指数关系，并用实测资料进行了验证。张玮等[8]将局部最优能耗原理从单一河道拓展应用于分汊河型，推导建立了分流比与汊道过水断面面积比之间的河相关系，利用长江下游东流水道等多个分汊河段的实测资料，对公式进行了验证。在此基础上，进一步对所推导的公式进行了简化。

本文将基于平衡输沙原理和河相关系原理，提出分汊河道航道整治线宽度的计算公式和计算方法，结合长江下游东流水道航道整治工程实例，开展计算分析比较研究，并就有关问题展开讨论。

1 基于输沙平衡的计算方法

1.1 单汊河道的计算公式

输沙平衡法认为，天然河流原本已处于相对平衡状态，但浅滩段水深不足，需修建整治建筑物束窄河床，加大流速冲刷河底浅区。因河床冲淤变化很快，河床变形中的复杂变化可不予考虑。当河床冲刷变化达到预计要求设计水深后，原浅滩段的输沙能力恢复到与整治前相同，达到新的输沙平衡。

对于底沙造床的情况，可采用沙莫夫输沙率公式，由此推导求得整治线宽度计算公式如下（公式推导过程见文献[9]）：

式中：B1、B2为整治工程前后的整治线宽度；Q1、Q2为工程前后整治断面的流量；H1为工程前整治水位时的平均水深；t 为整治水位下的航道水深；η为水深改正系数，一般取0.8～0.9；y1、y2为经验指数；m 为经验系数，取值1.26、2.22、5.36。

对于单一河道来说，航道整治工程实施前后，整治断面的流量通常没有变化，因此式（1）可以改写为：

经过长期的航道整治工程实践，已经取得了丰富的经验，并在JTJ 312—2003《航道整治工程技术规范》中将整治线宽度计算公式统一表达为：

式中：k 为经验系数，可取1，在复杂情况下取0.8～0.9；y 为指数，稳定河床取1.67，以悬移质造床为主的河流取1.33，以底沙造床为主的河流取1.2～1.4。

当然，对于分汊河道，还应考虑整治前后通航汊道分流量的变化，参照式（4）可得到下式：

1.2 分汊河道的整治线宽度计算方法

对于分汊河道来说，整治线宽度的确定相对要复杂一些。整治线宽度主要用来指导整治建筑物布置，对于单一河道，整治工程实施以后流量通常不会改变。但是对于分汊河道，整治工程则可能改变通航汊道的分流量，进而影响整治线宽度的确定。因此，分汊河道整治线宽度的确定只能采取假定计算，进而校核，再行调整的反复过程，也就是：

1）首先，假定整治工程实施前后通航汊道的分流量保持不变，由此可以参照单一河道的方法，按照式（4）计算通航汊道初始整治线宽度。

2）根据计算的初始整治线宽度布置整治建筑物，由于工程实施后将调整汊道间的阻力，导致分流量改变，所以必须通过计算或试验研究等方法，确定工程后通航汊道的分流量。

3）根据工程后通航汊道分流量，按照式（5）重新计算通航汊道整治线宽度，并进行校核。如果计算结果满足精度要求，则可以停止计算；否则，应该重新选择整治线宽度或修改整治工程方案，重复步骤2）的过程，直至满足要求为止。

2 基于河相关系的计算方法

基于河相关系，也可以进行分汊河道整治线宽度计算。对于长江下游河段，文献[8]给出了分汊河道分流比与过水断面面积比之间的河相关系：

对于航道整治汊道，整治工程前的分流量Q1，对应的面积A1，整治工程后的分流量Q2，对应的面积A2，其均应满足式（6），分别代入式（6）并将其相除可得：

参考式（5），可以得到整治线宽度计算公式：

式（8）中，整治工程前的通航汊道分流量、过水断面面积是已知的，整治工程实施后，可以根据新的通航汊道分流量计算整治线宽度。

类似地，在计算分汊河道整治线宽度时，也可以首先假定通航汊道分流量工程前后保持不变，按照式（8）计算出初始整治线宽度，据此布置整治建筑物；然后，研究整治工程实施以后通航汊道分流量的变化，并按照式（8）重新计算整治线宽度，如果计算结果满足精度要求，则停止计算；否则重复上述过程，直至满足要求为止。

3 分汊河道整治线宽度计算分析比较

3.1 工程实例

东流水道位于长江下游九江市—安庆市之间，上起华阳河口，下至吉阳矶，全长约31 km，属顺直分汊河道。按平面形态可分为3 段：进口顺直放宽段、分汊段和出口微弯段。东流水道先后进行过两期航道整治工程。一期工程于2004 年2月开始施工，2010 年3 月竣工，主要包括老虎滩守护工程、左岸丁坝群工程及玉带洲头鱼骨坝工程，见图1。二期工程于2012 年11 月开工建设，2014 年4 月主体工程基本完成。主要由老虎滩头部鱼骨坝工程、老虎滩左缘护滩带加固工程、天玉串沟守护工程、七里湖护岸工程及老虎岗护岸加固工程4 部分组成，见图1。在进行二期航道整治工程设计时，东流水道设计通航水位取3.53 m（黄海基面），整治水位取设计水位以上3.0 m。

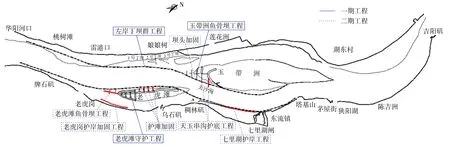
图1 东流水道河势图Fig.1 River regime of the Dongliu waterway

3.2 输沙平衡计算方法

在计算时，选取系数k=0.8，指数y=1.33，水深改正系数η=0.9，系数m=2.22，则y1=1.24。根据当时的水下地形资料[10]，求出老虎滩北槽（左槽）整治水位时的平均河宽B1=2 200 m，平均水深H1=6.0 m，航道水深t=7.5 m。由此，可进行整治线宽度计算：

1）首先，假定工程实施以后，老虎滩北槽分流量不变，利用式（4）计算初始整治线宽度B2=1 504.8 m，取为1 500 m。

2） 按照初始整治线宽度，布置整治建筑物等，通过数值计算和物模试验，研究工程实施前后北槽分流量（分流比）变化，具体结果见表1 和表2。

表1 整治工程实施前后不同流量级分流比变化表（数模）Table 1 Comparison table of the bifurcating discharge ratio in different flow levels before and after the implementation of the regulation project(mathematical model) %

表2 推荐方案系列年试验各年末枯水流量（Q=13 200 m3/s）下分流比Table 2 The bifurcating discharge ratio under low discharge（Q=13 200 m3/s）of the end of each year through annual test of recommended schemes %

3）数值计算结果表明：工程实施以后，整治水位下老虎滩北槽的分流比有所增加，由工程前62.0%增加到工程后的70.6%，增幅为13.87%，此时，可按照式（5）重新计算整治线宽度，得到整治工程实施后，整治线宽度B2=1 767.8 m，比初始整治线宽度1 504.8 m 增加了263 m，增幅为17.47%。由此可见，随着分流比的增加，对应的整治线宽度也相应放宽。

4）系列年物理模型试验结果表明：整治工程实施以后，历年枯水期老虎滩北槽的分流比略有增加，由60.0%增加到61.9%～62.9%，分流量增幅3.17%～4.83%，利用式（5）重新计算整治线宽度为1 554.1～1 595.5 m，与初始整治线宽度相比均有所增加，分别增加了49.3～90.7 m（3.28%～6.03%）。

5） 在研究工程实施后通航汊道分流量变化时，数学模型与物理模型的结果有一定的差异，特别是如果数学模型不考虑河床调整的情况下两者差异就更大，此时动床物理模型的试验结果应该更符合实际情况。

6）根据动床物理模型试验结果，东流水道航道整治工程实施以后，通航汊道的流量略有增加，重新计算的整治线宽度也略宽于初始值，考虑到两者相差不多，此时若仍然选用初始整治线宽度的话，总体上是可以接受且偏于安全的。

3.3 河相关系计算方法

在利用式（8）进行计算时，选取折减系数k=0.77，系数n = 0.80，由此可得指数 α = 0.953，水深改正系数η = 0.9。同样，老虎滩北槽（左槽）整治水位时的平均河宽B1=2 200 m，平均水深H1=6.0 m，航道水深t=7.5 m。由此，可进行整治线宽度计算：

1）首先，假定工程实施以后，老虎滩北槽分流量不变，由此利用式（8）计算初始整治线宽度B2=1 505.8 m，同样取为1 500 m。

2）根据数值模拟计算的分流比结果，利用式（8）重新计算整治线宽度，得到整治工程实施后，整治水位时B2=1 704.2 m，比输沙平衡法的计算结果小63.6 m，相对误差-3.6%。

3） 根据系列年物理模型试验结果，利用式（8）重新计算整治线宽度，当老虎滩北槽分流比增加到61.9%～62.9%时，对应的整治线宽度为1 551.2～1 575.1 m，较初始整治线宽度增加了45.4～69.3 m（3.02%～4.60%）；与输沙平衡法相比，两者结果相差-2.9～-20.4 m（-0.19%～-1.36%）。可以说两者的计算精度基本相当。

4 进一步分析讨论

利用东流水道的实例，说明了输沙平衡法和河相关系法都可以用来计算分汊河道整治线宽度。为了便于进一步讨论，假设整治工程实施后，通航汊道的分流量有所变化，其中，Q2/Q1=1.0 代表整治前后通航汊道分流量没有变化，据此计算的结果就是初始整治线宽度，而Q2/Q1等于0.95 和1.05，则分别代表工程实施后通航汊道分流量减少5.0%和增加5.0%，计算结果见表3。

表3 分流比变化时整治线宽度计算结果Table 3 Calculation results of regulation width with the change of bifurcating discharge ratio

表3 计算结果表明：

1）整治工程实施以后，随着通航汊道分流量的增加，整治线宽度相应的也有所拓宽，可利用输沙平衡法或者河相关系法进行计算，且两者结果相近。当分流量增加20%时，两者相对误差在5.0%以内；当分流量增加10%时，两者相差不足2.6%。

2）整治工程实施以后，随着通航汊道分流量的减少，整治线宽度相应的也有所束窄，同样可利用输沙平衡法或者河相关系法进行计算，且两者结果相近。当分流量减少20%时，两者相对误差在6.7%以内；当分流量减少10%时，两者误差不足3.1%。

3）表3 中最后一列为使用河相关系法计算整治线宽度时，根据工程实施后通航汊道分流量变化情况，初始整治线宽度（Q2/Q1=1 对应的宽度）改变率的计算结果。结果表明：整治线初始宽度的改变率与分流量改变率基本呈线性关系，例如，Q2/Q1=0.95 也就是减少5.0%时，整治线宽度相对于初始值也减少4.8%；而当Q2/Q1=1.05 也就是增加5.0%时，整治线宽度相对于初始值也增加4.8%。由此可见，整治线宽度相对于初始值的改变率（绝对值）略小于工程后通航汊道流量的改变率。

5 主要结论

1） 整治线是指导整治建筑物布置的主要依据，对于单一河道，整治工程实施后一般不会改变流量，但是对于分汊河道，整治以后通航汊道的分流量将会有所改变，反过来影响整治线宽度的确定。

2）在进行分汊河道整治线宽度计算时，可以先将其视为单一河道计算初始整治线宽度，布置整治建筑物；然后，分析研究整治工程实施后通航汊道分流量的变化情况，重新计算，如果精度满足要求，则停止计算；否则，需要调整初始宽度，重复以上过程。

3）基于平原冲积河流河相关系原理，提出分汊河道整治线宽度计算公式和计算方法，并利用长江下游东流水道实测资料进行了计算验证，结果满意。

4）在进行分汊河道整治线宽度计算时，既可以使用平衡输沙法，也可以使用河相关系法，两者结果差异较少，通常可以两种方法并用，以便相互比较。

5）东流水道航道整治工程实施以后，通航汊道的分流量略有增加，重新计算的整治线宽度相较于初始值也略有放宽，考虑到两者相差不多，若此时仍然选用初始整治线宽度不变的话，总体上是可以接受且偏于安全的。