采用LCL滤波器的无电压传感器三相并网逆变器技术

曹以龙, 余小婵

(上海电力大学 电子与信息工程学院, 上海 200090)

当今社会电子电源的应用日益广泛,日常生活中各种各样的产品无不以电源为依托,使电源技术也逐步成熟壮大起来。以电力电子为核心的电子电源已成为当今社会不可或缺的一部分。针对逆变电源设计,三相并网逆变器的主要研究控制方法有基于电网电压定向控制(Voltage Oriented Control,VOC)和虚拟磁链定向控制(Virtual Flux Oriented Control,VFOC),但通常都需要采样电网电压、电网电流以及直流输入电压。电压传感器是并网逆变器的主要测量元件,但众多的传感器也带来了成本高、复杂性强、可靠性差等问题。因此,许多研究者对取消传感器策略进行了相关研究。文献[1]采用了传统三相LCL逆变器控制策略,基于电压外环与电容电流内环以消除谐振尖峰所引起的系统振荡。文献[2]应用一种单相无电网电压传感器的模型,采用了有功功率和无功功率的电网电压估计方法,但其结构过于简单,模型相对比较单一。文献[3]利用电流信号的微分量来估算电网电压的空间角度,但该方法很容易引入和放大噪声干扰。文献[4]和文献[5]采用各种方式减少传感器,但不能实现很好的电流保护,工业应用不多。文献[6]提出取消电网电压传感器的策略,减小了并网技术的研究成本。在进行深入研究过程中,发现针对三相LCL滤波器,存在滤波电容的Y型接法和Δ型接法两种接线方式。基于上述研究,本文提出了一种改进型无电压传感器的三相LCL并网逆变器的控制策略。

1 三相LCL滤波器滤波电容接线方式

1.1 Y型接法

LCL滤波器滤波电容Y型接法的单相等效电路如图1所示。LCL滤波电容的Y型接线方式如图1中虚线框所示,其三相状态空间模型是在单相模型基础上推导而得的[7]。

图1 LCL 滤波器滤波电容Y型接法的单相等效电路

由基尔霍夫电路定律推导可知,单相LCL滤波器的数学模型为

(1)

文献[8]提出各相之间不存在交叉耦合,所有相的方程均可等同,所以三相LCL滤波器数学模型可用矩阵形式表示为

(2)

1.2 Δ型接法

三相LCL滤波器滤波电容Δ型接法的等效电路如图2所示[9]。

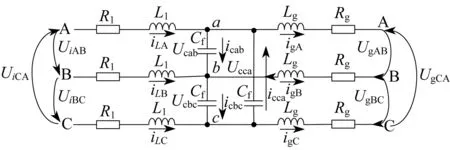
图2 三相LCL滤波器滤波电容Δ型接法的等效电路

其数学模型推导可知,滤波电容器的电压平衡方程为

Ucab+Ucbc+Ucca=0

(3)

流过电容器AB两相的电流方程可表示为

(4)

其中,iLAB=iLA-iLB,igAB=igA-igB。

由基尔霍夫电压定律可推得,桥臂侧电压平衡方程为

(5)

同理可推导出电网侧电压平衡方程为

(6)

为便于进行矩阵形式表达,可以统一表示为

(7)

其中,UC=[UcabUcbcUcca]T,iL=[iLABiLBCiLCA]T,ig=[igABigBCigCA]T,Ui=[UiABUiBCUiCA]T,Ug=[UgABUgBCUgCA]T。

因此,连续状态空间模型可以表示为

(8)

(9)

2 三相LCL滤波器的频率响应与参数设计

2.1 三相LCL滤波器频率响应

分析由滤波器所建立的数学模型可知,LCL滤波器为一个三阶系统,存在谐振尖峰容易引起系统振荡问题[9]。为解决这一问题,采用引入滤波器阻尼电阻来保证系统的稳定裕度,提高控制器的稳定性能。无阻尼状态下的LCL滤波器的传递函数为

(10)

引入阻尼电阻Rf的LCL滤波器的传递函数为

HdLCL(s)=

(11)

在引入滤波电容阻尼电阻后,取系统控制的开关频率为10 kHz,绘制出不加阻尼与加入阻尼电阻后的Bode图。对比情况如图3所示。由图3可以看出,LCL滤波器在无阻尼状态下谐振频率点处呈现一个谐振尖峰。而在引入滤波电容电流内环情况下,引入阻尼电阻可以大大削减谐振峰值,使得系统能够安全稳定地运行,从而能够很好地避免共振问题[10]。

图3 LCL 滤波器有无阻尼控制的Bode图

2.2 三相优化LCL滤波器算法的参数设计

三相优化LCL滤波器的设计需要运用到系统模型的基值参数,分别为逆变器侧的线电压有效值ULL,逆变器输出的相电压有效值Uph,额定功率Pn,直流侧电压Udc,电网频率fg,开关频率fsw,谐振频率fres。

基极阻抗和基极电容分别为

(12)

(13)

式中:ωg——电网角频率。

滤波电容的设计需考虑到电网所能允许的最大功率因数变化为5%,其滤波电容Cf=xCb,x=0.05,故Cf=0.05Cb。三相逆变器输出端的最大电流纹波可表示为

(14)

式中:Tsw——开关周期,Tsw=1/fsw;

m——调制深度。

可以观察到在m=0.5时,最大纹波电流达到峰值。此时峰值表达式为

(15)

额定电流的10%定义为最大纹波电流[11],即

ΔIL max=0.1Imax

(16)

额定电流的计算表达式为

(17)

由此,可以推导出逆变器侧电感为

(18)

LCL滤波器设计的主要参数目标是将预期10%电流纹波限制在其自身值的20%,使得产生的纹波值为输出电流的2%[12]。逆变器谐波电流ig(h)与注入电网的一次谐波电流iL(h)之间的关系表达式为

(19)

其中,ωsw为开关角频率,r=Lg/L1。

所以,可以推算出电网侧电感Lg为

(20)

为避免谐振频率出现在低频段或高频段,需满足

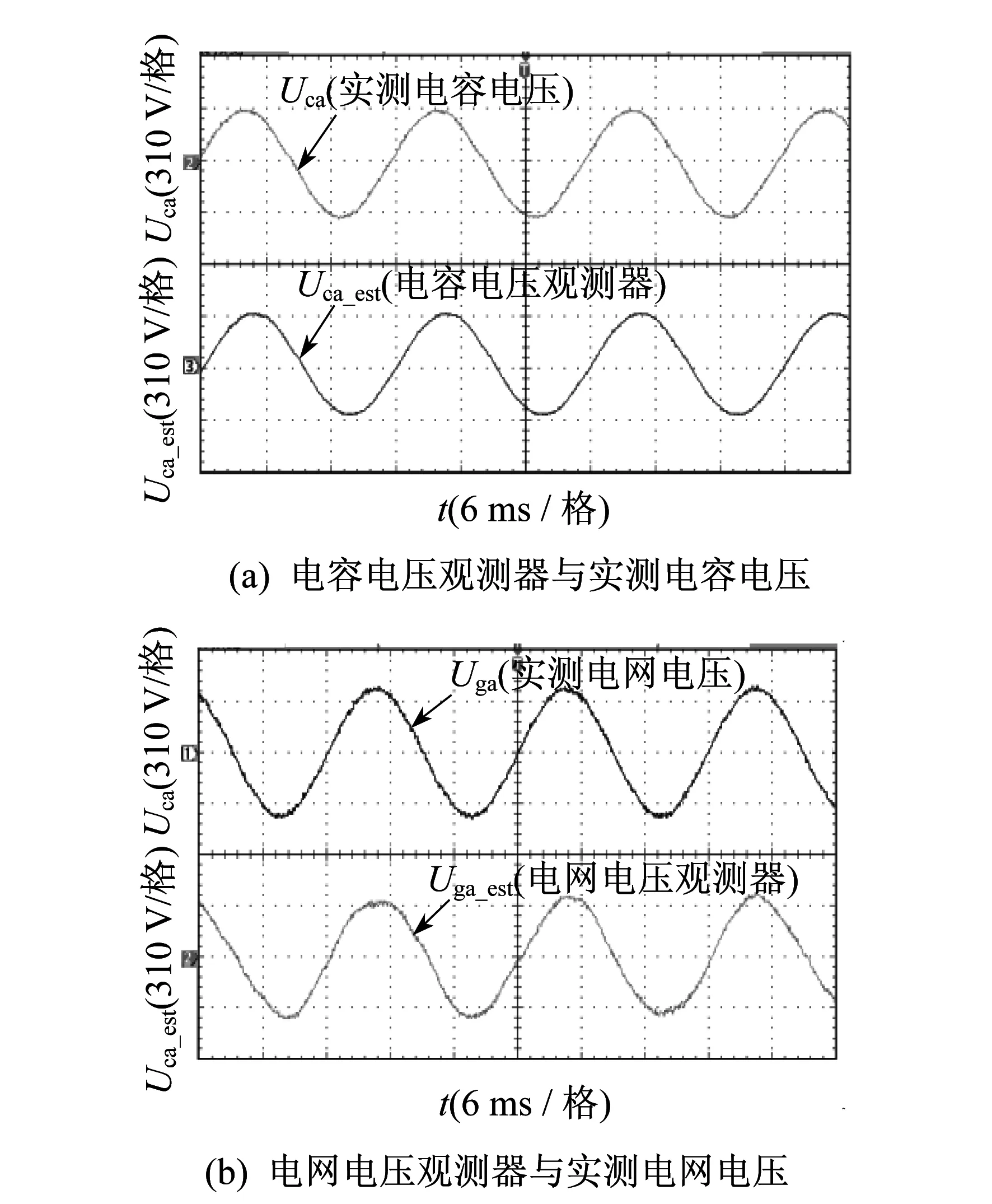
10fg

(21)

因此,可计算出谐振角频率为

(22)

最后计算出阻尼电阻Rf为

(23)

由上文所提出的LCL滤波器的参数设计,可得到:L1=2.263 mH,Lg=0.036 7 mH,Cf=15 μF,LCL谐振频率fres=6 174 Hz。

3 dq坐标系下PQ间接电流控制

3.1 准开环恒功率控制技术

在并网运行模式下,采用PQ控制方式,间接对并网逆变器输出的有功和无功功率进行控制,无电压传感器估计算法求解得到并网电压,在abc三相静止坐标下估计并网电压的三相基波电压为U。Um为相电压幅值,其表达式为

(24)

经park变换后,在dq旋转坐标系下的转换为

Tabc/dq=

(25)

再进行dq变换可得

(26)

由式(26)能够得到,三相静止坐标系下,三相并网电压是存在耦合状态的,经过dq旋转坐标系下d轴和q轴分量Ud,Uq是解耦的,且Ud为一个常量,Uq=0[13]。

对并网电流ig在dq旋转坐标系下分解可得d轴和q轴分量id,iq,此时的瞬时有功与无功功率为

(27)

在准开环恒功率控制下,在给定单位有功功率Pref与无功功率Qref的前提下,由式(26)和式(27)可推得,并网输出的参考电流为

(28)

3.2 无并网电压传感器的电流控制技术

准开环PQ控制实质是对并网电流进行间接控制,对参考电流iref的追踪间接控制了有功与无功的跟踪控制,其中有功电流id决定了有功功率P的大小,无功电流iq决定了无功功率Q的大小。其中电压估计系统是经由SOGI-QSG(基于二阶广义积分器的正交信号发生器)输出两个相互正交的分量,应用其对系统进行进一步的数学模型分析,估算出滤波器电容电压与电网电压。其控制系统结构框图如图4所示。

图4中,控制系统结合了无电压传感器的估计算法,以及PQ控制的间接并网电流控制方法,后续通过该系统仿真与实验验证了本文所提控制策略的有效性。

图4 三相电压源逆变器(VSI)无电压传感器PQ控制系统框图

4 三相并网逆变器的实验分析

数字控制器采用TI公司的浮点型DSP芯片(TMS320F28069),实际硬件电路如图5所示,其中包括所需的采样电路、三相桥臂控制电路以及其他硬件电路电子器件。系统主电路参数如表1所示。

图5 实际硬件电路

电容电压、电网电压观测器的电压波形与实际电路所测得的电压波形进行比较,结果如图6所示。由图6可以看出:观测器输出电容电压波形基本为正弦,且与实际测得电容电压波形相近,验证了本文所提方法的可行性;电网电压观测器输出电压波形与实测波形在相位上存在微小的偏移,这是由于数字控制器存在控制延时,但对实际控制影响微弱。由此验证了观测器结果的可行性。

图6 观测器电压波形与实测比较

图7为a相电网电压和经锁相环PLL估算出的电网空间角度的实验波形。由图7可知,通过SOGI-QSG电压观测器策略实现了电网空间角度的估算,具有很好的线性度。

图7 电网电压与锁相环角度波形

图8为a相电网电压与a相电网电流波形图。由图8可知,此时电网与电压同相位,电网侧电流总谐波失真(THD)保证低于5%,满足并网电流要求,使得并网逆变器能够稳定地运行,实验结果表明了所提策略的可行性。

图8 a相的电网电压和电网电流波形

5 结 论

(1) 利用电压观测器,可以广泛应用于各种场合。在电压传感器有磨损以及测量不准确时可以启用的备用算法。采用较少的电压传感器节约了成本和系统空间,增强了系统可靠性。

(2) 采用了dq坐标系下PQ间接电流控制电流控制算法,对参考电流的追踪间接控制了有功与无功功率的跟踪控制,实时性能好。

(3) 本文通过系统的数学模型分析,详细阐述了有关滤波电容的Y型接法和Δ型接法两种接线方式的分类设计和研究,为后续的理论研究提供了有力的论证基础。