基于响应面方法的H级燃机基础动力性能研究

刘森林，王忠，陈其春，周光炳，王晓，孙镝

（中国电力工程顾问集团西南电力设计院有限公司，成都610021）

“十四五”期间能源和生态环境规划等将提出碳达峰和碳中和的具体路径，从而推动天然气消费需求持续增长。天然气发电投资成本低、运行灵活，其在能源转型中的桥梁作用和在电源中的支撑作用长期内不会改变。H 级燃机是目前世界上最高效、节能、环保的大容量燃气轮机，在国际燃气轮机市场中，主要有美国GE 公司的9HA.01 型燃机、德国SIMENS 公司的SGT5-8000H 型燃机、日本三菱日立公司的M701J型燃机和意大利的安萨尔多公司的GT36 型燃机［1-2］。目前，国内首台采用H 级燃气－蒸汽联合循环机组的项目——华电广州增城燃气冷热电三联供项目，于2020 年6 月14 日其1 号机组顺利通过168 小时满负荷试运行，该项目采用的两台燃机为目前世界最先进、净效率最高的西门子SGT5-8000H 级燃气轮机发电机组，在节约能源、发展绿色经济、降低企业用能成本等方面发挥巨大作用。

H 级燃机基础作为一种新的大型特种设备动力基础，其具备优良的动力性能是燃机平稳运行的重要保证。H 级燃机基础动力性能受到质量、刚度和阻尼等因素的影响［3-4］。在设计中由于其动力性能的复杂性，往往需凭取工程经验和试算进行设计，具有一定的盲目性，并难以较清晰了解H 级燃机基础的动力性能走向。针对H 级燃机基础的动力性能，选取基础厚度、混凝土弹性模量、动扰力和阻尼比作为影响H 级燃气轮机的关键影响因素，以振动控制点最大控制幅值作为动力性能指标，通过有限元ANSYS 参数化建模建立H 级燃机基础不同基础厚度、混凝土弹性模量、动扰力和阻尼比的大量三维模型，采用谐响应分析获得不同参数模型下的最大控制振幅，建立H 级燃机基础最大控制幅值与基础厚度、混凝土弹性模量、动扰力和阻尼比之间的关系，获得对H 级燃机基础全面清晰的动力性能特征［5-6］。

1 H级燃机基础参数

1.1 H级燃机基础布置

国内首台西门子SGT5-8000H级重型燃气轮机，燃气轮机额定转速为3 000 rpm，发电机额定转速为3 000 rpm。燃机基础形式为大块式桩基基础，根据厂家提供的H 级燃机基础外形资料，其上设置设备支墩需满足燃机布置要求，设其基础厚度为TH，可确定发电机区基础为17.45 m×7.2 m×TH，燃气轮机区域基础为23.69 m×8.7 m×TH，基础下共采用44根∅800 mm 旋挖成孔灌注桩。燃机基础平面和剖面布置图如图1所示。

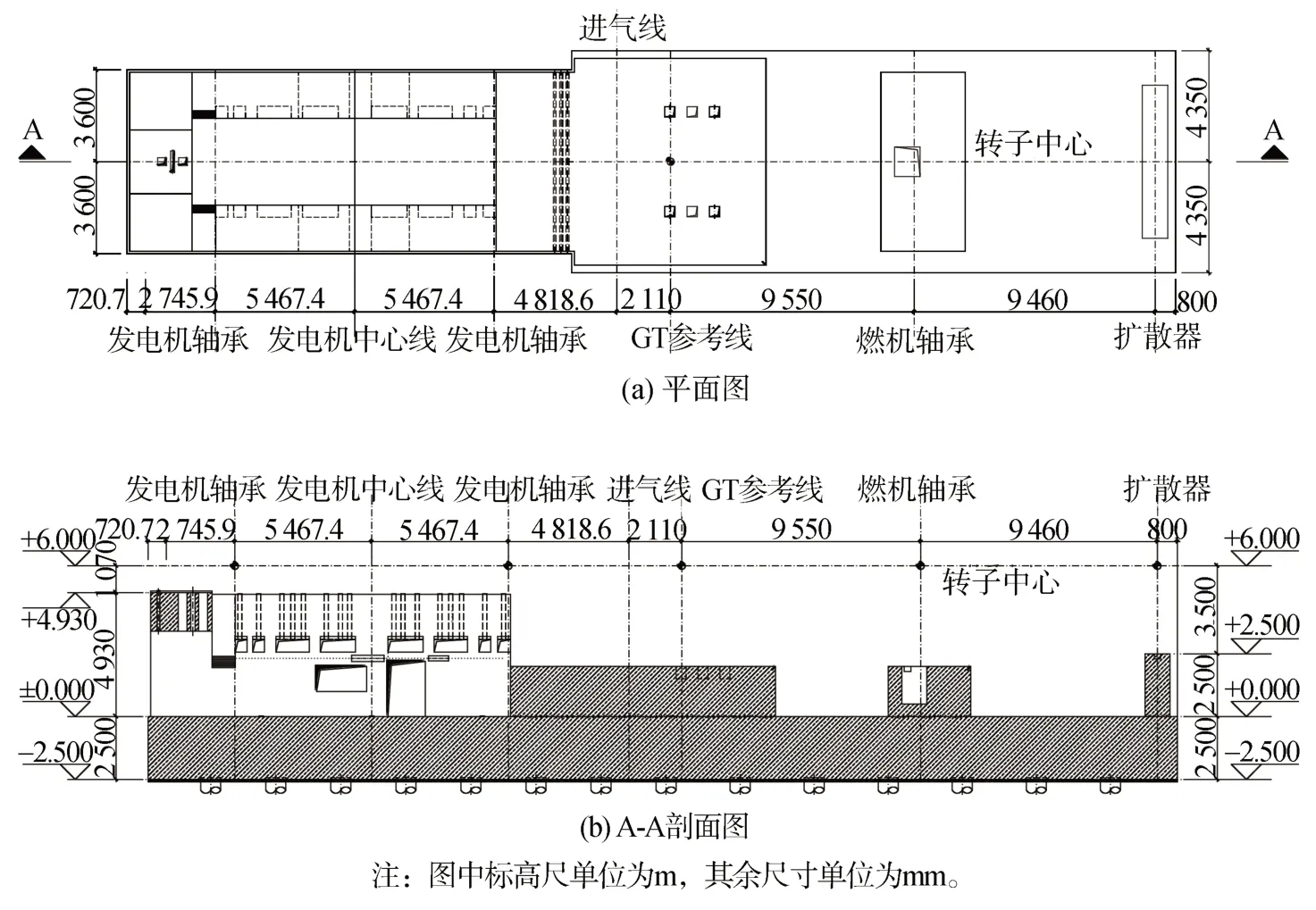
图1 燃机基础平面和剖面布置图Fig.1 Gas turbine foundation plane and section layout

1.2 振动分析方法与控制标准

H 级燃机基础在正常运行阶段燃机基础处于稳态受迫振动［7-8］。采用ANSYS 中的谐响应分析方法进行求解，谐响应分析用于确定线性结构在承受随时间按正弦规律变化的载荷时的稳态响应，分析过程中只计算结构的稳态受迫振动，不考虑激振开始时的瞬态振动。假设一单自由度弹簧振子系统承受谐激励荷载如图2所示。

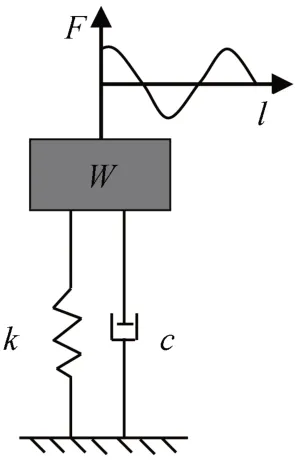
图2 单自由度弹簧振子系统Fig.2 Single-degree-of-freedom spring vibration system

此系统的动力方程为：

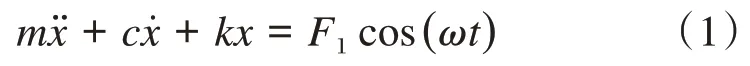
该方程的解分为两部分，一部分为齐次方程的解，即为阻尼系统的自由振动响应，自由振动响应随时间衰减直至最后消失。另一部分是特解，即为强迫振动响应，不会随时间衰减。这里进行稳态响应求解，由于燃机基础的激振力为简谐力，可以证明燃机基础的稳态响应也是简谐的，并且与激振力有同样的频率。

式中：s为振动位移响应的幅值（m）；ϕ为振动位移响应的相位（rad）。

振动位移响应幅值s、振动速度响应幅值v和振动加速度响应幅值a三者之间存在的关系为：

对于燃机基础的动力振动控制标准，国标标准ISO 20816中指出，应以轴承壳体或轴承座振动速度为基础的评价标准。对于3 000 rpm燃气轮机，新交付使用机器的振动速度均方根不应大于4.5 mm/s；对于3 000 rpm 发电机，新交付使用机器的振动速度均方根不应大于3.8 mm/s。同时，燃机厂家要求燃机基础的振动速度均方根不应大于3.8 mm/s，即对应的振动位移峰值不应大于17.1 μm。

1.3 动扰力计算

燃机在运行过程中，由于转子不平衡便在旋转机械中产生不平衡力。燃机基础动力分析时，可按转子的动平衡等级确定动扰力。该燃机基础转子动平衡等级为G2.5，阻尼比取2%，燃气轮机和发电机的动扰力根据ISO 1940/1规范按如下公式计算：

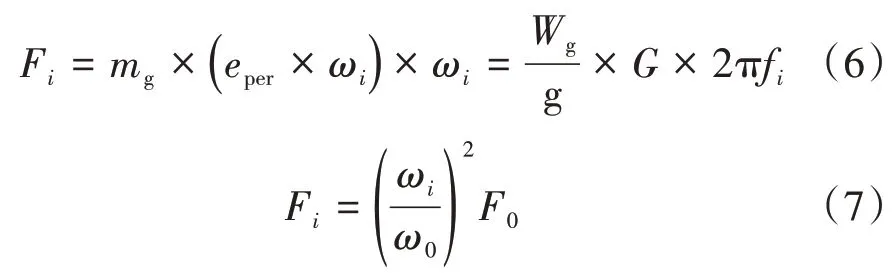
式中：Fi为任意频率的扰力（N）；mg为转子质量（kg）；eper为转子质量偏心距（μm）；ωi为任意圆频率（rad/s）；G为转子动平衡等级（mm/s）；F0为燃机额定转速动扰力（N）；ω0为燃机额定转速的圆频率（rad/s）。

将燃机的转子质量和振动频率带入上式计算得到各振动频率时横向和竖向的动扰力，燃机基础纵向的动扰力一般可取为横向或竖向动扰力的0.5倍。由于计算时需要计算额定运行频率10%范围内振动响应，这里给出当振动频率为45 Hz、50 Hz和55 Hz时，发电机和燃气轮机的竖向和横向的动扰力如表1所示。

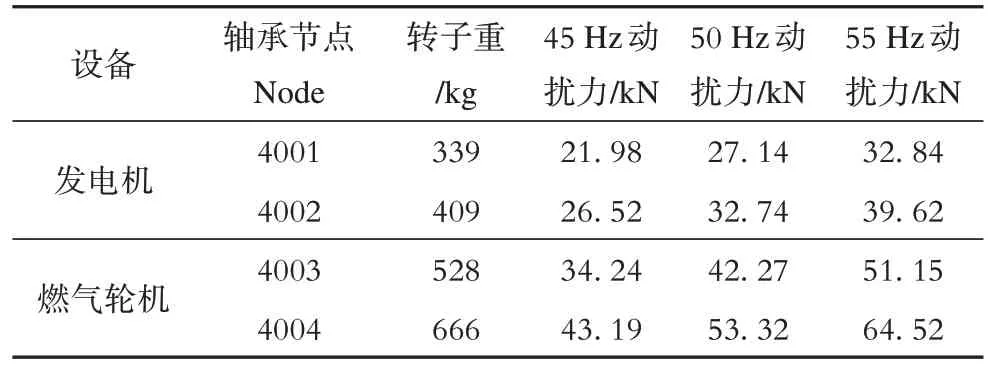
表1 发电机和燃气轮机的动扰力表Tab.1 Unbanlance force table of generator and gas turbine

2 有限元多模型建立

2.1 模型可变参数选取

H 级燃机基础动力性能由动力方程可知跟质量、刚度和阻尼三者有关系。质量一般包含机械设备质量和基础自重质量等，设备质量由燃机设备决定，由燃机厂家提供，为满足燃机设备的使用条件，燃机厂家一般会给出燃机基础顶面的支墩布置情况，燃机基础作为动力设备基础，一般需与周边基础脱开，因此，燃机基础的长宽以及顶面的布置情况一般较为固定。燃机基础的厚度变化影响着燃机基础的质量和截面刚度［9］。因此，将燃机基础厚度作为影响燃机基础的动力性能的主要可变参数。同时，混凝土材料在设计中也是可以选择的，不同标号的混凝土具有不同的弹性模量，影响着燃机基础的刚度和动力性能。因此，将混凝土弹性模量作为这里分析的另一可变参数［10］。

燃机基础的厚度通常为2~3 m，这里略微放大分析范围选取燃机基础的厚度变化范围为1.5~3.5 m，计算模型的厚度变化增量为0.1 m，共21个厚度值；燃机基础的混凝土选取C20~C50，其弹性模量为25.5~34.5 GPa，计算模型的混凝土弹性模量变化增量为1 GPa，共10 个混凝土弹性模量值；对基础厚度和混凝土弹性模量组合起来的共21×10=210 个模型进行分析，得到燃机基础在各类基础厚度和混凝土弹性模量下的动力性能。H 级燃机基础的厚度和弹性模量变化区间如表2所示。

表2 H级燃机基础关键影响因素取值Tab.2 Values of key influencing parameters of H-class gas turbine foundation

2.2 有限元多模型建立

采用AYSYS 参数化建模建立燃机基础的整体模型，将H 级燃机基础厚度设为TH，混凝土弹性模量设为EX，通过参数化改变H级燃机基础的厚度TH和混凝土弹性模量EX，从而获得具有不同参数的H级燃机基础模型。燃机基础模型中基础底板及支墩采用SHELL43 单元模拟；设备质量采用MASS21单元模拟；设备转子质量点与基础台板之间采用通过设为刚性杆的BEAM4 单元连接；桩基采用COMBIN14单元模拟水平和竖向三向的刚度；燃机动扰力和振动控制节点为Node4001~Node4004。根据相关实际地勘报告及《动力机器基础设计规范》（GB 50040—20）规定计算，混凝土灌注桩的单桩竖向动刚度为kv=1.33×106kN/m，单桩水平动刚度为kh=1.86×105kN/m。钢筋混凝土密度为2.5×103kg/m3，泊松比为0.2；重力加速度为9.81 m/s2。燃机基础有限元模型如图3所示。其中，X轴为基础纵向，Y轴为基础竖向，Z轴为基础横向。

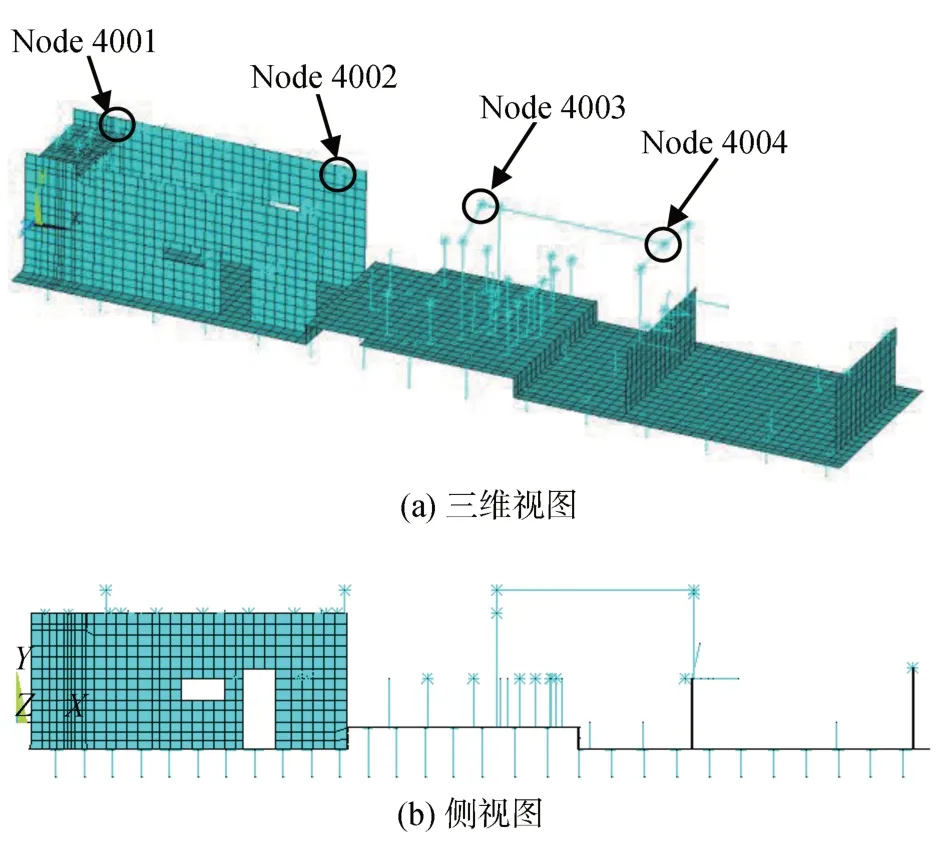
图3 H级燃机基础有限元模型Fig.3 Finite element model of H-class gas turbine foundation

3 多模型模态分析

模态分析作为结构动力分析的基础，其能反应出结构自身固有的振动特性。本文对燃机基础不同基础厚度和混凝土弹性模量的多个模型进行模态分析，得到燃机基础的自振频率、振型与模态质量参与系数等模态信息，可初步判断基础厚度和混凝土弹性模量对燃机基础自身动力特性的影响。在ANSYS 软件中采用分块兰索斯法进行模态分析，提取出燃机基础前50 阶的模态信息，选取基础厚度分别为1.5 m、2.5 m、3.5 m 和弹性模量分别为25.5 kN/mm2、31.5 kN/mm2、34.5 kN/mm2的燃机基础模态计算结果，部分模态频率如表3所示。

燃机基础的第一阶频率为5.16~5.46 Hz，由基础厚度和混凝土弹性模量变化带来的频率变化幅度大约为5%。燃机基础的频率随着基础厚度的增加而减小，随着弹性模量的增加而增加。同时，燃机基础的频率和振型呈现出一定的相似性，其随着基础厚度和混凝土弹性模量的改变在一定范围内变化，并未出现过大变化。燃机的额定运行频率fm=50 Hz，燃机基础的部分频率（主要在17 阶到20 阶之间）处于45 Hz 和55 Hz 之间，此时自振频率与燃机基础的额定运行频率相近，为避免燃机基础因共振现象而产生过大振幅［11-12］。因此，需要对基础在正常运行频率10%范围内进行谐响应分析，并控制基础各控制点的振幅情况，以保证基础在正常运行状态下具有良好动力性能。

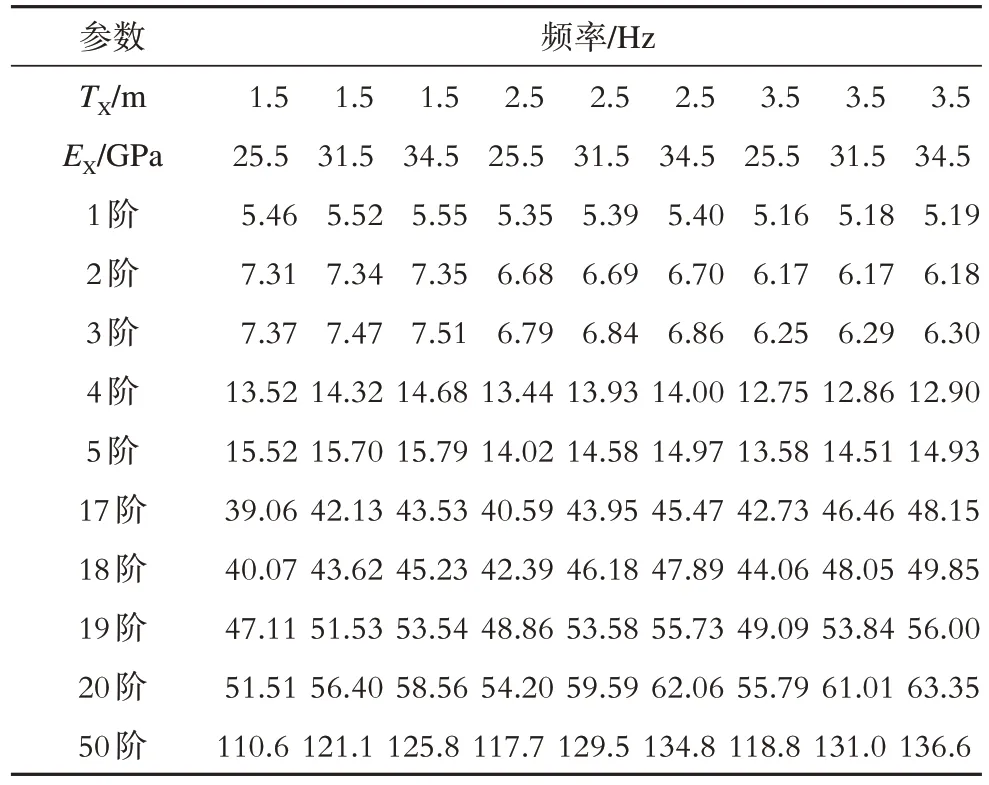
表3 H级燃机基础不同模型模态频率Tab.3 Modal frequencies of different models of H-class gas turbine foundation

4 燃机响应面分析

为建立H 级燃机基础动力性能响应面关系，在ANSYS 软件中对不同基础厚度（1.5 m~3.5 m）和混凝土弹性模量（25.5~34.5 GPa）的模型进行正常运行频率10%范围内（45 Hz到55 Hz）的谐响应分析，每个模型分别提取各单独扰力工况下转子节点的三个方向振幅，按同一方向扰力各节点同一方向振幅的平方和开方（SRSS）求得该模型该方向的控制振幅，并选取每个模型控制振幅中的最大值作为该模型的最大控制振幅［13］。因此，对应210 个不同基础厚度和混凝土弹性模量模型得到210 个最大控制振幅，将基础厚度、混凝土弹性模量和最大控制振幅绘制在三维坐标中，并拟合出最大控制振幅与基础厚度、混凝土弹性模量之间的响应面关系如图4 所示。图中，X轴为混凝土弹性模量EX（GPa），Y轴为基础厚度TH（m），Z轴为最大控制振幅（μm）。

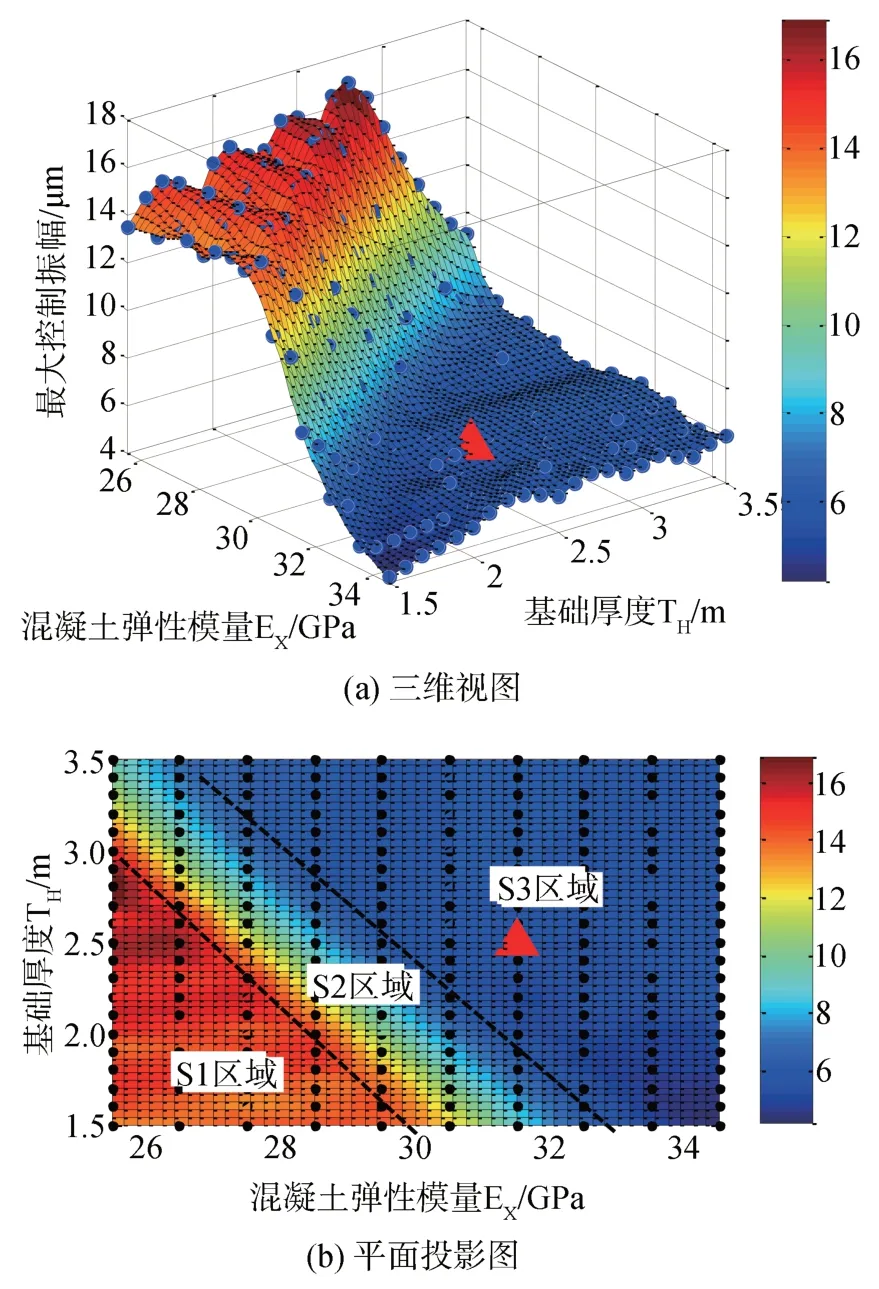
图4 H级燃机基础最大控制振幅响应面图Fig.4 Response surface of the maximum control ampli⁃tude of the H-class gas turbine foundation

由图4 可知，H 级燃机基础最大控制振幅与基础厚度、混凝土弹性模量之间的响应面呈现出S 型曲面特征，两端相对较平，中间增长较快。根据响应面呈现出的特征，将燃机基础最大控制振幅响应面划分为S1，S2 和S3 三个区域。三个区域具有的特征如下：

1） 燃机响应面S1 区域为高振动区域，即0.333EX+TH≤11.5区域。该区域基础厚度和混凝土弹性模量均相对较小，基础的质量和刚度较小，对应的最大控制振幅较大，最大控制振幅达16.8 μm 非常接近振动幅值限值17.1 μm，并较小范围内的调整基础厚度和混凝土弹性模量对基础的动力性能改善较小，若燃机基础处于该区域内，应注重燃机基础的动力分析，保证基础的动力性能满足规范标准要求。

2）燃机响应面S2 区域为振动快速增大区域，即11.5＜0.333EX+TH≤12.5 区域。该区域基础的最大控制振幅对于基础厚度和混凝土弹性模量均较为敏感，最大控制振幅的变化范围为6~14 μm，基础的最大控制振幅随基础厚度和混凝土弹性模量的增大而减小，处于该区域内的燃机基础应同时控制基础厚度和混凝土弹性模量，以考虑其各自变化对基础动力性能的影响。

3） 燃机响应面S3 区域为低振动区域，即0.333EX+TH＞12.5区域。该区域基础有较大的质量和刚度，基础的最大控制振幅均较小，大约为5 μm，燃机基础具有相对稳定和富裕的动力性能，较小范围内的调整基础厚度和混凝土弹性模量依然能够保证燃机基础的动力性能处于优良位置，处于该区域内的燃机基础具有良好的动力性能，并能够抵抗实际工程中因相关参数变化而对动力性能的影响。

H 级燃机基础实际工程设计中根据动力和静力以及施工条件，选定基础厚度为2.5 m，混凝土采用C35，弹性模量为31.5 GPa。其动力性能的最大控制振幅为图4响应面图中的红三角位置，该点位于响应面S3区域，最大控制振幅为5.84 μm＜17.1 μm（限值），同时其在靠近S2 区域位置，使得其在基础设计上具有一定的经济合理性，同时具有较低的最大控制振幅和富裕的动力性能，是较优的H 级燃机基础设计方案。

为了更清晰的了解具体燃机基础在各工况下的振动情况。按实际工程H级燃机基础TH=2.5 m，EX=31.5 GPa。在相应燃机不平衡扰力作用下，其各转子控制点的部分振幅值如图5 所示。燃机基础最大振幅出现在电机端节点4002，运行频率54 Hz 时最大振幅为5.84 μm＜17.1 μm（限值）。在额定转速50 Hz 频率时，燃机基础控制点的最大振幅均小于2 μm，燃机基础的动力性能能够满足国际标准和厂家的要求。

5 动扰力和阻尼比敏感性分析

5.1 动扰力敏感性分析

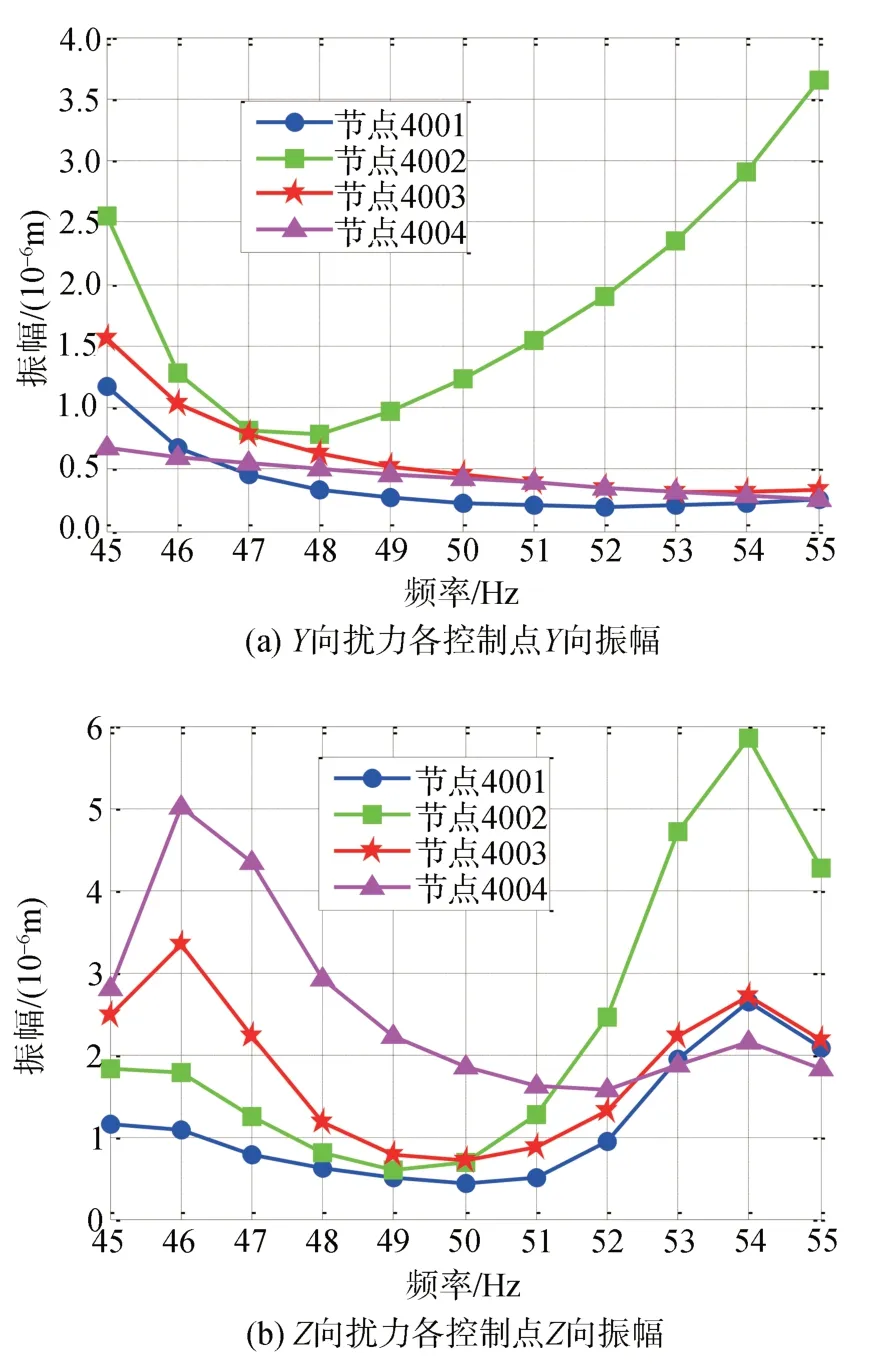
图5 燃机基础各转子控制点振幅值（TH=2.5 m，EX=31.5 GPa）Fig.5 Amplitude of each rotor control point of gas turbine foundation（TH=2.5 m，EX=31.5 GPa）

燃机基础在计算振动线位移时，一般应采用机器制造厂提供的动扰力值。缺乏资料时，可以根据动平衡等级按相关规范确定［14］。根据国际ISO 1940—1 Table 1 动平衡等级标准，燃机转子动平衡等级为G2.5。在进行动力分析未提供动扰力时，保守做法常常可以按动平衡等级G6.3 计算动扰力，G6.3动扰力是G2.5动扰力的2.52倍，扰力在这个区间变化很大，对结果有着不可忽视的影响。分别取动平衡等级 G2.5，1.5 倍 G2.5，2 倍 G2.5，2.5 倍 G2.5 和G6.3计算动扰力对燃机基础进行动力分析，阻尼比取0.02。取振幅最大的Z向扰力节点4002 不同动扰力下Z向振幅如图6所示。

由图6可知，节点4002在G6.3的动平衡等级下最大的Z 向振幅发生在54 Hz 为14.72 μm＜17.1 μm（限值），相对于G2.5 的峰值5.84 μm 增大了2.52倍，并等于动扰力增大倍数。因此，燃机基础控制点的振幅随着动扰力的增大而增大，并且振幅增大的比例与动扰力增大的比例相等。这里取G6.3计算的最大振幅仍能够满足振幅控制标准，燃机基础具有较好的动力性能。

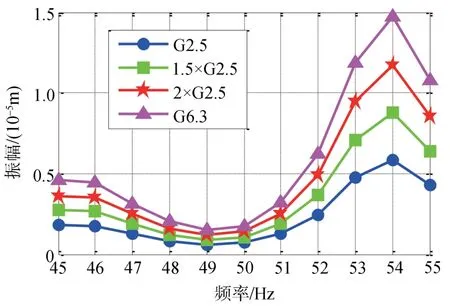
图6 Z向扰力节点4002不同动扰力下Z向振幅Fig.6 Z-direction displacement amplitude of node 4002 under different Z-direction unbalance force

5.2 阻尼比敏感性分析

阻尼对燃机基础动力分析结果影响很大，阻尼比参数的设定，往往是关注的重点［15-16］。美国标准ACI 351.3R—18 中7.2.3.2 条建议混凝土结构的阻尼比取0.02，我国最新发布的《动力机器基础设计标准》GB 50040—2020 中B.1.7 条也对阻尼比的取值由原来的0.062 5 改为了0.02~0.062 5 区间，并提及当振动扰力值小于转子动平衡等级G6.3对应的荷载时，阻尼比宜取小值。动规中阻尼比取值范围区间变大，为研究不同阻尼比带来的影响，分别取阻尼比0.02，0.03，0.04，0.05，0.062 5对燃机基础进行动力分析，动平衡等级取G2.5。取振幅最大的Z向扰力节点4002不同阻尼比下Z向振幅如图7所示。

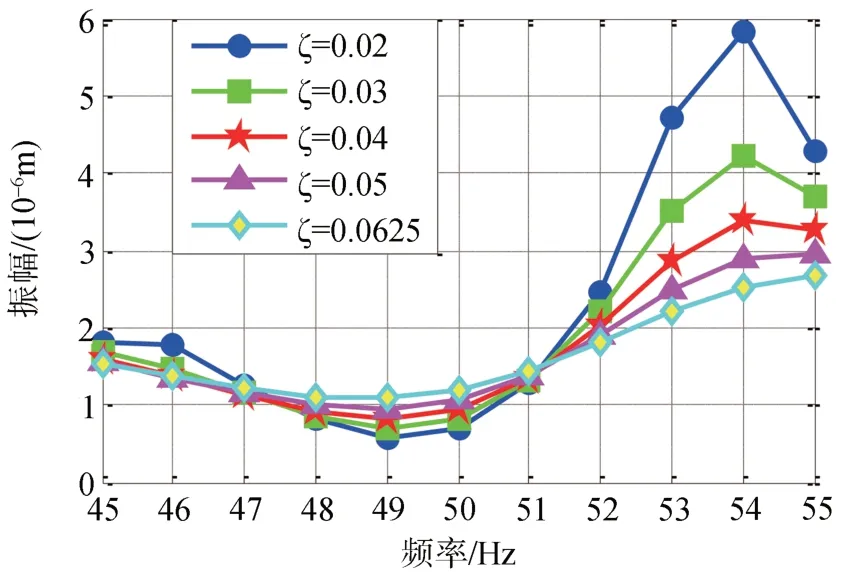
图7 Z向扰力节点4002不同阻尼比下Z向振幅Fig.7 Z-direction displacement amplitude of node 4002 under different damping ratio

由图7 可知，节点4002 在50 Hz 处阻尼比为0.02 时Z向振幅为 0.697 μm，阻尼比为 0.062 5 时Z向振幅为1.188 μm，振幅随着阻尼比的增加不但未减小还增大了1.7 倍；节点4002 在54 Hz 处阻尼比为0.02时Z向振幅为5.84 μm，阻尼比为0.062 5时Z向振幅为2.528 μm，振幅随着阻尼比的增加而减小为原来的0.43 倍。因此，阻尼变化带来的振幅变化不再是单调的，而是跟整个结构体系和动力特性相关，阻尼的增大可能增大也可能减小其振幅。

6 结 论

通过有限元软件ANSYS 参数化建模，选取不同的燃机基础厚度、混凝土弹性模量、动扰力和阻尼比建立不同的H 级燃机基础整体模型，并进行正常运行状态下的谐响应分析获得每个模型的最大控制振幅，清晰地展示了H 级燃机基础在不同参数变化下的动力振幅的变化特征。

1）燃机基础的第一阶频率为5.16~5.46 Hz，由基础厚度和混凝土弹性模量变化带来的频率变化幅度大约为5%。

2）H 级燃机基础最大控制振幅与基础厚度、混凝土弹性模量之间的响应面呈现出S 型曲面特征，并可根据响应面呈现出的特征，划分为S1 高振动区域，S2 振动快速增大区域和S3 低振动区域三个区域。

3）燃机基础实际工程参数计算的最大控制振幅为5.84 μm，满足国际标准和厂家的17.1 μm 限值。并位于响应面S3 区域，具有较低的最大控制振幅和富裕的动力性能。

4）燃机基础控制点的振幅随着动扰力的增大而等比例增大；而阻尼变化带来的振幅变化不是单调的，阻尼的增大可能增大也可能减小其振幅。