基于连续-非连续方法的高填方边坡变形稳定性分析
司宪志,宁 宇,石 崇*,黄青富,张一平
(1.河海大学 岩土工程研究所,江苏 南京 210098;2.中国电建集团昆明勘测设计研究院有限公司,云南 昆明 650051)
我国西南地区多为山地丘陵地貌,在这些区域进行机场建造时,为制造出合适的场地条件和净空条件,势必会进行深挖高填工作,产生大量的高填方边坡[1],同时山地及丘陵地带复杂的地质条件,也给机场建设的安全性带来了挑战,填方地基及高填方体的稳定性问题成为山区机场建设中存在的核心问题[2],加强对该高填方边坡稳定性的研究,寻求科学、合理、有效的评价及防治措施,具有重要的现实意义。数值模拟由于其成本低、效果明显的特点被广泛地应用于边坡稳定性分析[3]中,在连续数值仿真方法方面:陈正东[4]等基于有限差分软件FLAC3D软件,建立了三维边坡数值计算模型,研究了开挖后的边坡体的位移变形特征,并据此对开挖后的边坡进行了稳定性评价;潘网生[5]等基于FLAC3D拉格朗日快速差分算法模拟煤层开挖,揭示边坡变形过程及其滑动机理;言志信[6]等以含软弱层的锚固岩体边坡为研究对象,利用FLAC3D软件模拟分析了地震作用下含软弱层岩体边坡两锚固界面剪切作用及其演化。但连续数值方法中单元之间需要公用节点才能合理描述荷载力的传递,所能模拟的变形量有限,当变形增大到一定程度时,单元会发生畸变导致刚度矩阵无法求解,导致计算终止。在非连续数值仿真方法方面:李龙起[7]等利用颗粒流软件PFC2D对土质滑坡在持续降雨作用下的变形发展过程进行模拟研究,揭示了该滑坡的发展及破坏模式;杨忠平[8]等用振动台物理模型试验,结合UDEC离散元分析方法,研究了频发微震作用下典型上覆软弱岩体边坡的累计损伤过程、动力响应特征及破坏模式,Hung[9]等通过有限元分析和离散元分析,探讨了同震滑坡的破坏前机制和破坏后运动过程与初始时间和运动摆度相关的显著特征。离散单元方法中块体或颗粒可以分离,通过每个时间步不断地接触判断更新块体或颗粒的运动方程,不受变形量限制,但是大量的接触判断导致计算速度降低。
综上所述,如果能将连续-非连续耦合数值模拟方法相互结合,潜在破坏区域采用非连续方法模拟,对于基岩部分变形量小不会出现大变形破坏的区域则采用连续数值模拟方法分析,则既能满足计算效率的要求,又不受变形量限制。本文基于连续-非连续理论,通过边界墙耦合方法建立了某高填方边坡连续-非连续数值模型,研究了该边坡在天然工况下拦挡坝的应力分布情况,将强度折减法应用于细观模拟,进行了边坡在降雨工况下的稳定性分析,并求解了边坡的安全系数,分析了边坡在极端工况下可能的变形破坏情况。
1 连续非连续数值模拟方法
1.1 连续-非连续边界耦合
在连续-非连续相互耦合分析中,有限差分软件FLAC用来从宏观上模拟连续区域内的力学行为,而颗粒流软件PFC用来从细观上模拟离散区域内介质的力学行为,两者间的相互耦合依赖于连续区域与离散区域的接触边界,不同区域间的计算数据是借助于Socket O/I接口来进行相互传输与交换[10-11],连续-非连续耦合计算原理见图1。
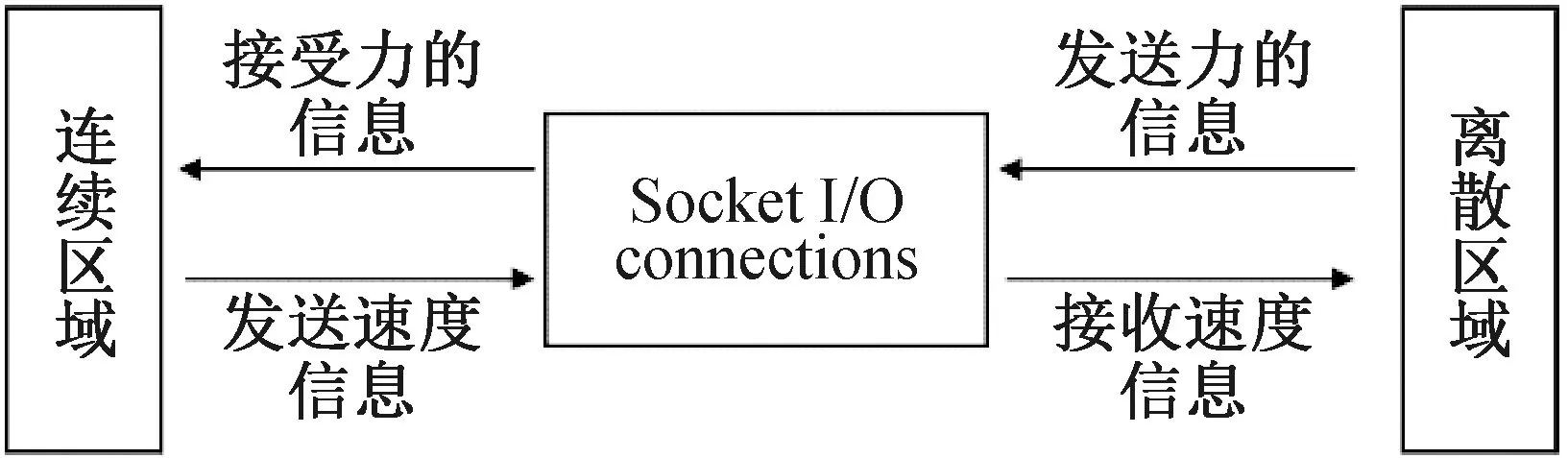
图1 连续-非连续耦合计算原理Fig.1 Calculation principle of continuous-discontinuous coupling method
本文采用基于边界控制墙体的连续-非连续耦合方法,在离散区域和连续区域之间创建边界墙体,离散区域的颗粒运动过程中作用于墙体上的接触力和接触弯矩,采用等效力的方法分配到边界墙体的顶点上,进而将力的信息传递给连续区域的单元,这些力参与到连续区域的有限差分法分析,同样连续区域的运动也会带动边界墙体的运动,进而将位置和速度通过边界墙传递给离散区域,由此实现离散区域与连续区域的耦合计算。
1.2 强度折减法
强度折减法通常应用于计算边坡的安全系数,它是通过逐渐减小边坡体材料的强度参数,从而使边坡体进入到临界破坏状态来求解安全系数。对于Mohr-Coulomb破坏准则来说,安全系数F根据下面的方程来定义:
(1)
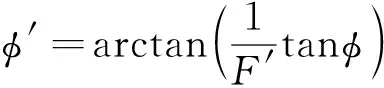
(2)
式中c′为折减后的粘聚力;φ′为折减后的内摩擦角;F′为折减系数。
通过不断调整边坡的岩土体强度指标,即内聚力c和内摩擦角φ,然后对边坡进行稳定性分析,随后通过不断增加折减系数,进行一系列的计算直至边坡达到极限平衡状态,这时候得到的折减系数即为安全系数[12]。
2 工程应用
2.1 工程概况
现拟建某高填方机场,场区高差近400 m,海拔1 500~1 900 m,本期规划机场设计标高1 743 m,挖方量约1 655×104m3,最大挖方高度约70余米,填方量约1 457×104m3,最大填方高度70余米。由于填方高度较大,存在的主要工程地质问题为高填方边坡的稳定性问题以及不均匀沉降问题。
2.2 计算模型与条件
基于以上工程地质状况通过FLAC3D与PFC对NPH3剖面建立连续非连续耦合模型,三维模型尺寸为280 m×8 m×162 m,如图2所示,模型分为基岩、坝体、风化带和土石堆积四部分。土石堆积体用离散元颗粒表示,生成颗粒33 600个,颗粒的直径分布在0.4~0.8 m之间,土石混合体部分颗粒的孔隙率为0.55,颗粒间的接触采用接触粘结模型。挡土坝和基岩由于变形较小,故采用连续单元模型,由于单元的尺寸会对计算结果产生影响,网格密度越高计算结果越精细,但密度过高的网格,其计算效率也越低,为保证合理的计算效率,依据文献[13-15]中相同尺度的模型取单元尺寸大小,单元网格尺寸应取2~5 m,本模型中取3 m,通过ANSYS划分网格后再将模型导入FLAC3D中,共生成单元网格7 897个,单元节点12 225个,对连续区域的模型使用Mohr-Coulomb准则,模型的约束条件设置为左右两侧约束水平位移,底边固定,模型的宏细观参数标定如表1所示。
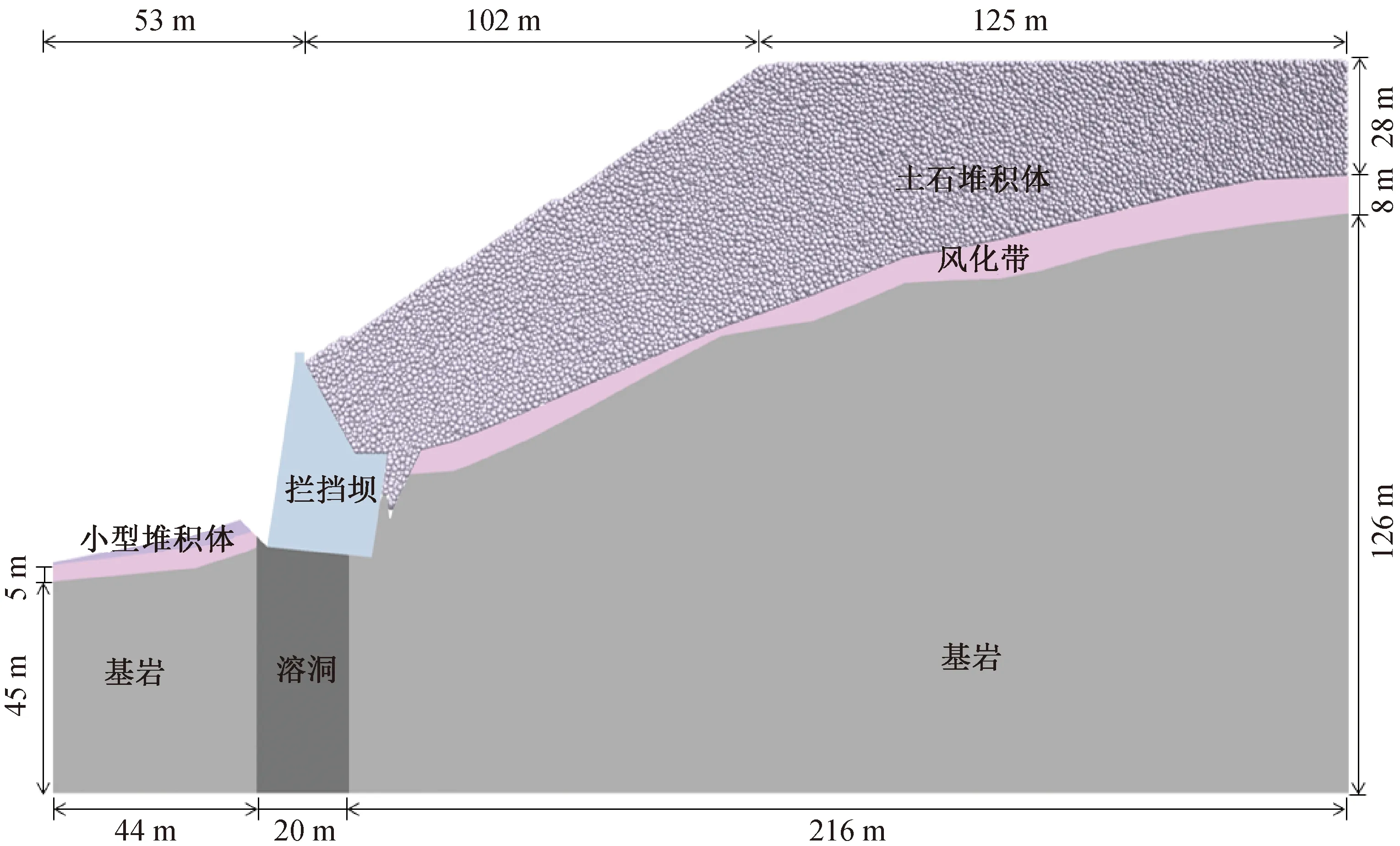
图2 三维数值模型Fig.2 3D numerical model

表 1 数值模型岩土体宏细观参数
3 结果分析
3.1 天然工况
对建立的连续-非连续耦合模型赋予表1所示的宏细观参数,并使其在自重下平衡,最终得到的天然工况下土石堆积体力链分布如图3所示,由于自重作用,堆积体底部力链较为粗壮,顶部力链相对稀疏,在堆积体和风化岩的接触界面,由于接触界面并不为水平,堆积体有相对滑动趋势,但是在坝体的作用下并无位移,因此堆积体与坝体接触部位力链相对粗壮,且堆积体右侧力链出现部分张拉力链。天然工况下堆积体的大主应力分布

图3 天然工况下堆积体力链图Fig.3 Stacking force chain diagram under natural working conditions
如图4所示,由于堆积体的作用,坝体左下角出现应力集中,最大主应力为3.2 MPa。
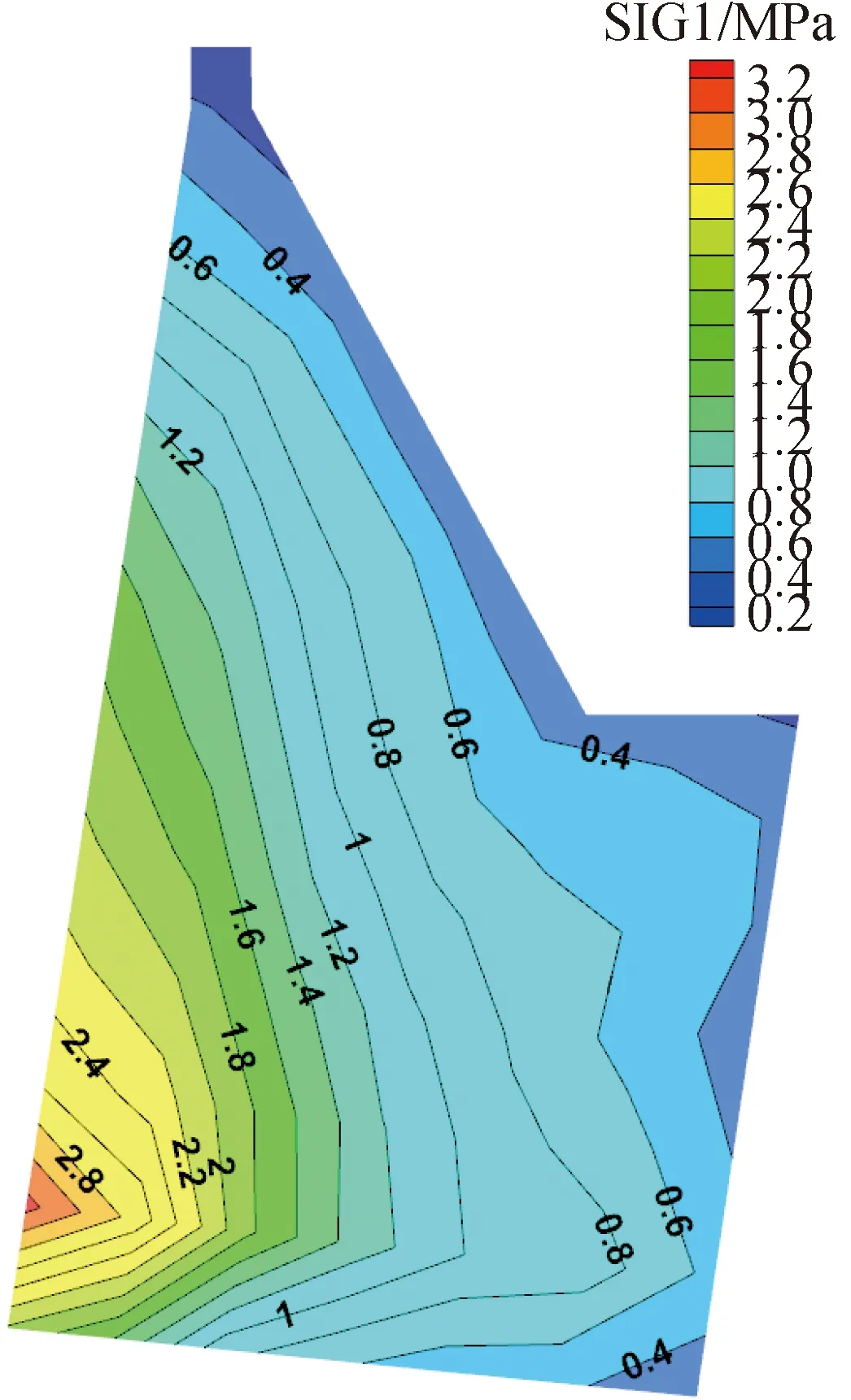
图4 拦挡坝坝体的大主应力等值线图Fig.4 Contour map of high principal stress of retaining dam
3.2 降雨工况
在降雨条件下,降雨过程中及降雨后雨水渗透土体边坡,会引起坡体非饱和带的土体基质吸力降低,由于雨水向下渗透以及地下水位的升高,会导致岩土体的容重发生变化,同时由于水对岩土体的软化作用,使得岩土体的物理力学参数降低[16-18],此外水会对土体产生渗流力与浮力的作用,因此边坡体内的渗流场的变化会引起应力场的变化,同时渗流场的变化也会相应地影响到边坡体中的应力场,水的流动与土体的变形是相互制约相互作用的,在模拟中实现降雨中应力场与渗流场的耦合过程较为复杂,因此为简化降雨工况,将降雨过程简化为对土石堆积体的细观参数进行折减,表2[19-26]统计了近年来8例滑坡中土体饱和状态及天然状态其物理力学参数的折减百分比,土体参数的折减范围在4%~29%,将各案例中土体参数的折减百分比通过气泡图来展示(图5),可见折减百分比大部分在10%~20%,所统计滑坡土体参数折减的平均值在15.45%左右,对于宏观土体应对其内聚力及内摩擦角进行折减,对于土体颗粒的细观参数,根据文献[11,27]的研究,并依据工程经验,应对离散颗粒间接触的摩擦系数、接触粘结张拉强度和接触粘结强度折减15%。
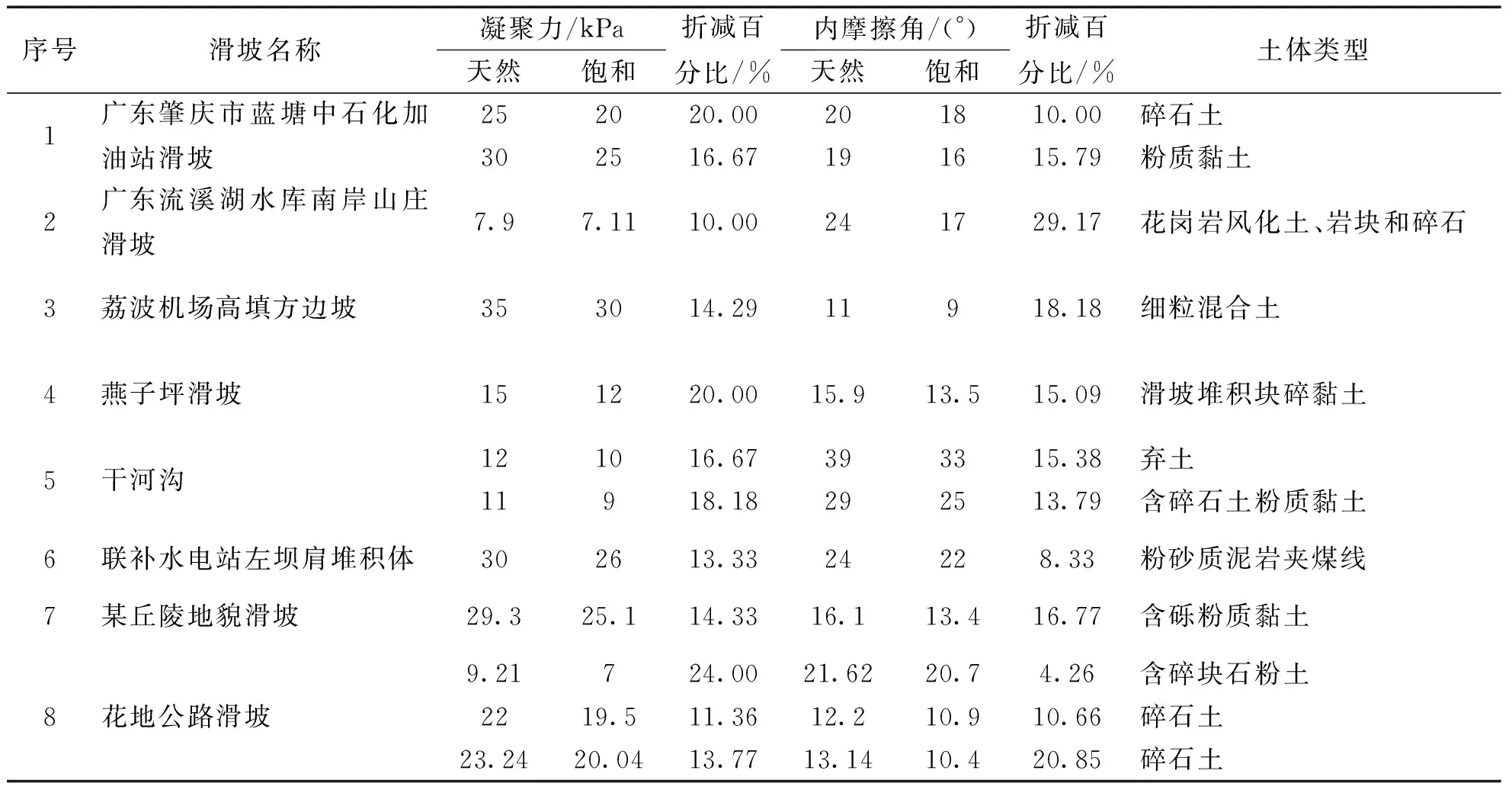
表2 滑坡体材料折减参数
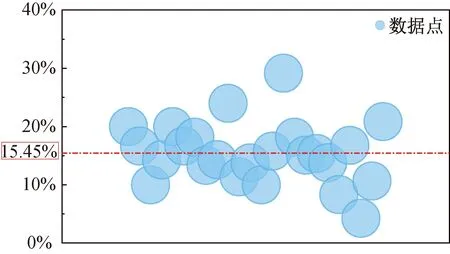
图5 土体参数折减百分比气泡图Fig.5 Bubble chart of reduction percentage of soil parameters
为监测坝体以及堆积体的位移情况,在坝体背面设置监测线,沿堆积体坡面设置监测点,由于监测单独颗粒具有一定的随机性,因此设置数个颗粒团作为一个监测点,并取这几个颗粒的平均位移作为测点的位移,测线及测点分布如图6所示。

图6 测线及测点设置Fig.6 Setup of measuring lines and points
降雨工况下坝体的位移等值线图如图7(a)所示,坝体位移较小,最大位移处位于坝体顶部,为3.8 mm,从坝体顶部至坝体底部位移逐渐减小,坝体背面的位移曲线如图7(b)所示,坝体位移随高程增加而增加,但降雨工况下位移相对较小。

图7 降雨工况下坝体位移Fig.7 Dam displacement under rainfall condition
降雨工况下堆积体的位移如图8(a)所示,最大位移处位于堆积体的顶部,为0.5 m。堆积体坡面沿高程方向的位移曲线如图8(c)所示,堆积体的位移沿坡面从坡底向坡顶逐渐增加,位移与高程基本呈线性相关,出现这一现象的原因是由于降雨工况下堆积体的材料参数折减导致的不均匀沉降。由图8(b) 可见,堆积体的位移主要朝下,在与风化带接触界面角度的影响下,堆积体产生少量沿坡面方向的位移,但在坝体的阻挡作用下,未产生明显的沿坡面方向位移。
3.3 强度折减
利用强度折减法对堆积体的力学参数进行折减以寻求边坡安全系数,对堆积体颗粒间接触的摩擦系数、接触粘结张拉强度和接触粘结强度进行折减,按照二分法依次折减,若堆积体出现明显滑动面或塌落,则判定为破坏,当折减至临界破坏状态,则取安全系数为让模型恰好出现破坏的折减系数。图8为对模型采用二分法折减时堆积体的位移云图,当折减系数为2.0时,堆积体出现明显塌落,并沿图示曲线滑塌,则调整折减系数为1.50,堆积体并无明显滑动面,继续折减直至堆积体恰好出现破坏,如图9(d)和图9(f)所示,当折减系数为1.60时,堆积体恰好出现滑动面,当折减系数为1.59时,堆积体无滑动面出现,因此判定堆积体的安全系数为1.60。
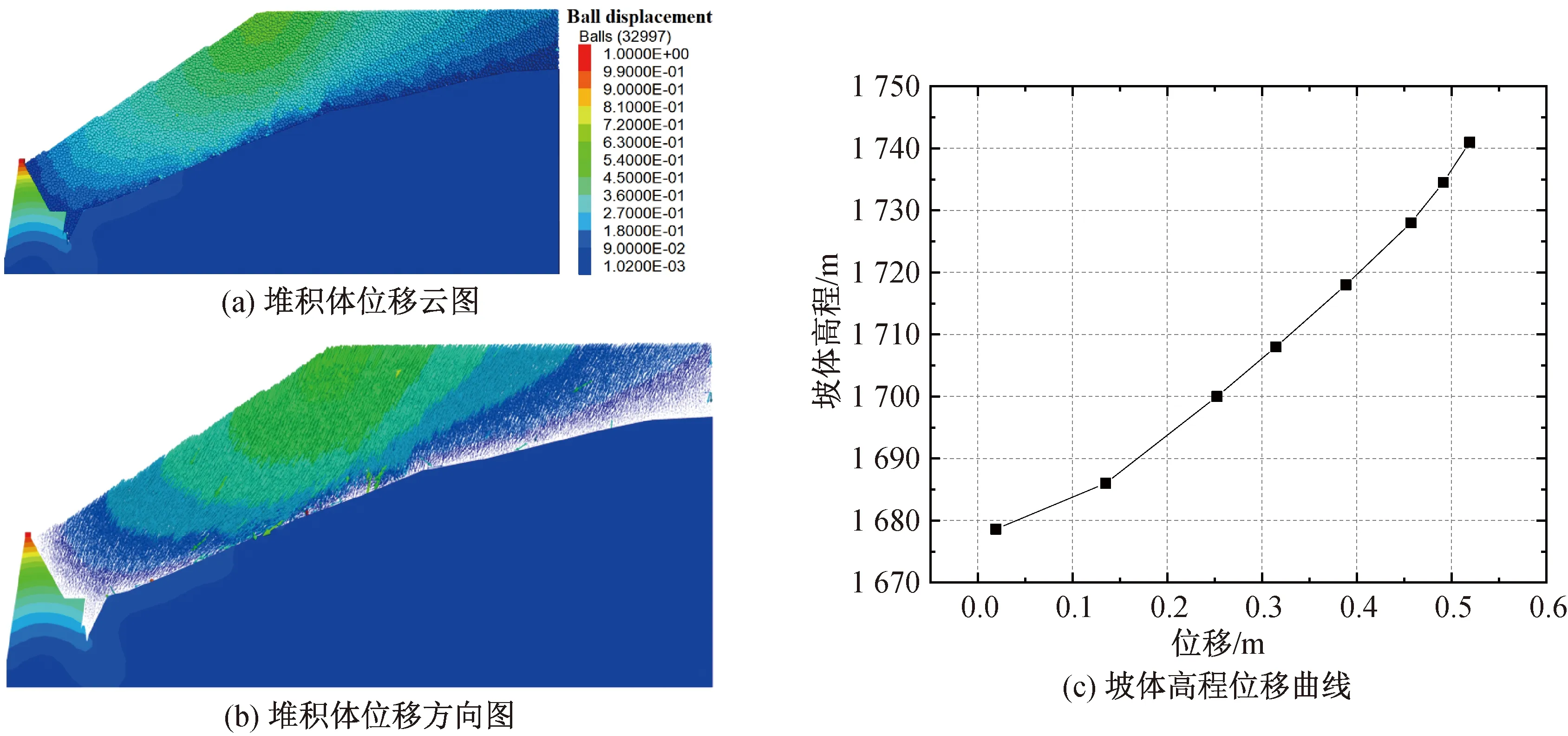
图8 降雨工况下堆积体位移Fig.8 Displacement of accumulation body under rainfall condition
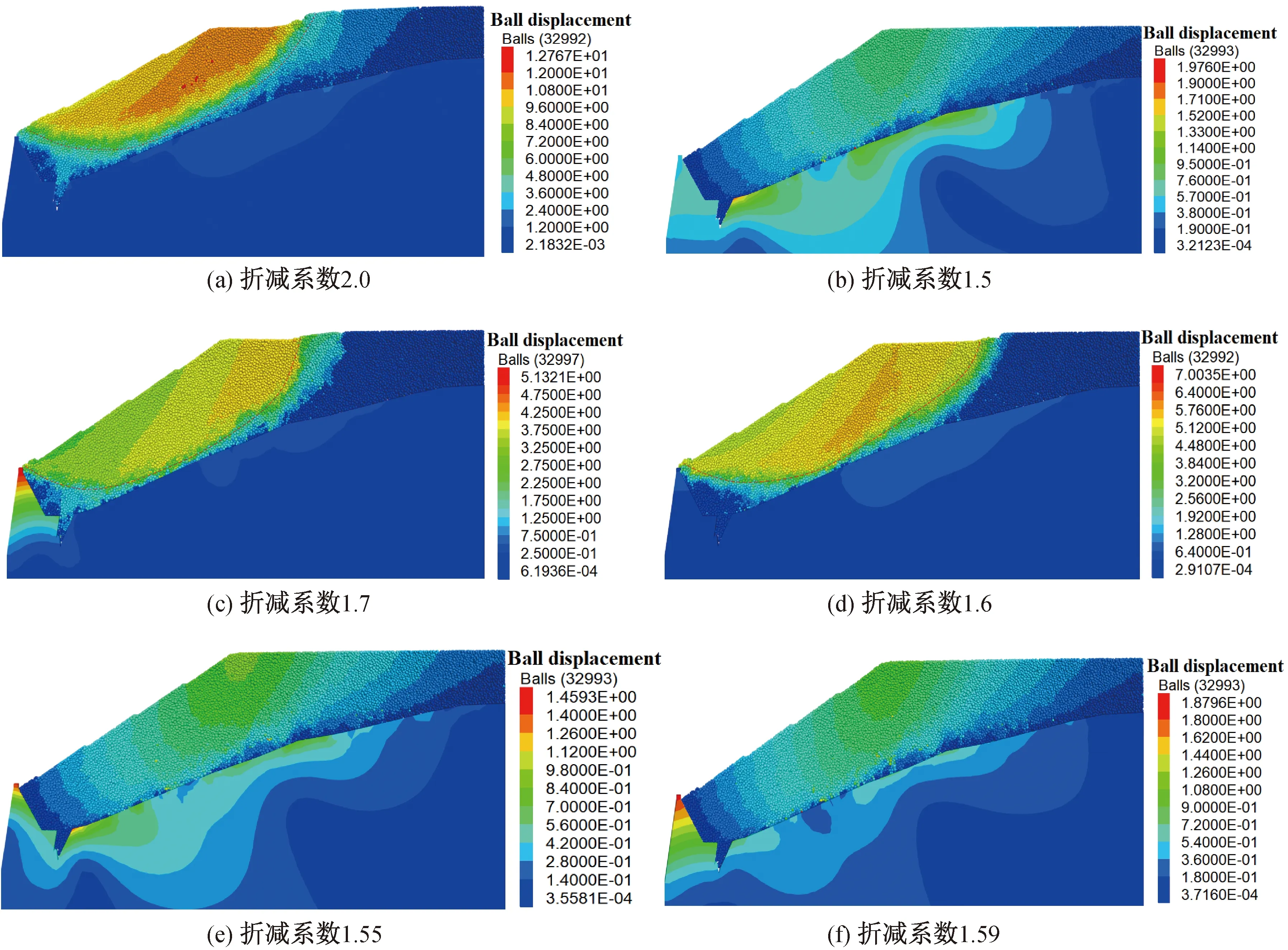
图9 不同折减系数下堆积体位移云图Fig.9 Displacement nephogram of accumulation under different reduction factors
当折减系数为1.60时,堆积体颗粒的位移情况如图10(b)所示,堆积体颗粒出现塌落,并沿图示曲线滑塌,在坝体顶端滑出,但坝体无明显位移,颗粒的位移方向如图10(a)所示,滑塌区域的颗粒位移方向基本一致,位移最大的区域位于滑塌体中部,堆积体颗粒的力链如图10(c)所示,滑塌区域顶部(如图所示方框内)力链出现断裂,可见滑塌区域与后方堆积体出现明显的错动;堆积体颗粒的接触破坏模式如图10(d)所示,不同的接触状态表明不同的接触破坏方式。从图中接触粘结破坏模式可以看出,堆积体的滑动面附近大部分颗粒接触处于非粘结状态和由剪切破坏导致的接触非粘结状态,产生的裂隙大部分位于滑动面附近,与实际滑坡相符合。
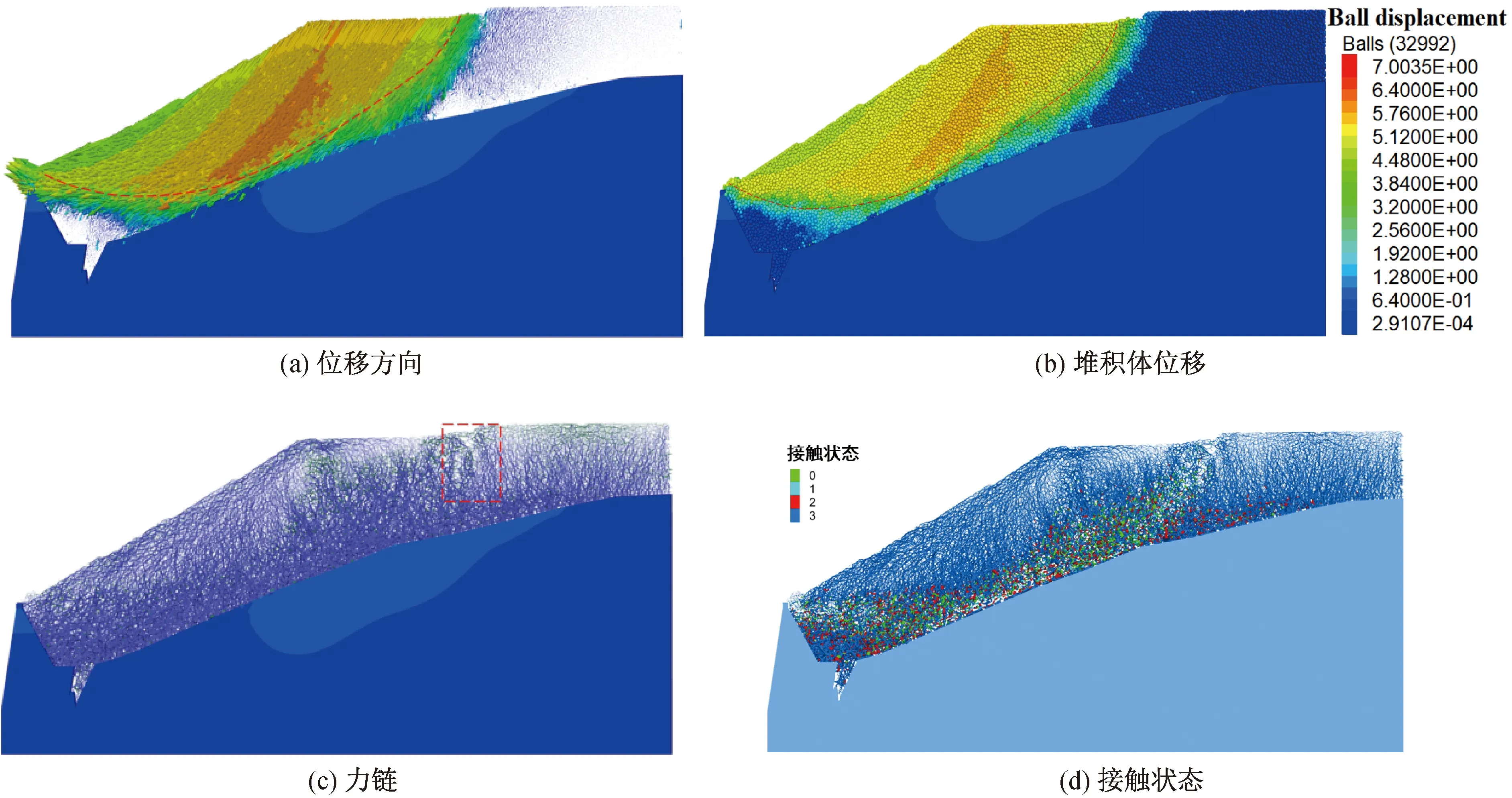
注:图例中0表示相邻颗粒处于非粘结状态,1表示接触非粘结并且是由于张拉导致破坏,2表示接触非粘结并且是由于剪切破导致产生,3表示接触处于粘结状态且粘结完好无损。图10 折减系数为1.60时颗粒情况Fig.10 Particle size distribution with reduction factor of 1.60
堆积体坡面沿高程方向的颗粒位移情况图11所示,坡面位移最大的区域位于堆积体顶部,为3.78 m,位移最小的区域位于堆积体坡面底部,为1.64 m,除堆积体底部与坝体接触区域外,堆积体坡面的位移基本与高程成正比,结合图10(b),高填方边坡在极端情况(如持续高强度降雨、地震等)下,潜在失稳区域更大,发生失稳时滑面更深,范围更广,更应做好边坡的支挡工作。
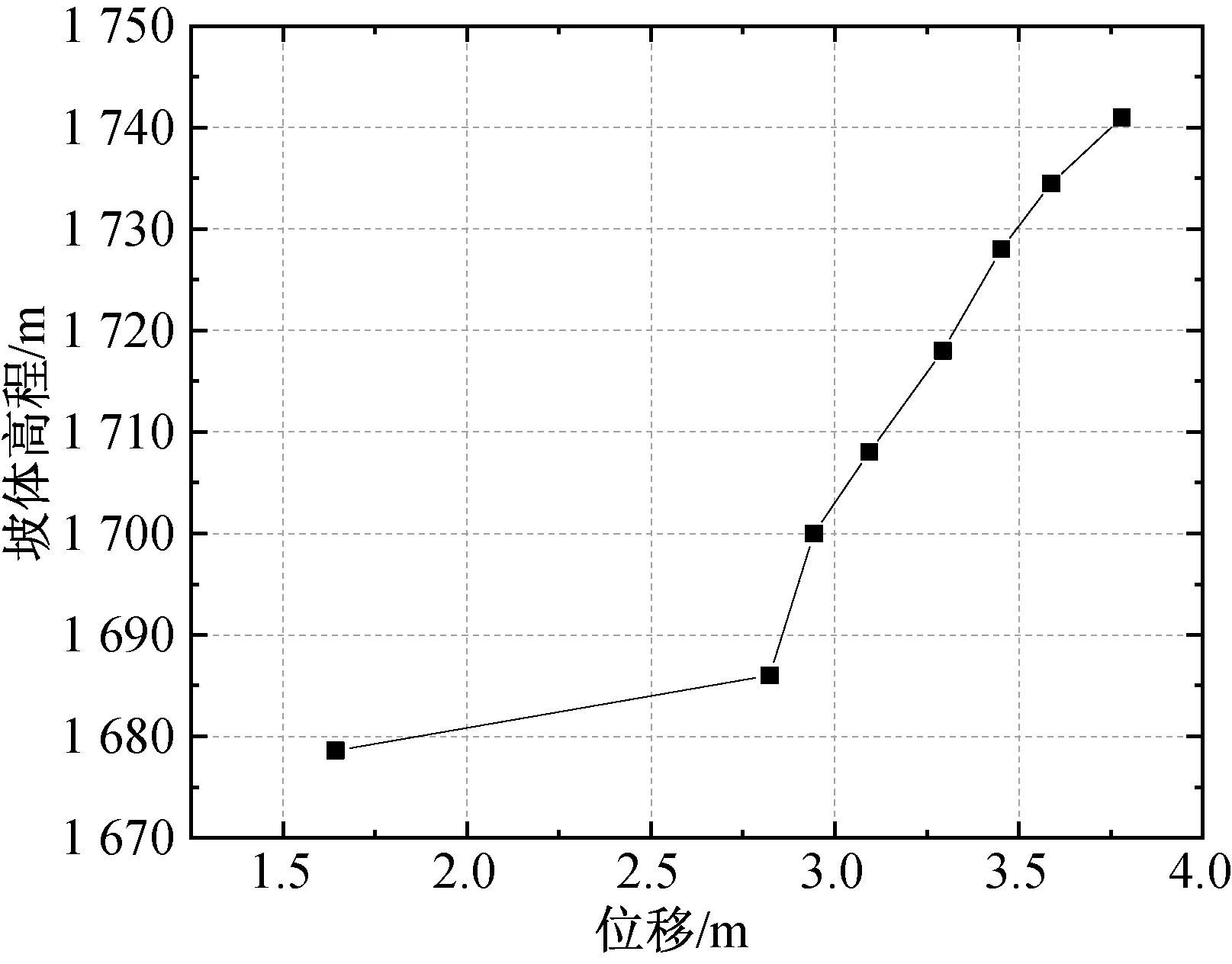
图11 折减系数为1.60时坡面高程位移Fig.11 Elevation displacement of slope with reduction factor of 1.60
4 结论
本文基于连续-非连续耦合数值模拟方法,依据边界墙耦合理论建立PFC-FLAC耦合模型,并通过强度折减法对边坡进行了稳定性分析,得到结论如下:
1) 通过该方法验证了连续-非连续耦合分析在边坡工程中的应用可行性,运用连续-非连续方法分析可以更直观高效地评估边坡稳定性。
2) 通过强度折减法求解了某工程高填方边坡的安全系数,并研究了其在降雨工况下和极端工况下的边坡稳定性情况,得出在降雨工况下边坡较为稳定,在极端工况下边坡产生大范围滑塌,滑塌区域沿坝体顶部滑出。
3) 高填方边坡在极端工况下产生滑坡时,会产生更大的滑坡区域,更应做好对高填方边坡的支护工作。

