GPS基线投影变形和基线边检查的研究
赵健
河北中核岩土工程有限责任公司测绘地理信息事业部 河北石家庄 050000
当前CGCS2000大地坐标系统成为官方要求使用的唯一国家标准坐标系统。在平面坐标系统方面,我国大比例尺地形图均要求采用高斯投影,GPS基线元素经两次空间转换投影到高斯平面上,其投影产生的变形问题无法避免,投影变形的大小直接关系到GPS控制网的整体精度。当GPS控制网完成平差及精度评定后在对可通视的GPS基线边长进行检查时,观测边长本身的精度也是衡量GPS基线边长精度的主要因素,因此成功的解决投影变形问题及GPS静态边长检查问题,是评定GPS控制网精度的最关键的两个因素。下面就这两种因素作具体研究说明。
1 因素研究说明
1.1 投影变形
1.1.1 投影变形概念
在实际工程应用中,无论地形图的测设还是施工图的设计均是建立在平面直角坐标的基础上。当椭球面上的点位以平面直角坐标表示时,必不可少的步骤便是投影,由于椭球面是一个凸起的不可直接伸展成平面的曲面,如果将曲面上的元素投影到平面上,必然同原来的距离、方向、角度及图形产生差异,因此无论采用何种投影方法,投影变形一定存在。
我国大比例尺地形图一般采用高斯投影。高斯投影的最主要特点是中央子午线上无投影变形,除中央子午线外其他长度变形均大于0。高斯投影模型见图1[1]。
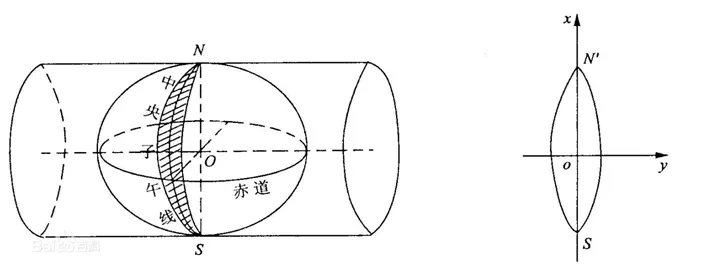
图1 高斯投影模型
1.1.2 投影变形元素
要将椭球体上元素投影到平面上,包括坐标、方向和长度三类问题。当椭球面与平面对应点间的坐标关系已经确定后,相应地,方向和长度的投影关系也即确定。
(1)坐标元素(高斯正反算)。推求高斯投影坐标关系式,是整个投影过程的主要问题。高斯投影坐标分为正算和反算。正算为由L、B求x、y,反算为由x、y推求L、B。正、反算公式分别如下:
①正算公式:

上式中,x、y为正算平面坐标,B、L为纬度、经度,l为经差。
②反算公式:

上式中,B、L为纬度、经度,Bf为垂足纬度。
高斯正反算解释如下:
①正算公式:
正算为已知B、L,求x、y。由于l值不大,因此公式可展开为l的幂级数,并以已知纬度B的函数m作为及系数,公式结果是:

当l=0时,x=X
②反算公式:
反算为已知x、y求L、B。由于y值不大,因此公式可展开为y的幂级数。此时纬度B是要求的,但某点的垂足纬度Bf是已知的,因此公式中的各系数是Bf的函数,结果是:
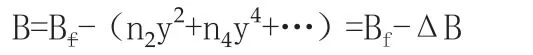
通过对正算、反算公式分析,可知如下特点:①当l为常数时,随着B的增加x值增大,y值减小;又因cos(-B)=cos(B),所以无论B值为正还是为负,y值不变。意思即为,椭球面上除中央子午线外,其他子午线投影后,均向中央子午线弯曲,并向两级收敛,同时对称于中央子午线和赤道[2]。②当B为常数时,随着l的增加,x和y值都变大。所以在椭球面上对称于赤道,投影后仍成为对称的曲线,同时与子午线的投影曲线互相垂直凹向两级。③距离中央子午线越远的子午线,投影后弯曲越厉害,长度变形越大。以上便可以证明高斯投影最重要的特点,即中央子午线上无投影变形,除中央子午线外其他长度变形均大于0,且距离中央子午线越远变形越大。引用参考文献[1]
(2)方向、边长元素.椭球面元素归算到高斯平面直角坐标系会产生方向变形和长度变形。球面三角形经过正形投影后,形状保持了相似性,边长为曲线。椭球面三角形归算到高斯平面直角坐标系要经过以下过程:
①角度归化。地面观测的方向值归算到椭球面。归算过程中需经过垂线偏差改正、标高差改正及截面差改正,即为三差改正。此项改正在一等、二等大地测量中需加以改正,在工程测量中由于控制网精度相较于大地测量较低,基本均为三、四等控制测量,无需改正。
②距离归化。地面观测的距离归算到椭球面。假设平均水准面与椭球面平行,高程会对椭球面长度归算带来影响。地面边长(S0+ΔS)与椭球面越远,即大地高Hm越大,归化到椭球面的边长S变得越短。

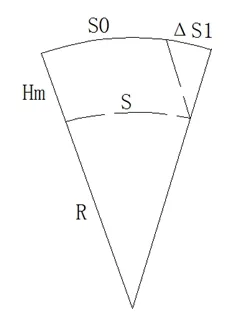
图2 距离归化到椭球面
式中ΔS1-平均水准面长度归化到椭球面所加的改正;
Hm-边长两端大地高平均值;
S-椭球面边长;
R-当地椭球面平均曲率半径。
③经高斯正算,把椭球面坐标转换到平面坐标,再用高斯反算检核。
④两点间大地线归算到平面直线,球面三角形内角归化到高斯平面三角形内角,经过曲率改化(方向改化)计算和子午线收敛角计算。
⑤椭球大地线数据归化到高斯平面所加的改正[3]。
因高斯投影面上除了中央子午线外长度比都大于1,故椭球边长(大地线)归化到高斯平面所加的改正与边长距离中央子午线的远近相关,从椭球面归化到高斯平面的边长变长。以下为投影变形改正公式:

式中ΔS2-椭球面归化到高斯平面所加的改正;
ym-投影边两端y坐标平均值;
S-椭球面边长;
R-当地椭球面曲率半径。
⑥地面测量的边长改化到高斯平面上的近似改正数为ΔS=ΔS1+ΔS2。
1.1.3 抵偿投影变形
根据《工程测量规范》GB50026-2007中第3章平面控制测量第3.1.4节规定,测区内投影长度变形不应大于2.5cm/km,因此在GPS控制网施测中,首先便要根据投影变形是否符合规范要求来解决投影变形问题。下面根据某高速公路隧道控制网实际工程案例予以说明。
(1)控制网网型。
(2)控制点情况。平面坐标系统为2000国家坐标系,高斯平面直角坐标系3°带,中央子午线为117°,高程系统为1985国家高程基准。
(3)投影变形值。以II13-II14、II15-I049两条通视已知起算边为例说明。如果采用国家标准3°带投影,在中央子午线为117°前提下,根据公式(1)、(2)计算可得投影变形值,具体见表1。注意:本案例中点位纬度约为北纬40°左右,故取曲率半径R为6375km。由表1知,当边长归化到参考椭球面上时投影变形超过2.5cm/km,投影到高斯平面上时投影变形超过规范规定2.5cm/km的要求,综合投影变形ΔS亦超过2.5cm/km的规定,无法满足规范要求。因此按照标准3°带投影将中央子午线设置为117°无法实现精度要求[4]。

表1 投影变形值计算
(4)抵偿投影变形措施。理论上抵偿投影变形措施为移动中央子午线及改变高程投影面。下面分步解决。
①移动中央子午线。测区经度平均值约为115°32’,为使测区边长变形最小,理论上应设置中央子午线为115°32’。但因该隧道为东西方向,距离较长,施工单位为两家单位对向施工,最后将在隧道中部实现贯通,为使隧道在贯通面上边长变形最小,同时结合该整段线路控制测量资料,通过综合分析,选择中央子午线为115°40′。通过坐标换带计算可得各控制点在中央子午线为115°40′时的平面坐标,通过公式(2)可求得ΔS2,具体见表2。
由表2可知,当中央子午线移动到115°40′后,高斯投影变形值ΔS2明显小于2.5cm/km,由于地表边长归化到参考椭球上ΔS1变量中只涉及Hm,所以在移动中央子午线后该值并未发生变化,综合变形值远大于2.5cm/km要求,因此只移动中央子午线不能规范要求。

表2 投影变形值计算
②选择抵偿面。当边长规划到参考椭球面上变形值不符合规范要求时,要选择合适的高程抵偿面来消除长度变形误差,为确保ΔS1+ΔS2尽量最小,在ΔS2已知的情况下需确保ΔS1尽量最小。
H0=Ym2/2RmH=H0+Hm
Ym2=(ymax2+ymin2)/2-(测区位于中央子午线一侧)
Ym2=max{|ymax2|,ymin2}/2-(测区横跨中央子午线)(3)
式中H0-测区平均高程面(Hm)高出抵偿高程面的高度;
H-测区抵偿面高程;
ymax、ymin-测区内距离中央子午线的最大、最小距离;
Rm-当地椭球面曲率半径;
测区平均高程已知为1428.581m,Ym需根据测区范围确定,ymax为12195.721m,ymin为8971.259m,经公式(3)计算,抵偿面高出平均高程面的值为8.989m,则有抵偿面高程值为1437.57m。再通过公式1计算此时ΔS1,则有表3。由表3可知,在1437.57m的高程抵偿面上,两条边的变形值均远小于2.5cm/km的规定。由于测区平均高程与抵偿面高程相差不多,当抵偿面选择平均高程面1428.581m时,得到的ΔS1见表4。

表3 抵偿面变形值计算

表4 平均高程面变形值计算
由表4可知,在平均高程面上,边长变形值同选择的高程抵偿面相差极小,因此在工程测量实际应用中,选取测区平均高程面即可满足每千米投影变形值不大于2.5cm的要求。
通过以上案例分析可知,为使边长经参考椭球面改化及高斯投影过程中的投影变形值趋于最小,可以采用移动中央子午线及选择抵偿高程面的方式予以减小或消除。尤其是在高海拔地区,平均高程较大,如果在静态平差过程中投影面选择不准确,将给投影变形带来很大影响。
1.2 GPS基线边长检验
1.2.1 GPS基线边长检验方式
通常情况下,当GPS控制网施测完成后,应对通视边边长进行检核。边长检核一般选用激光测距仪,目前实际操作中均为全站仪。
1.2.2 影响全站仪边长测距精度因素
当使用全站仪对GPS边长进行检查时,影响全站仪测边精度的因素较多,包括测量时间、测站和观测目标周边环境、大气折光影响、加乘常数和棱镜常数改正及气象因素,其中最主要的因素为气象因素。工程测量规范《GB50026-2007》规定,测距应对仪器进行气象改正。测量时间、周边环境、大气折光等因素在选择合适的观测条件时即可削弱其带来的影响,加乘常数可以通过经鉴定的全站仪鉴定报告正确设置。棱镜常数为常量,通过正确的设置即可。以上因素本文不作详述,下面就影响最大的气象改正对边长的影响做具体说明。
1.2.3 全站仪气象改正对测边的影响
全站仪气象改正包括气压、温度改正。下面就两者对测边精度的影响予以分项说明。
(1)气压改正。全站仪在测站开展测边之前应将测站当前气压值输入全站仪。由仪器根据输入气压值完成当前测站的气压改正。下面以某高速隧道控制网为例说明。
图3中,II13-II14、I049-II15为已知边,通过全站仪在设置温度相同气压不同情况下检查的边长值见表5。

图3 控制网网型
通过表5可以大致判断,气压对全站仪边长影响较大。去掉控制点坐标误差、仪器及棱镜对中误差、温度误差,由气压本身带来的误差大致为0.3mm/km每1hpa。测得的边长随着气压的增大而减小。因此在GPS边长检查中和日常施工测量中,正确设置气压值尤为重要,尤其是高海拔地区,需严格按照气压表数据正确改正。
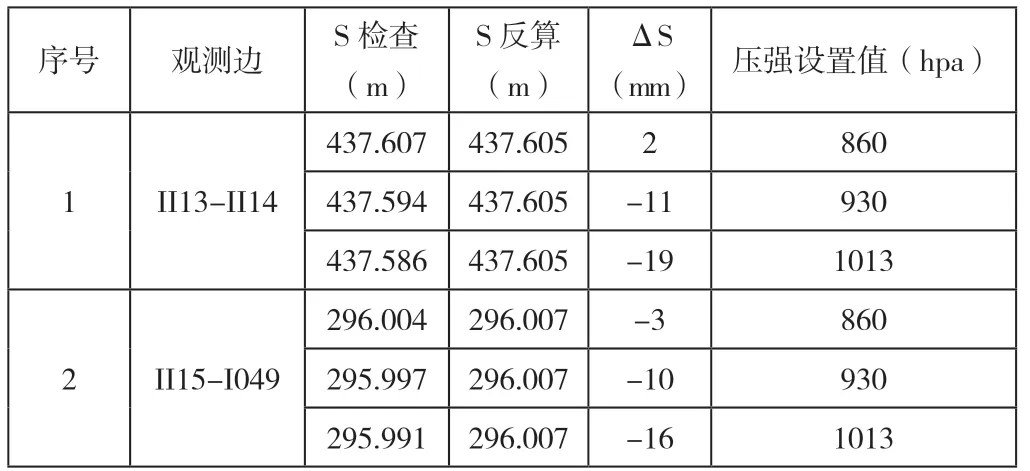
表5 同温度不同压强边长检查值
(2)温度改正。全站仪在测站开展测边之前应将测站当前温度值输入全站仪。由仪器根据输入温度值完成当前测站的温度改正。在输入正确的气温值之前需将全站仪静置在测站温度环境下至少30分钟,尽量避免阳光直射,待仪器内部各机械及电子元器件同当前环境下温度相统一后再行观测。下面仍以某高速隧道控制网为例说明。
图3中,II13-II14、I049-II15为已知边,通过全站仪在设置相同压强不同温度下检查的边长值见表6。

表6 同压强不同温度边长检查值
通过表6可以大致判断,温度改正对全站仪测量边长影响相较于气压改正较小。去掉控制点坐标误差、仪器及棱镜对中误差、气压误差,由温度本身带来的误差大致为1mm/km每1℃。测得的边长随着温度的增大而增大。
由以上可知,在使用全站仪检查GPS边长时尤其是高海拔地区必须正确使用气压计、温度计对气压及温度进行精确改正,尤其是长度超过1km的边长。
2 结语
通过第1章中对所列因素影响及解决措施进行分析,得出以下结论。
2.1 GPS投影变形
控制网施测前应分析测区各控制点东坐标所在位置,也即各控制点距离中央子午线长度范围,将中央子午线移动至测区卯酉圈(东西)方向上大致中央的位置,同时分析测区大地高分布范围,确定合适的抵偿投影面,一般设置测区平均高程面即可。
2.2 全站仪边长检查
全站仪测距之前,务必将测区测站位置的温度值及压强值正确输入全站仪,确保气象改正正确,使全站仪测距误差降到最低,确保对GPS基线边长的检验值正确有效,充分辨识GPS基线边长测距的精度。

