提升轴系扭振分析置信度的建模方法

彭宇明，马健，刘磊，罗振，甘金科

(1.先进驱动节能技术教育部工程研究中心，四川 成都 610031；2.西南交通大学机械学院，四川 成都 610031；3.东风商用车技术中心，湖北 武汉 430056；4.柳州龙杰汽车配件有限责任公司，广西 柳州 545006；5.长安汽车股份有限公司，重庆 400000)

随着国内汽车行业的快速发展，汽车作为代步工具早已普及，相应地，在满足低功耗、低排放的同时，汽车发动机的噪声、振动和平顺性(NVH)也更加受到关注。曲轴作为发动机重要的动力部件，其扭振特性影响发动机的诸多性能。内燃机运转时，曲轴系统受到大小和方向都作周期性变化的力，从而产生强迫振动，这样会给发动机工作可靠性、稳定性和性能带来很大影响，甚至会导致曲轴断裂，引发重大事故[1-2]。

内燃机轴系扭振分析是一个比较复杂的技术问题，影响因素也比较多，国内外许多学者对曲轴系的扭振特性进行了研究[3-5]。台架试验本身易受众多因素的影响，扭振测试的测点往往设置在飞轮端或是自由端等个别位置，难以反映轴系扭振的全貌，且台架试验耗时费力，扭振特性的改进要成品才能体现，不利于配件的改进和提升[6]。CAE技术的快速发展，使得方便快捷地建立曲轴扭振的仿真模型成为可能。目前工程上普遍采用一维仿真模型计算曲轴扭振特性，简单方便快捷，且一个较高置信度的一维扭振模型能很好地反映曲轴实际的扭振特性，具有较高的精度。与一维相比，三维仿真模型虽然能更好地与实际情况吻合，但是由于其需要定义整个发动机结构，以及各个部件之间的非线性连接，对于供应商来说这是难以实现的，最重要的是具有较高置信度的一维仿真模型便可获得可靠的扭振仿真结果，采用三维仿真得不偿失。因此建立一个具有较高置信度的一维扭振仿真模型是分析曲轴扭振特性的基础。

针对单一集中质量模型置信度不高的缺点，本研究提出一种多级校核验证方法，通过不断校核验证以建立具有较高置信度的曲轴扭振仿真模型，依托多层次多角度的三维模型来校正一维模型的精度，大幅度减少试验验证环节。以某直列4缸汽油机为研究对象，利用内燃机多体动力学软件AVL Excite建立了发动机曲轴系统扭转振动的集中质量模型，讨论了对结果影响较大的惯量及刚度参数的计算方法，确定模型刚度、惯量等参数后，根据所得的集中质量模型进行模态分析，并通过一维与三维的逐级模态对比，校核验证所搭建的集中质量模型的置信度。通过强迫振动仿真分析结果与试验数据进行对比，检验此分析方法的准确性和可靠性。

1 扭振理论分析

通常，曲轴的扭振计算是把复杂的曲轴系统简化为一系列由集中质量和弹性轴组成的当量扭振系统。一般要求当量扭振系统的固有频率与实际系统的固有频率相等，并且当量扭振系统的振型应与实际系统的振型相似[7]。

根据牛顿第二定理，建立轴系当量系统扭转振动的动力学微分方程：

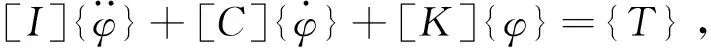
(1)

[C]=[C0]+[Cr]。

(2)

式中：[I]为转动惯量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{T}为激励力矩向量；{φ}为角位移向量；[C0]为外阻尼矩阵；[Cr]为内阻尼矩阵。

当T=0时，计算系统的自由振动，计算结果包括特征值(固有频率)及特征向量(振型)；当T≠0时，计算系统的强迫振动，可以得到各自由度的扭振角位移等。由动力学方程可知，转动惯量和刚度数据的准确获取是计算曲轴扭振的重中之重。

2 曲轴集中质量模型的建立与校核

2.1 集中质量模型

以某4缸汽油机为研究对象，在一维非线性多体动力学软件AVL-EXCITE Designer上通过建立质量-弹簧-阻尼形式的扭振集中质量模型，将曲轴离散为减振器、主轴颈、曲柄臂、曲柄销、飞轮，对发动机曲轴扭振进行分析[11]。首先在子模块Shaft Modeler中根据曲轴的实际结构建立图1所示的多体动力学模型，模型的各个模块应尽可能合理地表达曲轴结构。

图1 曲轴模型

软件根据各个模块输入的惯量、刚度等参数根据图中虚线及黑色编号所示转化为由有惯量无刚度的质量点和有刚度无质量的轴段构成的集中质量模型(见图2)，其中减振器转化成两个集中质量点，曲柄臂的转动惯量一分为二，分别添加到紧邻的主轴颈和曲柄销的集中质量点上。这是进行曲轴扭振分析的基础，同时集中质量模型的正确与否也直接影响了扭振分析结果的准确性。可以说建立准确的曲轴集中质量模型是进行扭振分析最为关键的一步。其中，准确获取各自由度的转动惯量、扭转刚度为重中之重。

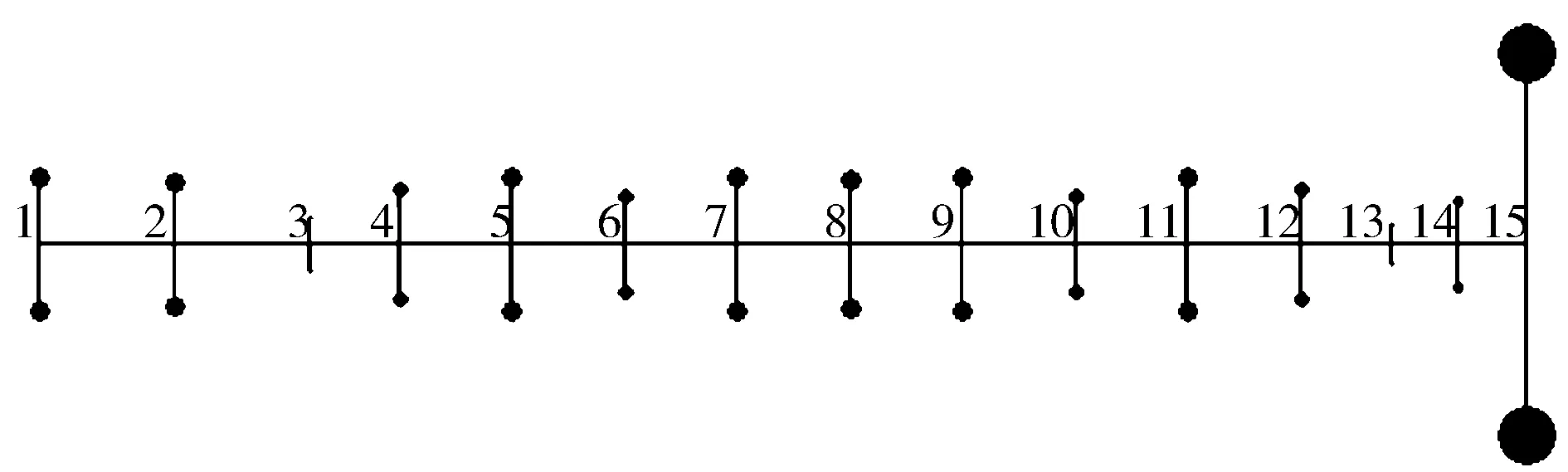
图2 当量曲轴系简化图

2.2 集中质量模型刚度、惯量的获取

以往的工程实际分析过程通常使用经验公式计算或是采用单一的有限元分析得到计算结果，都缺乏对惯量和刚度参数的校核验证，这将直接影响曲轴自由扭振的计算结果。

2.2.1 转动惯量

刚体对转动轴的转动惯量的一般表达式为

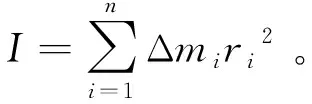
(3)

式中：Δmi为刚体上某一质量点的质量；ri为该质点对转动轴的惯性半径。

对于较复杂模型的转动惯量，如曲柄臂，很难采用上式进行理论计算。曲柄臂部件的参数可利用三维建模软件直接读取其惯量参数，操作方便并且具有较高的精度，所以本研究的惯量均由三维软件计算得到，且不再进行惯量的校核。

2.2.2 扭转刚度

曲柄由于结构比较复杂，刚度计算十分繁琐，所以是整个曲轴系刚度计算的重点和难点，在设计阶段一般使用经验公式进行计算。但是不同形状的曲柄在扭矩的作用下会有不同变形，即使同一种曲柄，轴承间隙不同，变形也不同，使得经验公式的精度难以保证。

中国船检局曲柄刚度公式[12]：

(4)

式中：Lj，Lw，Lc分别为主轴颈、曲柄臂、曲柄销的长度；Dj，dj分别为主轴颈的外径和内径；Dc，dc分别为曲柄销的内径和外径；R为曲柄销的回转中心半径；b为曲柄臂的宽度。国内外许多文献[8-10]都提到了采用有限元法计算曲柄或半拐的扭转刚度，通过有限元法计算半拐刚度，可以充分考虑到模型表面的几何特征以及各部分结构之间的弹性变形和阻尼的影响，但有限元法的计算精度与模型的简化、约束有关，同时计算曲柄臂扭转刚度时扭转中心选取也会影响计算结果，因此计算得到的扭转刚度是否准确，需要进一步评估和校正。

本研究采用基于扭转中心的有限元计算方法，使用ANSYS工具创建半拐三维模型(包含半个主轴颈、半个曲柄销、一个曲柄臂结构)并进行适当简化处理。如图3a所示，在主轴颈端面施加全约束，曲柄销端面施加以主轴颈轴线为轴心的扭矩，并对回转中心处(曲柄销下端)的网格进行加密，提取角位移结果，计算出曲柄臂的刚度。网格精度和有限元模型都会对计算结果产生影响，特别是扭转中心的选取，应根据曲柄臂实际的工作过程进行选取。根据有限元计算结果，将曲柄销端面最小变形处定义为扭转中心，以此来计算曲柄臂的扭转刚度(见图3b)。

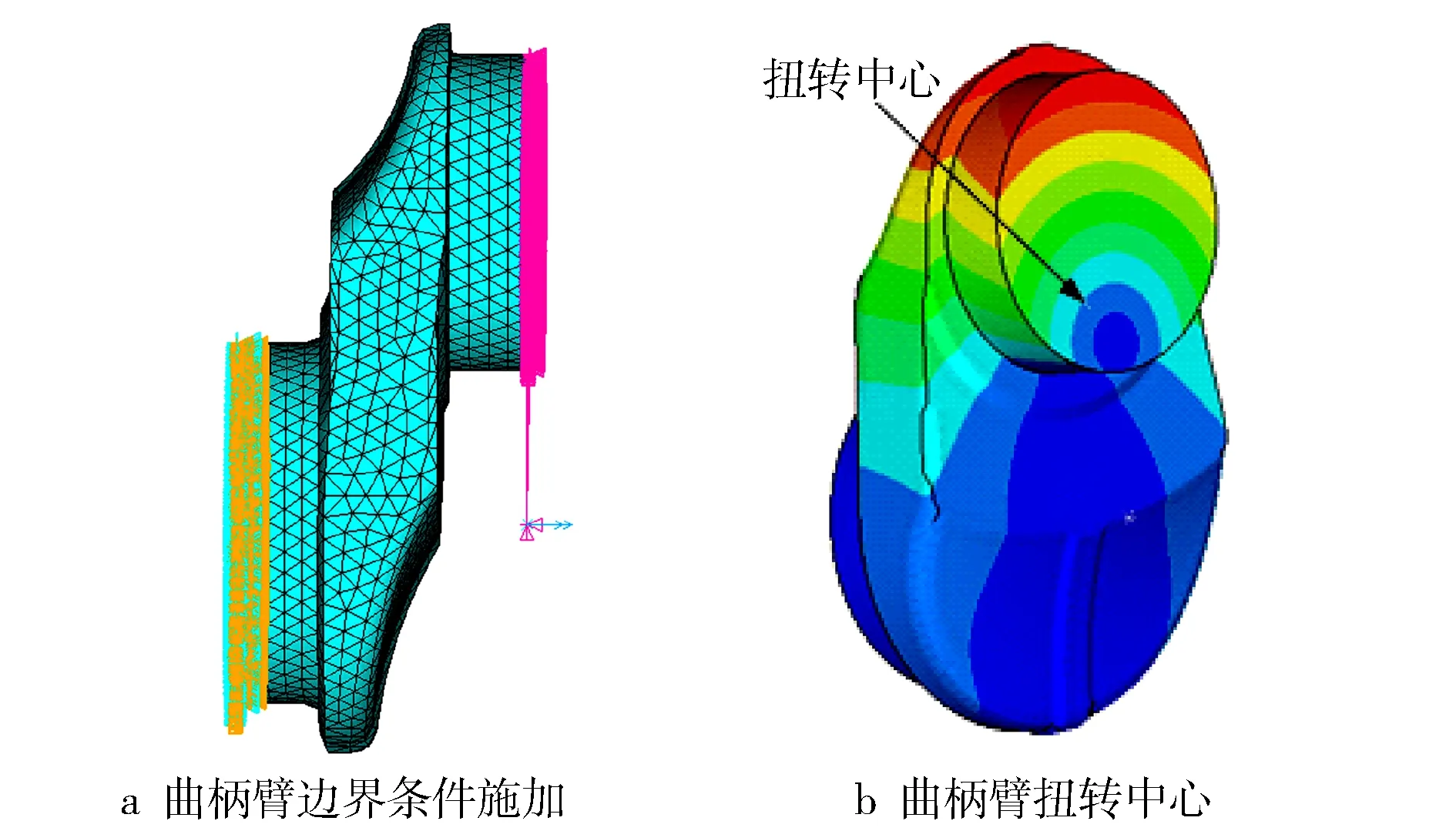
图3 曲柄臂扭转刚度计算有限元模型

有的研究把主轴颈轴线作为扭转中心，导致计算结果出现偏差。在以往的工程实践中，往往直接将有限元计算结果作为集中质量模型的输入，缺乏相应的校核验证环节，没有验证对一维模型置信度的影响，而刚度又是搭建集中质量模型的关键，需要进行相应的校核验证环节。

AVL-Excite软件自带的轴系分析程序Autoshaft能对曲轴的惯量和刚度进行计算，其曲柄臂扭转刚度的计算方法与本研究相同，均是基于扭转中心求解，但其模型的设置和自动简化会带来更多的偏差。

工程上较多应用非扭转中心的有限元法计算曲柄臂扭转刚度，由于这种算法未能反映实际的扭转中心，其计算结果与实际曲轴的扭转刚度存在着一定的差异。

分别采用经验公式法(中国船级社推荐公式)、非扭转中心法、AUTOSHAFT程序和扭转中心法计算半拐刚度数据并进行汇总对比，具体数据见表1。由表1数据可知，采用不同方法计算的半拐刚度值具有较大的差异，相比较于扭转中心法计算的刚度值，非扭转中心法计算出的刚度值比其低约8%，而AUTOSHAFT的值比其高约8%。可见，即使均采取有限元计算，不同方法计算出的扭转刚度也具有一定的偏差，这就需要对刚度数据进行评估，由此提出采用多级模态校核的方法对刚度数据进行校核验证。经验公式计算的刚度值与扭转中心法的刚度值差异较大，约20%，其结果存疑。

由于扭转中心法计算扭转刚度过程中考虑了曲柄臂的变形、网格尺寸以及扭转中心等因素，理论上更合理，且经过多级模态的校核对比，基于扭转中心法的刚度数据具有较高的精度，所以本课题组后续4缸机的扭振计算以此数据作为集中质量模型的刚度。

表1 不同方法半拐刚度对比

2.3 集中质量模型精度验证

为确保基于扭转中心法刚度数据的一维集中质量模型能够满足后续强迫振动的计算精度要求，本研究提出采用多级模态对比来验证其置信度。根据课题组以前的工作，已经验证了采用三维有限元计算方法能够很好地与实际相对应，所以本研究将三维模态作为验证的基准。利用ANSYS软件对整个曲轴进行三维模态分析，并与一维模态进行对比验证，以验证搭建的一维集中质量模型的准确性，提升置信度。

一般来说，引起发动机共振的主要是较低阶次频率，在进行轴系模态分析时，曲轴的低阶模态才对曲轴的振动分析具有重要的参考意义，因此较为关注系统低阶的固有频率。分别建立光轴、带内轮毂、带减振器的曲轴模型，对比一维模态和三维模态的固有频率和振型，可以快速判断集总参数模型的合理性。如果两种模型等效，则说明所搭建的一维集中质量模型具有较高的置信度，同时也能间接说明曲轴扭转刚度计算相对准确。

为了更好地说明校核验证环节的必要性，本研究选取两组一维仿真模态与三维模态进行对比，其中三维模态为有限元计算后提取的一阶扭转模态。一组是本课题组进行的校核仿真模型，基于扭转中心法计算扭转刚度，并且经过多级模态校核的集中质量模型(校核方案)；另一组是以工程上常用流程进行的原始简易快速有限元方案模型，未考虑扭转中心的变化对刚度的影响，同时也未经过多级模态对比的集中质量模型(简易方案)。曲轴光轴、曲轴带轮毂、曲轴带减振器对比结果分别见图4至图6。

图4 曲轴光轴扭振模型一阶扭转模态振型对比

图5 曲轴带轮毂扭振模型一阶扭转模态振型对比

图6 曲轴带减振器扭振模型一阶扭转模态振型对比

模态分析结果表明，校核方案的一维扭转模态与三维扭转模态固有频率基本相近，最大相对误差为3.5%，且带减振器模型的一维模态固有频率几乎与三维模态的相等，足以表明所建立的集中质量模型具有相当高的精度，同时也间接说明基于扭转中心法计算的扭转刚度准确合理；简易方案模型光轴和曲轴带减振器模型的一维模态精度尚可，而曲轴带轮毂模型精度与三维模型相比差异较大，达到了13.1%，已不能满足工程计算的要求。这也是采用光轴、带轮毂、带减振器三级模型进行对比的原因，若只是简单对比光轴模型，无法判断所搭建的曲轴系集中质量模型是否准确。

振型方面，校核方案模型与简易方案模型相对振幅和节点位置也存在着一定的差异。对于光轴模型，校核模型和三维模态的节点均位于第5主轴颈，而简易方案模型节点位于第5主轴颈和飞轮间的阶梯轴上。对于曲轴带轮毂模型，校核模型和三维模态的节点位于第8曲柄臂上，简易方案模型节点位于第5主轴颈上。对于曲轴带减振器模型，校核模型节点与简易方案模型的节点位置基本相近。

在上述曲轴系统集中质量模型建模过程中，通过对曲轴模型的三级模态校核已验证所搭建的校核模型合理准确，符合工程实践需求，证明所建立的曲轴系统扭振集中质量模型具有较高的置信度，可以进行后续强迫振动仿真分析。三级模态校核对比相当于在搭建仿真模型的过程中建立了一道闸门，高置信度仿真模型可以通过此闸门，而低置信度的仿真模型被驳回改进。

3 一维扭振仿真结果与模型精度的试验验证

3.1 扭振虚拟样机模型

按上述步骤在AVL-Excite Designer里建立具有较高置信度的曲轴系集中质量模型，就完成了对整个曲轴的定义，添加活塞、连杆等零部件，建立如图6所示的虚拟样机模型，便可进行相应的强迫扭转振动分析，得到曲轴各自由度角位移等仿真数据。

通过实测的强迫振动结果与仿真结果进行对比来验证前述所提出的校核验证法建立轴系集中质量模型的准确性。

图7 EXCITE缸机虚拟样机模型

3.2 试验验证

扭振分析是否准确，所提出的校核验证法是否有效，都将通过台架试验来最终验证。在发动机台架上进行扭振试验，数据采集系统和分析软件为ANZT10扭振测试仪及其配套软件。把发动机布置在测功机上，确定发动机状态良好后，安装扭振测试设备。扭振设备由三部分组成：角度编码器(200BZ-05EG10)、数采系统(ANZT0第六代单双通道扭振测试仪)和笔记本电脑(分析软件)。

测试工况为发动机转速在120 s内从1 000 r/min均匀加速到5 500 r/min，测得曲轴前端扭振的角位移随转速变化的曲线。在曲轴前端安装减振器样件，2谐次在低转速时主要受滚振影响，在高转速时由于谐次较低难以与曲轴固有频率发生共振，对曲轴危害较小，所以主要对4，6，8，10这几个主谐次的试验值与仿真值进行对比，验证前述校核验证方法建立仿真模型的有效性以及准确性，结果见图8。

结果表明：校核后的一维模型仿真结果和台架试验有较好的一致性，各谐次变化规律基本一致，扭振峰值转速和幅值都较为吻合，各谐次仿真振幅均略低于实测值，与台架试验存在着其他外部噪声激励有关，这点可以从4、6谐次仿真值存在着0振幅点而实测值不存在0振幅点可以看出。与简易方案的模型仿真结果比较，校核方案模型仿真值与实测值之间的偏差小很多，具有很好的置信度，说明提出的多级校核验证方法行之有效。

图8 曲轴前端各阶次角位移结果

工程上常采用的简易方案模型的一维仿真数据与实测值扭振变化规律偏差较大，各谐次共振转速与实测的共振转速基本相差300 r/min，这也说明简易方案的集中质量模型与实际不符；扭振振幅方面，4、6谐次的振幅略高于实测值，而8、10谐次略低于实测值，没有出现由于存在着外部噪声激励导致实测值普遍偏高于仿真值的规律，说明仿真模型的置信度不够。除此之外，相对于实测振幅曲线，未经校核的振幅曲线整体发生左移，这说明相对于实际曲轴结构，简易方案模型的固有频率偏低，这也能与前文模态对比时的数据相呼应。

4 结论

a) 采用集总参数法的虚拟样机模型仿真可以较好地预测发动机实际工作扭振状况，预测准确程度取决于集中质量模型的准确性；

b) 轴系一维模型的精度取决于模型惯量、刚度参数的准确性，在曲轴扭振分析计算中需要对轴系当量模型参数进行验证及评估；

c) 验证扭振模型能否满足后续强迫振动的计算精度要求，即保证一维集中质量模型计算精度，可以通过一维三维模态对比来判断，以此来提升一维集中质量模型的置信度，建议采取光轴、带轮毂、带减振器三种方式的一维三维模态对比；

d) 通过此方法对轴系进行扭振分析，在台架试验前就可以预估其准确度，不仅可以缩短计算分析时间，同时也能得到较为准确的结果，可靠性好，经工程应用验证，较为快速有效。