小型排涝泵站机电设备的维护优化方案
谢粤荣
(沙坪河水利枢纽管理中心,广东 鹤山 529700)
1 概 述
水泵的预期使用寿命很长,特别是较老的型号[1]。据统计数据,大多数水泵都能使用20年左右,然后才开始出现故障[2]。水泵的运行方式是把水抽到蓄水池里,再根据需要从蓄水池中排出[3]。随着时间的推移,一些型号的水泵有可能停产,因此水泵之间没有统一的效率标准,这给研究人员带来困扰。一般在泵站的输水线都安装有变频驱动(VFD),可以控制抽水的速度。维修人员通过几类参数来测试泵的缺陷,如电阻温度装置(RTD)进行振动测试、油液分析,同时运行的水泵不超过2~3个,这样可以对未工作的水泵进行维护[4]。泵站维护和更换计划为何时应执行特定类型的预防维护操作提供了依据[5]。
一些泵站在修复多年的旧设备上花费了过高的成本,总修理维护费用之和比更换新设备的成本要高得多。本研究的主要目标是开发一个数学模型,用来优化泵站设备的维修和更换方案。除了获得最优调度方案外,还提出一个基于Excel的决策系统,决策者可以通过更改成本和故障参数来解决系统问题。
2 工程概况
本文以某小型排涝站为研究对象。排涝站2008年建成并投入使用,工程等级为Ⅳ等,泵站按10年一遇24 h暴雨1 d排干的农排标准设计,泵机组共安装3台卧式电机,单机容量120 kW,总装机容量360 kW,设计总流量6 m3/s。泵站建成后,随着时间的推移,一些泵出现故障。本文以该泵站作为案例,进行以下研究。
3 成本构成
3.1 维护成本
计算泵站系统维护需要考虑以下几个因素,即泵站部件的可靠性、维护成本和部件的有效使用年限。在对部件进行维修后,该部件的有效使用年限将延长。但会导致在下一个周期j开始计算时降低了部件i的真实使用年限。式(1)说明了维护后有效年限与周期结束时有效年限间的关系。
Xi,j+1=αi×Yi,j
(1)
其中:αi为改进系数;Yi,j为i组件j周期结束时有效年限;Xi,j+1为i组件维护后有效年限。
3.2 更换成本
更换操作是将组件的有效使用年限恢复到零,使系统表现得像新的一样,并且系统的故障率也回到零。系统的更换成本与维护成本相似,表示目标函数中的重置成本,该成本是在周期j结束时发生的,更换成本等于组件i的初始价格。进行更换对系统不造成影响,系统继续以一定的速度老化。部件i的有效年限和故障率将继续增加,并且在给定周期j结束时,系统将完全失效。式(2)给出了进行部件更换对系统造成的影响。
Xi,j+1=0
(2)
3.3 时间流逝造成的影响
本节不对泵站系统进行任何更改(维护或更换)。人为因素对系统没有影响,因此系统继续随着时间以一定的速度老化。部件i的有效寿命和故障率将继续增加,到给定的周期j结束时,系统将完全失效。以下公式反映了时间流逝对系统的影响:
Xi,j+1=Yi,j
(3)
(4)
3.4 故障成本
随着时间的推移,泵站系统中的组件将持续出现故障。维护和更换只会延迟组件的故障率,或者将故障率重置回零。无论系统在何时出现故障,都会有与其故障相关的成本。在目标函数中定义的故障成本考虑了系统在任何时间都可能发生故障。该意外故障成本可以通过先前故障成本的平均值来确定。
3.5 固定停工成本
对于串联配置的系统,将有固定的停机成本。如果一个组件发生故障,则必须关闭整个系统以维护或更换该特定组件。收入损失或其他相关因素而关闭该系统产生的费用必须包括在总体目标函数中。
4 基于Excel的决策系统
基于电子表格的决策系统是通过以下几个阶段建立的。这需要了解VBA(应用程序VB语言)、LINGO(线性规划软件)和Excel三者之间的相互作用。为了创建决策系统,首先从一个基本的Excel表开始,添加用户表单和控件来导航该程序。用户界面的背后是嵌入在每个工作表和用户表单中的VBA代码层,使得电子表格与进行数学计算的LINGO软件互相联系。为达到该目的,LINGO代码中使用了一个对象链接和嵌入(OLE)的本机函数。这个OLE函数使LINGO能够从Excel文件中接收数据(软件输入过程),并向Excel输出最佳解决方案。在LINGO中,编码语言用于将数学模型转换成可执行代码。
在Excel表单中,决策者输入关于组件数量、规划范围等信息,接下来进入到故障参数页面,该页面有所有故障参数的选项。下一步进入成本输入界面,在此输入与系统相关的所有成本,在该界面Excel通过LINGO来解决问题,并显示一个输出界面和一个报告选项界面。共有4种不同的报告选项,即查看计划、稳定性与时间关系、成本与时间关系和总成本。在整个过程中,LINGO在后台不断收集信息,并将结果输入到表单界面。
5 模型应用
本研究的重点是3个独立的部件,电机、泵和球阀。为了使研究周期足够包括所有组件的更换周期,并且不会因为太长而影响准确性,故选择60 a作为规划周期。为了测试系统的稳定性,还对设备和其他变量的相关成本进行了分析。
5.1 维护和更换成本
泵的维护和更换成本是系统所需要确定的第一类成本。根据记录,大约每15年对泵进行一次全面翻新。翻新包括动态平衡测试和更换轴套、轴承和耐磨环。表1为与这些更换项目相关的成本。

表1 更换项目相关的成本
机械密封的维护周期大概是10年一次。为了保持一致,将所有维护周期标准化,选择9年一次的电机翻新周期作为标准。为了计算泵维护的成本,将泵的总翻新成本乘以(9/15)。同样,机械密封的成本乘以(9/10)。动平衡测试和灌注室密封更换每5年进行一次,费用为700元。这些成本的总和为泵的维护成本,见式(5)。而用类似容量的新泵替换该泵的成本约为18万元。
维护费用泵=13 800×(9/15)+10 000×(9/10)+700×(9/5)=18 540(元)
(5)
泵机组的电机是卧式电机。维护成本均按照电机的9年翻新期进行标准化。在此期间,所有轴承和油封都要更换,绕组也要清洗、重新浸泡和烘烤,总成本约为18 000元。与泵相似,该电机的机械密封大约每10年更换一次,费用约为5 000元。此外,每年需要对电机进行振动测试,每台成本为750元。式(6)给出了电机的总维护成本。即替换类似的电气发动机大约要花费10万元。
维护费用发动机=18 000×(9/9)+5 000×(9/10)+750×(9/1)=29 250(元)
(6)
与泵和电机不同,球阀不需要维护。组成阀门的单个零件使用寿命与整个阀门的使用寿命大致相同。更换球阀的成本大约为28 000元。
5.2 故障成本
在许多系统中,故障设备的更换除了新设备的费用之外,还会产生其他费用。这些费用包括生产产值损失、清理成本和许多其他不可预见的成本。故障成本通常很难估计,在该泵站案例中,故障成本以3个部件的更换成本来计算。
5.3 故障数据
在先前的研究中,通常将设备故障数据与威布尔分布相关联,几乎所有的设备故障都遵循这种特定的分布。使用威布尔曲线来表示设备故障需要估计两个参数,即特征寿命(规模)和形状参数。为了估计这些参数,首先确定每个组件的平均故障时间(MTTF)和该故障的标准偏差。表2为每个组件的MTTF和标准偏差的初始值。

表2 每个组件平均故障时间和该故障标准偏差时间
通过表2给出的数据,利用式(7)和式(8)计算每个组件的威布尔标度θ和形状参数β。求解后得到的结果见表3。

表3 每个组件的威布尔标度θ和形状参数β
(7)
(8)
威布尔分布可以代表不可配对系统,然而它没有准确地描述可修复设备的分布。非齐次泊松变化(NHPP)是用于可修复系统威布尔分布的变换。通过式(9)和式(10)可以将威布尔标度和形状参数转换成NHPP参数。
(9)
βNHPP=β-1
(10)
转换后的NHPP参数见表4。

表4 NHPP参数
泵站的高稳定性至关重要。为了在60 a的规划周期内保证泵站具有99%的稳定性,必须实现每年高达0.999 833的稳定性。式(11)给出的可靠性(RR)是在模型应用中使用的稳定性约束。
(11)
上述计算结果表明,泵机组作为一个整体,必须在规划范围内保持0.83以上的稳定性。每个泵单元的配置是串联的,因此:
R发动机×R泵×R球阀≥RR
(12)
5.4 其他假设
每当泵机组被迫关闭时,会产生系统关闭成本。由于组件是串联的,要关闭其中一个,其余两个也必须关闭。在这种情况下,最好在系统已经关闭的情况下,对所有3个组件进行预防性维护,而不是关闭3次线路。假设停机成本相对较高,为50 000元。
最后一个假设是每次维护操作对部件有效寿命的影响。维护成本作为维护操作对组件的影响指标,通过式(13)表达如下:
(13)
根据这个公式,维护系数α越大,执行维护的成本越高,对组件寿命的影响就越大。表5给出每个组件的α值。

表5 组件的维护系数值
6 运行结果
该模型的运行结果是建议在24 a更换电机和球阀,并对泵进行翻新。图1给出泵机组的最佳预防性维护计划,按照此预防性维护计划,预计总成本为1 239 088.12元。该金额是在60 a规划期内维护所有3个组件的预期成本。

图1 最佳维护计划
除了给出维护时间表,决策系统还给出关于3个组件的其他信息。稳定性与时间的关系形成一个表格,显示出每个时期每个组件的稳定性。图2给出了在规划期60 a,系统作为一个整体的稳定性。

图2 每年总体可靠性
从图2中可以看出,在整个规划周期中,系统的整体稳定性从未低于83%的稳定性要求。维护时间表给出的第一轮预防性维护在第24年执行,第二轮在第39年执行,稳定性在第一轮维护中下降的更明显,因为电机和球阀都在这一时期被更换,而在第39年只有球阀被更换,故第二轮维护后系统的的稳定性没有明显下降。在规划期60 a的末尾期,稳定性徘徊在83%以上。成本与时间的关系显示了3个组件在60 a期间的累计成本和每个期间的成本。
在第24年和第39年,按照时间表会有两笔大额支出。这为决策者进行提前财政预算提供了依据。见图3和图4。
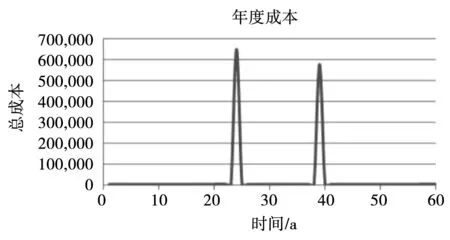
图3 年度成本

图4 年度累计成本
图5给出了累计成本与系统稳定性的联系。由图5可知,随着系统稳定性的降低,成本将会增加。成本的大幅下降在90%~93%的稳定性之间。这揭示了另一种规律:当系统接近90%以下稳定性范围时,建议进行重大预防性维护检修。
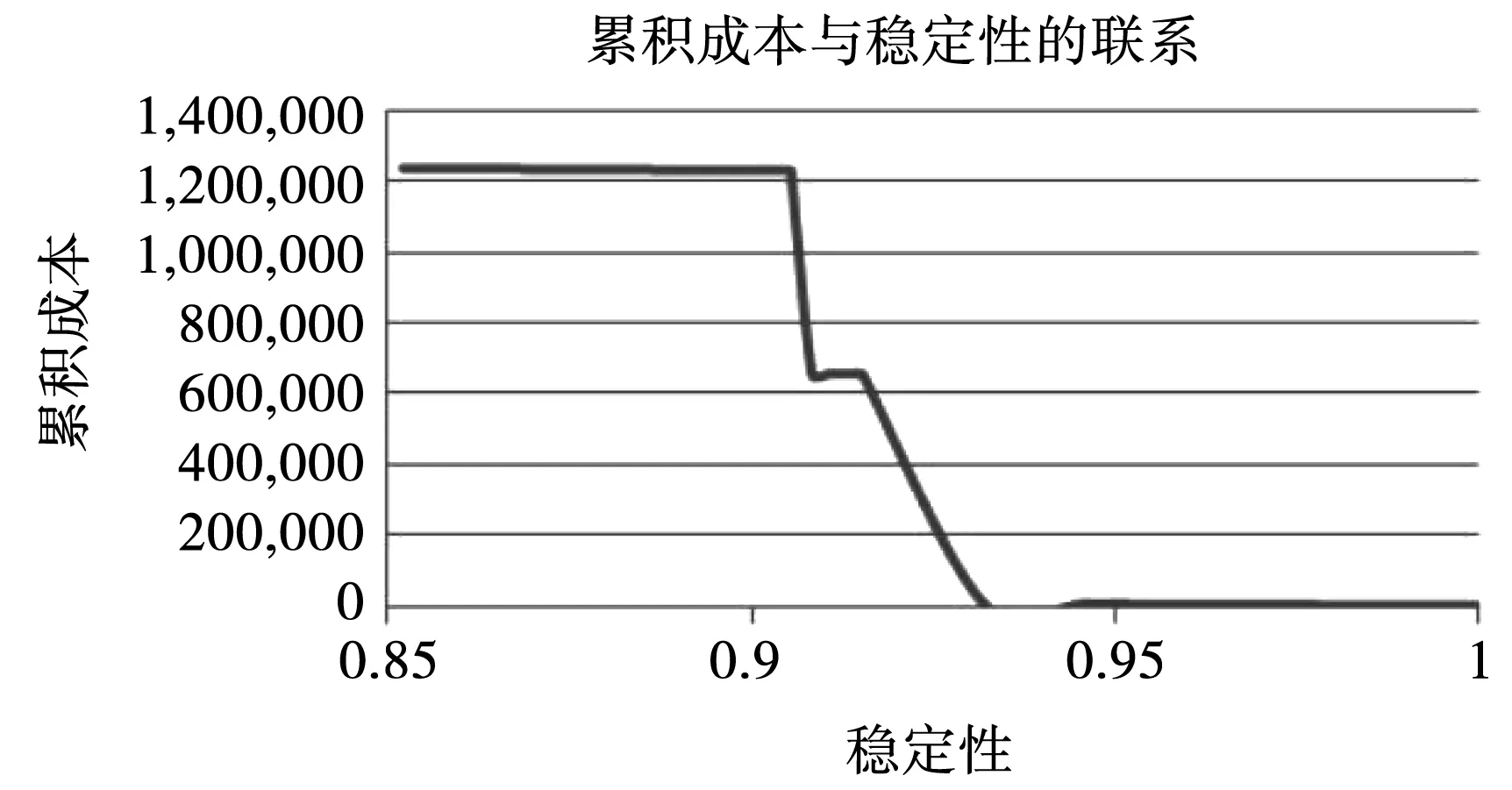
图5 累计成本与系统稳定性的联系
7 结 论
本文建立了包括维护成本、更换成本、时间流逝成本、故障成本、固定停工成本的规划模型,通过基于Excel的决策支持系统和LINGO软件进行求解,并在沙坪河排涝站泵机组中进行了实例验证,最终确定了最佳的预防性维护计划:建议在使用24 a后更换电机和球阀,第39年再次更换球阀。因为泵的故障率很低,故在60 a规划期运行中更换泵是不经济的。同时还分析了规划期间内系统作为一个整体的稳定性,年度成本、年度累计成本与时间之间的关系,并将累计成本与稳定性联系起来。该研究能为泵站的长期维护和更换提供指导方案和依据。

