基于广义随机空间的护面块体稳定性概率分析
张宝华,刘俊涛,蒋学炼,张 笑*
(1.交通运输部天津水运工程科学研究所,天津 300456;2.天津水运工程勘察设计院有限公司,天津 300456;3.天津城建大学 天津市软土特性与工程环境重点实验室,天津 300384)
护面块体是防波堤的主要消浪构件,其稳定性决定了堤身的尺度和安全。李炎保等[1]基于世界各国200余例防波堤典型损坏案例的统计分析指出,护面块体散乱占斜坡式防波堤受灾总数的59.2%,而破损的直立式防波堤无一例外伴随着消浪棱体散乱和消浪棱体损坏现象。周枝荣等[2]通过三维稳定试验发现,由于破波流对底部块体的冲击,浅水非标准段块体的稳定重量需增加到设计值的2.0~2.3倍。李东洋等[3]采用OpenFOAM三维数值波浪水槽模拟了不规则波越浪对堤后护面层的冲击效应。Lee等[4]构建了基于和谐搜索算法(harmony search algorithm)的神经网络模型HS-ANN,用于预测斜坡堤护面块体的稳定数。钟雄华等[5]、江超等[6]采用模型试验分别探讨了不同安放方式对扭王字块体、透空式四面体和六面体、四角锥体的空隙率和稳定性的影响。上述研究表明,护面块体的失稳是一个随机过程,其中设计参数中存在的不确定性是内在诱因之一。为此,本文引入广义随机空间可靠度计算方法对护面块体的稳定性进行概率分析,以阐明设计公式和设计参数中的不确定性对块体稳定的影响。
1 广义随机空间可靠度计算方法
结构可靠度的计算方法有三个水准:半经验半概率法(水准I)、近似概率法(水准II)、全概率法(水准III)。从工程应用角度看,半经验半概率法精度较低不能满足实际需要,全概率法受随机变量联合分布研究水平的限制很难推广,只有近似概率法能够满足工程需要的精度且计算简便,是目前规范标准推荐使用的方法。常用的近似概率法有一次二阶矩法、二次二阶矩法等[7-8],由于这些方法采用的是正交直角坐标系(笛卡儿空间),故对于相关的随机变量,需要转化为不相关的随机变量才能进行计算。本文将设计变量定义于非正交坐标系,在广义随机空间内进行可靠度计算,无需将相关变量正交化,计算更为直接[9]。以下简要介绍这一算法。
设随机变量X1,X2,…,Xn构成一个n维广义随机空间,Xi与Xj的相关系数为ρXi Xj。在广义随机空间中,随机变量间的相关系数为各坐标轴夹角的余弦,如式(1)所示。当变量间的相关系数均为0时,广义随机空间即为笛卡儿正交空间。
θXi Xj=arccos(ρXi Xj)
(1)
图1展示了可靠指标β的几何意义,即坐标系原点至极限状态曲面间的最短距离。这一最短距离可通过搜索极限状态曲面的切平面法线得到:

图1 广义随机空间可靠指标和验算点示意Fig.1 Design point and reliability index in the generalized random space
首先,将随机变量Xi(i=1,2,…,n)转换为标准正态分布Yi(i=1,2,…,n)
(2)
线性变换不会改变随机变量间的相关关系。转换后Yi的均值和标准差分别为μYi=0,σYi=1。将式(2)代入结构的功能函数
Z=GY(Y1,Y2,…,Yn)=0
(3)
假设功能函数连续,且对于所有随机变量其偏导数均存在,则极限状态曲面上任一点处的切平面法线方向表示为
(4)
以两个随机变量情形为例(图1),当极限状态曲面上P点的切平面法线通过坐标原点O时,OP距离最短(即可靠指标β),P点为极限状态临界点,称为验算点。
由式(4),P点切平面的法线方向为
(5)
(6)


(7)
根据可靠指标的几何意义,验算点P的坐标Y*应满足
(8)
极限状态方程可写为
(9)

此外,由于可靠度计算理论构建于正态空间中,对于非正态的随机变量,需要通过等概率变换、当量正态化、Rosenblatt变换等方法转化为正态随机变量,具体操作详见文献[10]。
采用文献[11]中的算例检验广义随机空间可靠度计算方法的有效性。算例条件为:结构功能函数Z=g(X1,X2)=X1X2-130,随机变量X1和X2服从正态分布,均值和标准差分别为μX1=38.0,σX1=3.80,μX2=7.0,σX2=1.05,相关系数ρ12分别取-0.9、-0.2、0.0、0.2、0.9。验算点和可靠指标的计算结果列于表1。可以看出,广义随机空间可靠度计算结果与改进一次二阶矩法及原文献一致,相对于改进一次二阶矩法,广义随机空间法在处理变量相关方面更为便捷。

表1 可靠度计算方法验证Tab.1 Verification of reliability calculation method
2 护面块体稳定性公式比较
护面块体的稳定性验算常采用Hudson公式和Van de Meer公式[12],以功能函数的形式写出
Hudson公式
G1(X)=Y1ΔDn50(KDcotα)1/3-Hs
(10)
Van der Meer公式(卷破波)
(11)
Van der Meer公式(崩破波)
(12)


表2 无量纲稳定系数KD[13]Tab.2 Non-dimensional stability coefficient KD

表3 Hudson公式和Van de Meer公式破坏程度的对应关系[13]Tab.3 The corresponding damage levels between Hudson formula and Van de Meer formula
为了比较上述两套护面块体稳定性验算公式在概率设计方面的优劣,采用可靠度影响系数的平方作为敏感性因子衡量公式中各随机设计参数对结构可靠度的贡献
(13)
同时,采用相对变动因子来衡量各设计参数本身的随机性对结构可靠度的影响程度
(14)
上述两套公式中的设计参数的概率分布和相关关系分别见表4[14]和表5[15]。

表4 设计参数的概率分布Tab.4 The probability distribution of design parameters

表5 设计参数的相关关系Tab.5 Correlation of design parameters
基于第一节中的广义随机空间可靠度方法和表4~表5的设计参数概率特性及相关关系,计算得到不同工况下的敏感性因子和相对变动因子。各工况的计算结果表现出一致的规律。此处以一典型工况的敏感性分析结果(表6和表7)为例进行说明:随机抛放粗糙块石,破坏程度DL=0%~5%、KD=4、S=2,设计参数独立不相关。表6显示,Hudson公式本身随机性的敏感性因子SFY1=67.42%,相对变动因子RC=1.75,表明公式本身的不确定性对可靠指标的影响最大,考虑因素过少。此外,与波浪要素相关的设计参数HS和FHs的敏感性因子和相对变动因子分别为19.67%和9.89%,敏感度较高。其余变量的敏感性因子和相对变动因子均很小,说明其随机性对可靠度贡献很小,在设计中可取定值。表7显示,Van de Meer公式的敏感性结果与Hudson公式差别很大,敏感性最强的设计参数均是与波浪要素相关的变量(Hs、FHs、Hs/Lz),公式本身的敏感性因子和相对变动因子分别为SFY2=10.85%、RC=1.06,相对较小。其它变量的敏感程度很小,在设计中可取定值。

表6 敏感性分析(Hudson公式)Tab.6 Sensitivity analysis of Hudson formula

表7 敏感性分析(Van der Meer公式)Tab.7 Sensitivity analysis of Van de Meer formula
总体来说,与Hudson公式比较,Van de Meer公式纳入了更多的重要影响因素,如波浪周期、波浪历时、结构渗透性等,其不确定性主要来自于客观的波浪条件,公式本身的随机性并不显著。此外,以上研究表明,可靠度分析不仅可用于求取结构的可靠指标和失效概率,还可用于比较同类型设计公式的优劣,衡量设计变量的重要程度,从而指导技术工作的重点。
3 护面块体稳定性概率分析
以下采用Van de Meer公式进行护面块体稳定性的概率分析,各设计参数的概率分布和相关关系见表4~表5,各种情况的计算结果见图2。图2-a给定结构设计使用年限L=50 a,得到不同破坏水平下的结构失效概率-名义直径曲线。结果显示,当选定使用期限和失效概率时,破坏程度随名义直径的增大而减小,意味着在工程设计中若选择较小的护面块石粒径,初始建造费用将下降,但会增加后期的维护费用,需要从全生命周期费用角度进行平衡。图2-b给定破坏程度S=2,得到不同使用期限下的结构失效概率-名义直径曲线。结果显示,当选定破坏程度和失效概率时,使用期限的延长对应着护面块石粒径的增大,意味着在工程设计中应基于全生命周期费用效益比选择合理的使用期限。图2-c给定名义直径Dn50=1.0 m(标准差0.03),得到不同使用期限下的结构失效概率-破坏水平曲线。结果显示,当选定名义直径和失效概率时,使用期限越长,破坏程度加剧,同样意味着工程设计中应基于全生命周期费用效益比平衡使用年限和风险水平。为了探讨变量相关对失效概率的影响,图2-d给定结构设计使用年限L=50 a,得到变量独立和变量相关情况下的结构失效概率-名义直径曲线。数据表明,变量相关对结构的失效概率有一定的影响。例如S=6时,变量相关较变量不相关的失效概率高出约12%,由于防波堤工程往往位于恶劣的工作环境,这可能意味着巨大的风险损失。目前工程设计对此考虑很少,可能低估失效概率和风险损失,应加强研究,尽可能准确地估计和引入设计变量相关性。


图2表明,除设计波高外,使用期限、名义直径、容许破坏水平等均会影响护面块体的失稳概率,同时,这4个变量也决定了工程投资中的初始建造费用和后期维护费用的相对占比。从工程经济角度来看,目前设计中选用确定的使用期限并不完全合理。为此,由风险分析的概念Risk=f(失效概率,失效后果),可建立基于可靠度的全生命周期风险评估方法,将结构的失效概率与设计变量、失效后果联立获得优化的设计方案。
以图2-b中S=2、L=100 a的情况为例,失效损失为失效概率和破坏程度的函数,如式(15)所示,计算得到名义直径与失效损失的关系曲线(图3),其中失效损失以Dn50=1.0 m的对应值为基础标准化。图3显示,本工况的最优名义直径在Dn50=1.0 m附近。
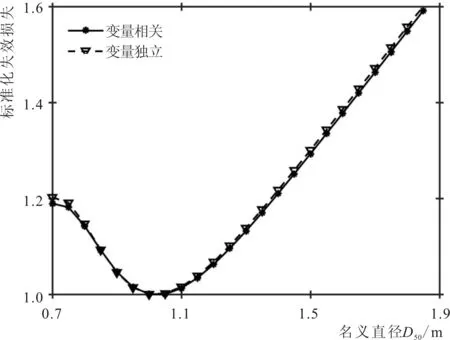
图3 名义直径与失效损失关系曲线(L=100 a)Fig.3 Relationship between nominal diameter and normalized failure cost (L=100 a)
Rexp=Pf·Ed(S)
(15)
式中:Rexp为失效损失的期望经济价值,Ed(S)为与破坏程度S对应的失效后果经济价值,本文假定失效后果的经济价值与损失程度成正比,即Ed(S)=CdS,其中Cd为经济损失系数。
4 结语
(1)广义随机空间可靠度计算方法属于近似概率法,其随机变量定义于非正交坐标轴的坐标系中,进行可靠度计算时无需将相关的随机变量正交化,相对于一次二阶矩法、二次二阶矩法等常用的水准II方法更为便捷。
(2)结构可靠度分析可用于比较同类设计公式的优劣和衡量设计参数的相对重要性。Hudson公式的不确定性主要来自公式本身的随机性,而Van de Meer公式的不确定性主要来自于客观的波浪条件,公式本身的随机性并不显著。
(3)概率分析结果表明,护面块体稳定性的主要影响参数为使用期限、名义直径、容许破坏水平,变量相关性对结构的可靠度有一定的影响,忽视相关性可能会低估失效概率和风险损失。可建立基于可靠度的全生命周期风险评估方法,通过设计变量的不同组合获得最优设计方案。

