浅谈含弹簧能量信息给予问题的解题策略
■窦传家
在我们遇到的含弹簧问题中,与弹簧相接触的物体运动时,弹簧被压缩或被拉伸,弹簧的弹力发生变化,弹簧的弹力对物体做功是变力做功,弹簧储存的弹性势能也随之发生变化。下面根据这类问题信息给予的不同特点,探讨相应的解题策略,希望对同学们有所启发。
一、两个状态下弹簧的伸长量(压缩量)相等
弹簧发生形变时,弹簧储存弹性势能。同一弹簧,若在两个状态下的伸长量(压缩量)相等,则说明弹簧储存的弹性势能相等。
例1 如图1所示,在轻质弹簧的下端悬挂一个质量为m的小球A,将小球A从弹簧原长位置由静止释放,小球A能够下降的最大高度为h。若将小球A换为质量为3m的小球B,仍从弹簧原长位置由静止释放(重力加速度为g,不计空气阻力),则小球B下降高度h时的速度为( )。
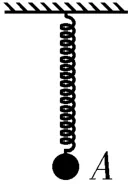
图1
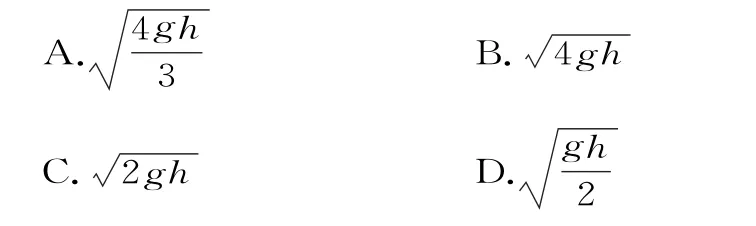


答案:A相等,且弹性势能的大小关系也不确定。
二、两个状态下弹簧的压缩量与伸长量相等
弹簧发生形变时,弹簧储存弹性势能。同一弹簧,若在两个状态下的伸长量与压缩量相等,则说明弹簧储存的弹性势能相等。
例2 如图2所示,质量均为m的A、B两物体用劲度系数为k的轻质弹簧拴接在一起,竖直放置在水平地面上,处于静止状态。在物体A正上方h高处有一质量也为m的小球C。将小球C由静止释放,小球C与物体A发生碰撞后立刻粘在一起,向下压缩弹簧,弹簧始终在弹性限度内,忽略空气阻力,重力加速度为g,要使物体B刚好被拉离地面,求高度h(用m、g、k表示)。
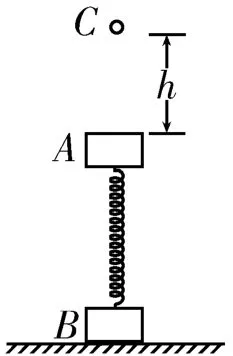
图2

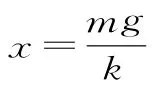

因为A、B两物体的质量均为m,物体A处于静止状态时弹簧的压缩量与物体B刚要离开地面时弹簧的伸长量相等,所以在这两个状态下弹簧储存的弹性势能相等。如果A、B两物体的质量不相等,那么物体A处于静止状态时弹簧的压缩量与物体B刚要离开地面时弹簧的伸长量就不相等,在这两个状态下弹簧储存的弹性势能也不相等。
三、两个状态下弹簧的压缩量和伸长量不相等
弹簧发生形变时,弹簧储存弹性势能。同一弹簧,若在两个状态下的伸长量与压缩量不相等,则弹簧储存的弹性势能不相等,但弹簧储存的弹性势能之差保持不变。
例3 如图3所示,质量为m1的物体A经一轻质弹簧与下方地面上质量为m2的物体B相连,弹簧的劲度系数为k,物体A、B均处于静止状态。一条不可伸长的轻绳绕过两个轻小定滑轮,一端连接物体A,另一端连接一轻质挂钩。开始时,各段绳都处于伸直状态,物体A上方的一段绳沿竖直方向。现在挂钩上挂一质量为m3的物体C并由静止释放,它恰好能使物体B离开地面但不继续上升。已知重力加速度为g。
(1)求在此过程中物体A上升的高度。
(2)求在此过程中弹簧弹性势能的增加量。
(3)若将物体C换成另一个质量为m1+m3的物体D,仍从上述初始位置由静止释放,则这次物体B刚要离开地面时,物体D的速度是多大?
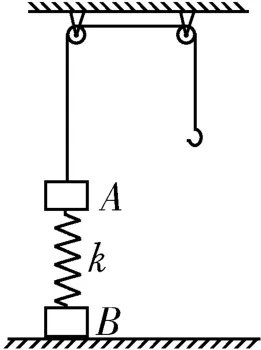
图3



物体A、B的质量不相等,弹簧最初的压缩量和物体B刚要离开地面时弹簧的伸长量不相等,在这两个状态下弹簧储存的弹性势能不相等,但是在这两个状态下弹簧储存的弹性势能之差是保持不变的。本题(3)问若是问物体B离开地面之前(之后)的某时刻,物体D的速度大小,则根据题目已有的信息是无法求解的。

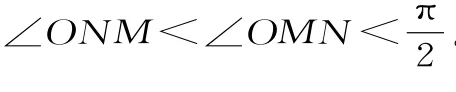
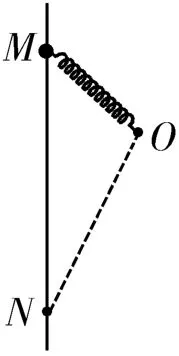
图4
A.弹力对小球先做正功后做负功
B.有两个时刻小球的加速度等于重力加速度
C.弹簧长度最短时,弹力对小球做功的功率为零
D.小球到达N点时的动能等于其在M、N两点的重力势能差
2.如图5甲所示,轻质弹簧原长为2l,将弹簧竖直放置在地面上,在其顶端将一质量为5m的物体由静止释放,当弹簧被压缩到最短时,弹簧长度为l。如图5乙所示,将该弹簧水平放置,一端固定在A点处的竖直墙壁上,另一端与物块P接触但不拴接。AB段是长度为5l的水平轨道,在B点与半径为l的光滑半圆形轨道BCD相切,半圆的直径BD竖直。物块P与轨道AB间的动摩擦因数μ=0.5。用外力推动物块P,将弹簧压缩至长度为l,然后放开物块P,它将沿轨道运动。已知重力加速度为g,物块P的质量为m。求物块P到达B点时速度的大小。
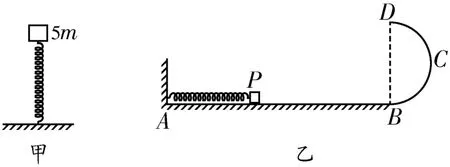
图5
3.如图6所示,质量为m1的物体A经一轻质弹簧与下方地面上质量为m2的物体B相连,弹簧的劲度系数为k,物体A、B都处于静止状态,此时弹簧的弹性势能为Ep1。一条不可伸长的轻绳绕过两个轻小定滑轮,一端连接物体A,另一端连接一轻质挂钩。开始时,各段绳都处于伸直状态,物体A上方的一段绳沿竖直方向。现在挂钩上挂一物体C并由静止释放,它恰好能使物体B离开地面但不继续上升,此时弹簧的弹性势能为Ep2。已知重力加速度为g。求物体C的质量。
参考答案:
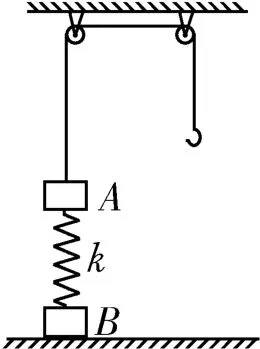
图6

