2020 年高考“三角恒等变换”问题聚焦
■何 敏 刘大鸣(特级教师)
2020年高考“三角恒等变换”主要围绕“三角函数的定义、三角函数的求值、方程组观念的应用、合理的降次和辅助角公式及与其他知识的交汇应用”等展开,彰显“整体变量观念、转化化归和数形结合”的数学素养的具体应用。
聚焦1:利用和差角公式求值

回味:解答三角函数的给值求值问题,关键是用所求角表示已知角,再对条件和三角公式进行沟通,凸显目标意识下灵活选用公式并进行计算的学科素养。

聚焦2:利用二倍角公式求值

回味:由题设条件和二倍角的余弦公式,求得cosα的值,再利用同角关系得出结果。
变式训练2:已知α为第四象限角,则( )。
A.cos2α>0 B.cos2α<0
C.sin2α>0 D.sin2α<0

聚焦3:三角恒等变换的综合问题
例3 (2020年高考北京卷)2020年3月14日是全球首个国际圆周率日(πDay)。历史上,求圆周率π的方法有多种,与中国传统数学中的“割圆术”相似,数学家阿尔·卡西的方法是:当正整数n充分大时,计算单位圆的内接正6n边形的周长和外切正6n边形(各边均与圆相切的正6n边形)的周长,将它们的算术平均数作为2π的近似值。按照阿尔·卡西的方法,π的近似值的表达方式是( )。
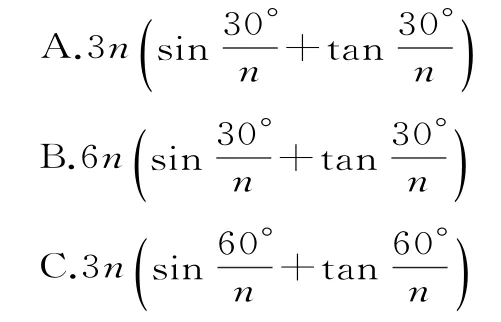

回味:理解π的近似值的意义,把握圆内接正六边形和圆外切正六边形的关系,构造直角三角形,利用边长之间的关系求解,凸显三角恒等变换的工具性和应用性。
变式训练3:已知函数f(x)=cos2x+cos2(x+α)+cos2(x+β),其中α,β为常数,且满足0≤α<β≤π。对于任意实数x,问是否存在α,β,使得f(x)是与x无关的定值。若存在,求出α,β的值;若不存在,请说明理由。


聚焦4:三角恒等变换与三角函数性质的交汇问题
例4 (2020年高考北京卷)若函数f(x)=sin(x+φ)+cosx的最大值为2,则常数φ的一个取值为____。

回味:求三角函数的最值,实质上是辅助角公式asinx+bcosx=a2+b2sin(x+θ)的应用,凸显数学运算、数学建模的学科素养。
变式训练4:已知函数f(x)=2cos2xsin2x+2,则( )。
A.f(x)的最小正周期为π,最大值为3
B.f(x)的最小正周期为π,最大值为4
C.f(x)的最小正周期为2π,最大值为3
D.f(x)的最小正周期为2π,最大值为4


