三角恒等变换中的三个小技巧
2021-06-29 07:44杜海洋
中学生数理化·高一版 2021年6期
■杜海洋
三角恒等变换是学好三角函数的基础知识,是解答三角函数问题必备的基本功。下面就三角恒等变换中的三个小技巧,举例说明,以飨读者。
一、角变换的技巧
角变换的解题思路是:观察问题中角之间的关系,把未知角分解成已知角的和、差、倍、半角,然后利用相应的公式求解。
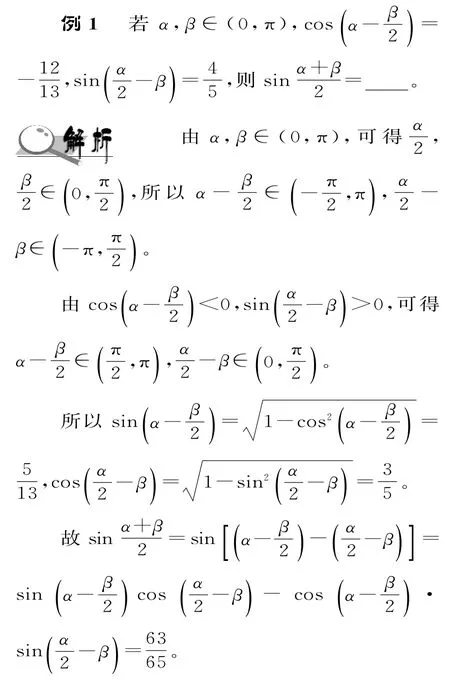

善于发现所求的角与已知条件的角的联系,是有效进行角变换的前提。常用的角变换关系有:α=(α+β)-β,α=(α-β)+β,2α+β=2(α+β)

二、辅助角变换的技巧


三、整体换元的技巧
在三角恒等变换中,也可把一个代数式整体视为一个“元”来参与计算和推理,这个“元”可以明确地设出来,如令t=sinx-cosx。
例3 求函数y=sinx+sin2x-cosx(x∈R)的值域。

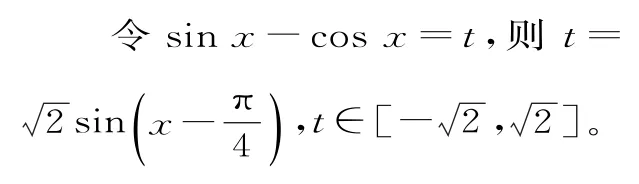
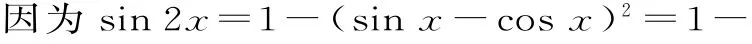

整体视为一个“元”的本质为消元策略,但要注意新元的取值范围。
猜你喜欢
中学生数理化·七年级数学人教版(2022年5期)2022-06-05
中学生数理化·七年级数学人教版(2021年12期)2021-12-31
中学数学杂志(高中版)(2019年1期)2019-04-02
中学教学参考·理科版(2017年8期)2018-02-24
中国总会计师(2017年10期)2017-12-13
中学生数理化·高三版(2017年2期)2017-04-21
福建中学数学(2017年1期)2017-04-21
中学生数理化·七年级数学人教版(2016年4期)2016-11-19
中学生数理化·七年级数学人教版(2016年4期)2016-11-19
中学生数理化·七年级数学人教版(2015年4期)2015-05-30

