基于分层布线算法集成电路通道布线最优策略

顾家畅 黄 鑫 邓 谯

(湖南农业大学信息与智能科学技术学院,湖南 长沙410128)

1 概述

集成电路在生产生活的方方面面都有着十分重要的作用，随着技术的发展，其内部的元器件数量已达到了十亿级别，需借助电子设计自动化（EDA）工具才能完成电路的设计与实现。“物理设计”是其中一个重要阶段，先将器件摆放在合适的位置，然后用金属线连接器件实现连接关系，后者称为“布线”，布线可用区域由nxm个方格组成，金属线允许沿着直线或直角（方格）放置。由于金属线引入的寄生电阻会影响电路性能，所以需要最小化布线长度。本文重点考虑“布线”问题中的一个特例：“通道布线”，“通道”是指一个横向的布线区域，区域的顶部和底部分布着需要连接的方格，需用金属线将相应的引脚连通起来。

2 问题分析

本文通过对一层通道布线图的分析，可知依据原方格图会存在求解复杂的缺点，因此将用无网格布线算法[2]对通道布线图变线宽、变线距问题进行优化，以此提高了布线的速度，也得到较好的效果。基于附件测例数据及一层通道布线原则，将对各上、下引脚坐标进行分析，上引脚坐标、下引脚坐标中的i的变化将暴露其造成短路的问题，其中如果i>i+1则此测例无解。从而会得到一层金属通道布线问题的答案，并且在以上分析的基础上，尽力消除寄生电阻的影响保持电路性能较好的前提下，可利用曼哈顿公式求得引脚布线的曼哈顿距离最小，即为最小化布线长度。

在上述分析的基础上可知：在何种情况下，一层金属通道布线问题无解，此时将考虑多个金属层情况，以3层金属通道布线为例，在测例3数据的基础上，根据上下引脚坐标中i的变化规律进行动态规划，在上引脚坐标i依次递增的前提下确保下引脚坐标i尽量递增，再将上下引脚坐标i变化较大的进行层层筛选，通过计算机软件的处理可得到分成3部分的引脚对数，此时可将数据最多的一部分作为基础层，将依据i值变化的大小得到第二、三层的引脚对数。接下来,可以通过分层布线算法[3]，依据靠左或靠右原则连接每对引脚为其合理布线，在合法域内为必要的部分增加通孔连通，再利用曼哈顿公式求解模型，从而可得到测例三数据中符合要求的3层金属通道布线的最小布线长度。

3 模型建立

根据无网格布线算法，对测例1数据进行了处理，得到的测例1无网格布线图如下图1所示。

图1 测例1一层通道布线无网格布线图

其中每个点代表每原方格的中心，相邻两点间的距离为单位1，由上图可知测例1中每对引脚都可以成功布线，且不会短路。

同样的方法，我们对测例2、3的数据进行一层通道布线图拟合，如附录图所示，可发现这两种情况均会出现同一个点有不同路线经过的情况，不满足题目条件，也即该情况一层通道布线问题无解。

对于测例1数据有解情况，由平移定理可知：在每个引脚对的合法区域中，当行驶不重复方向时，最短路径为合法区域的垂线边界与水平线边界，又因宽度相同，因此我们可利用曼哈顿距离公式进行最小化布线长度求解，假设在最新无网格布线图中每个引脚对的上引脚坐标为（Ai，Aj），下引脚坐标为（Bi，Bj），则可用曼哈顿距离公式求得引脚布线长度为：

在此基础上，问题一的最小布线长度为d1，设总的引脚数为K，k代表第k个引脚，则测例1的一层通道布线最短长度为：

在对测例数据的分析后，可得在何种情况下，一层金属通道布线问题无解。同时将测例1的引脚坐标数据代入曼哈顿距离公式，通过计算我们可以求得，布线长度为16，即16个网格。

通过网格点化并建立直角坐标系得到上下引脚的坐标，从第一层开始，从左到右地将引脚进行连接，并保证连线尽可能地靠左连接，另一边尽可能的靠右连接，得到两条极端路径，分别称为这对引脚的左合法边界和右合法边界，两条边界共同围成的闭合区域我们称为合法域，具体如下图2所示。当第n对引脚对的左合法边界同时与第i对的右合法边界和左合法边界相交时，这时我们认为第n对和第i对引脚对不能在同一层完成金属布线。两个引脚对的合法域的相交区间，称为共有域。同时在引脚对合法域内，每一条从上引脚全程向着下引脚走的任何一条通路都是该引脚对连接的最短路径。对则需要在可用布线空间最下方留出α行空白网格。

图2 合法区域概念图

（6）第一层通道布线完成后，将前面数据筛选过后的其它层的引脚对路径按照同样的方式进行排列。

（7）在除去第一层单都其它层引脚对集合进行通道布线时，需要选择通孔的位置，通孔的位置优先在每对引脚对的合法域内进行选择，若无合适位置则优先考虑在距离合法域最近的无干扰布线区域进行选择。

（8）通道布线长度的距离计算公式：

4 模型求解

本文采用多个金属层来进行通道布线，我们以测例3的引脚数据为例来进行模型的建立与求解。通过计算机软件将测例3的36对引脚分成三组，以上引脚次序依次递增的前提下尽量保证下引脚坐标依次增大，再将不符规律的分为二、三组，且把上下引脚坐标跨度最大的作为第三组，分组后的数据如下：

第 一 组 （1,3），（2,4），（3,5），（5,6），（9,7），（10，9），（11,10），（12,14），（13,15），（14,16），（16,17），（20，18），（21,20），（22,21），（23,25），（24,26），（25,27），（27,28），（31,29），（32,31），（33,32），（34,36）,（35,37），（36,38），（38,39），（42,40），（43,42），（44,43）

第二组（6,8），（17,19），（28,30），（39,41）

第三组（4，11），（15,22）,（26,33），（37,44）

其中，第一层布线为实线，第二层为虚线，第三层为粗线，最上层点和最下层的点为上下引脚所在位置，黑色的点为布线空间

图3 三层通道布线图

（1）令初始的引脚对集合为：

依据Aki从大到小进行排列。

并将其它引脚对储存到第一层引脚对集合中：

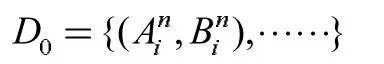
（3）重复上述数据筛选步骤，将D0筛选的数据剔出放入D1中，将D1的数据筛选后继续提出放入新的引脚对集合中，直到所有集合中没有无干扰布线。

基于该测例数据，按照上述的模型二，我们可以找到测例3的最优通道布线，并通过优化的曼哈顿距离计算公式可求得最小化布线长度为160。

5 后续研究

新通孔制造工艺要求任意两个通孔的间距必须大于等于2个格点，通过对分层布线和合法区域的判断，能够找出通孔可选择区域，在可选择区域内增添通孔设置区域的条件为大于等于2个格点。因此，增加在合法区域内所有未占用点为圆心，以2为半径画圆，而在此圆外或边界上的点，可以成为此引脚对可选择设定通孔的位置，最后利用曼哈顿公式求解模型，将得到符合要求的最小布线长度。