改进的和声搜索算法求解多目标优化问题∗

谷培义 高 尚

（江苏科技大学计算机学院 镇江 212000）

1 引言

多目标优化是运筹学中的重要部分，同时也是科学研究和社会生活中普遍存在的一类优化问题。在多目标优化问题中，相同的变量因素，相同的变化，往往造成不同的目标产生相反的变化，使得最优选择的寻找变得十分困难。因此，多目标优化问题一直是各个学科研究者的研究对象。随着进化算法的出现与不断发展，前人提出了许多优化的多目标进化算法，如：非劣排序遗传算法（NS⁃GA）［1］及其改进算法NSGA-II［2］，强度Pareto进化算法（SPEA）［3］，多目标遗传算法（MOGA）等［4］。在多目标优化问题的求解上这些算法在不同的方面有不同的优势，对于多目标优化问题的求解具有较好的表现，但也存在着一定的改进空间［5］。

和声搜索算法（Harmony Search Algorithm）在求解单目标连续问题上取得了较好的效果［6］，在某些实际问题上的应用也取得了较好的表现［7］，但在解决多目标问题上，和声搜索算法出现了收敛速度慢，容易陷入局部最优解等问题［8］。

本文在和声搜索算法的基础上，通过引入自适应操作［9］，提出了一种改进的多目标和声搜索优化算法，使和声搜索算法的关键参数动态变化，根据迭代次数产生合适的参数值，从而增强了算法的全局搜索能力，增加解的多样性；同时对解集根据Pa⁃reto最优解［10］进行非支配排序，每次选取解集非支配排序中最优部分的解进行和声微调，以此来提高算法效率，增加算法在后期的收敛精度。最后根据仿真实验和评价标准对改进后的算法进行评测。

2 基本和声搜索算法

和声搜索（Harmony Search，HS）算法［11］是一种启发式算法，是模仿音乐家即兴创作而产生的，由Geem.Z.W等在2001年提出。类似地还有其他典型的智能优化算法，如蚁群算法对蚂蚁行为特性的模拟仿真，遗传算法对生物进化的模仿，模拟退火算法对物理退火机制的模仿等。

音乐演奏是一个寻找优质的和声的过程，调整演奏出在美学评价中的最佳状态［12］。对比之下，优化算法也是根据目标函数求解出最符合目标函数预期值即最优解的过程。对应的目标函数值则是由相关变量值的解组成的集合求解得到。如音乐演奏中的优质和声，是参与演奏的各个乐器的声音集合。

在HS算法中，主要有四个变量参数：和声库大小（HMS），和声记忆库保留概率（HMCR），扰动概率（PAR）以及音调微调幅度（BW）［13］。

基础和声搜索算法流程（见图1）。

图1 HS算法的流程图

3 多目标优化问题及评价标准

3.1 多目标优化问题基本概念

多目标优化问题是在各个变量因素变化范围内综合考虑不同的目标，根据需求得出的最优解集。一个具有m个目标变量、n个决策变量的多目标优化问题，可表示为

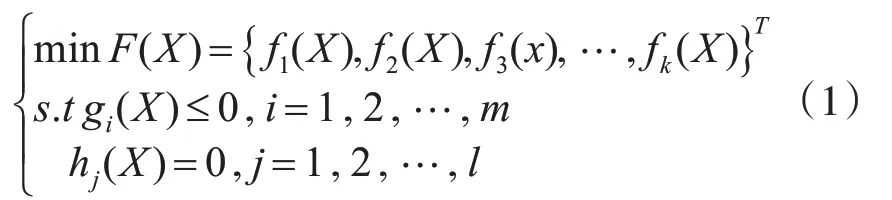
式中：X为决策变量，X=(x1，x2，…，xn)T，n为向量X的维数；fk(X)是k个目标k=1，2，…，p，p为目标函数的个数；gi(x)是第i个不等式束；m为不等式约束数目hj(x)是j个等式约束；l为等式约束数目。

文献［14］提出了关于多目标优化的一些基本概念。

定义1（支配）：向量U=(u1，u2，…，uk)被向量V=(v1，v2，…，vk)支配当且仅当：

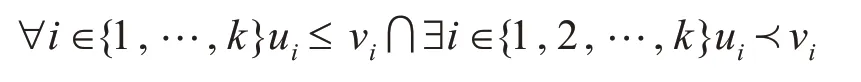
定义2（Pareto最优解集）：对于任意的X∈Ω，不存在X满足f(X)≺f(X*)，则X*是Pareto最优解。

定义3（Pareto最优解集）对一个多目标优化问题F(X)，它的最优解集为

定义4（Pareto前沿）：对于一个给定的多目标优化问题F(X)和它的Pareto最优解集P*则它的Pareto前沿(PF*)定义为

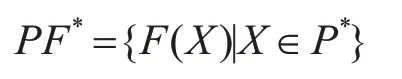
多目标优化问题的目标函数之间是相互影响的，通常情况下，一个变量参数的变化，可能会导致其中一个目标函数的结果变差，同时反而会让另一个目标函数的结果变好。目标函数之间彼此冲突，因此，多目标优化算法目的是最优化求解出一系列非支配解，这些Pareto最优解可以尽可能地协调各个目标函数结果的好与差。

3.2 多目标优化问题评价标准

多目标优化算法性能的主要评价指标为收敛性和多样性。Deb等在文献［15］中提出的收敛性指标ϒ和多样性指标Δ来评价

1）收敛性指标：

其中，n为所求解出的非支配解的个数，di为第i个非支配解与理论Pareto前沿的最小距离。收敛性指标数值越小，说明算法所求解越接近Pareto最优前沿。

2）多样性指标

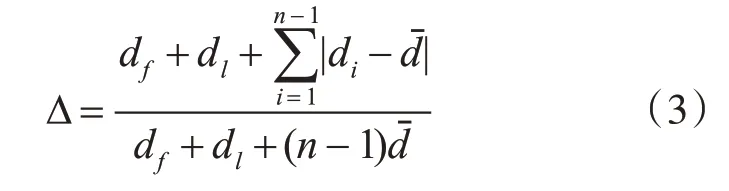
其中，n为求解出的支配解个数，di为相邻两个个体之间的欧氏距离；dˉ为di的均值；df、dl是求解出的非支配解中的两个边界解与极端解的欧氏距离。Δ越小，代表算法的多样性越好［16］。

4 改进的和声搜索算法（GHS）

4.1 参数自适应

传统的和声搜索算法参数微调概率（PAR）和音调微调幅度（BW）算法运行过程中是固定值，因而算法易陷入局部最优。和声搜索算法中也有很多改进的方法被应用其中［17］，本文算法中PAR根据式（4）动态变化，BW根据式（5）动态变化。

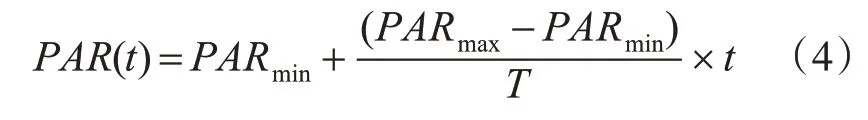
式中PAR(t)是随着迭代次数t变化的，t是当前迭代次数，PARmax是最微调概率取值上限，PARmin是微调概率取值下限，T是总的迭代次数。

式中BW(t)是随着迭代次数t变化的，BWmax是调整幅度取值上限［18］，BWmin是调整幅度取值下限。

4.2 Pareto非支配排序

首先解集中的每个解都与解集中其他解进行支配关系比较，是否支配其他解，记录每个解的被支配个数k，根据k值对解集中的解进行排序。

然后，k相同的解按照相邻的解距离大小（D）按照从大到小排序。D按照式（6）计算。目标函数的边界值的D取无穷大。

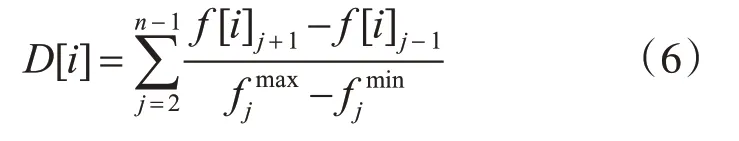
式中D[i]表示第i个解的距离，n表示目标函数的数量，f[i]j+1表示第i个解的第j+1个目标函数的值，f[i]j-1表示第i个解的第j-1个目标函数的值。表示第j个目标函数的最小值和最大值［19］。

4.3 GHS算法步骤

Step1：算法参数：N（解集大小），T（最大迭代次数）。

Step2：在定义域范围内先随机产生一个解集P0。

Step3；在P0基础上利用自适应和声搜索算法产生一个新的解集Q0，P0和Q0的解集大小都为N。

Step4：将Pt和Qt并入到Rt中（初始时t=0），Rt大小为2 N，对Rt进行非支配排序，得到一个按照k值大小从小到大排序的解集，得到不同等级的非支配解集。

Step5：Rt取前N个解存入Pt，形成新的解集。

Step6：若t≥T则终止搜索；否则转入Step3。

5 实验测评

本文的实验选取文献［15］中的四个目标函数ZDT1、ZDT2、ZDT3和ZDT6来分别进行测验，并在算法收敛性和多样性方面与NSGA-II、SPEA2［20］这两个多目标优化算法进行比较。参数设置：解集数量N=200，最大迭代次数T=500，PARmax=0.95，PARmin=0.5，BWmax=0.1，BWmin=0.001。实验分别对三种算法均独立运行20次，三种算法的结果进行相互比较。通过表1和表2对比，改进后的HS在解决多个目标优化问题时，Pareto最优解集的ϒ和Δ两个指标值，总体要优于NSGA-II和SPEA2两种多目标优化算法。因此改进后的和声搜索算法能够更有效地求解多目标优化问题。

表1 基于ϒ的统计结果比较

表2 基于Δ的统计结果比较

GHS所得Pareto前沿图与真实的Pareto前沿图对比，如图2～5。

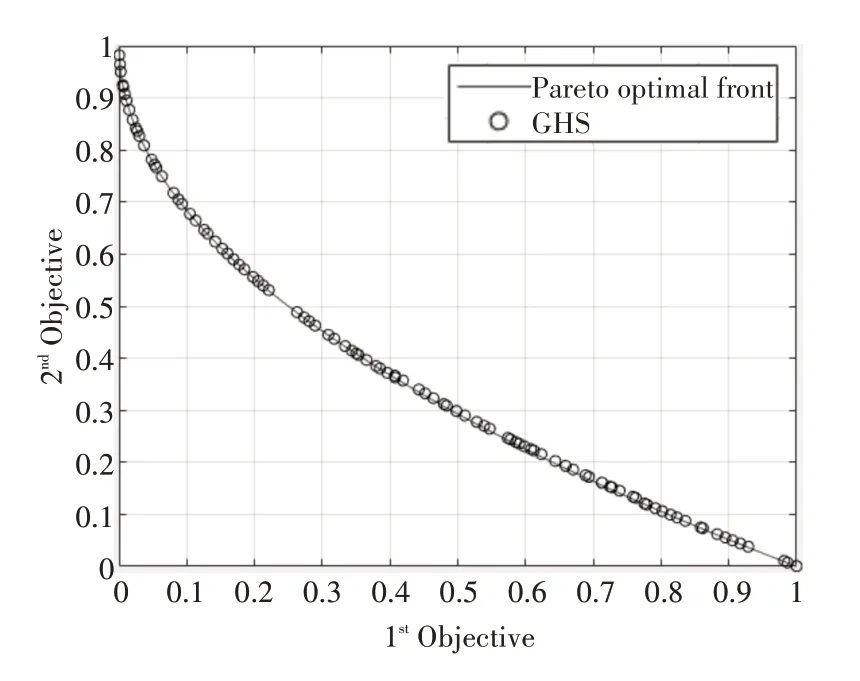
图2 ZDT1测试函数算法对比图

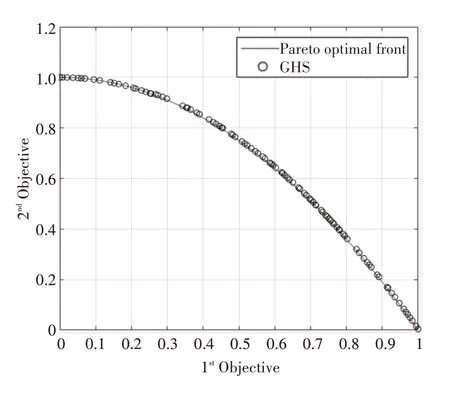
图3 ZDT2测试函数算法对比图

图4 ZDT3测试函数算法对比图

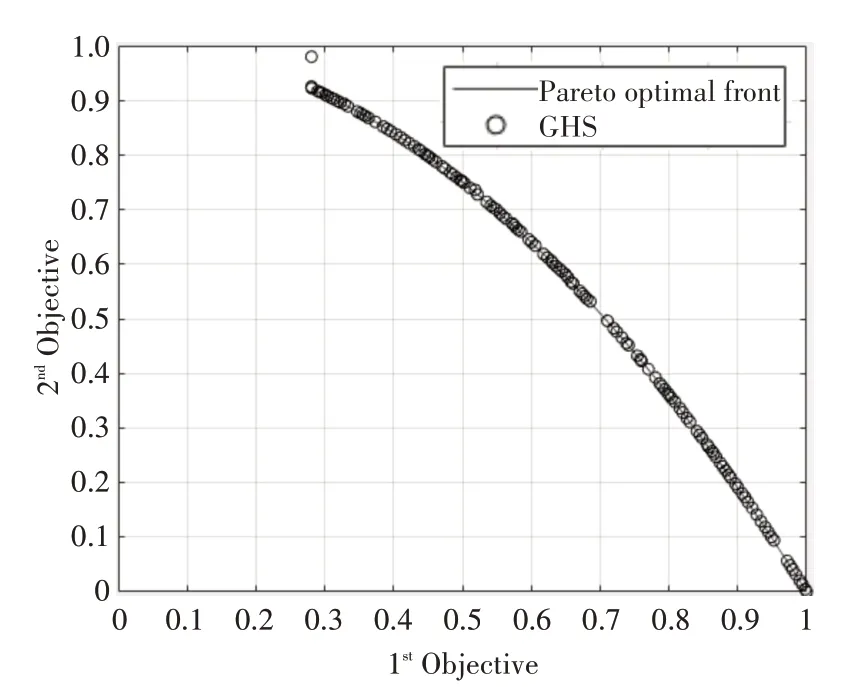
图5 ZDT6测试函数算法对比图

6 结语

本文提出了一种改进的多目标和声搜索算法，引入参数自适应操作，使和声搜索算法的关键参数动态变化，根据迭代次数产生合适的参数值，从而增强了算法的全局搜索能力，增加解的多样性；同时对解集根据Pareto最优解进行非支配排序，每次选取解集非支配排序中最优部分的解进行和声微调，提升了算法效率和算法在后期的收敛精度。最后通过实验测评，测评数据表明该算法具有较好的收敛性和多样性。