中空夹层钢管混凝土长支撑构件受压性能研究

黄炎生 罗济杭 韩姝妤

摘 要：针对地铁基坑支护的支撑选取问题，提出了一种中空夹层钢管混凝土长支撑构件，采用有限元软件ABAQUS对构件进行模拟，研究其在压力作用下的承载能力及破坏特性，并分析了长径比、空心率对其轴压力学性能的影响以及长细比、荷载偏心距、空心率对其偏压性能的影响。结果表明：长径比对中空夹层钢管混凝土长支撑构件的轴心受压性能有显著影响，空心率对轴心受压性能影响不大;长细比、荷载偏心距对中空夹层钢管混凝土长支撑构件的偏心受压性能有显著影响，空心率对偏心受压性能影响不大;现有短构件受压极限承载力计算公式同样适用于本文提出的长构件。

关键词：中空夹层钢管混凝土;地铁基坑支撑;有限元;轴心受压;偏心受压

中图分类号：TU398.9  文献标志码：A

在大跨度地铁基坑支护中，若使用常规的钢支撑构件，存在构件计算长度过长，不满足规范要求的问题。中空夹层钢管混凝土具有承载能力高、延性好、自重轻等特点[1]，且在现行规范中，对钢管混凝土支撑构件无长度上的要求，故在大跨度地铁基坑支护支撑的选取过程中，可以考虑采用中空夹层钢管混凝土的长支撑构件。

目前对于中空夹层钢管混凝土的研究已有诸多报道，UENAKA等[2]研究了外管径厚比、空心率等参数对短柱破坏形态的影响;陶忠等[3]总结了适用于实际工程的轴压及偏压承载力计算公式;黄宏[4]研究了宽厚比对于外方内圆截面构件延性及外钢管屈服的影响;HASSANEIN[5-7]等给出了适用于实际工程的径厚比范围;ZHANG等[8]提出了局部受压极限强度的简化模型;王志滨[9]总结出适用于薄壁钢管短柱构件的轴压承载力简化计算公式;国外众多学者[10-12]也对各种形式的中空夹层钢管混凝土短柱轴压及偏心受压性能进行了不同的研究。然而，目前关于中空夹层钢管混凝土长构件的受力性能的相关研究比较少，且无针对带节点的中空夹层钢管混凝土长支撑构件的性能研究。为探究该类型构件的承载能力及破坏特性，本文对其进行了有限元模拟，研究了空心率、长细比、偏心率等因素对构件受力性能的影响。

1 分析模型设计

1.1 试件设计

结合工程实际，选取典型构件CCL-3000作为标准构件，构件长度L=3 000 mm，内外钢管壁厚t=5 mm，钢管外径D=300 mm，内径D0=180 mm。标准构件长径比L/D=10，空心率为0.62。钢材采用Q345，屈服强度470 MPa，弹性模量2.02×105 MPa，混凝土采用C30。

设置了5组共30根构件，分别研究长径比、空心率对其轴压力学性能的影响与长细比、荷载偏心距、空心率对其偏压性能的影响，如表1—表4所示。表中仅对与CCL-3000构件不同的参数进行说明，未注明的参数均与CCL-3000相同。1.2 计算前的准备

钢管的本构模型选取理想弹塑性模型（简单的二折线模型），混凝土的本构模型选取刘威[13]提出的适用于圆钢管混凝土有限元模拟的等效应力-应变关系模型;对于单轴受拉本构模型，采取规范[14]定义的应力-应变关系。

采用壳单元（S4R单元）模拟内外钢管，采用八节点线性减缩积分实体单元（C3D8R单元）模拟核心区域混凝土。钢管混凝土构件中内外钢管与核心区混凝土的接触方式分为法线方向的接触与切线方向的接触。对于法向方向的接触，采取硬接触（“Hard” Contact）模式;对于切线方向的接触，采用库伦摩擦模型，摩擦系数取μ=0.25。端板与构件之间采用绑定约束（Tie）模式。在构件模型中，需引入初始缺陷以使模型接近于真实加载情况，本文引入一階模态作为构件的初始几何缺陷模态，取构件长度的1/1 000。

因为缺乏试验数据的验证，为验证本文有限元模型计算结果的可靠性，先选取文献[15]中的圆中空夹层钢管混凝土短柱模型SFTZ165（0.38），SFTZ165（0.55），SFTZ165（0.72）进行模拟。得到与试验结果基本一致的结果，极限承载力相对误差均在10%以内，平均误差为-7.32%;且破坏形态相同，在构件端部及中部出现了鼓曲，证明有限元模拟结果与试验结果具有较好的吻合度.

2 计算结果分析

2.1 长径比对轴压性能的影响

以1.1节中的CCL-3000构件为标准构件，并以构件的长径比作为参数变量进行分析。由构件破坏形态（图1所示）可知，不同长径比构件的破坏形态大体相同。当长径比小于15时，构件外钢管跨中挠曲较大，且鼓曲部位的应力为最大值;长径比大于20时，构件外钢管没有明显挠曲现象。长径比较小的构件破坏时核心混凝土的应变接近极限应变，接近强度破坏，而长径比较大的构件核心混凝土的塑性应变小于混凝土的极限压应变值，混凝土强度未得到充分发挥，构件由于失稳而破坏。

图2为构件承载力随长径比变化的规律，长径比越大，构件的极限承载力越小。长径比越大的构件，对应的破坏位移越大，但当长径比大于25时，破坏位移基本不变。说明对于长径比不大的构件，随着长径比的增加，构件延性越好;但对于长径比大于25的细长构件，构件的延性基本没有差别。

2.2 空心率对轴压性能的影响

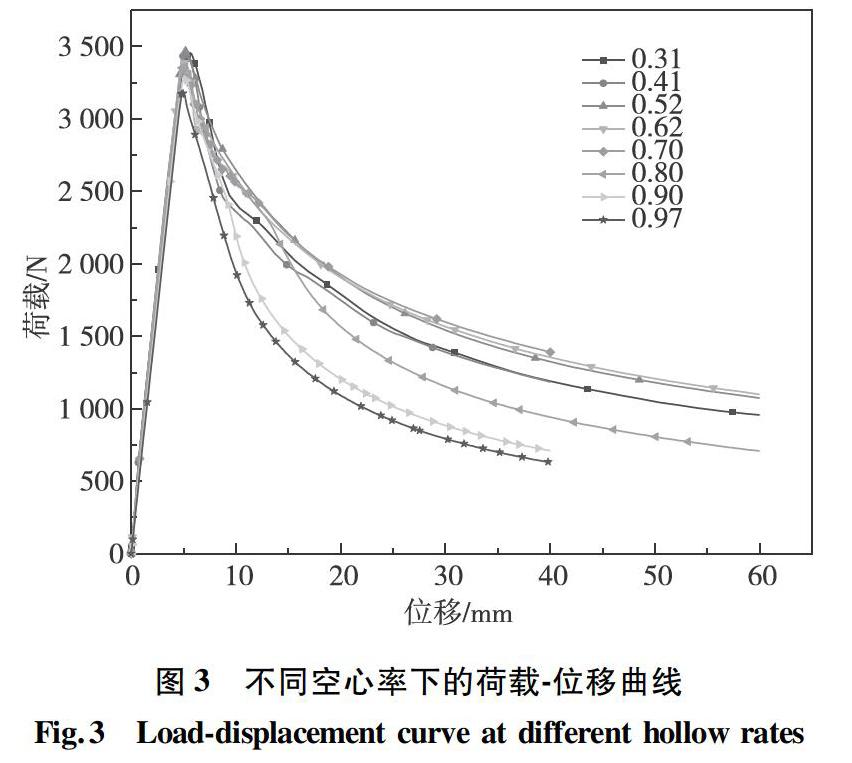
如图3所示，随着构件空心率增加，极限承载力的下降并不明显。对于不同空心率的构件，极限承载力对应的位移均为5.0 mm左右，各试件均表现出一定的延性，且空心率为0.5～0.7之间的构件延性较好，与规范[16]中空心钢管混凝土空心率不宜大于0.75的建议一致。

2.3 荷载偏心距对偏压性能的影响

由图4可以看出，随着荷载偏心距的增加，极限承载力与轴压的差值逐渐增大，但变化幅度逐渐减少，荷载偏心距从0 mm增加80 mm时，极限承载力从3 397.31 kN下降至1 760.98 kN。弹性阶段抗压刚度（即初始弹性阶段荷载与位移的比值）的变化则呈非线性趋势，当荷载偏心距小于30 mm时，每增加10 mm，抗压刚度平均下降5.78%，大于30 mm时平均下降速度为36.48%。荷载偏心距越大，极限承载力对应的位移也逐渐增大，之后的下降曲线也逐渐平缓。

2.4 長细比对偏压性能的影响

由图5可以看出，随着构件长细比的增加，极限承载力随之降低，当长细比小于52时，构件的极限承载力变化幅度仅为1%左右;当长细比大于52时，由于构件趋向于失稳破坏，极限承载力下降幅度大幅增加，达到10%左右，当长细比大于87时，下降幅度增加至20%。随着长细比的增加，构件在弹性阶段的抗压刚度也逐渐减少，当长细比为35～122之内时，降幅平均为20.78%，且变化呈非线性趋势，变化曲线内凸。

2.5 空心率对偏压性能的影响

由图6的荷载-位移曲线可知，不同空心率下的偏压试件荷载-位移曲线走势基本一致，弹性阶段的抗压刚度、极限承载力与其对应的位移都基本相等，且后期都出现了不同幅度的曲线强化现象，均表现出一定的延性。此外，随着空心率的增大，内管直径不断增大，中和轴逐渐向内管靠近，内管塑性得到充分发展。

3 构件承载力计算

结合文献[17]提出的圆中空夹层钢管混凝土轴压承载力计算公式，对上文中的有限元模拟结果进行验证。由对比数据可知，有限元模拟值与计算值的比值在0.83～0.99之间。其中，不同长径比结果的比值平均值为0.90，随着长径比的增大，模拟值与计算值的差距增大;不同空心率结果的比值差距较小，平均值为0.95。理论公式计算值大于有限元模拟结果，吻合程度较好，证明了上文模拟结果的正确性，且文献[17]中的短柱轴压公式大致适用于长构件，计算结果见表5。

结合文献[17]提出的适用于中空夹层钢管混凝土构件的N/Nu-M/Mu曲线相关方程，用偏压有限元模拟结果进行验证。由图7可知，由于空心率大的构件钢材占比大，其N/Nu-M/Mu曲线更接近钢材的相关曲线形状，且随着空心率增大，N/Nu-M/Mu中M/Mu小于1部分的曲线长度增加，大于1部分的抛物线长度减短，由分段函数曲线向线性函数曲线转化。对于长细比对比组，大部分计算值大于有限元模拟值，且当长细比小于λp即87时，误差均在10%以内。当长细比大于87时，长细比对构件极限承载力的影响增大，导致模拟值与计算值存在较大误差。计算结果见图8和表6。从结果来看，文献[17]所提的计算公式与有限元模拟结果在长细比较小的情况下比较接近，可用于计算构件的承载力。

4 结论

（1）中空夹层钢管混凝土长构件在轴压下的荷载-位移曲线可分为弹性、弹塑性、塑性三阶段。其极限承载力随长径比增大而减小，空心率增加，极限承载力下降并不明显，但空心率为0.5～0.7的构件延性较好。

（2）中空夹层钢管混凝土长构件在偏压下的荷载-位移曲线也可分为弹性、弹塑性、塑性三阶段。当长细比小于52时，构件的极限承载力变化不大，大于52时开始以10%左右的速度下降，大于87时，下降幅度增加至20%，抗压刚度变化也呈非线性趋势。

（3）长径比、空心率变化时，轴压构件极限承载力有限元模拟结果与文献[10]的公式计算结果较吻合，说明文献[10]公式可适用于本文设计的长构件。

（4）大空心率构件的N/Nu-M/Mu曲线形状更接近钢材相关曲线形状，且趋于线性函数关系;且长细比λ<λp时，有限元模拟极限承载力与公式计算结果相差均在10%以内。

参考文献：

[1] 韩林海.钢管混凝土结构[M].北京： 科学出版社， 2000.

[2] UENAKA K， KITOH H， SONODA K. Concrete filled double skin circular stub columns under compression[J]. Thin Walled Structures，2010，48（1）：19-24.

[3] 陶忠， 韩林海， 黄宏. 圆中空夹层钢管混凝土柱力学性能研究[J]. 土木工程学报， 2004， 37（10）： 41-51.

[4] 黄宏， 张安哥. 方中空夹层钢管混凝土轴压构件的试验研究[J]. 铁道建筑， 2007（5）： 10-12.

[5] HU H T， SU F C. Nonlinear analysis of short concrete-filled double skin tube columns subjected to axial compressive forces[J]. Marine Structures， 2011， 24（4）： 319-337.

[6] HASSANEIN M F， KHAROOB O F， LIANG Q Q. Circular concrete-filled double skin tubular short Columns with external stainless steel tubes under axial compression[J]. Thin-Walled Structures，2013，73：252-263.

[7] HASSANEIN M F， KHAROOB O F， GARDNER L. Behaviour and design of square concrete-filled double skin tubular columns with inner circular tubes[J]. Engineering Structures， 2015， 100：410- 424.

[8] ZHANG Y B， HAN L H， LI W. Analytical behaviour of tapered CFDST stub columns under axially partial compression[J]. Journal of Constructional Steel Research， 2017， 139： 302-314.

[9] 王志濱，郭俊涛，高扬虹，等.中空夹层薄壁钢管混凝土短柱轴压性能研究[J].建筑钢结构进展，2018，20（2）：53-59.

[10]ELCHALAKANI M， PATEL V I， KARRECH A， et al. Finite element simulation of circular short CFDST columns under axial compression[J]. Structures， 2019， 20：607-619.

[11]VERNARDOS S， GANTES C. Experimental behavior of concrete-filled double-skin steel tubular （CFDST） stub members under axial compression： a comparative review[J]. Structures， 2019， 22：383- 404.

[12]EKMEKYAPAR T， HASAN H G. The influence of the inner steel tube on the compression behaviour of the concrete filled double skin steel tube （CFDST） columns[J]. Marine Structures， 2019， 66： 197-212.

[13]刘威. 钢管混凝土局部受压时的工作机理研究[D]. 福州： 福州大学， 2005.

[14]中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB 50010—2010[S].北京： 中国建筑工业出版社， 2010.

[15]杨静. 圆中空夹层钢管自密实混凝土短柱的轴压力学性能试验研究[D]. 乌鲁木齐： 新疆大学， 2016.

[16]中华人民共和国住房和城乡建设部.钢管混凝土结构技术规范： GB50936—2014[S].北京：中国建筑工业出版社， 2014.

[17]黄宏. 中空夹层钢管混凝土压弯构件的力学性能研究[D]. 福州： 福州大学， 2006.

（责任编辑：于慧梅）

Abstract： A type of concrete-filled double-skin steel tube（CFDST） long support member is put forward to solve the problem of selecting subway foundation pit support. The finite element software ABAQUS was used to simulate the member. The failure mode and bearing capacity under compression were studied. The influence of length-to-diameter ratio and hollow rate on the axial compression behavior and the influence of slenderness ratio， load eccentricity and hollow rate on the eccentric compression behavior were analyzed. The research results show that the length-to-diameter ratio have significant effects on the axial compression behavior of the CFDST long support member， and the hollow rate has little effect; the slenderness ratio and load eccentricity have significant effect on the eccentric compression behavior of the CFDST long support member， and the hollow rate has little effect. The existing calculation methods of CFDST short members are also applicable to long members put forward in this paper.

Key words： concrete-filled double-skin steel tubes; subway foundation pit support; finite element analysis; axial compression; eccentric compression