考虑负载均衡与传输速率的异构网络接入控制

刘丽娟，刘定一，陈松楠,3

(1.信阳农林学院 信息工程学院，河南 信阳 464000；2.河南警察学院 网络安全系，河南 郑州 450046； 3.北京林业大学 工学院，北京100083)

0 引 言

近些年无线终端用户的数量出现了爆发式的增长，且对视频业务的需求量也越来越大，这就需要更多的频谱资源来满足不同的业务接入。由于固定单一的网络频谱资源有限，当大量用户有业务请求时，不仅会出现接入成功率低的情况，还会影响在线用户的使用体验[1]。当无线终端处在多种不同类型的异构网络覆盖中时，运营商会根据业务类型和网络资源的剩余情况，将不同的业务接入到最适合的网络中，保证资源的利用率及用户的使用体验。从运营商的角度考虑，会优先关心网络的负载均衡问题，因为非均衡的网络容易出现接入成功率低和阻塞的问题；而从用户的角度考虑，则希望得到最大的传输速率[2-4]。

在生活中往往会遇到此类问题，在满足一定的约束条件下，希望两个或两个以上相互冲突的目标达到最优，统称为多目标优化问题(MOP)[5-7]。MOEA/D算法可以更高效地求解高维多目标优化问题，得到的解集精确，且计算复杂程度低[8,9]。但在MOP中仍然存在收敛性和多样性相互制约的问题，学者们也相继提出了很多的改进方法。文献[10]采用精英策略和差分进化修正的方法进行全局搜索，提高了算法的收敛精度和全局搜索能力；文献[11]设计了自适应的变异算子和邻域值，有效改善了算法的全局搜索能力和收敛性；文献[12]引入了多策略变异，并通过采取非支配排序，选取更优的解来实现差分进化，改善了算法的收敛速度和多样性。然而，上述这些方法在平衡算法的多样性和收敛性方面仍有不足，为此本文在优化了聚合函数的基础上，从变异概率和邻域两个方面提出了自适应的改进策略，并将其应用在异构无线网络的业务接入控制中，来解决网络负载平衡和系统传输速率的问题，最后通过实验验证了方法的有效性。

1 建立异构网络模型

假设在某区域存在N个异构无线网络，在其重叠覆盖的空间有M个多模终端，采用多用户正交频分复用(OFDM)的方式进行数据传输，其中最小的资源计量单位是1个时隙和1个子信道组成的二维资源单元(TRU)[13]。若网络k的子载波数量为Nk，每个子信道中有Fk个子载波，那么网络k的最大资源TRU可表示如下

(1)

式中：SPk表示OFDM的符号周期；Sk表示每个时隙中符号的数量；TSk表示数据帧的长度。

假设用xjk来描述终端业务与网络的连接情况，当终端业务j接入网络k时，xjk=1，反之，则xjk=0。那么M个终端业务与N个网络就形成的映射关系，可表示成1个M×N的矩阵，矩阵的元素为xjk。若网络k连接到终端业务j要占用的资源数是tjk，那么所有的业务消耗网络k的资源总数为

(2)

联合式(1)、式(2)可计算网络k的负载率描述如下

(3)

假设终端业务j占用网络k的信道带宽为bjk，利用香农定理可计算出网络k的数据传输速率rk如下

(4)

式中：ωjk为效益因子；Sjk为信号功率；Njk为噪声功率。

本文将最小网络间负载率方差V和所有网络系统传输速率的倒数R作为优化的目标函数进行组合，转化成多目标优化模型。

根据网络负载率式(3)，最小网络间负载率方差函数V可描述如下形式

(5)

根据网络传输速率式(4)，对所有网络中业务的传输速率进行累加，再对其求倒数，将其最小值(也就是系统最大速率)作为优化函数R可描述为

(6)

对于单个网络来说，其能提供的资源是有限的，所以接入该网络所有的资源数不能大于其能提供的总数，产生约束条件描述如下

(7)

另外，对于终端业务接入网络的数量有限制，即每个业务最多只能与1个网络进行连接，产生约束条件描述如下

(8)

2 多目标优化问题及MOEA/D算法

由于MOP之间的解往往相互制约和冲突，当一个目标的解较好时，另外一个解就会变差，所以MOP的解并不唯一，而是一组最优的解集，这就需要在参数设置时，要根据实际的需要进行折中选择[14,15]。终端业务的接入方式(即终端与网络的映射关系)决定了不同网络间的负载平衡和系统的传输速率，属于多目标优化问题。故本文以接入方式作为变量，将最小负载率方差函数和系统最大传输速率的倒数作为目标函数，并结合2个约束条件进行组合，转化成多目标优化模型，利用改进的MOEA/D算法进行求解，得到最优的接入方案。

2.1 多目标优化问题描述

针对m个目标的优化问题，设其具有n个决策变量，对应的决策向量为x=(x1,x2,…,xn)∈Rn，通过数学表达进行描述如下

(9)

式中：Ω表示可行域空间；Ω→Rn有m个目标函数，分别为f1(x)，f2(x)，…，fm(x)。

为了能够更加清楚表述多目标优化问题，对以下问题进行了定义：

定义1 Pateto支配：若x,y∈Ω是可行解，对于任意的i=1,2，…，m，当且仅满足式(9)时，那么xPateto支配y，计作xy

(10)

定义2 Pateto最优解集：MOP的最优解是由多个Pateto最优解组成，即所有的最优解称为Pateto最优解集(Pateto set，PS)，或者称为非支配解，表示为

(11)

定义3 Pateto最优前沿：Pateto最优解集在目标空间的投影对应的就是Pateto最优前沿(Pateto front，PF)，表示为

PF={F(x)|x∈PS}

(12)

2.2 MOEA/D算法框架分解

MOEA/D算法的核心思想是将多目标问题分解成多个单目标问题进行求解，经典的分解方法有：加权和、切比雪夫和PBI这3种方法[16]。其中，最常用的是切比雪夫法，通过在单目标上增加权重来进行变换，这个分解的过程表示如下

(13)

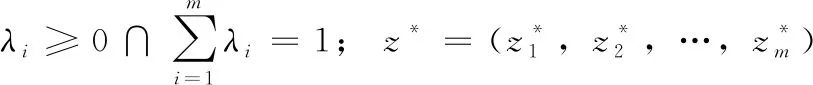
由于MOEA/D算法本质上属于迭代的过程，在每次的迭代中都会保持种群的个体数量n，分别为x1,x2,…,xn，那么xi则表示第i个单目标优化问题的当前解。同时，单目标优化问题对应着权重向量λi，利用权重向量间的欧式距离定义邻居集合，也就是对应权重向量距离最小的子问题集合。

3 MOEA/D算法的改进策略

由于传统的MOEA/D算法在整个进化过程中会保持固定的邻域值和变异概率，容易出现全局搜索能力差和收敛慢的问题，本文提出了自适应的调整策略。同时，构造了双曲线聚合函数，根据权重向量与坐标轴的距离调整个体的支配范围来增强算法的收敛性和散布性。

3.1 双曲线聚合函数

令理想的参考点z*=(0,0,…,0)，在二维目标空间，本文构造了双曲线函数对多目标问题进行分解，表示为

(14)

式中：α表示双曲线的实轴长度，用来调节弯曲度；θ表示双曲线渐近线斜率的倒数，用来调节张角；ki则表示权重向量λ与目标空间上各坐标轴夹角的余弦；f′1,f′2分别表示目标向量f1,f2的变换，表示为

(15)

通过调整参数α和θ能够生成不同形状的曲线，实现对聚合函数的光滑化处理。其中，α可以控制算法的收敛性，而θ可以控制算法的散布性。不失一般性，在处理m维的多目标优化问题时，聚合函数表示为

(16)

从目标向量(f1,f2,…,fm)到(f′1,f′2,…,f′m)的变换表示如下

(17)

式中：A为m×m的变换矩阵，表示为

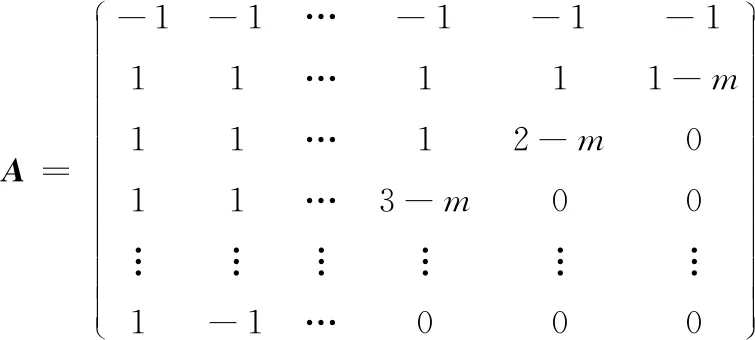
利用双曲线函数对多目标问题进行分解，在选择个体时，使得接近坐标轴的权重向量增大了个体的支配范围，从而具有更强的收敛性。同时，使得距离坐标轴较远的权重向量能够缩小个体的支配范围，则突出了散布性。

3.2 自适应因子调整策略

在多目标优化算法的迭代前期，需要尽量保持种群的多样性，让搜索范围尽可能大些，这样可避免陷入局部最优，而在迭代的后期，则需要提高算法的收敛速度。

3.2.1 自适应变异概率

在MOEA/D算法中大多设置了固定的变异概率，若取值过小会难于产生新个体，影响进化速度，取值过大，则会趋于随机搜索，不仅弱化了全局的搜索能力，还容易出现早熟的问题。为此，提出了一种自适应的变异概率，通过最大适应度与平均适应度的距离来自适应调整变异概率的大小，改进策略描述如下

(18)

式中：fav表示种群的平均适应度值；fmax则表示最大适应度值；k表示范围在(0,1]的常数。当arcsin(fav/fmax)大于等于π/6时，说明种群适应度的平均值与最大值的距离较近，而距离最小值较远，种群的适应度值较分散，个体间的差异明显，种群表现出了多样性，所以此时会相应地降低变异概率值，避免优良个体被破坏，从而提高收敛速度；相反，当arcsin(fav/fmax)小于π/6时，说明种群的平均适应度与最小值距离较近，个体间的差异不大，所以此时会适当地升高变异概率值，避免陷入局部最优，从而能够提高全局搜索能力。

3.2.2 自适应邻域

在MOEA/D算法中，邻域值越大，可选解的数量就越多，也可以更好地维持种群的多样性，但会占用过多的计算资源，且还会使解偏离Pareto前沿；邻域值越小，虽然算法的收敛性增强了，但会弱化种群的多样性。为此，本文通过引入自适应调整邻域值，来平衡算法在整个进化过程中的多样性与收敛性，提升算法的整体性能，邻域值的自适应表达式如下

(19)

3.3 改进算法流程

改进算法的工作具体步骤描述如下：

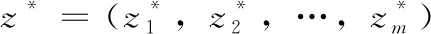
步骤2 遗传操作。计算个体的适应度，再根据式(18)求出变异概率，并进行变异操作得到新个体y，将新个体的适应度值与理想点z的适应度值进行比较和更新；

步骤3 根据当前的迭代进程，利用式(19)计算出邻域值，如y1支配邻域内的y2，则用y1替换y2；

步骤4 若满足收敛条件，则直接输出结果PF；

步骤5 如不满足收敛条件，且未到最大迭代次数，则将迭代次数t+1后，继续执行遗传进化操作。反之，则输出结果PF。

4 改进算法测试验证与对比

为验证本文提出改进算法的性能，在Matlab 2016a环境中进行了测试实验，运行的硬件平台配置为：Intel Core i7的CPU，主频率2.8 GHz；8 GB的内存；操作系统是64位的Windows 7。采用经典MOEA/D、文献[10]中的MOEA/D-DE、文献[11]中MOEA/D-εC、文献[12]中的MOEA/D-DMSM和本文的改进算法求解具有代表性的2维目标空间基准函数ZDT1、ZDT2、ZDT3和ZDT4，每种算法在上述的测试函数上分别运行25次，并将计算得到的反向时代距离(inverted generation distance，IGD)均值和标准差记录到表1中。其中，IGD可以衡量算法的收敛性和多样性，IGD的值越小，则说明计算得到的Pareto最优解的收敛性和分布性越好。设置经典MOEA/D算法参数：采用模拟二进制交叉，ηc=30，交叉率为1，邻域大小T=20。本文提出算法的参数设置如下：双曲线形态调整参数θ=2.8，α=0.12；自适应变异概率的调整参数k=0.75；缩放因子F=0.5。设置种群大小n=100，迭代进化的最大次数tmax=1500。

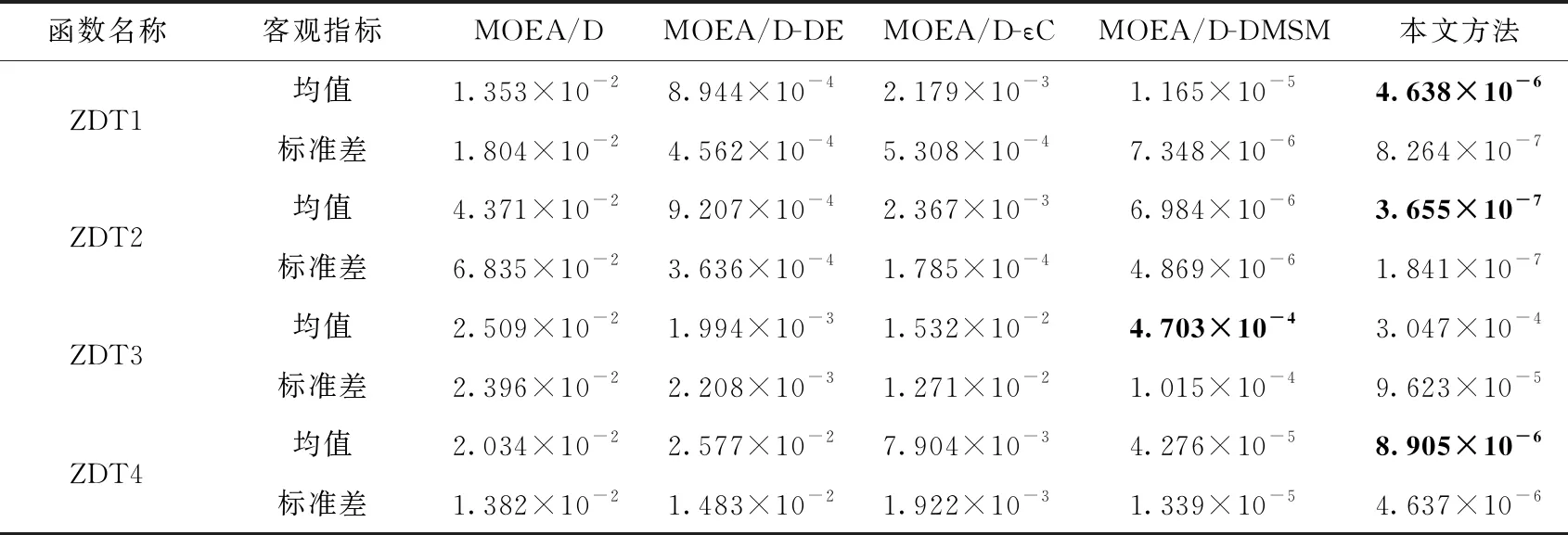
表1 不同算法在测试函数上运行得到的IGD结果

从表1中的数据可直观看出：提出的改进算法在测试函数ZDT1、ZDT2和ZDT4上得到的IGD均值明显优于其它4种比较算法；在测试函数ZDT3上，MOEA/D-DMSM算法得到的IGD均值最优，但与本文提出的改进算法得到的运行结果在同一数量级，且差距并不大，验证了提出的改进方法在改善算法收敛性和多样性方面具有的优势。另外，改进算法计算得到的标准差也都优于其它比较算法，进一步验证了改进策略能够给算法带来更高的稳定性。

为了能够更直观地了解改进算法的运行结果，使用本文的改进算法在测试函数ZDT1-ZDT4上进行求解，得到Pareto前沿的分布情况如图1所示。

从图1的仿真结果可看出：利用本文提出的改进算法在测试函数上得到的非支配解集非常逼近真实的Pareto前沿，且分布较为均匀，从而验证了双曲线聚合函数、自适应变异概率以及动态邻域在进化的不同阶段起到的调节作用，说明了提出改进策略能够有效平衡算法的多样性和收敛速度。

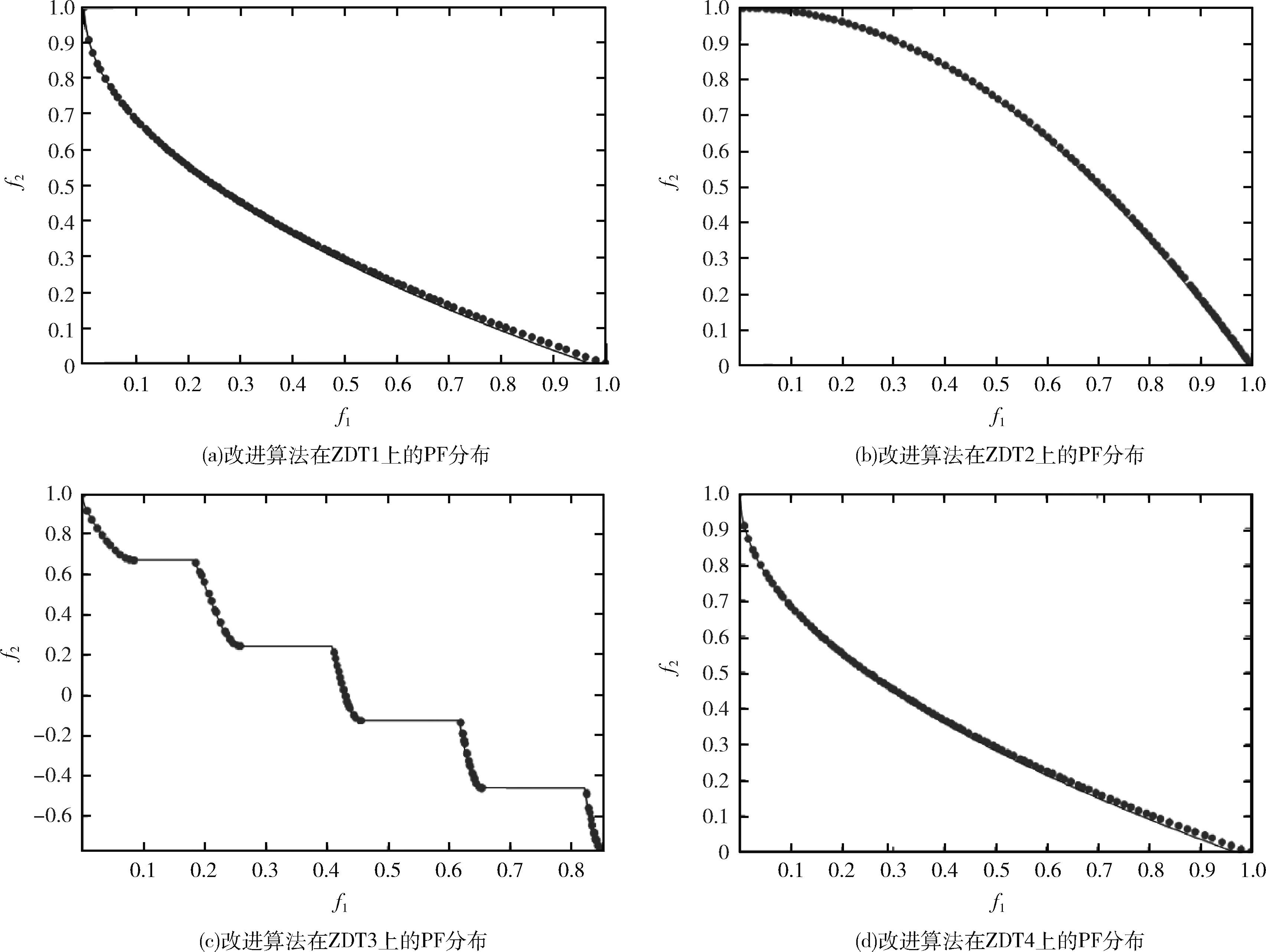
图1 改进算法在测试函数上求解出的PF分布

5 实验结果与分析

为验证本文提出的改进算法在异构网络接入控制中的有效性和优越性，在Matlab环境下进行仿真实验，选择TD-LTE、WLAN和WiMax这3个无线网络组成异构网络，网络配置参数见表2。

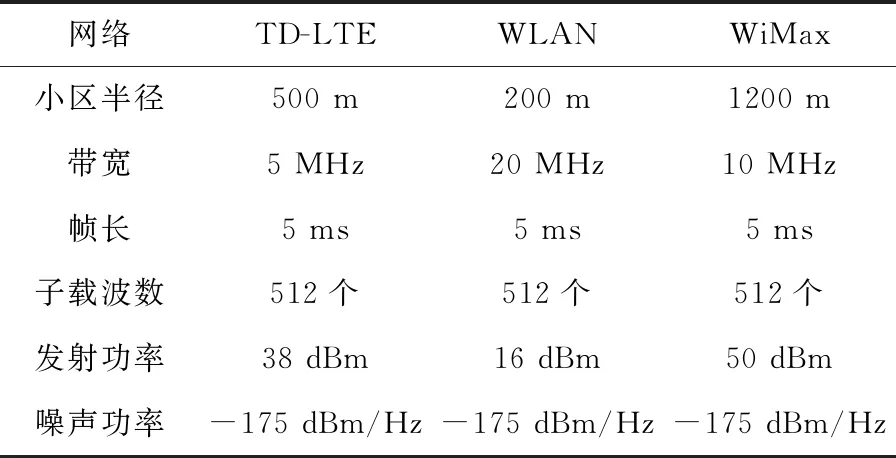
表2 异构网络配置参数

假设异构网络中有50个初始的业务，并随机生成50个待接入的业务，其中实时业务和非实时的业务各占50%，且速率均匀分布在400 kbps-800 kbps和600 kpbs-1200 kpbs。

5.1 不同算法下3种网络归一化负载率对比

为清晰展示3种网络在接入新业务过程中的变化情况，对网络的负载率进行归一化处理，并记录从接入第51个业务到第100个业务在文献[17]、文献[18]和本文改进算法下3种网络归一化负载率的变化情况如图2所示。

从图2的仿真结果可看出：在3种算法下，随着新业务的接入，3种网络的负载率均呈上升趋势。在文献[17]的算法下，由于没有把网络均衡作为优化的目标，在接入相同业务的情况下，3个网络间的负载率相差较大；文献[18]的算法较文献[17]有了较大改善，3条线出现了明显的聚拢，但仍然不够均衡；而在本文改进算法下，3条负载率曲线最紧凑，说明网络负载最均衡，从某种程度上讲，这样能够保证每个网络都有相当的剩余资源供新业务的接入，也能有效避免网络阻塞的情况发生。

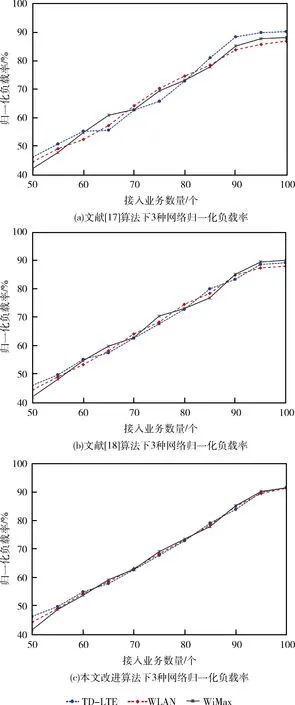
图2 新业务接入过程中归一化负载率变化情况

5.2 不同算法下系统传输速率对比

同样，采用文献[17]、文献[18]和本文改进算法在接入不同数量的新业务时，网络的系统传输速率结果如图3所示。

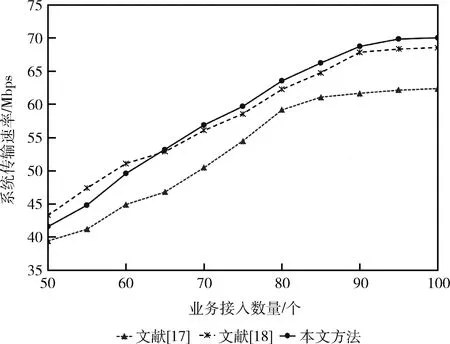
图3 新业务接入过程中传输速率的变化情况

从图3的仿真结果可看出：当接入业务数量小于80个时，在3种算法的作用下，3种网络的传输速率与业务的接入数量呈近似线性增长。由于文献[17]的方法没有考虑负载平衡，且算法求解精度较低，影响了系统的传输速率；而在本文改进方法下，初始状态在所有网络中的系统传输速度为43.5 Mpbs，低于文献[17]，高于文献[18]，但在业务增加过程中，当接入业务数为65时，系统传输速率已变为最大，并一直保持最大的状态，说明提出的改进算法在分配异构网络资源时，能够保证系统的最大的传输速率。

6 结束语

为改善异构无线网络的接入质量，优化异构网络间的负载均衡和系统传输速率，建立了多目标优化模型，然后采用改进的MOEA/D算法进行求解，通过构造双曲线函数对MOP进行分解，并控制权重向量与坐标轴的距离来调整个体的支配范围，同时引入了自适应变异概率和自适应邻域，进一步提高了收敛性和全局搜索能力。在标准测试函数上的仿真结果表明：提出的改进算法得到了更佳的IGD评价指标和Pareto前沿，不仅平衡了算法的多样性和收敛性，而且提升了全局搜索能力。将改进的算法应用在异构网络业务接入控制中，与其它几种算法相比，表现出了更优的性能，不仅有效地平衡了网络间的负载，避免出现网络阻塞，还能保证整个网络系统为终端用户业务提供最大的数据传输带宽，从而验证了改进策略的有效性和优越性。