基于去噪和分形的加密货币投资组合模型优化研究
曹广喜 张星宇
1 南京信息工程大学 管理工程学院,南京,210044 2 南京信息工程大学 滨江学院,无锡,214105 3 南京信息工程大学 气象灾害预报预警与评估协同创新中心,南京,210044
0 引言
加密货币在2008年全球金融危机和互联网技术快速发展的背景下应运而生,是一种不在央行和任何金融机构约束下的“电子货币”,相较于其他货币,具有去中心化交易、匿名性、可审计性等特点[1].加密货币为大众提供了一种新的储值和投资手段,是当下最热门的投资焦点和市场话题之一.然而,加密货币投资的高回报与高风险并存,以受关注度最高的比特币为例,关于它的价格动态的早期研究表明其“极具投机性”[2].因此,研究加密货币投资组合策略对于提高资产风险管理能力具有重要意义.
Markowitz提出的均值-方差(M-V)模型是公认的投资组合理论的开端,然而很多学者认为该模型以方差度量风险存在较大误差[3].于是,VaR、CVaR等[4-5]风险度量手段被相继提出,而CVaR因其突破了正态分布假设的局限,且具有次可加性和凸性[6],被认为是一种比VaR风险计量技术更为合理有效的现代风险管理方法[7-8].虽然这些传统投资组合理论对于现代金融领域发展具有重要意义,但仍然存在应用上的局限性:其一,以方差或CVaR度量风险只在线性假设前提下使用,而越来越多的实证分析证明金融时间序列具有复杂的非线性相依结构[9];其二,金融时间序列由于大量带有时频双域的交易噪声往往呈现不规则和粗糙的结构特征[10],会影响对数据的进一步分析和处理.近年来有研究发现分形方法有利于克服传统模型只能研究序列间线性相依结构的缺陷[11].多重分形消除趋势互相关分析方法(MF-DCCA)是用来分析不同时间标度下两个非平稳时间序列的长期交叉相关性和多重分形性的一种方法,唐勇等[9]将其与M-V模型结合,基于沪港股市组合提出了多重分形投资组合模型,在收益率、波动率、 夏普比率和社会经济福利指标下与传统投资策略进行样本外比较分析,证明了多重分形投资组合模型相对传统线性投资组合模型的优越性.Zhu等[12]在多重分形投资组合模型基础上使用多小波去噪滤除时间序列中的噪声,是对投资组合理论结合分形方法的一次完善.然而Kopsinis等[13]认为与小波去噪法相比,经验模态分解法(EMD)能够自适应地去除噪声,在客观性和分辨率方面更具优势.李合龙等[14]提出了改进的EMD去噪法,通过变点技术判断信噪的分界点,再用软阈值法过滤噪声信号,相较传统EMD方法,这种改进EMD去噪法能兼具变点技术判断含噪信号的精确性以及软阈值去噪的连
续性.尽管国内外对于分形投资组合理论已有一定的研究积累,但是目前这种方法还是仅限于研究较为常规的传统资产,对于波动性更强、流动性更大的“极具投机性”资产——加密货币投资组合的优化效果犹未可知.因此,本研究有助于弥补这一空白.
另外,关于加密货币投资组合的研究起步较晚,且局限在传统投资组合理论框架下.Brauneis等[15]于2019年首次将传统的均值-方差投资组合框架应用于加密货币,并将该框架下的风险和回报与单一市场投资基准相关联,认为加密货币组合化投资可以显著改善投资结果.随后,Liu[16]分析了Bitcoin、Ethereum、Ripple等10种加密货币组成的投资组合也得出了类似的结论.Platanakis等[17]将方差约束条件应用于Black-Litterman模型来构建加密货币投资组合,发现其优于1/N和Markowitz基准,这表明投资者在管理加密货币投资组合时应使用更复杂的投资组合技术,以控制输入参数中的估计误差.
本文借鉴李合龙等[14]提出的改进EMD去噪方法,与分形投资组合模型相结合,提出了EMD-Mean-MF-DCCA模型,解决了以往投资组合模型中金融时间序列时频双域噪声带来的干扰问题.另外,将EMD-Mean-MF-DCCA模型应用于加密货币投资组合研究,证明分形投资组合模型应用于加密货币市场的优越性,是对分形理论应用的一次补充和完善.
1 EMD去噪下多重分形投资组合模型
EMD-Mean-MF-DCCA模型构建的核心是立足于多重分形投资组合模型[9],并融入李合龙等[14]提出的结合变点分析技术和软阈值去噪的改进EMD去噪法.主要通过以下步骤实现:
步骤1.用改进的EMD去噪方法对时间序列X(t)进行去噪处理,得到x(t).具体操作如下:
先对原始序列进行EMD分解,提取本征模函数IMFi(t)和趋势项r(t):
(1)
其中,i=1,2,…,n,n是IMF分量个数.

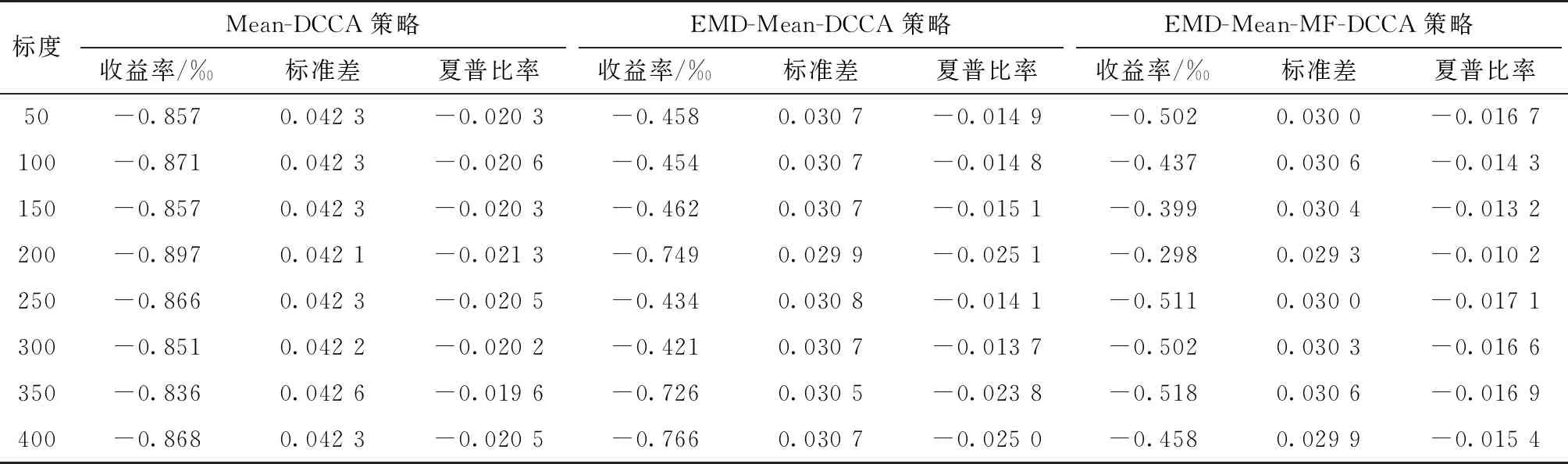
最后,对含噪IMF分量进行软阈值去噪处理,可以获得去噪后的IMF分量,即IMFi(t)′,i (2) IMF1(t)′,IMF2(t)′,…,IMFi0-1(t)′与IMFi0(t),IMFi0+1(t),…,IMFn(t),r(t)加总后得到去噪的重构序列x(t). 步骤2.在MF-DCCA方法的基础上构造EMD-Mean-MF-DCCA模型.具体操作方式如下: 首先,将新序列x(m)(t),t=1,2,…,N,N表示时间序列的长度,代入式(3),构建轮廓序列: (3) (4) 然后,将q阶波动函数定义为 (5) 如果两个时间序列是长程相关的,则标度关系满足Fxy(q,s)~shxy(q).若0 最后,将重构序列及q阶波动函数代入M-V模型,构建EMD-Mean-MF-DCCA: (6) 步骤3.用多目标模糊非线性规划方法(FMNP)[12],来获得满足收益最大、风险最小双重目标的最优权重分配方案.FMNP应用于EMD-Mean-MF-DCCA的算法如下: (7) 其中,f(w),g(w)作为两个目标函数,分别对应的两个隶属函数μf(w),μg(w)如下: (8) (9) 假设λ为最大满意度,即 λ=max{minμf(w),minμg(x)}. (10) 若在步骤2取n个q阶,则每个标度s对应n组(不同q阶下的)权重配置方案.在标度为s0,q=k时,满足λ=max{minμf(w),minμg(w)},得到标度s0下的最优权重配置方案{wi,k,s0}. EMD-Mean-MF-DCCA模型应用于优化资产投资策略的大致路径是:先采用改进的EMD方法滤除金融序列中的噪声,得到滤噪后的重构序列,再结合滚动窗技术,利用MF-DCCA改进下的新模型从不同的波动幅度中提取有效的预测信息,并通过FMNP将其整合到相同的时间尺度中,由此可以得到不同时间尺度下的最优资产配置方案. 本文选取比特币、莱特币、瑞波币这三种有较长发展历史且极具代表性的加密货币作为研究对象,数据样本范围为2013年8月5日至2020年4月21日,一共有2 452组日收盘价数据.数据来自于https:∥coinmarketcap.com/. 2018国际数字经济博览会发布的《区块链3.0共识蓝皮书》提出明确的区块链时代划分,认为区块链产业在2018年进入3.0阶段,在这一阶段,区块链技术将突破其在金融领域的应用范畴,赋能实体经济.随着区块链技术应用范围不断扩大,各国政府逐步将这一新型金融市场纳入监管范围.尽管从长远来看,加强市场监管有利于解决加密货币行业的各种市场乱象,但也促使短期内加密货币市场由牛转熊.由图1—3可知,币价在区块链2.0时代末期飞涨后,于区块链3.0时代迎来大幅崩溃.其中比特币在2017年12月16日达到了历史新高的19 475.8美元,随后开始急剧下跌,其他加密货币也在1个月之内对其价格暴跌做出了回应[19]. 图1 比特币价格走势Fig.1 Bitcoin prices during Aug.5th,2013 to Apr.21st,2020 图2 莱特币价格走势Fig.2 Litecoin prices during Aug.5th,2013 to Apr.21st,2020 图3 瑞波币价格走势Fig.3 Ripple prices during Aug.5th,2013 to Apr.21st,2020 取对数收益率可以有效消除币价的指数趋势,因此加密货币的日收益率定义为:Ri(t)=ln(Pi(t))-ln(Pi(t-1)),其中Pi(t)表示加密货币i在t交易日的收盘价.表1显示,三个序列的偏度大于0,表现为右偏特征,峰度均大于3,表现为显著的尖峰厚尾特征,J-B统计量显著,表明收益率序列不服从标准的正态分布.ADF单位根检验结果表明各个序列在1%水平下皆拒绝原假设,经过差分后的各个序列已经平稳.三个Hurst指数均小于0.5,显示加密货币时间序列具有反持久性,说明选取的资产序列均服从有偏随机游走过程. 表1 收益率的描述性统计 投资组合模型效果比较一般通过样本外检验实现[21].所以本文将基于滚动窗口技术进行样本外检验,分析EMD-Mean-MF-DCCA是否优于其他比较模型.按照2.1提到的时代节点将区块链2.0时代2013年8月5日至2017年12月31日划分为估计样本区间,长度为1 610个交易日;区块链3.0时代2018年1月1日到2020年4月21日划分为预测样本区间,长度为842个交易日.本研究遵循追求最小风险的原则,将始终依次选取1 610个观察值作为滚动窗口,采用m=3阶的最小二乘法对窗口区间的局部趋势进行拟合,在给定期望收益条件下风险最小的组合点构成的投资组合有效前沿上,选择有效前沿上的最小方差组合作为观察值外下一个交易日的最佳资产配置方案,然后不断迭代直至得出整个预测样本区间一共842个交易日的最优资产组合配置方案.根据估计窗口长度,标度s的取值为50、100、150、200、250、300、350、400,q阶取-2、-1、1、2、3、4. 对照基准包括单一市场投资策略、等权重策略、Markowitz策略、Mean-CVaR策略(置信水平选取90%、95%)[8]等传统投资组合策略.策略评价指标选取收益率、标准差和夏普比率,其中夏普比率为[E(Rp)-Rf]/σp.E(Rp)-Rf指超过整个样本期的无风险收益率的平均投资组合收益,Rf是无风险利率,本文假设其为0,σp是在样本期间预测的投资组合标准差. 由表2可知,单一投资比特币的策略在收益、风险、夏普比率方面均要优于其他对照组.可以看出比特币作为最早发行的加密货币,在区块链3.0时代下,不论从收益率角度来看,还是从风险的角度看,相比于其他加密货币都具有绝对的优势.实际上,比特币自发行之日起,就一直占据绝对的市场支配地位,体现在:其一,比特币的市场占比自始至终领先于其他加密货币,即使是价格在2017年12月大幅崩溃,其市场占有率最低也达到了32.81%,在整体加密货币中排名第一,随后在2019年占比最高升至69.90%;其二,比特币的流动性远大于其他加密货币.有调查表明,比特币的流动性似乎是以太坊的5倍,是EOS、Litecoin、XRP和BCH等其他所有加密货币的 10 倍以上.由此可见,比特币单一市场作为最优基准有理可依. 表2 对照基准样本外检验结果 由表3可知:Mean-DCCA策略在收益率上有4组优于或等同于比特币单一市场投资策略;有7组风险小于或等同于比特币单一市场投资基准;4组的夏普比率优于或等同于比特币基准.由此可以看出,单分形投资组合模型通过刻画和描述加密货币市场在不同时间标度下的波动[12],从看似无序的市场结构中描述其运行规律,提高了投资组合的盈利能力和抗风险能力.整体来看,在时间标度s=350时,收益率和夏普比率这两个指标要优于其他标度组,s=200时,标准差要小于其他标度组.而叠加改进的EMD去噪方法得到EMD-Mean-DCCA策略后,发现任意标度下相对Mean-DCCA策略,在提高收益率和降低风险方面均取得了显著的成果.可以证明改进的EMD去噪方法能够有效地过滤时间序列的噪声,起到优化分形投资组合的作用.另外,在去噪条件下,标度s=300时,投资组合的收益率和夏普比率最大,s=200时,风险最小.至于EMD-Mean-MF-DCCA策略,从表3中可以看出,该策略在任意标度下从收益、风险和夏普比率三个方面均优于单一投资比特币的策略,且明显优于同标度的Mean-DCCA策略.而相较于EMD-Mean-DCCA策略的优势主要体现在降低风险的效果上.其中,时间标度s=200策略下的收益率和夏普比率要优于其他任何基准,同时该策略的标准差小于其他基准.可见与其他模型相比, EMD-Mean-MF-DCCA模型可以有效消除时间序列中的噪声,并整合来自不同波动的预测信息,以达到改善投资组合的绩效的目的,从而可以为不同交易周期的投资者们提供盈利能力和抗风险能力更佳的投资策略.综合比较上述基准,发现使用分形和去噪方法构建的投资组合模型能够取得良好的投资组合效果,优于单一市场、M-V等传统投资组合策略.其中EMD-Mean-DCCA是EMD-Mean-MF-DCCA的特殊形式,即仅考虑波动幅度q=2的情况.整体来看,EMD-Mean-MF-DCCA策略下的最优时间标度为s=200,EMD-Mean-DCCA策略下的最优时间标度为s=300,而加密货币市场进行短期投资或者长期投资则难以取得最佳的投资效果,投资者进行短期投资可以及时根据市场行情来调整投资组合权重,纵然有机会减少极端事件对投资组合的影响,但是对于极具投机性的加密货币来说,难免效率低下.另外,自2017年数字货币暴涨以后,加密货币市场兴起了“屯币”行为,随之而来的就是数字货币一再的大幅崩溃,导致很多投资者被2017年巅峰时期投资的数字货币套牢,结合实证结果,认为长期持有加密货币需谨慎. 表3 分形投资组合策略样本外检验结果 稳健性检验部分将调整估计样本区间取值范围,讨论加密货币价格处于上升趋势时使用EMD-Mean-MF-DCCA模型是否仍然具有优势.由图1—3可以看出比特币价格约在2019年1月底开始有所回升(第2 000组数据),到同年9月底又开始下降,其他加密货币也随之产生波动.故该部分以总样本前2 000组数据作为估计样本区间,后452组数据作为预测样本区间. 由表4—5可知,改进模型的优化效果在收益率和夏普比率这两个指标上的表现与前文描述差异不大,但是在标准差这一指标上表现不佳.其次,依次改进的三种模型均是s=300的标度组表现最为优异,这也验证了分形方法下的加密货币组合进行短期投资或者长期投资均不能取得最优的投资效果.另外,EMD去噪方法下分形投资组合模型的收益率和夏普比率要优于未去噪的加密货币投资组合模型,可见叠加去噪方法对分形投资组合起到了优化作用.通过稳健性检验可以发现,无论加密货币价格面对上升趋势还是下降趋势,EMD-Mean-MF-DCCA模型相较于其他基准均具有优势. 表4 对照基准样本外检验结果 本文结合EMD去噪法和分形方法在均值-方差模型的基础上进行模型的优化研究,提出了新模型EMD-Mean-MF-DCCA,并以比特币、瑞波币、莱特币为研究对象进行加密货币投资组合策略比较分析.通过样本外检验和稳健性检验,主要结论如下: 1)研究发现单独利用单分形方法以改进M-V模型,即能取得显著的优化效果,且多分形投资策略要优于单分形投资策略,验证了用分形方法改进M-V模型中风险度量手段的优越性. 2)新模型EMD-Mean-MF-DCCA通过改进风险度量手段和剥离时间序列自身的含噪信号,解决了传统均值-方差模型实际应用的两个缺陷.经过实证检验,发现去噪多重分形投资组合策略优于单一市场、等权重、M-V和Mean-CVaR等传统投资组合策略,也要优于单分形投资组合策略和去噪单分形投资组合策略.其优越性具体表现为,无论数字货币价格正处于上升趋势还是下降趋势,新模型相较于其他基准均在盈利能力和夏普比率方面具有优势;另外,当数字货币大幅下行震荡时,新模型下的组合投资方案还具有较好的抵抗风险能力. 虽然本文验证了EMD-Mean-MF-DCCA策略相对于其他传统投资组合策略在提高收益、分散风险上的优势,但是最优时间标度会受波动幅度信息、估计样本区间的影响.无论去噪分形投资组合模型改进程度如何、无论当前的加密货币价格趋势如何,对加密货币投资组合而言,短期投资或者长期投资均难以取得最佳的投资效果,而如何在投资前确定最佳的交易周期仍有待进一步研究. 表5 分形投资组合策略样本外检验结果


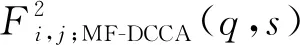
2 实证分析
2.1 数据选取与描述性统计



2.2 投资组合样本外检验分析

2.3 稳健性检验

3 结语


