基于小位移旋量的旋翼系统公差建模及分析

刘壮壮，韩东

（南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京210016）

0 引 言

机械加工精度在很大程度上影响着工艺装配体的整体性能，在工程实践中须慎重考虑。如果考虑不周，可能会导致结构的磨损疲劳、振动破坏等问题。直升机的振动问题与加工制造技术有着紧密联系。若制造装配工艺不达标，就会造成各片桨叶对旋翼中心的质心和质量静矩不平衡、相邻桨叶夹角不相同等旋翼质量不平衡问题，以及各片桨叶的扭转刚度不相同，进而带来旋翼气动不平衡等问题。为了降低直升机的振动水平，对旋翼系统的三维公差进行建模分析也非常有必要。

目前，在零件三维公差建模分析方面，国内外采用的主要方法包括T-Map法［1-2］、雅可比旋量法［3-5］以及小位移旋量（SDT）法［6-8］等。这些方法均是把零件看作刚体，利用几何误差累计进行模型精度求解。T-Map法的计算精度较高，以基于公差域的边界及变动要素进行公差建模，以所有符合公差要求的点的集合来对各类误差特征进行计算，然而使用T-Map法难以描述零件间误差的作用关系及其分布情况［6］。雅可比旋量法将雅可比方法和旋量方法相结合对公差进行数学建模，可同时处理尺寸公差、几何公差。雅可比方法是以点集的形式表示微小位移，以机器人刚体运动学变换理论来表征开环链路上的微小位移；旋量法是采用小角度假设，以受约束的旋转矢量来表征微小变动量；雅可比旋量法算法简洁，但变换矩阵规模不一，可移植性不强。

小位移旋量（SDT）法是把表征实际特征与理想特征之间的误差用小位移旋转矢量的方法表示出来，然后基于误差传递的误差累计进行计算。任何零件的几何特征可用点和法线矢量表示。采用小位移旋量法，即将一个理想表面的几何特征位置相对于另一理想表面的几何特征位置的刚体运动用六个运动分量精确表示，即三个平动矢量和三个转动矢量。吴兆强［9］研究了小位移旋量的公差建模方法，结合齐次坐标变换理论完成了对装配路径上的公差建模分析，并通过实例验证了该 方 法 的 可 行 性；J.N.Asante［10］将 累 计 的 误 差 用小位移旋量参数进行表示，并通过公差模型的求解计算获得零件的加工特征边界；吕程等［8］利用小位移旋量理论，结合蒙特卡罗与响应面相结合的圆柱度公差建模分析方法，验证了该方法在提高机床精度设计时的实用性；S.Jin等［11］将小位移旋量法应用于圆锥模型的公差求解，提出一种圆锥表面及其公差模型的表示方法，并通过实例获得统计分析结果；孙岩辉等［6］利用零部件间的约束定位关系，采用小位移旋量及齐次坐标变换相结合的方法，统计分析了主轴几何回转精度的问题；黄康等［12］将小位移旋量和响应面法相结合，建立了齿轮的公差模型求解方法，并通过实例分析证明了该方法具有较高的精度。虽然国内外在小位移旋量法的理论及实例分析方面均做了大量研究，但是将其应用于直升机方面却鲜有报道。

随着直升机技术的不断发展，对现代直升机的性能在各方面都有了更高的要求。为了能有效降低直升机的振动，有必要从降低制造误差方面进行建模分析。本文通过旋翼传动系统模型，依据小位移旋量（SDT）的公差建模，结合齐次坐标逐次变换公差累计分析［13］，对旋翼上各个桨叶在旋转时的几何回转精度进行计算。

1 旋翼公差模型的建立及分析

1.1 旋翼系统模型的建立

本文研究旋翼系统几何回转精度计算，即单个桨叶的根部安装位置在整个旋翼系统空间的变动情况。本文所建立的旋翼系统模型包括传动—变速齿轮组、行星减速器齿轮系统，旋翼轴，桨毂架，变距、挥舞、摆振铰，如图1所示。其中，行星减速器齿轮系统根据文献［14-15］所建，其余均根据旋翼特性而建。对于旋翼系统，从传动变速齿轮组到行星减速器，再到旋翼轴、桨叶根部就是一个完整的链路。计算该路径上的模型公差得到的回转误差即是旋翼系统的旋转精度。

图1 旋翼传动系统模型Fig.1 Rotor drive system model

所建模型采用小位移旋量法进行公差建模。对于零件本身，在加工制造中必然存在加工精度问题。即零件本身存在的形状尺寸误差和配合表面形位误差，导致相邻元件间的实际配合表面与名义配合表面存在偏差。实际配合表面相对于名义配合表面的空间位置变动量即为系统的精度误差值。对于旋翼系统，采用随机模拟的方法，用齐次坐标转换矩阵表征实际配合表面相对于名义配合表面的误差值，并沿着装配链路将所有相邻元件的配合表面误差进行累计，获得装配链路上的误差变动范围。

1.2 小位移旋量的公差建模

小位移旋量（SDT）法将刚体的运动用六个运动分量表示，可以用来表征理想形状物体各个方向上的运动，即可以实现刚体间配合表面的偏离运动。

对于实际的机械加工产品，其加工表面是一个与理想表面存在偏差的特征表面。任何零件的几何特征可用点和法线矢量表示。而几何特征的变动量又可以用三个平动矢量和三个转动矢量精确表示。采用小位移旋转矢量法，即表示一个理想表面S2的几何特征相对于另一理想表面S1的几何特征位置的坐标变换，如图2所示。

图2 理想表面S2相对于S1的几何特征位置坐标变换示意图Fig.2 Schematic diagram of the coordinate transformation of the geometric feature position of the ideal surface S2 relative to S1

S1X1Y1Z1、S2X2Y2Z2分别表示理想表面S1、S2的几何特征坐标系。小位移旋量D由旋转矢量ρ和平移矢量ε这两组矢量组成［9］，即

式中：α、β、γ为单位旋转矢量在局部坐标系x、y、z轴上的投影；u、v、w为单位平移矢量在局部坐标系轴上的投影。

通过机器人运动学坐标变换理论，将公差模型表示成4×4的齐次坐标变换矩阵（Homogeneors Transformation Matrix，简称HTM）形式T［9，13］：

P点坐标位置由坐标系S2X2Y2Z2转换到S1X1Y1Z1下的转换关系为

在误差计算模型中主要存在两种公差，一是尺寸公差，二是形位公差。对尺寸公差的影响可以假定所有零件为刚体。对于零件本身，尺寸公差只影响其端面的法向位移或柱面的同轴膨胀，不存在小角度假设问题。因此同样可以采用小位移法将尺寸公差转换成齐次变换矩阵进行累计计算。对形位公差，常见的公差类型有形状公差（如直线度、平面度、圆度等），定向公差（如垂直度、倾斜度、平行度等），定位公差（如同轴度、对称度、位置度等）三类。形位公差变动类型及所建模型的样例如表1所示。

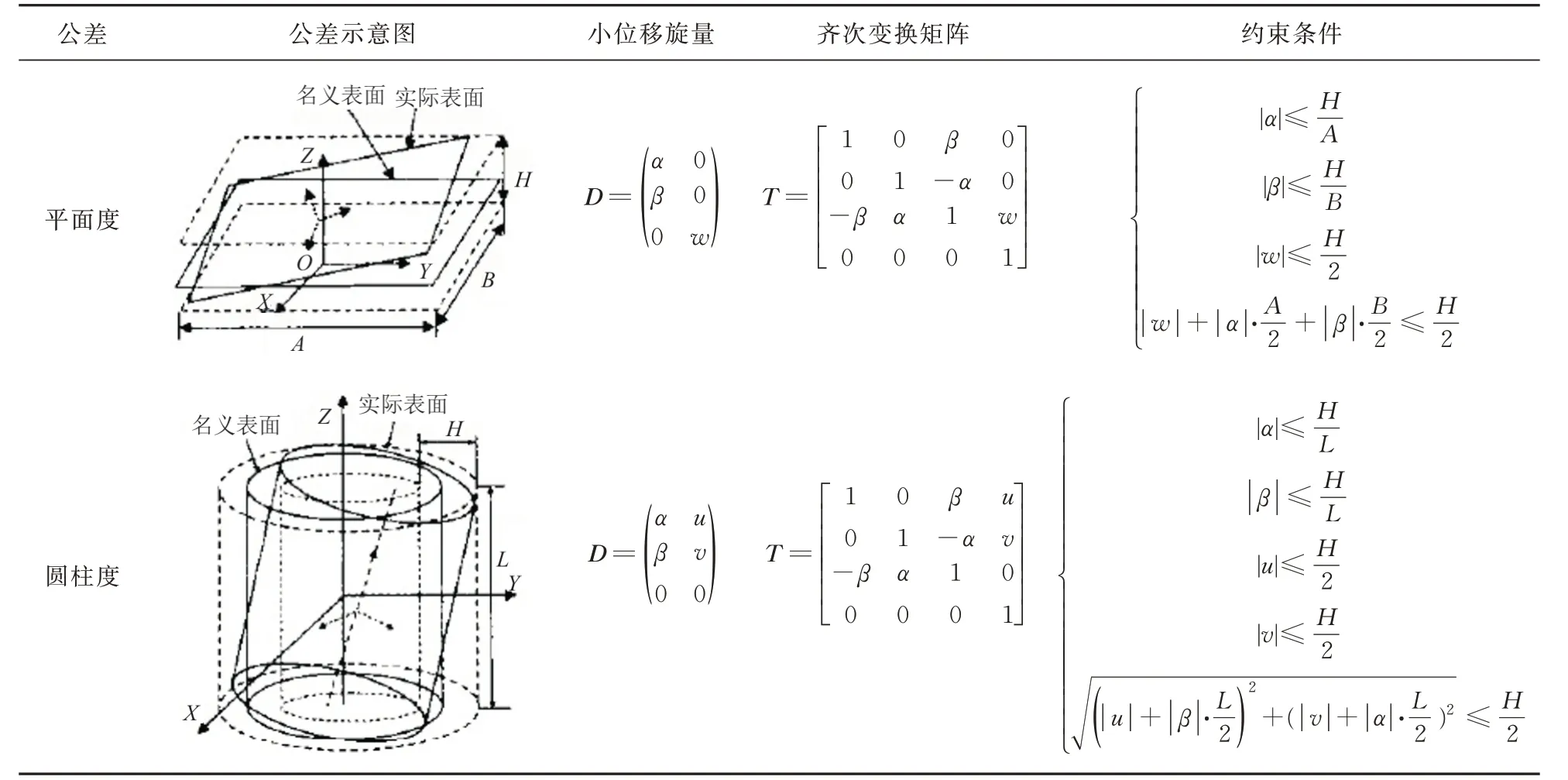
表1 形位公差建模［9］Table 1 Geometric tolerance modeling［9］

1.3 齐次坐标逐次变换分析

齐次坐标是用n+1维坐标来描述n维坐标的向量，在数学表达中用齐次坐标变换矩阵可以很方便地将一个齐次坐标从一个空间坐标系映射到另一个空间坐标系。在零件间配合面处分别建立名义配合表面几何特征坐标系和实际配合表面几何特征坐标系，如图3所示，运用齐次坐标变换矩阵可以将测量点P从名义坐标系下的位置坐标转换成实际坐标系下的位置坐标，实现测量点P从一个空间坐标系到另一个空间坐标系的映射。其中O i为名义特征表面坐标系，O ii为实际特征表面坐标系。

图3 装配体公差传递路径Fig.3 Assembly tolerance transmission path

装配体中任一配合表面从名义特征坐标系转换到实际特征坐标系都会影响后续零件在全局坐标系内的空间姿态。对于测量点P来说，其在全局坐标系下的空间位姿会受到装配路径上各个环节配合表面变动的多重影响。其数学描述为用传递路径上所有相邻坐标系间变换矩阵串联形式的叉乘。则测量点P的空间变动为实际配合下的全局坐标与名义配合下的全局坐标的差值。

式中：T11、T22和T33为零件P1、P2和P3之间实际配合表面相对于名义配合表面的坐标变换矩阵；T12和T23为零件P1到P2和P2到P3之间名义坐标相对变化矩阵。

2 基于小位移旋量的公差建模方法验证

为了验证小位移旋量的公差建模方法，对液力变矩器泵轮毂（如图4所示）进行公差建模。由于液力变矩器的叶窝外形难以用数学描述，仅将液力变矩器的泵轮毂作为研究对象。张海宁等［16］中给出了泵轮毂轴的径向圆跳动公差值、外径公差带、轴向尺寸公差值实验测量数据，如表2所示。

表2 实验测量数据Table 2 Experimental measurement data

图4 液力变矩器泵轮毂简图［16］Fig.4 Schematic diagram of the hydraulic torque converter pump hub［16］

采用小位移旋量的公差建模方法，计算液力变矩器泵轮毂轴的各个对应公差值。首先在泵轮毂一端建立全局坐标系（如图4所示）。由于基本尺寸不影响公差建模，设定泵轮毂外径尺寸为a，轴向尺寸为b。根据文献［16］测量范围标定理论公差值如图4所示。在泵轮毂轴侧表面及端面取任一点M、N作为待测点。结合小位移旋量公差理论，计算得到的力变矩器泵轮毂轴的径向圆跳动公差值、外径公差值、轴向尺寸公差值如图5～图7所示，并对每种公差类型进行4组模拟仿真。

图5 径向跳动公差值仿真与实验结果Fig.5 Simulation and experimental results of radial runout tolerance

图6 泵轮毂外径公差值仿真与实验结果Fig.6 Simulation and experimental results of the tolerance value of the outer diameter of the pump hub

图7 轴向尺寸公差值仿真与实验结果Fig.7 Axial dimensional tolerance value simulation and experimental results

从图5～图7可以看出：仿真结果公差数据围绕实验测量数据波动，且所有数据均满足在要求的测量范围内。

3 旋翼公差模型的实例分析与仿真

3.1 旋翼公差模型的实例分析与计算

将行星减速器齿轮系统、旋翼、桨毂架以及变距、挥舞、摆振铰作为一个完整链路计算旋翼的旋转精度。首先对装配路径上的零件及零件与零件的配合表面处分别建立如图8所示的坐标系，定义O0x0y0z0为全局坐标系，建立在变速传动齿轮下底面旋转中心位置处；局部坐标系O1x1y1z1建立在太阳轮上表面的旋转中心处；局部坐标系O2x2y2z2建立在与行星架连接位置处的旋翼轴端面形心处；局部坐标系O3x3y3z3建立在桨毂架底座上表面的形心位置处；局部坐标系O4x4y4z4建立在挥舞铰连接件孔的形心位置处。

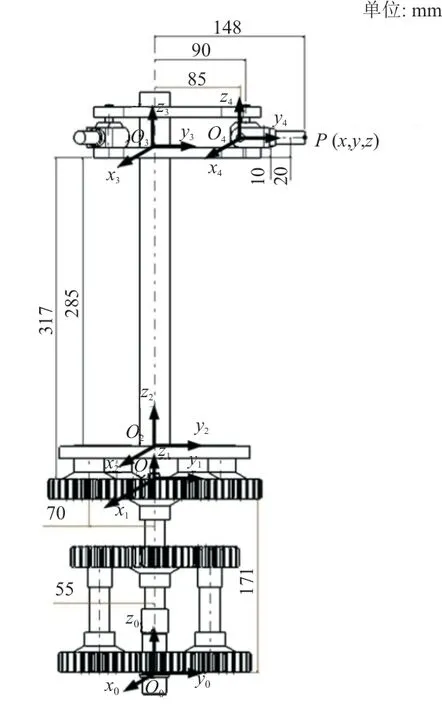
图8 旋翼传动系统模型Fig.8 Rotor drive system model

待测点P在局部坐标系O4x4y4z4下的齐次坐标表示为P局部=[0 63 0 1]T。

求解名义装配下P点的全局坐标位置点。由全局坐标系O0x0y0z0到局部坐标系O1x1y1z1只需要z方向的平移得到。则相应的小位移旋量及齐次变换矩阵表示为

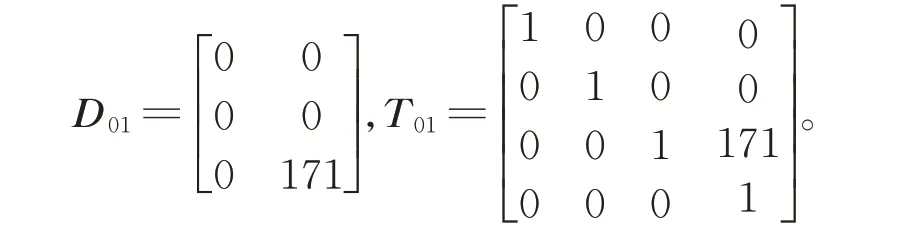
同理，可得相邻局部坐标系O1x1y1z1、O2x2y2z2、O3x3y3z3及O4x4y4z4之间的齐次坐标变换矩阵T12、T23、T34。则名义装配下P点的全局坐标为

对实际装配下的模型进行误差建模并求解实际装配下P点的全局坐标。首先对本文的模型进行误差分析。

对小位移旋量D中的参数进行统一编号表示：(αi，βi，γi，ui，v i，w i)，下标i代表第i种公差类型产生的误差值。则本文所建模型在误差传递路径上具体存在的关键公差类型及相应的齐次坐标变换矩阵如表3所示。

表3 对零部件装配路径上的关键公差进行建模Table 3 Modeling the key tolerances on the component assembly path

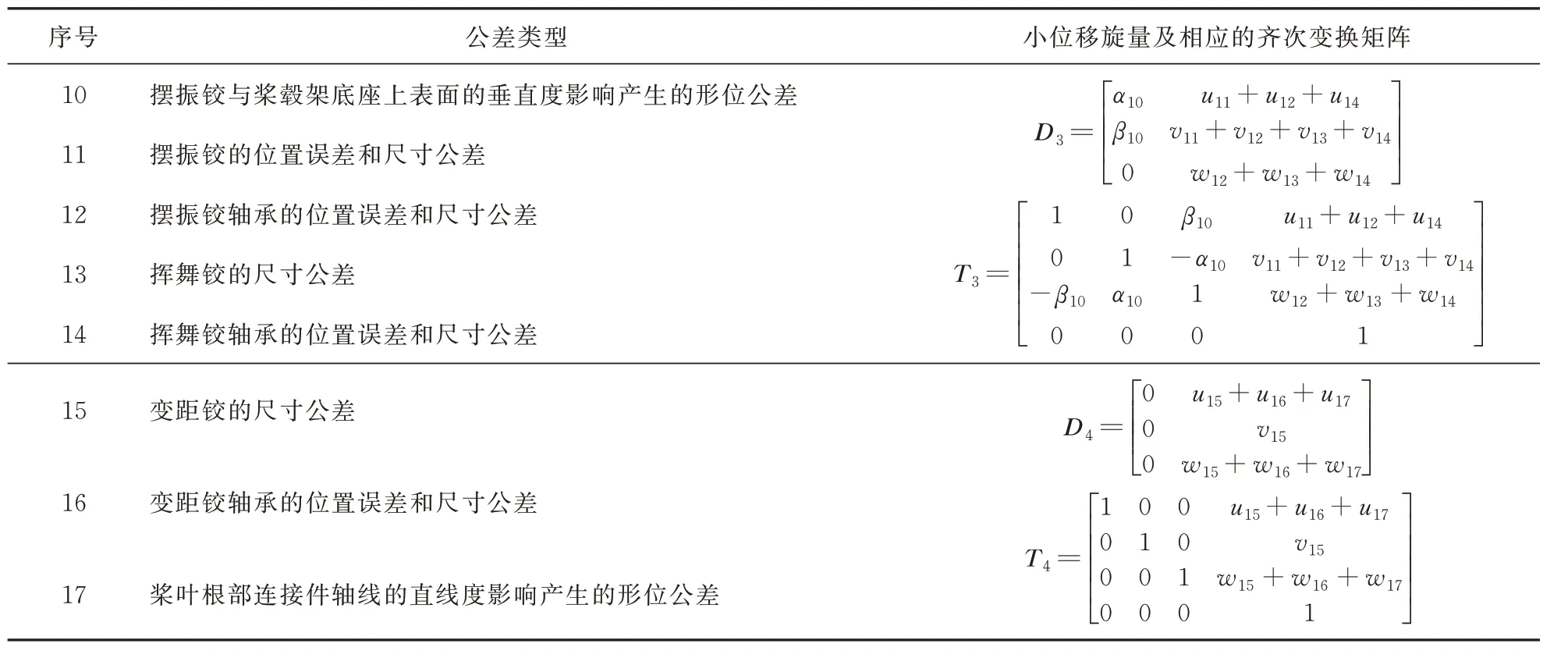
续表

实际装配下P点的全局坐标为

根据装配路径，求解P点相对于全局坐标系的变动范围：

3.2 采用蒙特卡洛仿真对公差模型进行分析

采用蒙特卡洛法对旋翼系统旋转精度进行仿真分析，具体流程如图9所示。

图9 旋翼传动系统装配精度分析流程Fig.9 Assembly accuracy analysis process of the rotor drive system

通过随机误差取值，模拟配合表面的空间变动情况。名义配合表面相对于实际配合表面的随机误差取值以满足各个形位误差和尺寸误差的约束方程有效。

对于尺寸公差，其公差域围绕x、y、z轴三个方向的平动，约束方程为

式中：ui、v i、w i为三个方向的实际尺寸公差；H为理论尺寸公差。

对于形位公差，根据不同的形位公差变动类型有不同的约束条件。在平面配合中，其平面度公差域围绕x、y轴的转动和z方向的平动，约束方程为

式中：αi、βi、w i为实际形位公差；A、B为装配平面x、y方向特征长度；H为理论形位公差。

对旋翼系统传动公差模型进行12 000次随机模拟，得到P点相对于名义全局坐标的空间变动范围，如图10所示，可以看出：在x方向P点的变动范围为-0.430 992到0.423 266，在y方向的变动范围为-0.440 133到0.414 551，在z方向的变动范围为-0.659 146到0.663 532，分别如图10～图13所示。

图10 测量点P在全局坐标系下的空间变动范围Fig.10 Spatial variation range of measuring point P in the global coordinate system

图12 测量点P在全局坐标系下的y向变动范围Fig.12 Range of y-direction variation of measuring point P in the global coordinate system

图13 测量点P在全局坐标系下的z向变动范围Fig.13 Range of z-direction variation of measuring point P in the global coordinate system

从图10可以看出：P点在全局坐标系下的空间变动范围近似呈现为一种椭球形。

从图11～图13可以看出：测量点P在x、y方向的误差限接近，其波动差值为0.854 684，所占误差百分比约为0.58%，而在z方向的误差限较大些，波动差值为1.322 678，所占误差百分比约为0.89%。

图11 测量点P在全局坐标系下的x向变动范围Fig.11 Range of x-direction variation of measuring point P in the global coordinate system

旋翼系统上的桨叶在旋转一周过程中的波动情况如图14所示，可以看出：旋翼桨根部位呈现高度复杂的波浪运动。

图14 旋翼上的桨叶在旋转一周过程中的波动情况Fig.14 Fluctuation of the blades on the rotor during one revolution

4 结 论

（1）本文依据小位移旋量的公差模型及齐次坐标变换的方法可以近似精确模拟旋翼桨叶在桨盘平面内及垂直桨盘平面的波动情况。

（2）通过对旋翼系统的公差模型分析可知，旋翼桨叶根部存在复杂的三维波动情况。其空间变动范围近似呈现为一种椭球形，这与旋翼自身的结构对称性相对应。

（3）通过误差限的精确计算，有利于工程实践中更精确地了解旋翼桨叶振动的干扰因素，并提高对不合格设计结果的改进效率。