几何随机分布模型的高速铁路山地信道建模
李翠然,季一凡,吕安琪,段宝峰
(兰州交通大学 电子与信息工程学院,兰州 730070)
0 引 言
高速列车运行速度快、经历的地形(如高架桥、路堑、隧道和山地等)复杂多变。山地作为一种常见的高铁地形,大量分布于我国西南和西北地区,例如,成贵高铁沿线就穿越了大量的山地、隧道等。与其他地形相比,山地场景下的无线信号传播有其自身的特点,该场景中除了列车周围存在建筑物或树木等散射体外,远端的山体同样会对信号产生反射和散射。因此,在中国高铁迅速发展的研究背景下,建立合理、准确的山地地形信道模型是十分必要的。
目前,只有少量文献针对山地地形的无线信号传输进行了测量与建模研究[1-3]。信道模型的构建主要基于部分测量数据,缺乏一定的普适性。文献[4]采用射线跟踪法对户外场景和隧道内的无线信号传播特性进行了建模研究,该模型计算复杂度较高,实现困难。文献[5]基于随机传播图理论构建了髙铁无线信道仿真模型,虽然模型简单,但其预测精度较低。文献[6-8]针对开放空间、高架桥和路堑场景,构建了几何随机分布模型(geometry-based stochastic model, GBSM),假设散射体分布于以基站和移动台为焦点的多重共焦椭圆上。文献[9-10]引入了单环模型和椭圆模型,对高速铁路场景中的近、远端散射体进行了有效区分。然而,上述信道模型均基于如下假设,即来自基站的无线电波仅从单一平面传播至移动台,该假设条件对于地势起伏较大的山地地形来说,显然是不合理的。由此,学者们针对高铁场景下的三维(3D)信道建模问题展开了研究。
文献[11]以郊区和城市环境为研究场景,构建了球形多输入多输出(multiple-input multiple-output, MIMO)信道模型,并对比分析了不同场景的空间相关性。文献[12-13]分别针对深沟堑场景和隧道场景提出了一种基于3D圆柱的几何随机模型,研究了收发端天线距离和仰角对空时相关特性的影响。文献[14]考虑了角度参数的时变性,将高架桥、路堑和开阔地场景下的2D多椭圆GBSM模型拓展到了3D。与2D模型不同的是,3D模型中考虑了散射体相对于基站和移动台的仰角。然而,上述信道建模方法并未区分近、远端散射体。在高铁山地场景中,近、远端散射体对无线信号的反射和散射作用是不尽相同的,会影响3D MIMO信道建模的精确性和通用性。
针对上述缺陷,本文研究了高铁山地场景下的3D MIMO无线信道建模问题。
1 山地场景的3D GBSM模型
高铁山地场景下,由于铁路沿线的建筑物、树木以及远端的山体对无线信号的反射及散射作用,移动台接收信号是来自直射路径和近、远端散射体产生的大量非直射路径的合成信号。典型的高铁山地地形见图1。
MIMO技术作为4G LTE的关键技术之一,能够在不增加系统带宽需求的条件下改善传输可靠性[15]。本节以山地场景中下行链路2×2MIMO信道为研究对象,展开3D GBSM建模分析。图2为考虑了视距(line of sight, LoS)和单次反射(single bounced, SB)路径的3D GBSM模型。图2中,由于基站作为发射端、移动台作为接收端,以移动台为中心、R为半径的球面上分布着的散射体称为近端散射体,以基站和移动台为焦点的椭圆体上分布着的散射体称为远端散射体。近端散射体S(n1)(n1=1,2, …,N1)和远端散射体S(n2)(n2=1,2, …,N2)的数目分别为N1,N2。表1为3D GBSM模型的相关参数含义。

图2 山地场景的3D GBSM模型Fig.2 3D GBSM model for mountain scenario

表1 3D GBSM模型中的参数Tab.1 Parameters in 3D GBSM model
考虑到信号经过多次反射后功率会大大降低,且不同反射路径反映了相同的信道统计特性[11]。因此,为降低GBSM模型的复杂度,只考虑LoS路径和单次反射路径,忽略了其他的多次反射路径。图2中点画线为近端散射体的单次反射路径,虚线为远端散射体的单次反射路径。根据图2的山地场景3D GBSM模型,基站天线p和移动台天线q之间的信道冲击响应(channel impulse response, CIR)是由LoS分量和近、远端散射体的SB分量叠加而成。CIR表达式为
hpq(t)=hLoS(t)+hSB1(t)+hSB2(t)
(1)
(1)式中,hLoS(t),hSB1(t)和hSB2(t)可分别表示为[16]
(2)
(3)
(4)
(2)—(4)式中:K为莱斯因子;λ为载波波长;fmax为移动台最大多普勒频移;相位θS,θD分别为服从[-π,π)上均匀分布的随机变量。
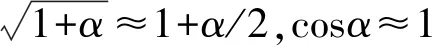
(5)
(6)
(7)
(8)
(9)
(5)—(9)式各参数的表达式见(10)—(11)式。
(10)
(11)

(12)
(12)式中:φ,φ∈[-π,π],φ0,φ0∈[-π,π]分别为φ和φ的均值;k(k≥0)值的大小由散射体分布密度决定,散射体分布密度越大,k值越小[14]。由于近、远端散射体分布密度不同,可用k1,k2值加以区分。

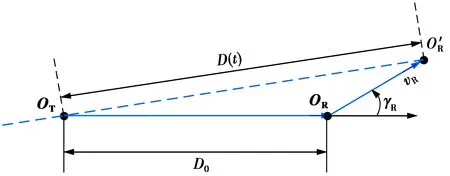
图3 3D信道模型的时变距离参数Fig.3 Time-varying distance parameters of 3D channel model
(13)
莱斯K因子与D(t)之间的关系可表示为[1]

(14)
2 3D GBSM理论模型统计特性
2.1 空时相关函数STCF
任意2个子信道hpq(t)和hp′q′(t)的空时相关函数(space-time correlation function, STCF)可表示为[19]
(15)
(15)式中:E{·}表示数学期望运算;*表示复共轭运算。由于LoS分量和近、远端散射体的SB分量相互独立,(15)式可由不同分量的STCF之和表示为
(16)
LoS的STCF可写为
(17)
近端散射体SB的STCF为
(18)
(18)式中,
(19)
远端散射体SB的STCF为
(20)
(20)式中,
(21)
2.2 空间互相关函数CCF
在 (15) 式,(17) 式,(18) 式和(20) 式中令τ=0,可以得到空间互相关函数(cross correlation function, CCF)的表达式为
(22)
LoS的CCF可写为
(23)
近端散射体SB的CCF为
(24)
远端散射体SB的CCF为
(25)
2.3 时间自相关函数ACF
在(15) 式,(17) 式,(18) 式和(20) 式中令δT,δR=0,于是得到时间自相关函数(auto correlation function, ACF)的表达式
(26)
LoS的ACF可写为
(27)
近端散射体SB的ACF为
(28)
远端散射体SB的ACF为
(29)
3 3D GBSM仿真模型
在3D GBSM理论模型中,考虑有限个散射体的情形,可以得到对应的仿真模型。由 (16) 式,(23)—(25)式可得仿真模型的空间CCF,表示为
(30)
LoS的CCF为
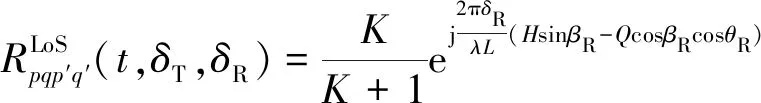
(31)
近端散射体SB的CCF为
(32)
(32)式中,
(33)
远端散射体SB的CCF为
(34)
(34)式中,
(35)
由(16)式,(27)—(29)式可得仿真模型的时间ACF,可写为
(36)
LoS的ACF为
(37)
近端散射体SB的CCF为
(38)
远端散射体SB的CCF为
(39)
4 仿真结果

图4给出了不同的发射天线间隔δT和接收天线间隔δR对应的空间CCF值。CCF是由直射分量、近端散射体反射分量和远端散射体反射分量相加所得,其中直射分量占主导。可以看出,随着δR的增大,空间CCF的绝对值呈减小趋势,而δT对空间CCF值的影响甚微。当δR进一步增大时,反射分量对CCF的影响增加,导致CCF值随δT,δR的变化发生波动。还可看出,当δR值较大时,随着δT的增大,CCF值波动的幅度降低,波动的频次增加。因此,通过调整接收端的天线间隔即可获得较低的空间CCF值。
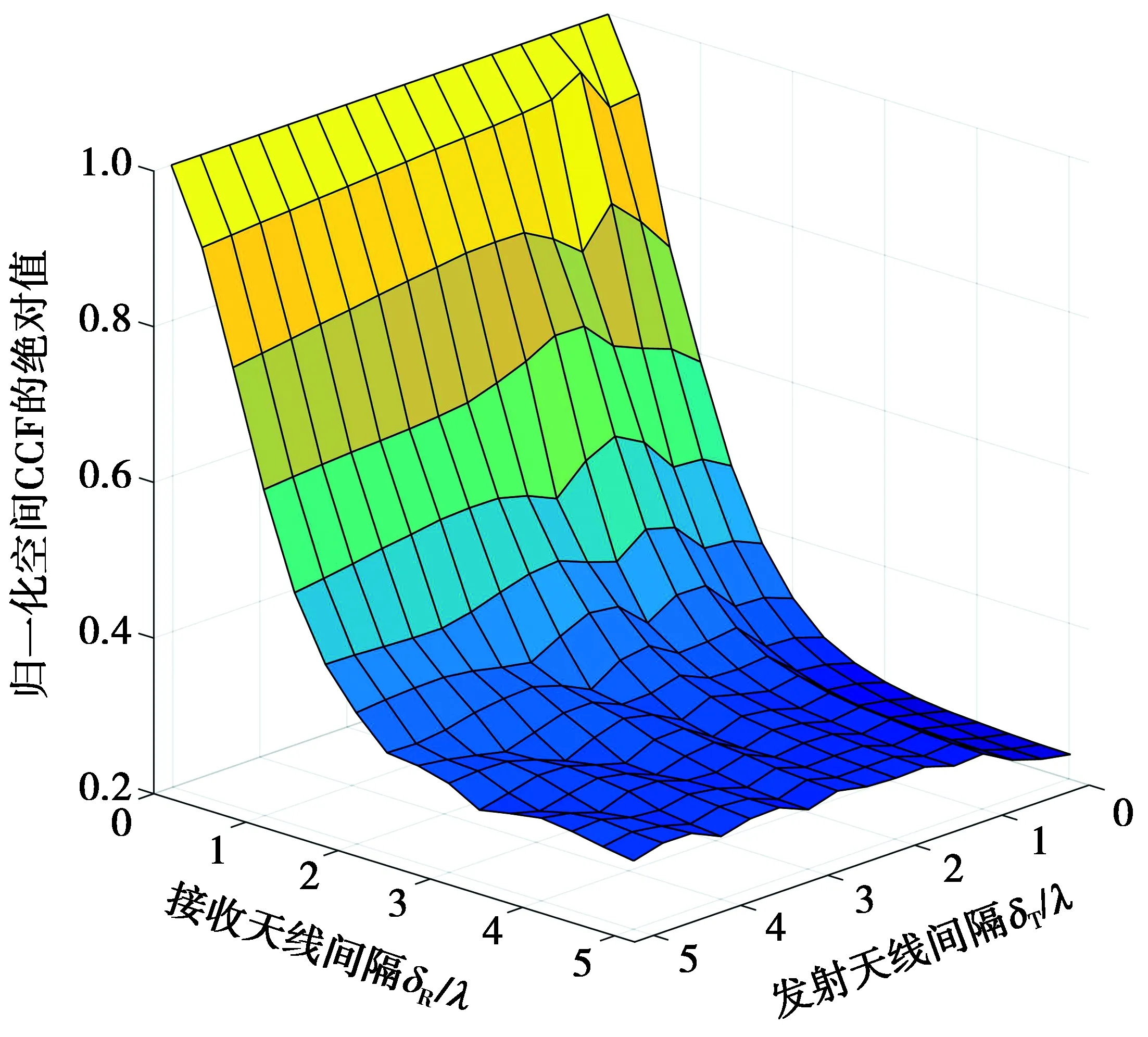
图4 不同天线间隔δT,δR的空间CCF绝对值Fig.4 Spatial CCF for different antenna spacing δT , δR

图5 当δT=λ, t=0 s时,2D及3D GBSM模型的 空间CCF值Fig.5 Spatial CCF for 2D and 3D GBSM model (when δT=λ and t=0 s)
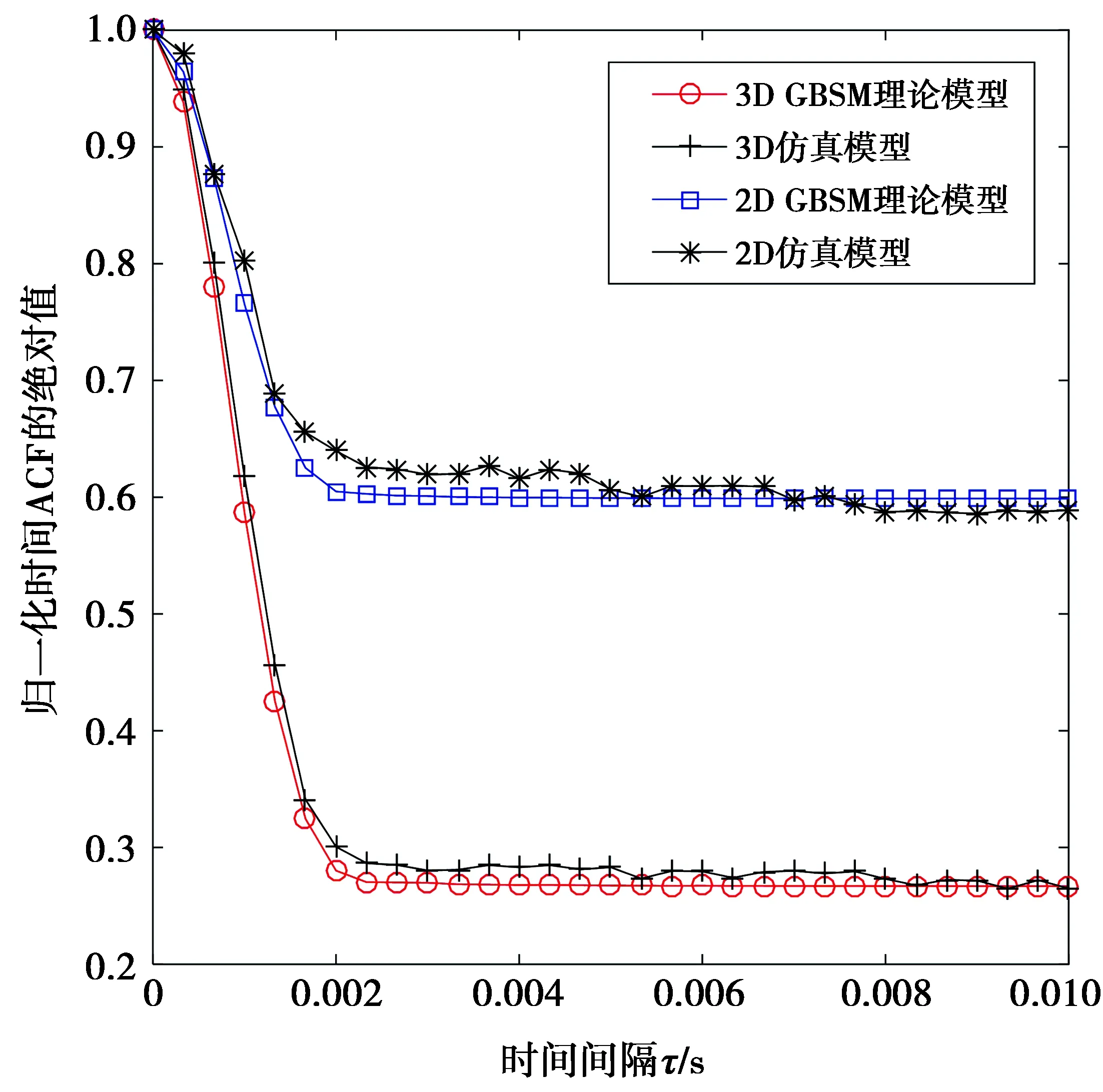
图6 当t=0 s时,2D及3D GBSM模型的 时间ACF值Fig.6 Time ACF for 2D and 3D GBSM model (when t=0 s)
由图5和图6可看出:仿真模型和理论模型得到的空间CCF、时间ACF的曲线贴合度较高,验证了3D GBSM模型公式推导的正确性以及仿真过程的合理性。
由图5可知,当δR较小时(≤2λ)空间CCF受δR的影响显著,但随着δR的进一步增大,空间CCF值的增加趋于缓慢。由图6可知,当时间间隔τ较小时(≤0.002 s)时间ACF受τ的影响显著,但随着τ的进一步增大,时间ACF曲线将趋于平缓。由图5、图6还可看出:3D模型的空间CCF和时间ACF值均小于2D模型的值。这是由于,2D模型无法捕获垂直平面上无线电波的空间多样性,与3D模型相比,它高估了信号的空间相关性、低估了空间分集增益。
图7、图8分别为不同时刻(由移动台的移动引起)的3D GBSM理论模型与仿真模型的空间CCF和时间ACF曲线。由图7、图8可知,不同时刻(t分别取值为0 s和2 s)的空间CCF和时间ACF曲线差异显著。这是因为,不同时刻对应的D(t)值的变化引起了莱斯K因子值的变化,见(14)式。
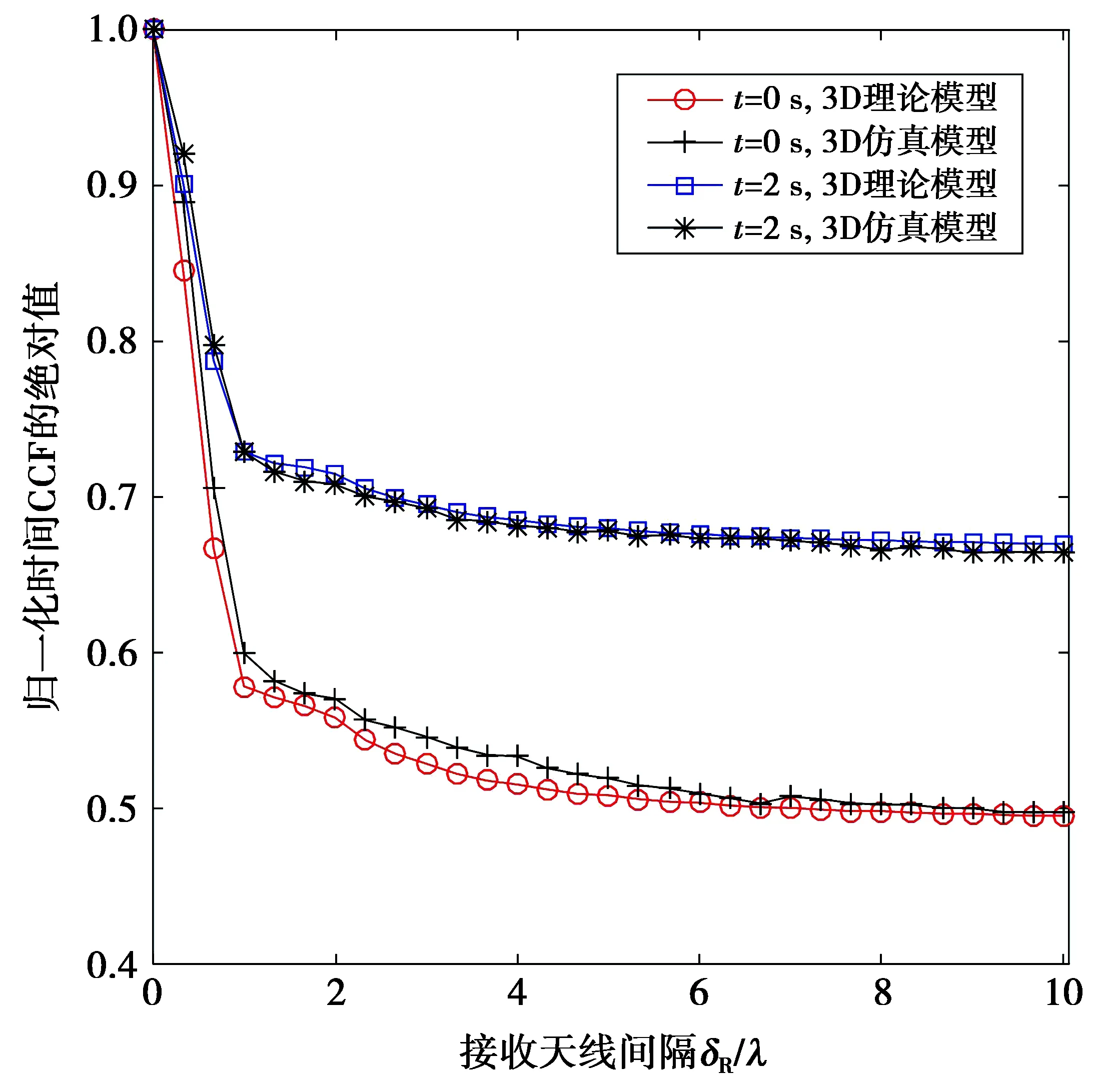
图7 当δT=λ时,不同时刻的3D GBSM模型的 空间CCF值Fig.7 Spatial CCF for 3D GBSM model at different times (when δT=λ)

图8 不同时刻的3D GBSM模型的时间ACF值Fig.8 Time ACF for 3D GBSM model at different times
图9、图10分别为基站和移动台之间的距离D(t)变化对3D GBSM模型的空间CCF和时间ACF的影响。由图9和图10可以看出:移动台无论处于近端区域还是远端区域,空间CCF值和时间ACF值都会随着距离D(t)的增大呈下降趋势,这是由于D(t)的增大引起了莱斯K因子值的减小。

图9 距离D(t)与3D GBSM模型空间CCF值的关系Fig.9 Relationship between distance D(t) and spatial CCF
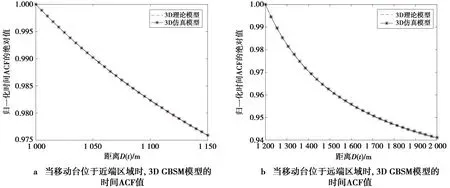
图10 距离D(t)与3D GBSM模型时间ACF的关系Fig.10 Relationship between distance D(t) and time ACF
近、远端散射体分布密度(以参数k1,k2表征)对3D GBSM模型空间CCF性能的影响见图11。由图11可知,随着k1,k2值的增大,空间CCF值呈减小趋势。这说明,散射体分布密度较低的环境(较高的ki值),3D模型的空间CCF值较小。此外,对比图11a和图11b,可看出,远端散射体分布密度k2的变化对空间CCF的性能影响更为显著。
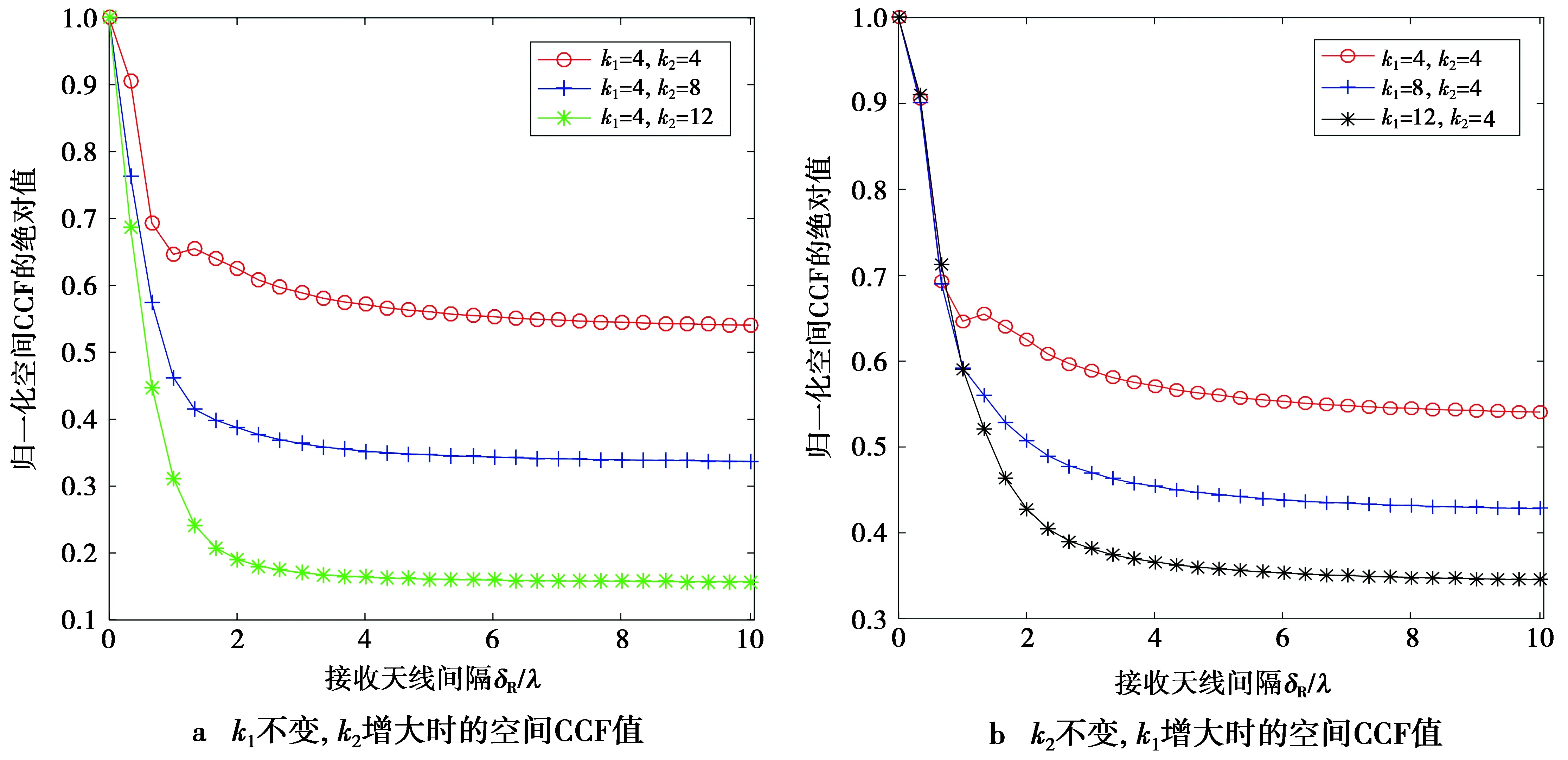
图11 近、远端散射体分布密度与空间CCF值之间的关系Fig.11 Relationship between distribution density of near and remote scatters and spatial CCF value
5 结束语
本文研究了高铁山地场景的3D MIMO无线信道建模问题,推导了信道冲激响应函数CIR以及空时STCF、空间CCF和时间ACF的数学表达式,仿真得到结论:1)相比2D模型,提出的3D GBSM信道模型考虑了散射体相对于基站和移动台的仰角,并对近、远端散射体进行了区分,能够更真实地反映无线电波的空间多样性;2)通过调整收发天线间隔δR,δT,可以获得较低的空间CCF值;3)移动台在运动过程中会引起莱斯K因子值的变化,从而导致空间CCF和时间ACF值发生波动;4)近、远端散射体分布密度较低信道环境下的空间CCF值较小。
未来的研究工作将围绕以下内容展开:模型仿真数据与实际测量数据的对比研究;分析反射路径的数目、山地传播环境的差异性对GBSM 3D信道模型的通用性影响;定性分析多维联合多种参数下的GBSM 3D信道特性,研究信道模型随影响参数的变化规律并提取参数值。

