基于双非凸约束的遥感图像高密度条带去除算法*

孔祥阳,徐保根,李传伟,赵家林

(1.西北工业大学 自动化学院，陕西 西安 710072;2.四川工程职业技术学院 基础教学部，四川 德阳 618000;3.华东交通大学 理学院，江西 南昌 330013)

0 引 言

遥感图像含有丰富的空间和光谱信息，因此被广泛应用于军事、天气预报、农业监测等领域。然而，由于遥感成像系统在采集遥感图像过程中标定误差和不同探测器之间的响应不一致等原因，容易使获得的图像中出现条带噪声(简称条带)。条带的存在不仅会严重降低视觉效果，而且会对后续的应用(如配准，分割和边缘检测等)产生不良影响。因此，去条带是提高遥感图像质量的必不可少的步骤[1～3]。

当前去条带方法大致可分为三类,滤波基方法主要包括小波分析，傅里叶域滤波器和组合滤波器。该类方法在去除周期性条带方面表现出优越的性能。然而，该方法会将具有相同频率的有用信息视为条带而进行滤除，由此造成模糊或振铃效应。统计基方法主要包括矩匹配和直方图匹配及其改进方法。前者假设每个传感器获得的平均值和标准差相同，而后者使用目标信号的直方图去匹配参考经验累积分布函数(ECDF)。因此，该类方法的结果很大程度上取决于预先建立的参考矩或直方图。然而，在实际获取的图像中很难找到合适的参考矩或直方图[4～6]。优化基方法通常将条带和干净图像的先验知识引入能量函数中进行恢复。基于条带的方向特性，即条带只影响沿一个方向的梯度信息，而不会改变沿另一个方向的梯度信息，Bouali M等人[7]首先提出了单向变分模型(UTV)。然而，该方法不能准确识别出条带区域和无条带区域，并且当条带强度比较大时容易产生不良的结果。为了克服该方法的局限，Chang Y等人[8]提出了一种将UTV模型与条带稀疏先验相结合的联合模型，Chen Y等人[9]将组稀疏约束和全变分正则化相结合进行去条带。Dou H X等人[10]提出了一种用于去除条带的定向L0稀疏模型。条带密度的衡量指标有两个[11]，即强度(用I表示)和比例(用R表示)，I和R的值越大表明条带密度越高。虽然这些方法都取得了较好的结果，但是当条带密度较高时，尤其是在非周期条带的实验结果中容易产生块状效应。

本文针对遥感图像中高密度条带去除中条带残留较多或易出现块效应的问题，通过分析条带和干净图像的性质，提出了一种基于双非凸约束的高密度条带去除算法。

1 模型提出

从数学角度可以将条带分为加性条带[7]和乘性条带[12]，而乘性条带可以通过对数变换转化为加性条带[13]，所以一般的文献中均考虑的是加性条带[4]，其退化模型为:F=U+S+N。其中F，U，S，N分别表示观测到的退化图像、待恢复的干净图像、条带噪声和高斯白噪声。该问题是一个病态逆问题，无法直接得到问题的解，因此本文将结合条带和干净图像的先验信息，同时估计出条带和干净图像。

1.1 条带的性质分析

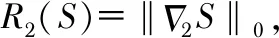
1.2 干净图像的性质分析

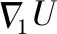
2 模型的优化

去条带模型为

(1)

式中 有两个非凸L0正则项，为了找到近似的方法，首先给出引理1，即均衡约束数学规划(MPEC)[13]，将非凸优化L0正则化项转化为等价的凸优化问题。然后可以利用近端交替最小化(PADMM)算法来求解，同时在理论上保证了收敛性。

引理1(均衡约束数学规划方程[13])对任一给定的向量w∈n,有成立，其中〈〉表示两向量的内积，⊙表示按元素的积，|w|表示对w的每个元素取绝对值，该方程的唯一最优解为v*=1-sing(|w|)，其中当x>0时，sign(x)=1;当x=0时，sign(x)=0;当x<0时，sign(x)=-1。

引入辅助变量P，Q，G可得上式的增广拉格朗日函数为

(2)

式中Λ1为拉格朗日乘子，βi为平衡参数，i=1,2,3,4。

下面对各个变量进行交替更新，并在更新过程中保持其他变量不变。更新G的问题为

(3)

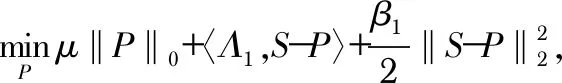
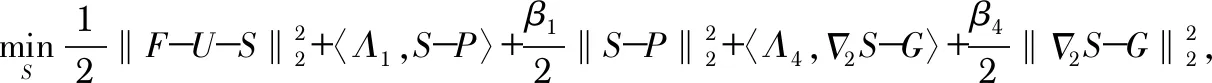
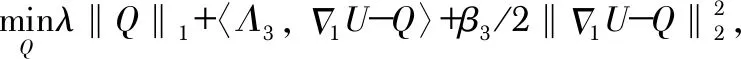
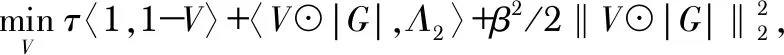
3 实验结果与分析

在合成数据上进行仿真实验，将所提算法与最新的两种方法(DL0)模型[10]和GS[9]进行比较。将从定性分析和定量分析两方面进行比较，定性分析为视觉效果，定量分析包括平均峰值信噪比(MPSNR)[16]和平均结构相似度(MSSIM)[16]。这两个指标的值越大，表明恢复出的图像质量越好。所有的实验基于台式机8 GB内存，3.30 GHz Intel®CoreTMi5—4590处理器，用MATLAB R2016a编程实现，操作系统为Windows7。

3.1 定性分析

在测试图像1中添加密度为I=70，R=0.7的条带后的去噪结果如图1所示。从图中标记的区域可以看出对比的两种算法的结果中出现了原本不属于原图像的暗条带。而本文方法得到的结果与原图更接近。

图1 I=70,R=0.7时周期条带去噪结果

图2为在测试图像2中添加密度为I=100,R=0.9的条带后的去噪结果。不难看出，对于高密度非周期条带，对比的两种方法的结果都产生了较明显的块状效应，而本文的方法则没有。由此可见，本文的方法在高密度条带噪声的情况下仍能够较好地保持图像的边缘和细节信息，去条带效果明显优于对比的两种方法。

图2 I=100,R=0.9时非周期条带去噪结果

3.2 定量分析

表1和表2分别给出了不同噪声水平下模拟周期和非周期条带的定量指标结果。由实验结果可知，本文提出的方法在这些指标上都优于比较的两种方法，并且几乎在所有情况下都有明显的改进。尤其在PSNR值方面，本文方法的PSNR值在周期条带情况下较GS和DL0中的最大值高出约1.5～3 dB，在非周期噪声情况下较GS和DL0中的最大值高出约2.5～10 dB。此外，随着条带密度的增加，比较方法的视觉效果及PSNR和SSIM值出现明显地下降，而本文方法得到了稳定的结果，这表明本文方法较比较方法具有更强的鲁棒性。

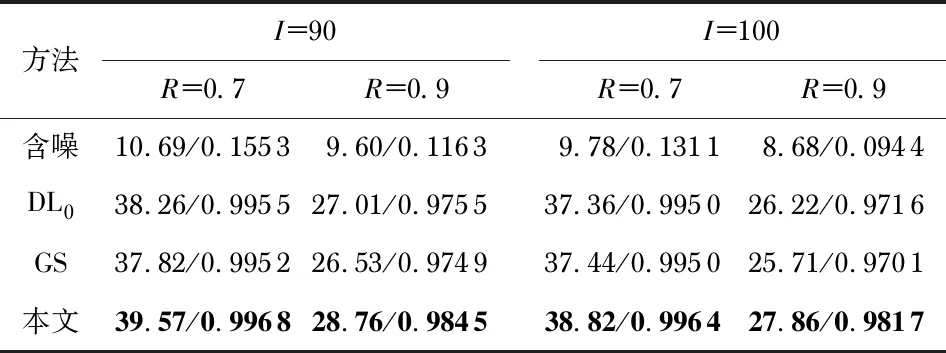
表1 周期条带情况下不同密度条带的PSNR/SSIM值

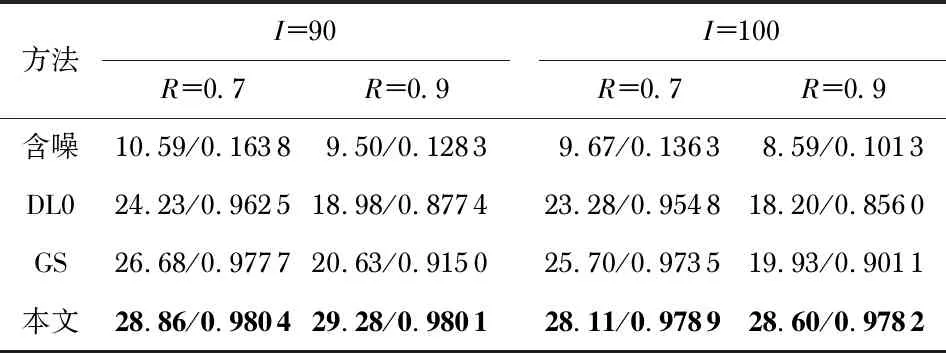
表2 非周期条带情况下不同密度条带的PSNR/SSIM值

4 结 论

本文方法避免了在处理高密度条带时出现的条带残留较多及块效应问题。实验表明，本文算法在视觉效果上能够较好地保持图像的细节和边缘信息，在PSNR和SSIM客观指标上与DL0和GS方法相比有较大的提升。