分组自适应模糊神经网络在双摆吊车上的应用
刘惠康, 孙博文, 柴 琳, 鄢梦伟
(武汉科技大学信息科学与工程学院, 武汉 430000)
作为最常见的重型货运工具,桥式吊车被广泛应用于港口、道路建设、钢厂车间等国民经济建设的各个领域。随着制造业、运输业等工业领域朝着大型化、智慧化高速发展,吊车的高效率、高安全、高精度的需求日益提升。迄今为止,中国多数工业吊车依然是凭借工人经验手动定位与消摆,效果并不理想,会出现定位精度差、操作效率低、消摆效果差等问题[1]。例如:高温熔融金属调运时,微小的摆幅就会带来巨大的危害,实现“零摆幅”吊运刻不容缓。因此,如何保证台车的快速、准确定位,并充分抑制负载的摆动成了中外学者研究的热点。
桥式吊车是典型的欠驱动系统,无法直接对负载进行消摆,在不影响自身定位的情况下,只能通过控制台车运动,从而抑制并消除负载的摆动,中外众多学者为此做了大量的研究工作。吊车的开环控制技术包括输入整形控制、最优控制技术[2];闭环控制技术包括自适应控制[3]、模糊逻辑控制[4]和非线性控制技术[5]等。马博军等[6]利用李雅普诺夫原理和拉塞尔不变性理论证明了好散理论在自适应控制器上的可行性,该控制策略有效解决部分工业吊运过程中负载摆动的问题;华客强[7]将模糊控制推理应用到消摆控制上;陈鹤等[8]基于高斯伪谱法将约束优化问题转化成非线性规划问题,该方法更注重双摆吊车系统吊运效率,通过仿真验证这种方法可以得到具有消摆能力的全局时间最优轨迹。虽然模糊控制对未知数学模型的被控对象有良好的控制效果,但双摆桥式吊车是一个复杂的多变量高阶非线性系统,模糊规则“爆炸”引起的时效性不理想问题亟待解决。神经网络算法具有很强的自适应自学习能力,如果由人为经验输入的样本参数学习与训练不当,训练速度下降甚至陷入局部极小值。
基于上述问题,对双摆型桥式吊车系统欠驱动模型进行建模,利用Lagrange方程[9]得出双摆桥式吊车的状态方程矩阵,并证明其可控性,再将模糊控制拟人决策能力与神经网络学习、自适应的优点相结合,提出一种神经网络模糊控制算法,不仅使台车与负载快速、精确到达目标位置,还有效抑制吊钩及负载摆动,提高了控制器性能。
1 双摆桥式吊车动力学模型的建立
由于工业双摆桥式吊运系统较为复杂,系统除了具有非线性和欠驱动强耦合的特点之外,还会受到不可避免的摩擦力与外界干扰的影响,通过分析桥式双摆吊车系统的特点,对双摆吊车进行动力学模型建立并作出如下假设[10]。
(1)钢丝绳质量相对负载质量可忽略不计。
(2)钢丝绳刚度强,不考虑钢丝绳在吊车摆动过程中发生的长度变化。
(3)吊钩与负载只能于铅垂面内摆动运动。
(4)忽略空气阻力、风阻和高温熔融金属吊运震荡所产生的阻力。
双摆桥式吊车系统吊运的动力学模型如图1所示。

M为台车质量;m1为吊钩质量;m2为负载质量; l1为小车与吊钩间绳长;l2为与吊钩与负载间绳长;α为钩摆角; β为负载摆角;F为对吊车的拉力图1 双摆桥式吊车结构示意图Fig.1 Schematic diagram of double pendulum bridge crane structure
根据双摆桥式吊车,由拉格朗日方程[11]可得
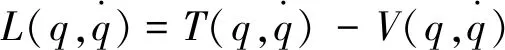
(1)
式(1)中:T为双摆吊运系统的动能;V为双摆吊运系统的势能;q为双摆吊运系统的水平位移坐标;L为拉格朗日算子,表达式为
(2)
式(2)中:fi为系统所受的外力。
系统动能为
(3)
系统势能为
V=m1g[l1(1-cosα)+l2]+m2g[l1(1-cosα)+l2-l2cosβ]
(4)
式中:g为重力加速度;vM、v1、v2为台车、吊钩、负载的速度。根据式(3)、式(4)可得

(5)
式(5)中:b为台车受到的摩擦阻力。
当系统摆角足够小时,对系统进行线性化处理,则

(6)
则模型可以简化为
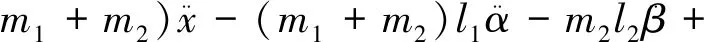

(7)
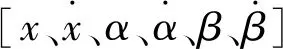

(8)
A=
2 神经网络模糊控制器的设计
神经网络[12]可以自适应调整参数进行学习训练,但内部结构未知,等同于特定的学习和训练过程在黑箱中进行,无法了解其内部运行情况。对于非线性系统参数优化问题,神经网络权值[13]根据局部改善的方向调整,极易陷入局部最优化。模糊控制基于模糊推理与模糊语言可以表达不确定信息,并根据实际控制情况结合主观控制经验制定模糊规则,但没有在线自学习能力,不能反映实时状态且不具备自适应优化参数的能力。复杂的非线性系统模糊控制,由于控制系统输入增多,模糊规则呈指数增长将会十分复杂,影响整体系统运行的时效性,运行效率不佳。神经网络模糊控制算法把模糊化和模糊推理结合神经网络中的神经元,显著提高神经网络运行可读性与灵活度,不断训练优化隶属度函数,综合了各自的优势。该控制策略不仅融合模糊控制的拟人决策能力,还具备神经网络的自适应自学习与并行泛化处理能力,将更好地解决双摆吊车高温熔融金属吊运中的定位与消摆问题。
神经网络模糊控制算法普遍使用的有三类:第一类是在神经网络算法之中运用模糊运算,普通神经元及其模糊神经元同时在神经网络中处理模糊信息,一般运用随机搜索法或反向传播算法不断进行学习与修正;第二类神经网络模糊控制算法主要重点为模糊逻辑优化,利用先进的模糊逻辑优化神经网络算法,得到启发式知识进行寻优,收敛时效性提高;第三类神经网络模糊控制是基于神经网络的模糊系统,利用神经网络对模糊逻辑分层优化,提高系统的灵活度。
2.1 引入Takagi-Sugeno模糊模型的神经网络
模糊推理有Mamdani型和Takagi-Sugeno型,不同模糊推理特点优势不尽相同。Mamdani型模糊推理规则形特点是注重拟人化思维和语言表达习惯,更善于表达人类知识策略,有着十分复杂的计算结构,数学分析要求较高相对困难。Takagi-Sugeno型模糊推理的优势是规则简单,与自适应方法的匹配度较高,所以可以融合拟人推理思想的模糊理论与自适应、自学习能力的神经网络结合的先进控制策略,并且MATLAB还提供了合适的函数用于仿真。
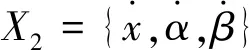
如图2所示,神经网络模糊控制器的多输入复杂结构通过分组权重系数优化转变为一阶误差E与二阶误差EC的两输入且单输出神经网络模糊控制结构。

图2 神经网络模糊控制权重分组结构图Fig.2 Weight grouping structure chart of neural network fuzzy control
其中,综合误差E与综合误差EC变化率为
(9)
用矩阵形式表达模糊控制分组结构中的权重综合系数K为
K=[k1k2k3k4k5k6]
(10)
利用单点模糊集合的模糊化方式融合多组的输入数据,根据每条规则的适应度调节加权权值,再结合双摆桥式吊车建模的系统状态方程,利用二次型最优控制控制方法理论,设计优化加权矩阵Q和R的值,可以得到多组初始数据为训练数据做准备。对于一阶误差E与二阶误差EC的两输入且单输出神经网络模糊控制规则,可表示为
(11)
式(11)中:Ai与Bi为模糊集合;pi与qi为模糊规则参数;ri为补充参数。模糊神经网络的输入变量用高斯隶属度函数gxi(x,ai,bi)和gyi(y,ci,ci)表示,其中i=1,2,模糊神经网络的输出变量为各输出量的加权平均线性化表示,系统结构如图3所示。
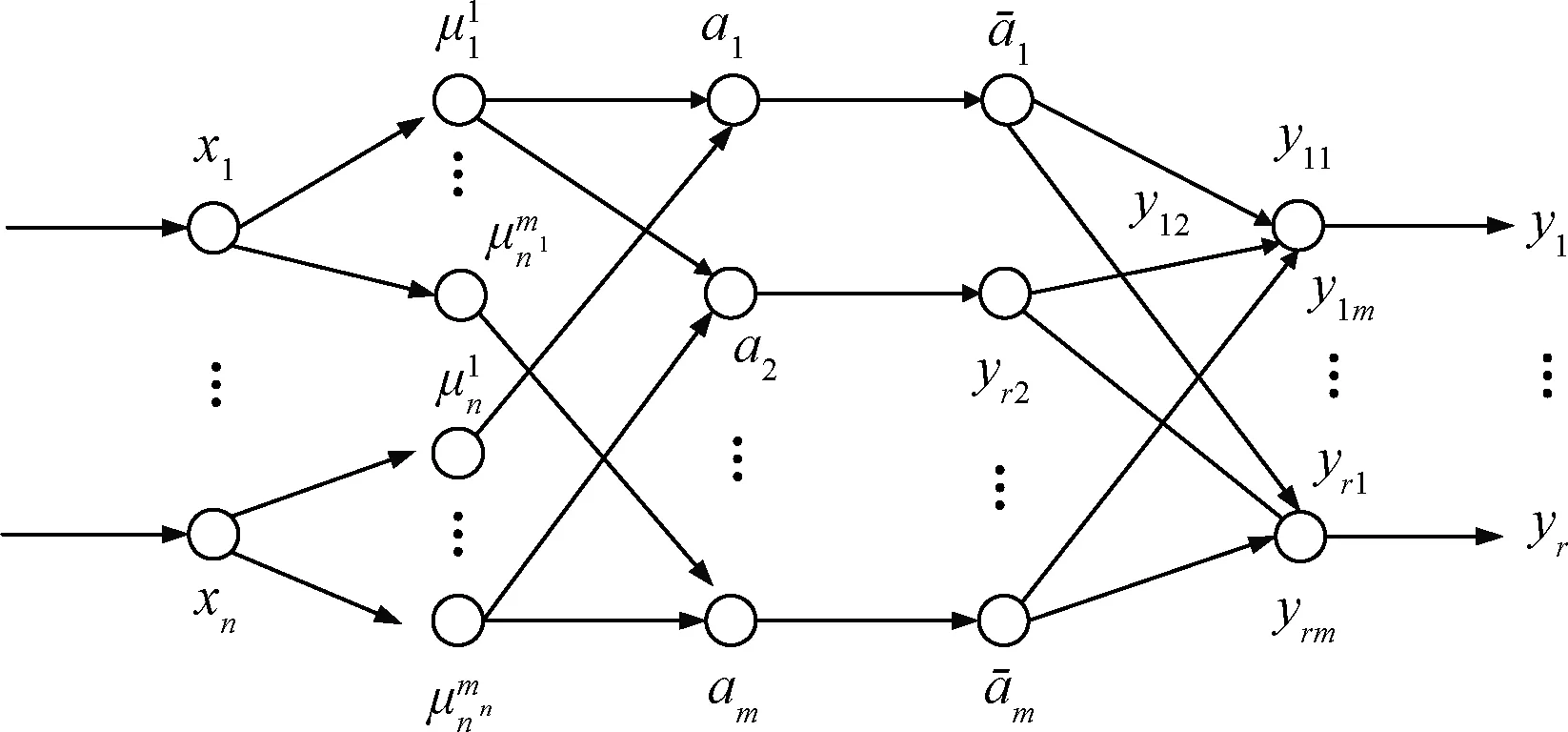
图3 基于Takagi-Sugeno模型的模糊神经网络系统结构Fig.3 Fuzzy neural network system structure based on Takagi Sugeno model
第一层:本层对系统输入模糊控制范围内的隶属度函数分析计算,导入分组融合数据,一阶误差E和二阶EC成为输入量接收到神经网络系统中,将输入量x=[x1,x2,…,xn]T传送给下一层。
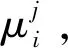
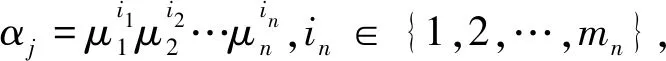
第四层:神经网络模糊控制模型中,模糊逻辑推理的运算完成过程主要分布在第三层与第四层,其中第三层完成对模糊规则前件的处理,第四层负责运算推理模糊规则后件。逻辑推理后的后件输出模糊量,可以进行归一化计算,即
(12)
第五层:本层主要是通过解模糊将模糊推理逐步量化清晰化的输出,即
(13)
式(13)中:wij为权值系数。
2.2 神经网络模糊控制参数优化与学习
神经网络模糊控制系统利用分组融合的策略,降低系统输入的数量,引用高斯隶属度函数将一阶误差E与二阶误差EC模糊化。在Takagi-Sugeno模糊推理系统中,利用隶属度函数将模糊变量逐步清晰量化为实际台车牵引力。神经网络模糊控制策略可以不依赖于传统人工经验自适应调整输入输出值。神经网络模型通过调整隶属度函数的中心、宽度、斜率等对前提参数和结论参数利用梯度下降法[14]与最小二乘法结合进行自学习与优化,提升了系统运行与辨识速度。前提参数优化时,梯度下降法利用学习训练中的反向学习,控制变量锁定输出层参数,准确校正前提参数。结论参数优化时,最小二乘法利用学习训练中的前向学习,控制变量锁定前提参数,准确校对结论参数。反向学习按照微缩误差的趋势逐步对输入及其中间层参数进行优化适应,系统反馈的二阶误差再次优化前提参数,从而做到调整模糊控制中的隶属度函数与模糊规则,这种混合算法可以并行修正,快速收敛,解决传统模糊控制的时效性问题。在混合算法对参数优化过程中,不断迭代修改反馈,对前提、结论参数进行微调训练校正,最终整个样本训练集合的数据达到高精度逼近系统的标准,满足双摆桥式吊车高温熔融金属吊运的定位与防摆要求。
2.3 神经网络模糊系统控制器的设计
通过MATLAB软件[15]对神经网络模糊控制系统进行仿真设计。利用二次型最优控制控制理论,设计优化加权矩阵Q和R的值,可以得到多组初始数据作为样本训练数据。设定合适的隶属度函数,输入数据加载到模糊神经网络控制器中生成FIS(fuzzy inference system)参数。利用样本训练数据对整体参数不断迭代学习训练,最后引入校对数据对所神经网络模糊控制器的FIS性能进行验证。
(1)构建FLS (fuzzy logic structure)模型利用MATLAB中的fuzzy控制工具箱建立一个新的Takagi-Sugeno模型,由于双摆桥式吊车的输入变量合成为一阶误差E与二阶误差EC,用高斯隶属度函数,调节函数的论域为[-3,3],输出变量论域为[-10,10]模糊语言变量值{NB,NM,NS,ZE,PS,PM,PB},其模糊规则为
(14)
(2)获取初始训练与测试数据二次型最优控制控制理论设计计算的数据作为初始样本数据,输入初始样本集合x1,x2,…,xn,可以得出最优台车牵引控制力状态点集合为y1,y2,…,yn。
(3)神经网络模糊控制器完成利用初始样本数据,在MATLAB中调用函数ANFIS,完成神经网络模糊控制器的设定,优化模糊规则和生成新的隶属度函数。最后对输入输出的最优状态点集进行迭代学习优化。
3 仿真实验及分析
为进一步验证神经网络模糊控制方法的有效性,对双摆桥式吊车模型进行建模并建立Simulink模型,根据仿真实验的调试设置了MATLAB/Simulink仿真参数,其中吊车系统参数:m1=1 kg,m2=5 kg,l1=2 m,l2=2 m,g=9.8 m/s2,x=3 m。将上述参数代入双摆桥式吊车系统状态方程[式(7)]并进行仿真,选取Simulink仿真周期T=15 s,并从0时刻开始输入指令xd=3 m,选用神经网络模糊控制器、LQR(linear quadratic regulator)控制器、模糊PID(proportion integration differentiation)控制器进行仿真效果对比。
如图4三种控制器吊车位移控制效果对比图所示,三种控制器均可实现台车快速精准定位,神经网络模糊控制系统在双摆桥式吊车从收到吊运指令后到达系统目标位置并维持稳定耗时为5.5 s,响应速度较快,台车并无残余摆动超调量为零;而同样到达指定位置,模糊PID控制系统由于模糊规则复杂的问题,响应时间过长影响整体吊运效率;LQR控制器虽然响应速度略快,但台车定位准确性欠佳,具有较大超调量,且加权矩阵结构复杂不稳定不利于双摆吊车高温熔融金属吊运。引入分组神经网络模糊控制策略的设计方法,避免了模糊规则爆炸的问题,在吊运效率上有所提升,对台车位移控制效果也要优于模糊PID与LQR控制器。

图4 三种控制器吊车位移控制效果对比Fig.4 Comparison of crane displacement control effects of three controllers
如图5所示,在使用神经网络模糊控制策略时,摆角1偏离平衡位置最大角度为1.93°,在4.3 s后达到稳定状态。摆角2偏离平衡位置最大角度为2.72°,在4.6 s后达到稳定状态。本方法在双摆抗摆上相对于模糊PID控制与LQR控制有较为明显的优势,吊钩与负载的摆动范围最小,有效地提升了双摆桥式吊车系统的暂态控制性能。

图5 三种控制器的摆角控制效果对比Fig.5 Comparison of swing angle control effect of three controllers
如表1所示,双摆吊运系统在神经网络模糊控制策略下各方面效果明显要优于模糊PID控制和LQR控制,尽管模糊PID控制能保证系统无超调量的到达目标位置,但是双摆系统模糊规则冗杂,系统响应时效性欠佳,且双摆最大摆角相对神经网络模糊控制摆幅更大,影响整个吊运系统的暂态控制性能;LQR控制器虽能较好地保证台车运动的时间最优性,且相对模糊PID控制器摆角较小,但是台车定位准确性欠佳易发生超调。LQR控制器利用最优控制理论对加权矩阵中的加权系数进行人工计算调试,易出现较大的误差,不利于高温熔融金属桥式双摆吊车吊运的稳定。综上所述,使用神经网络模糊控制器的双摆吊运系统控制效果最好,台车能够快速响应并准确到达指定位置,提高了整体吊运效率,对于双摆摆动幅度有明显抑制效果,且摆角调节时间更短残余摆动范围更小,消摆效果明显,具备较好的暂态控制性能。

表1 控制器控制效果对比Table 1 Comparison of controller control effect
4 结论
高温熔融金属吊运的定位防摆在冶金行业中具有非常重要的意义,由于中国大多依据工人经验手动消摆,精度差稳定性低。针对这种情况,根据Lagrange方程对双摆型桥式吊车建立二维数学模型,将模糊控制拟人决策能力与神经网络学习、自适应能力相结合,提出一种神经网络模糊控制策略,利用FIS模型对模糊控制器的隶属度函数和模糊规则不断训练优化,提高控制系统暂态控制性能。从仿真结果上看,采用神经网络模糊控制策略的方法不仅使双摆桥式吊车台车与负载快速、精确到达目标位置,还有效抑制吊钩及负载摆动,提高了控制器性能。

