刚柔耦合在仿猫腿跳跃机器人中的功率放大作用

陈贵亮， 黄荣新， 杨 冬

(河北工业大学机械工程学院， 天津 300130)

高效跳跃是运动机器人有待发展的一种能力，在未来，机器人将广泛应用于抢险救灾、军事任务、危险环境作业和星际探索等复杂地形条件下的地面运动任务，需要具有灵活高效的机动能力。

跳跃能力是机器人机动性能好坏的重要标志。但目前已有的机器人中，具有良好跳跃能力的不多。而自然界的许多陆生哺乳动物具有良好的跳跃能力。因此，各种善跳动物的跳跃机理得到广泛研究，并应用于仿生机器人中[1]。孙泽军等[2]对蟋蟀的跳跃机构进行了分析，并研究了仿蟋蟀机器人。王永健等[3]基于松鼠优秀的跳跃性能，分析其起跳过程中腿部的生理结构和运动机理，仿生设计出一种柔性跳跃机构，根据其动力学，研究了其运动规律。郁万春[4]通过对蝗虫的身体结构及跳跃机理的分析，设计了仿蝗虫的跳跃机器人；王猛[5]设计了仿青蛙的跳跃机器人。莫小娟等[6]对比各种现有仿昆虫机器人的跳跃性能，分析了其在实现可控起跳、空中姿态调节和落地缓冲复位等方面采取的策略。宋亚杰等[7]模仿袋鼠腿部机构设计了一种四连杆跳跃机器人，通过凸轮、四连杆和弹簧机构，实现能量的储存和瞬放。国外在这方面的研究也很多，这里不再枚举。

跳跃的实现需要短时间内释放大量的能量，即需要极大的瞬时功率。然而Peter Aerts在对夜猴的跳跃能力及其腿部肌肉的代谢能力的对比中发现，其腿部肌肉所能提供的最大功率远不足以支持跳跃所需，发现了夜猴等哺乳动物通过功率放大实现跳跃的现象[8]。揭示出独特的骨骼构型和肌肉-肌腱的柔性驱动所形成的腿部结构是实现这种功率放大的原因。动物以较小功率的驱动实现高效跳跃的省能机理值得研究、效仿。Plecnik等[9]依夜猴的跳跃机构原理设计了跳跃机器人Salto，可达到11.5倍的功率放大比。

动物机构由骨骼、肌肉、肌腱、腱膜等组成，先天的刚柔耦合构型是其跳跃中省能和功率放大的基础。为了在机器人上应用这种原理，上述研究举例中无一例外地利用了弹性元件，通过能量积蓄、瞬放以实现跳跃的原理。但目前研究主要是对动物机构的直接模仿。其中的刚柔耦合机理需进一步揭示，以使跳跃仿生研究可由机构模仿发展为对原理的自主应用。

猫作为一种常见的善跳动物，在复杂地形具有相当高的敏捷性与灵活性，是良好的跳跃仿生研究模本。猫跳跃中充分利用到前肢、腰部和后肢的协调能力。在对猫跳跃研究中，已经对其腰部运动对跳跃的调节作用进行了分析[10-11]。

后肢是猫产生跳跃的主要驱动机构，对其中弹性蓄能原件通过刚柔耦合作用，在跳跃中形成功率放大的能力的研究，对仿猫跳跃机构的设计很有意义。由于在研究中难以对动物内部机构精确测量、分析，以及受到动物保护法律上的限制，利用模型模仿动物机构的某些特征进行研究是机构仿生研究的重要手段。根据所设计的一个仿猫后肢跳跃机构，对其不同部位的弹性蓄能原件对跳跃效果的影响进行仿真分析，并从跳跃功率的角度对其产生进行揭示。目的是揭示其实现高效跳跃过程中的能量调度现象和能量利用规律。

1 仿猫腿跳跃机构

1.1仿猫腿机构设计

图1(a)所示为猫的后肢骨骼构型，图1(b)所示为根据猫的骨骼构型和肌肉驱动原理简化的猫腿机构。据此设计了图2的仿猫腿机构方案。机构简化为由旋转铰链连接的股杆、胫杆和足杆三部分。AD、EF杆分别代表猫后肢的大腿部分和小腿部分的双关节肌肉-肌腱连接，在此为简化机构，设计为刚性杆，只体现了其对杆件的耦合作用，而未体现其柔性和驱动作用。大腿部分和小腿部分形成相互耦合的两个四杆机构。蓄能弹簧设置于膝关节C和髋关节B点。此机构只具有一个自由度，故只需在髋关节设置驱动即可控制其运动。跳跃过程为由髋关节的驱动电机逆时针扭转股杆，两个四边形变形，使腿形成图2(a)的蹲下状态，此时各弹簧蓄足势能。电机驱动释放，机构在弹簧驱动下展开，向图2(b)状态变形，弹簧中的能量得以瞬间释放，驱动机构跃起。

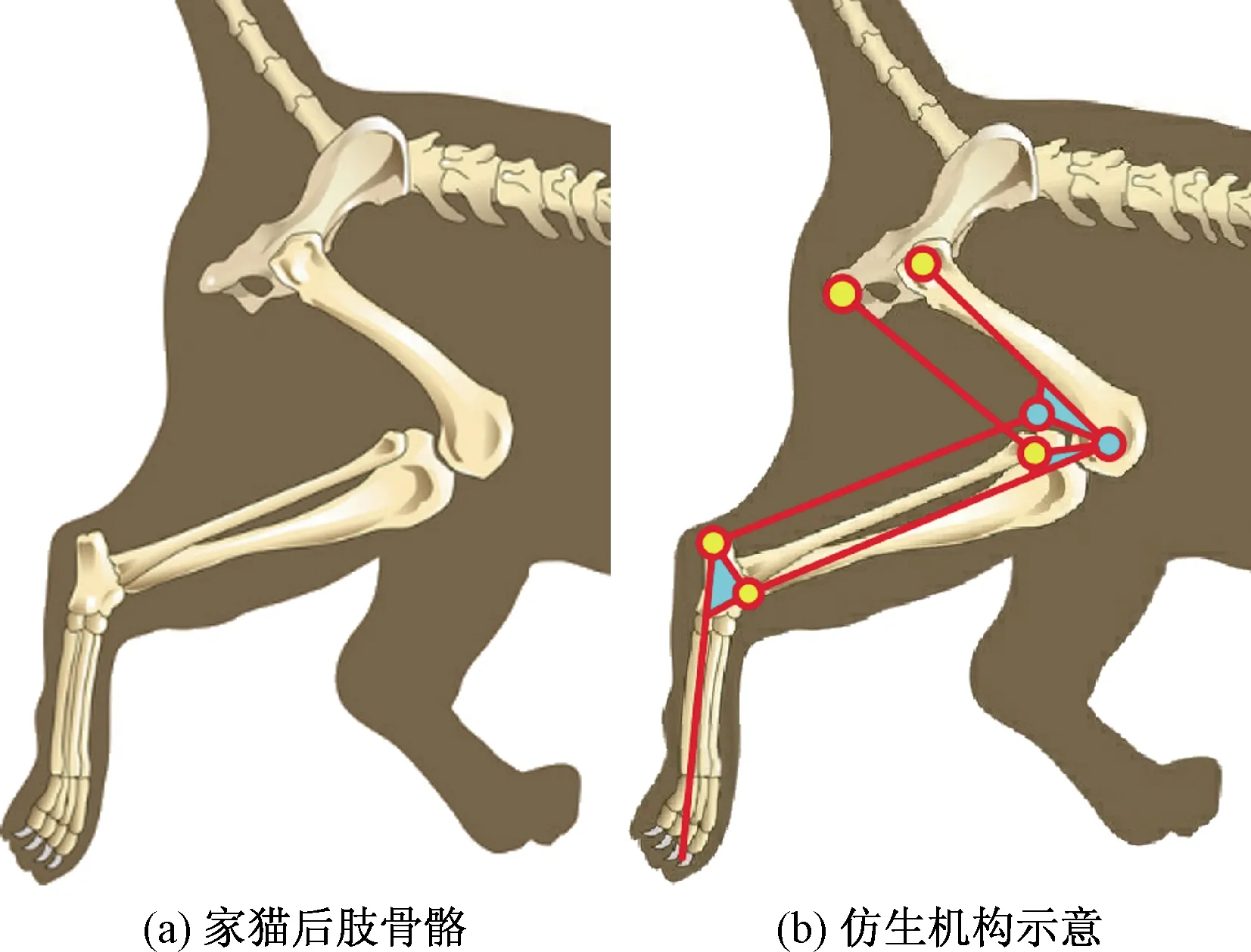
图1 猫的后肢骨骼和仿生骨骼机构Fig.1 The hind limb skeleton of a cat and the bionic skeletal mechanism

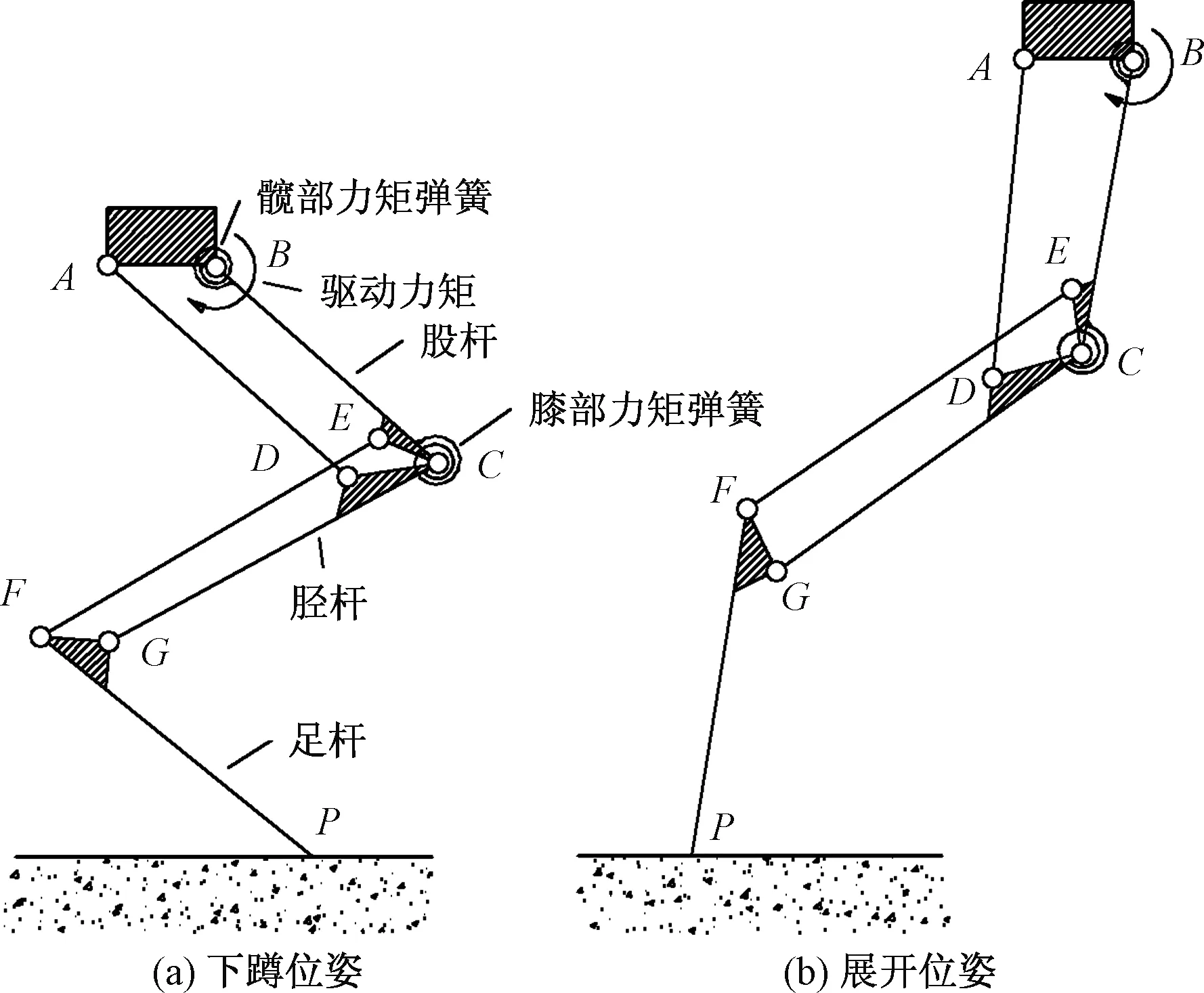
图2 仿生单腿机构简图Fig.2 Schematic diagram of bionic single leg mechanism

机构的各杆长根据对实猫的测量尺寸确定，如表1所示。跳跃中各关节的旋转角度范围根据对猫进行的跳跃实验中高速相机拍摄的腿部机构实际运动范围确定，如表2所示。

表1 仿生单腿机构各杆长度Table 1 The length of each rod of the bionic one-legged mechanism

表2 腿机构最大伸展和收缩位姿各关节角度Table 2 The angle of each joint at maximum extension and contraction position of the leg mechanism

1.2 仿猫腿机构运动学分析

猫的跳跃过程分为着地阶段和腾空阶段，其中着地起跳阶段为腿部肌肉肌腱能量存储与释放的阶段。因此，只对仿生腿机构的着地起跳阶段进行运动学分析。建立如图3所示的腿连杆机构的坐标系和广义坐标参数。其中粗体点划线是理想连杆。假设此节段，足端P与地面接触点无滑动，则足杆PG始终绕P点转动，以其与地面上的对应接触点P0为原点，建立惯性参考坐标系P0-xyz，根据各连杆的结构建立各个连杆坐标系。

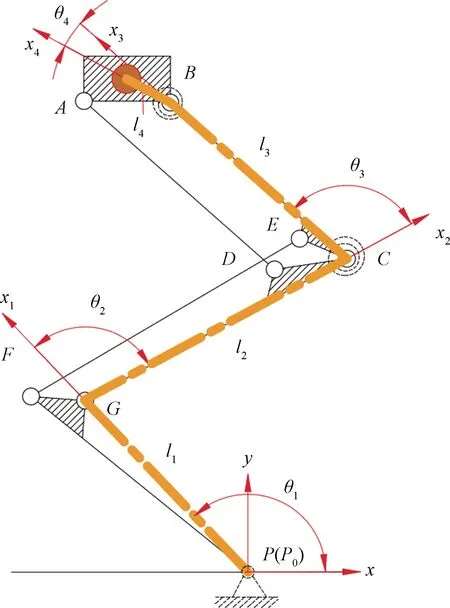
图3 机构坐标系和广义坐标参数Fig.3 The coordinate system of mechanism and generalized coordinate parameters

各杆长度设为li，各杆质心位置为Mi(i=0，1，2，3，4)，其中l4是负载块质心到铰点B的距离。各杆之间相对转角为θi，角度的正负以在前一杆的基础上逆时针旋转方向为正向。副连杆AD、EC选取较轻、细的材料，忽略其质量，分析中即只需考虑4个主杆的质量作用。设第i杆的质心位置距其内侧铰点的距离与该杆长的比例为ρi。另设P点到P0点为杆0，显然l0、M0和θ0均为0。取各关节转角θi为系统广义坐标，各关节坐标和各杆质心位置都是广义坐标θi的函数，各连杆的质心坐标可表示为

(1)

将式(1)分别对时间求一阶导数和二阶导数，得到各连杆质心的速度和加速度，即

(2)

(3)

(4)

(5)

式中：k为z方向的单位向量。

1.3 跳跃功率的计算

由仿生腿机构跳跃时的总质心速度与地面对机构的接触反力可以计算机构的输出功率Po，输入功率Pi可由驱动电机对BC杆的输入力矩Ti和BC杆的角速度计算得到，记为Pi。输出、输入功率和设置功率放大因子C的计算公式为

Po=Ftvt

(6)

Pi=TiωBC

(7)

C=Po/Pi

(8)

式中：Ft为仿生腿机构对地接触力矢量；vt为仿生腿机构总质心跳跃速度矢量。总质心坐标位置和总质心的速度矢量计算公式为

(9)

(10)

式中：i,j为x、y方向的单位向量。

2 仿猫腿机构跳跃仿真

2.1 仿真建模和设置

根据图2结构方案及表1的机构参数，在SolidWorks中建立仿猫腿机构的三维模型，将其导入ADAMS软件，如图4所示。根据方案建立各连杆之间的转动副。机构的驱动力矩电机设置在B铰点，驱动力矩施加于连杆AB和BC之间。

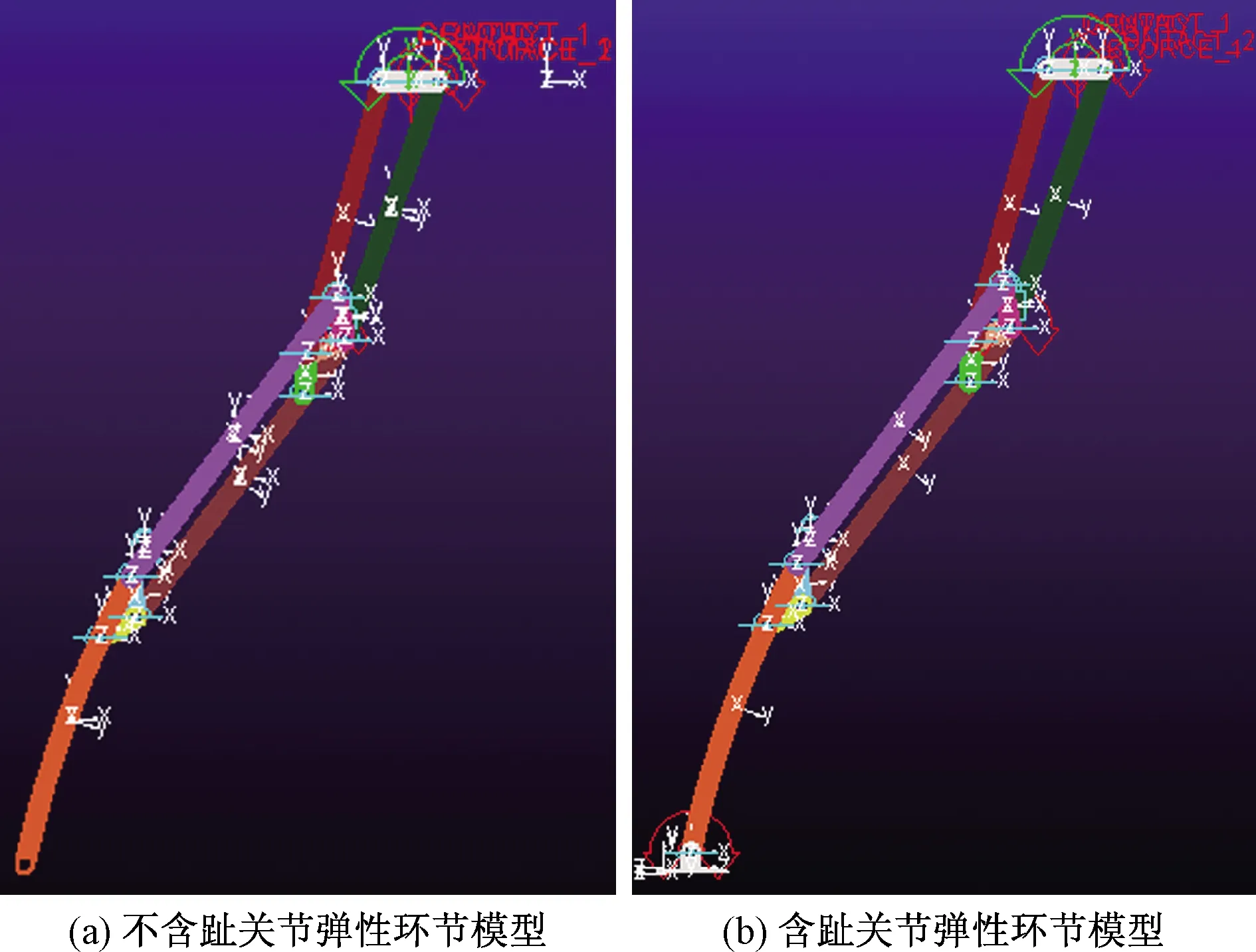
图4 ADAMS中的机构模型设置Fig.4 Setting of mechanism model in ADAMS

以水平方向为x轴，竖直方向为y轴，z轴垂直向外。由于此处是为了检验机构的跳跃驱动能力，为防止机构在各方向上由于不平衡造成的翻转，将机构运动限制在xy平面内，并且限制髋部的AB杆绕z轴转动自由度。

为对比弹性环节在机构中不同布置方案对机构跳跃效果的影响，设置了四个方案对照组：DKT、DK、DT和D。其中，D表示在髋的B点铰链有弹簧；K表示在膝关节的C点铰链有弹簧；T表示在足部的趾端P点附件为弹性材料。如DKT指此组机构在髋关节B铰链、膝关节K铰链和趾关节P铰链设有弹性元件，其余方案以此类推。设置仿生单腿机构的髋部驱动蓄能弹簧刚度为0.3 N·m/(°)，阻尼为5×10-4N·m·s/(°)；膝关节蓄能弹簧刚度为0.2 N·m/(°)，阻尼为5×10-4N·m·s/(°)；趾关节蓄能弹簧刚度为1×10-4N·m/(°)，阻尼为1×10-6N·m·s/(°)；驱动力矩为48.4 N·m。

2.2 跳跃仿真实验

2.2.1 不同关节弹性环节添加或去除对仿生腿跳跃效果的影响

仿真中腿机构运动过程为电机驱动机构收缩至起跳蹲伏姿态，然后释放，机构在弹性恢复力作用下展开，实现跃起。

图5所示为四个对照组的跳跃高度及距离曲线，其中DKT与DK的跳跃高度、距离相近，DT和D的跳跃高度、距离相近，DKT与DK的跳跃高度和距离均接近DT和D的跳跃高度和距离的2倍。说明趾关节的弹性元件对于跳跃能力影响不大，膝关节的弹性元件对于跳跃能力影响较显著。其中起跳时间不同是由于DT和D系统刚性较大，为平稳起跳选择较慢的腿机构收缩速度(收缩是蓄力过程，速度不影响起跳效果)。

图5 仿生单腿机构跳跃对比图Fig.5 Comparison diagram of jump of bionic single-leg mechanism

图6所示为对照组跳跃速度曲线，其中DKT与DK的跳跃速度相近，DT和D的跳跃速度相近。说明膝关节弹性环节对提高起跳离地速度有着显著效果。

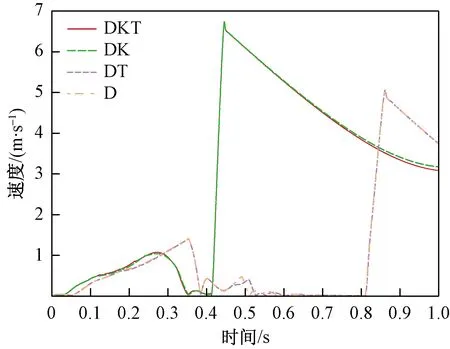
图6 仿生单腿机构起跳速度对比图Fig.6 Comparison diagram of jump velocity of bionic single-leg mechanism

图7所示为对照组对地接触力曲线，其中0.4 s和0.8 s附近的峰值分别为DKT、DK和DT、D组起跳时足部受到的地面接触力峰值，1.7 s和1.8 s附近分别为降落时DKT、DK和DT、D组的足部受到的地面接触力峰值。由图7可见，起跳时对地接触峰值力为DKT和DK较高，且二者比较接近；DT和D较小且数值相近。

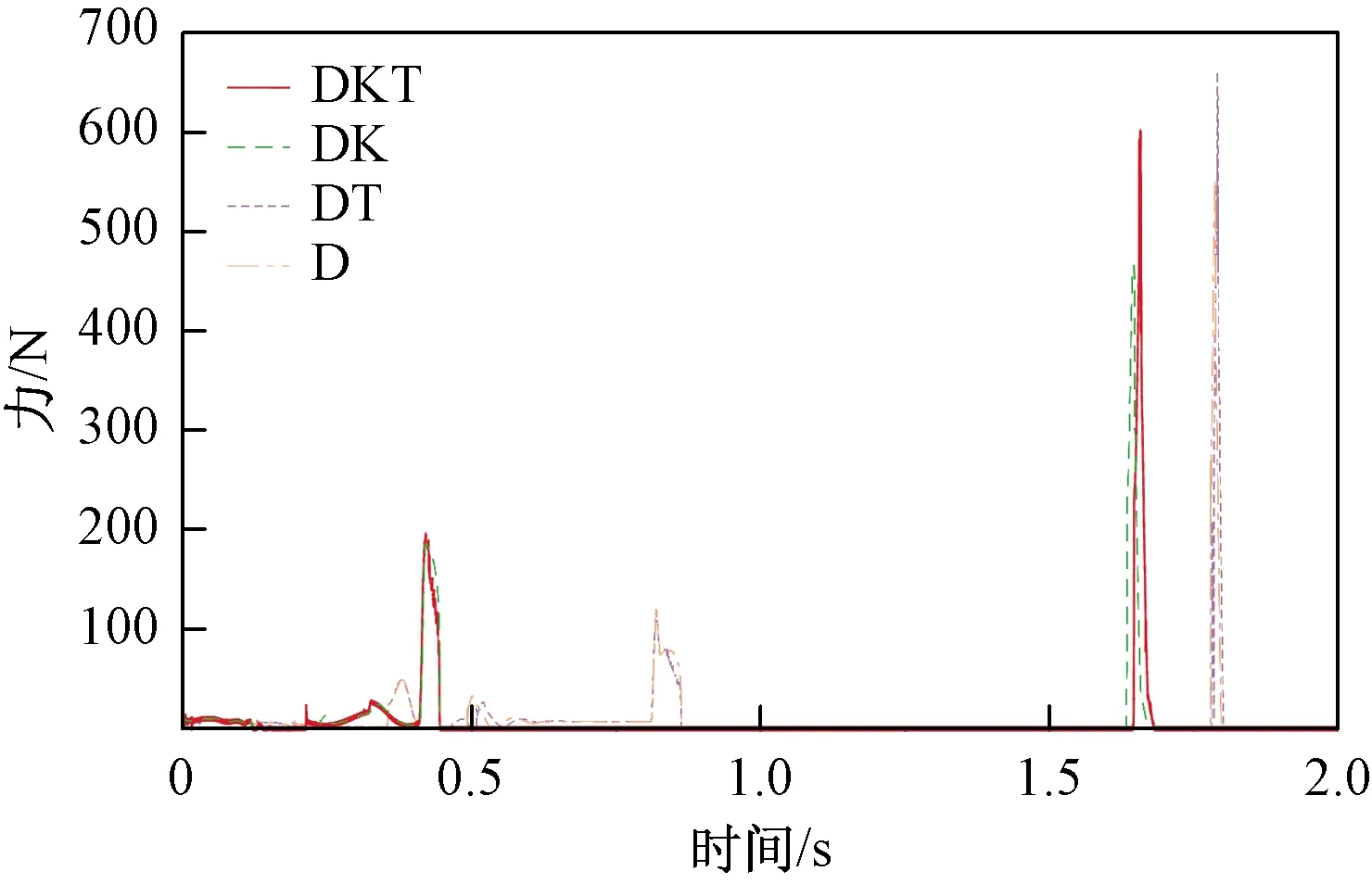
图7 仿生单腿机构对地作用力对比图Fig.7 Comparison diagram of the force to ground of bionic single-leg mechanism

从图5～图7可以看出，DKT与DK的起跳时接触力曲线较DT和D更为平稳，同时也具有较大的起跳时对地压力，从而获得更大的起跳加速度。而在着陆时，对地接触峰值力为DT组最大，D次之，DKT再次之，DK最小。

以上仿真结果所没有表示的是，在该机构中，D、K至少需要具有其一，否则机构很难跳起来。在此以具有D配置为基础条件，比较K和T配置对跳跃效果的作用差异。

由以上可见，在此机构中，膝关节的弹性蓄能原件对跳跃效果的提高贡献较大，在起跳阶段可以获得较大的地面接触反力，提高起跳加速度，获得较大的峰值速度，因而在跳跃高度和距离上均较其他对照组有较大的提高。在降落阶段，该配置可以减小降落冲击力，有益于系统的安全。而趾关节配置的弹性元件对起跳的作用不明显。

2.2.2 膝关节和趾关节弹性环节刚度和阻尼的增大或减小对仿生腿跳跃效果的影响

从图8可知，保持输入力矩大小及作用时长不变，其他参数不变，膝关节弹性环节刚度增大50%时，跳跃高度减少了18.3%，跳跃距离减少了19.1%，起跳时对地作用时长减少了23.2%，对地峰值力增加了18%，落地冲击有效峰值力降低38.8%。刚度减小50%时，跳跃高度减少了15%，跳跃距离减少了16.6%，起跳时对地作用时长增加了18.1%，对地峰值力减少了26.4%，落地冲击有效峰值力升高36.4%。膝关节弹性环节阻尼放大100倍时，跳跃高度减少了39.6%，跳跃距离减少了38.8%，起跳时对地作用时长与初始阻尼条件下相近，对地峰值力降低了5.8%，落地冲击有效峰值力降低42.5%。阻尼缩小100倍时，跳跃高度增加了6.9%，跳跃距离增加了6.9%，起跳时对地作用力曲线与初始阻尼条件下几乎重合，落地冲击有效峰值力升高15.3%。

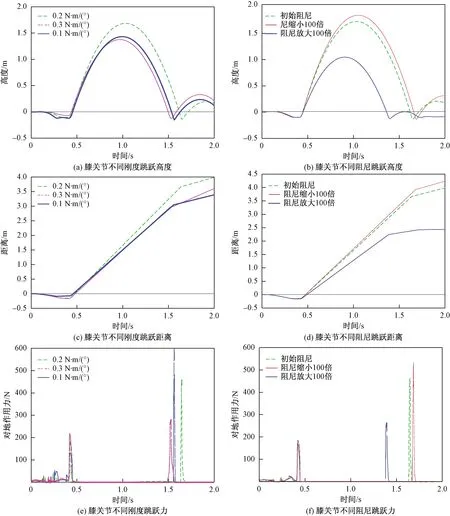
图8 膝关节弹性环节刚度和阻尼不同配置下仿生腿机构跳跃效果对比曲线Fig.8 The jump effect comparison curves of bionic leg mechanism under different configurations of stiffness and damping of elastic element of knee joint

由于输入力矩大小及作用时长不变，其他参数不变，膝关节弹性环节刚度增大则无法达到腿机构最大行程，刚度减小则同样行程内储存能量减少，因此跳跃高度和距离均减少。一定范围内，刚度越大起跳时对地作用力时间越短，对地峰值力越大。膝关节弹性环节阻尼越大，能量消耗越大，则跳跃高度和距离均减小，阻尼增大或减小对起跳时对地作用力无显著效果。膝关节弹性环节刚度及阻尼的增大均能有效吸收腿机构落地冲击。

从图9可知，保持输入力矩大小及作用时长不变，其他参数不变，趾关节弹性环节刚度放大100倍时，跳跃高度增加了11.7%，跳跃距离减少了44.6%，起跳时对地作用时长与初始刚度条件下相近，对地峰值力增大了1.7%，落地冲击有效峰值力降低6.4%。刚度缩小100倍时，跳跃高度、距离、起跳时对地作用力曲线均与初始刚度条件下几乎重合，落地冲击有效峰值力升高7%。趾关节弹性环节阻尼放大100倍时，跳跃高度减少了1.6%，跳跃距离增加了0.8%，起跳时对地作用力曲线与初始阻尼条件下相近，落地冲击有效峰值力降低16.8%。阻尼缩小100倍时，跳跃高度减少了0.4%，跳跃距离增加了0.9%，起跳时对地作用力曲线与初始阻尼条件下相近，落地冲击有效峰值力升高10.7%。

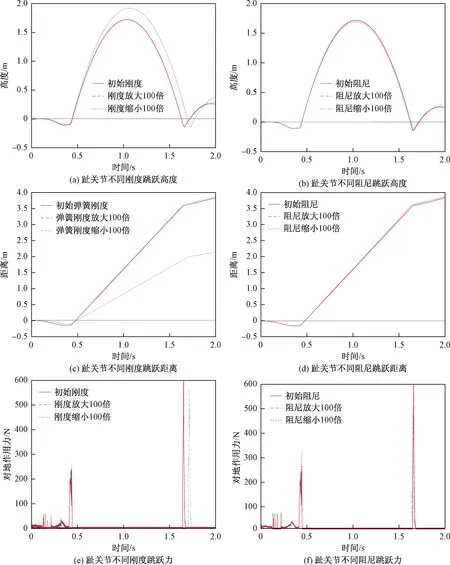
图9 趾关节弹性环节刚度和阻尼不同配置下仿生腿机构跳跃效果对比曲线Fig.9 The jump effect comparison curves of bionic leg mechanism under different configurations of stiffness and damping of elastic element of toe joint

在一定范围内增大趾关节弹性环节刚度，能够使仿生腿跳得更高更近，即一定程度改变其起跳角度，刚度减小则对仿生腿的跳跃效果无显著改变，趾关节弹性环节阻尼放大或缩小，均会使跳跃高度小幅度下降和距离小幅度减小。

趾关节弹性环节阻尼和刚度的改变对起跳时对地作用力无显著改变，增大刚度或阻尼同样能有效吸收腿机构落地冲击。

2.3 根据功率放大对跳跃效果的分析

根据前面对起跳中的输入、输出功率及功率放大因子的计算方法，由于改变各关节弹性环节刚度和阻尼对机构起跳时对地作用力均无显著改变，对2.2.1节仿真的功率过程进行计算，如图10所示。

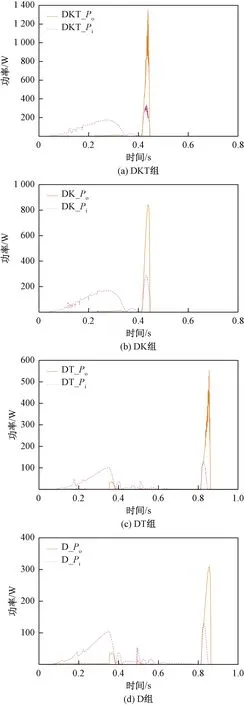
图10 各组输出功率与输入功率Fig.10 Output power and input power of each group

常识上，如果是纯刚性系统，在忽略传输损耗和机构原件消耗的能量下，系统的输入输出功率应该同步且相等，这是我们推导刚性系统力学的基础，比如虚功原理。但在图11中，可以发现，该机构的几种配置方案的输入、输出功率既不同步也不相等。共同的趋势是，在起跳前，尽管有较大的输入功率，但输出功率非常小。在起跳时的较短时间内(约为0.2 s)，输出功率达到一个非常大的峰值，输入功率在此时虽然也有一个峰值，但远小于输出功率峰值。其中峰值时间和大小的差异变化过程说明，弹性元件可以在起跳前将电机的输入功大量储存为弹性势能，在起跳时瞬间释放，以获得一个较大的起跳瞬时功率，形成时间上的能量调度和功率调制。鉴于在没有弹性元件下这个系统很难跳起来，可见系统中弹性元件的存在形成的这种功率放大，对于机构的跳跃能力来说是关键因素。

计算各对照组的跳跃功率放大因子，如表3所示。由四组配置的功放因子可以看出，功率放大均在二倍以上。其中跳跃效果最好的DKT组的C值接近4倍。但在表中也发现跳跃效果不是最好的DT组的C值达到最大，为4.27倍。其中原因有待研究。但是，对照功率图可以看出，尽管DT组的功率峰值较高，但其波形尖锐，包容面积较小。对其积分得到的做功值必然较小。这应可以解释其C值虽然较大，但跳跃效果并非最好。

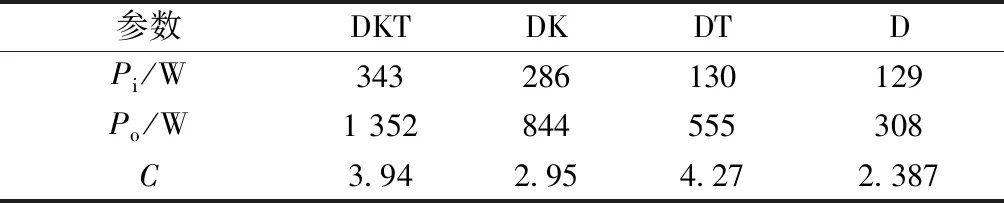
表3 峰值输出、输入功率及功率放大因子Table 3 Peak output, input power and power amplification factor

DK组的C值为2.95，D组为2.39，可见加入K后功放的放大提高较明显。二者波形均比较光滑，变化均匀。比较DKT、DK和DT组波形，发现，DKT的波形基本上就是在DK波形的基础上叠加上DT中较尖锐的那部分波形。波形包络的主要面积还是DK的那部分波形。这也说明尽管增加T可以大幅提高峰值功率，但其在跳跃中的贡献还是有限。以上分析对跳跃机构设计的启发是，应该追求波形较为厚实的功率放大效果，而不是一味追求提高功放因子。

该机构设计中，尽管T配置对跳跃能力提高效果不彰，但在尽可能挖掘一切有助于跳跃提高的原则下，还是应该利用的。况且，在真实样机设计中，为跳跃机构的站立稳定起见，需要考虑设计足趾，使具有一定的支持面积，这个具形的足趾必须采用柔性连接方式。这个问题可留在实际设计时考虑。

2.4 仿真运动过程与实猫实验数据的比较

图11所示为腿机构跳跃仿真过程中各关节转角曲线，图12为实验模本所用猫单次跳跃过程中各关节转角曲线，该过程大约与图11中0.3～0.45 s时间段对应。其中，髋关节曲线均为最先攀升，膝关节和踝关节随后攀升，踝关节转角范围均略大于膝关节，髋关节转角范围最小。可见仿生腿机构跳跃运动过程与所用模本猫跳跃实验实验过程趋势一致，二者在运动方式上具有一定相似性，对机构的研究可作为在猫生物机构跳跃研究中的镜鉴。

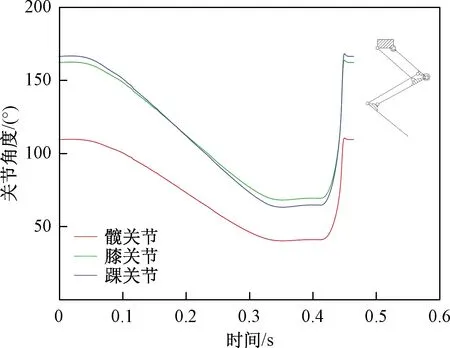
图11 仿生腿机构跳跃过程各关节转角曲线Fig.11 The rotation curve of each joint during the jumping of bionic leg mechanism

图12 猫跳跃实验过程各关节转角曲线Fig.12 The rotation curve of each joint during the jumping of the cat

3 结论

针对所设计的仿猫后肢跳跃机器人机构的跳跃能力进行了研究。

机构的构型和参数按照猫后腿的骨骼形式和测量参数设计。对其运动学模型进行了分析。在此基础上对其跳跃能力进行了仿真实验和分析，目的是研究柔性原件在机构中形成的刚柔耦合作用对机构跳跃能力的影响。

在ADAMS的运动仿真中，对在髋关节、膝关节和足趾部分布置的弹簧的不同配置方案对跳跃的影响进行了分析。得出弹性元件，在与机构的运动耦合中，通过蓄能作用，并在跳跃瞬间的释放，形成高倍数的功率放大作用，形成非常高的瞬时输出功率，从而与地面产生较大的接触力，产生较高的加速度，实现较大的起跳瞬时速度，从而达到提高起跳效果的作用。对机构的功率输入输出曲线分析表明，在机构起跳前，尽管电机输入大量的能量，但机构输出功率很小，说明此阶段输入功率大部被弹性元件吸收为势能。而在起跳阶段，相对于功率输入曲线，机构产生很高的瞬时输出功率，和较大的功率曲线包络面积，说明蓄能原件的做功是跳跃能量的主要部分。以上分析说明了由于柔性蓄能元件与刚性主体机构形成了刚柔耦合机制，在跳跃中形成了功率放大的效果，使机构获得较好的跳跃能力。

比较不同的弹性原件配置效果发现，配置在髋关节和膝关节的弹性元件对跳跃能力提高作用明显，而在足趾部分，尽管弹性元件可以产生很大的峰值功率，大幅提高功率放大因子，但是总的做功不多，对跳跃能力提高的贡献较小。

文中同时对机构中各个关节的阻尼、刚度配置的不同对跳跃能力的影响进行了简要的仿真和分析。

以机构跳跃中各关节角位移轨迹与猫跳实验的数据作比较，发现二者有近似的过程趋势，说明其机构运动特点相近，因此对其的研究也可在对猫的运动能力研究中作为参照。