面向任务的装备维修保障资源配置研究

吴 莹，彭轶轩，郑婉文，徐成成，周献中,2，冯少冲

（1.南京大学工程管理学院，南京210093；2.南京大学智能装备新技术研究中心,南京210093；3.陆军工程大学石家庄校区装备模拟训练中心，石家庄050003）

装备维修保障是为了使装备保持、恢复、改善规定的技术状态实施的全部活动［1］，维修保障资源是其重要组成部分。装备维修保障资源是指维修装备需要的物质资源、人力资源等各类资源的统称，是构成装备维修保障系统的重要基础。其中，维修物质资源主要指装备实施维修所需消耗、补充的各种物质资源，如备件、原材料，以及所需的工具、设备、设施等。维修人力资源主要是指实施装备维修保障的各种相关人员，包括人员的数量、专业特长与技术等级。装备维修保障过程中涉及大量的资源，如何合理地调度与优化维修资源，使维修资源充分发挥作用，是装备维修保障所必须解决的一个重要问题。

随着装备技术复杂程度增加等因素影响［2⁃4］，装备使用的复杂性和专业性越来越强，装备维修频繁等问题越来越明显，装备的完备性受到显著影响。目前军队管辖的武器装备众多，而维修保障资源有限，装备资源分配和调度面对的困难和挑战越来越多。

面向任务的资源维修配置方法是一种新型的维修资源配置方法，主要是针对具体维修任务，在确定的任务需求及资源供给的条件下优化资源配置方案，更适用于战争环境［5］。在未来信息化战场上，面对具体维修任务，资源快速调度与配置需求十分迫切，合理调度维修资源、制定维修方案、恢复装备战斗力是要解决的关键问题，因此本文重点研究面向任务的装备维修保障资源配置问题。在新形势下，面向任务的维修资源调度优化技术水平是衡量装备战斗力和完好性的重要因素。

很多专家学者对装备维修保障开展了研究。郭小威等建立了一种最大化任务可用度的非线性整数规划模型［6］。于风竺等开展了根据任务的优先级进行面向任务的舰船装备维修保障资源优化配置研究［7］。冉悄然等以维修人员为对象，研究了面向复杂任务的装备修人员仿真评估［8］。

针对资源与任务匹配方面，很多学者也开展了相关研究工作。何巍等在服务架构理论基础上，构建了云制造多任务调度流程［9］。Levi等以最小化维修费用为目标构造了针对空军飞机模块化系统的维修任务调度模型及算法［10］。Safari等针对流水车间机器维修任务调度提出了多目标函数动态抢占调度的思想［11］。Zhu等提出了一种基于E⁃CARGO的资源配置模型，对基于角色的协同问题开展了研究工作［12⁃13］。

以上学者对面向任务的装备维修及资源调度问题开展了丰富的研究工作，但是对面向任务的装备维修保障资源配置方法多数具有一定局限性，如何便捷、高效、合理地为装备维修任务匹配资源依然是目前需要研究的重点问题。

遗传算法［14］是一种应用非常广泛的智能算法，其主要思想是基于达尔文进化论与孟德尔遗传学说，通过让种群“优胜劣汰”，模拟大自然适者生存的自然法则，来在可行空间中搜索最优解。遗传算法具有强大的全局最优搜索能力、良好的信息处理能力，并且具有较好的鲁棒性和适应性，因而成为一种应用非常广泛的求解方法［15］。

本文主要针对面向任务的装备维修保障资源配置问题，在对维修任务进行系统描述和分解的基础上，构建了面向维修任务的资源配置模型，并通过遗传算法进行合理、有效求解，同时在遗传算法设计上嵌入了有限选择的随机替换模块，避免了维修资源的重复分配。对于未来信息化战场上的装备维修资源保障辅助决策提供了重要参考。

1 装备维修保障资源配置建模

1.1 问题分析

资源配置是装备维修保障的重要组成部分，装备维修保障资源调度是装备维修保障作业实施的基本依据，需要统筹安排资金、场地、器材、人员等大量资源，对快速修复故障设备、恢复军队战斗力具有至关重要的作用。本文着重考虑战时状态下面向任务的装备维修保障资源配置问题。

维修任务是指为使装备恢复正常使用能力而采取的相关作业的组合。面向任务的装备维修保障建模需要根据装备的故障情况和使用需求自上而下进行任务分解，逐步从整个装备的维修任务分解到具体进行维修操作的原子任务，建立全装备任务层次模型，分解过程如图1所示。原子任务为可调用维修资源的最小单位。整个维修任务分解的层级根据不同的维修部件可能会有所差别，有的维修任务可直接分解为原子任务，有的可能要进行多个层级的分解才可以分解到原子任务。

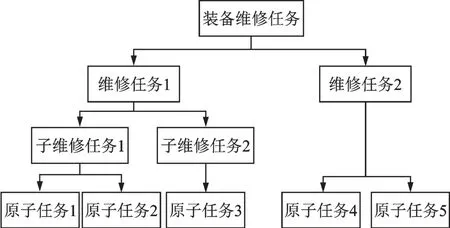
图1 面向任务的装备维修保障模型分解图Fig.1 Decomposition diagram of task-oriented equipment maintenance support model

维修任务可能是多样的，所需要的器材、备件、场地和维修人员可能也不尽相同，原子任务确定以后，与之匹配的维修资源也确定下来。考虑到装备维修现实情况，维修资源往往是有限的，一个资源可能可以服务多个原子任务，也可能只能服务于一个原子任务。例如同一个维修队，既可以维修发动机，也可以维修液压器，而另一个维修队只能维修液压器，没有能力维修发动机。同一资源在不同任务上发挥的效益可能存在差异，例如一个技术人员可以快速地维修好发动机和维修液压器，另一个维修人员维修液压器效果很好，维修发动机可能会很慢。在此条件下，如何进行资源的优化配置，使维修保障整体工作取得最高的效益是亟需解决的重要问题。

装备维修保障资源优化配置过程中，需要以配置方案综合效益最高为目标，充分考虑到资源与任务的匹配度，通过便捷的方式形成合理的资源调用方案用于装备维修，以快速恢复装备战斗力。面向任务的装备维修保障资源配置问题可以描述为维修任务确定的情况下，任务需求与资源供给的最优匹配问题。

1.2 资源配置问题建模

战时条件下，装备维修的任务应是明确的，本文研究的即是在明确维修任务的情况下，如何高效配置维修资源。维修资源可以是维修的人员、设备、配件等。本文将维修资源编制成资源组，资源组可以只包括一项资源，也可以是几项不同资源的组合。面向任务的装备维修保障资源配置的目的是以最小的代价、最高的效益为维修任务配置资源，该效益可以是维修时间最短、维修费用最低或维修效果最好等，也可以是综合效益。根据以上问题描述及分析，对面向任务的装备维修保障资源配置问题进行建模，为了便于问题描述，本文做出如下定义。

定义1 装备维修任务用字母A表示。假设装备发生故障，因而产生多个维修任务，经过分解，最后需要维修的原子任务有m项，则维修任务集 合 即 为 原 子 任 务 集 合，为A={a1，a2，…，am}。例如在战时状态，一台雷达发生故障，经检查发现其故障部位分别为发动机和显示器，需要维修发动机和更换显示器，进一步检查发现发动机的问题出现在活塞和曲轴箱上，需要对活塞和曲轴箱分别进行维修。则该装备维修任务最后分解为维修发动机活塞、维修发动机曲轴箱和更换显示器3个原子任务。

定义2 维修资源组用字母R表示。针对维修任务，可以有n个资源组用于配置完成任务，则维修资源集合为R={r1，r2，…，rn}。例如在上例中，需要分配人员和器材来对设备进行维修，将每一套维修人员及其所管理的设备组成一个资源组，在军队中往往以维修队的方式开展装备维修工作，则可参考军队的维修队配置分为若干个资源组。如果器材是可以随意取用的，也可仅将维修人员作为资源组进行分配，一个或若干可协同合作的人组成资源组，用于完成维修任务。

定义3 将资源组与原子任务的匹配关系用分配矩阵M表示，矩阵数值用mij表示。对于一个有m个原子任务、n个资源组的装备维修任务，M应为n行m列的矩阵。矩阵取值为0或1，其中mij=0，表示第ri项资源组未分配给原子任务aj；mij=1，表示第ri项资源组分配给原子任务aj使用，分配矩阵M可表示为

定义4 将每个资源组分配给某项原子任务产生的效益用效益矩阵B表示。对于一个有m个原子任务、n个资源组的装备维修任务，B应为n行m列的矩阵，矩阵数值用bij表示。根据装备维修现实情况，所有效益值均取非负值，取值为0表示该资源组不能用于相应的维修任务，数值越大表示该任务调用相应资源的效益越好，效益矩阵B可表示为

对于一组维修任务分配的资源，根据维修效益的不同类型，可能有不同的效益矩阵。例如可以将维修的时间、费用、效果等各项维修效益因素合并考虑，用综合效益矩阵B表示资源分配后综合维修效益。也可仅考虑维修时间效益，则有对应维修时间效益矩阵B1；仅考虑维修费用效益，则有对应维修费用效益矩阵B2；仅考虑维修效果效益，则有对应维修效果效益矩阵B3。

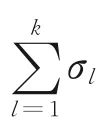
在装备维修保障原子任务产生后，需要调用资源完成相应的任务，则完成维修保障任务的最大效益值为

F即为装备维修保障资源配置的总收益，式（1）则为该模型的目标函数。

本文假设每个任务调用一种资源组，考虑到军队维修实际情况，每个资源组同一时间只能用于完成一项任务，所有资源组不必全部被调用，且为保证所有任务都有资源与其匹配，资源组数量应不少于任务数，则有以下约束条件

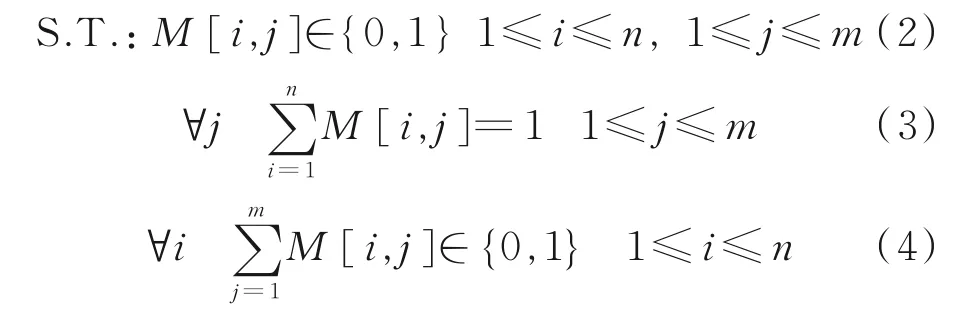
2 基于遗传算法的装备维修保障资源配置模型求解

2.1 遗传算法总体思路

本文采用遗传算法求解以上问题。首先找出并保留最优个体，然后基于轮盘赌的形式选择优良个体，再对种群染色体进行交叉和变异，直至循环到设定的迭代次数。基于轮盘赌的形式可以使适应度值大的个体有更大概率能被选择作为父代个体来生成新个体，有利于保留种群中的优良个体。在算法运行过程中，每次迭代都将最优个体保留，有利于种群快速优化。

在本文中，为了更加高效解决资源配置的实际问题，采用了实数编码的方式，种群中的每一个染色体表示一种资源组分配方案，染色体长度等于原子任务数量。实数编码避免了编码和解码的过程，在任务数量及资源组数量比较多的情况下，实数编码的方式使遗传算法更接近问题空间，能够有效提高算法运行效率。

在算法设计过程中，考虑到战时实际状态，每个资源在同一时间内不应该配置给不同任务使用，因此在算法设计中嵌入了有限选择的随机替换模块，在每次交叉、变异结束后，对资源的重复利用情况进行判定，将重复分配的资源替换成为未被分配过的资源，且每个资源仅分配给一项任务，再进行下一轮的基因选择。通过这一方法有效避免的资源的重复分配，提高了资源配置的合理性和完成维修任务的整体效能。

2.2 遗传算法详细设计

2.2.1 种群设置

遗传算法采用种群搜索技术，种群代表一组问题解，种群中的每个集体即为一个可行解，每个个体为一条染色体。种群数量的多少代表初始设定的个体数量的多少。种群数量太小，不能提供足够样本进行遗传，不利于快速寻优；种群数量太大会增加计算复杂度。一般种群取值在10～200之间。

个体染色体编码时，首先分解装备维修任务至原子任务，并对原子任务进行编号，原子任务集合为A={a1，a2，…，am}。再 对 维 修 资 源 组 进 行 编号，维修资源组集合为R={r1，r2，…，rn}。将每组任务序列分别调用的资源组序列作为遗传基因，采用实数编码的形式，则种群染色体为C={cij|1≤i≤N，1≤j≤m}，其中N表示初始种群中染色体个数，m为维修任务数，cij为第i条染色体的第j个基因，其数值为第j个维修任务调用的资源组编号。

2.2.2 适应度函数

在遗传算法中，适应度函数是用来衡量一个解的好坏的，适应度函数一般是由目标函数线性变换得到的。本文以调度效能最优作为优化目标，因而采用个体目标函数值作为适应度值，适应度值越大说明资源配置方案的整体效能越好。

2.2.3 选择操作

选择操作是将适应度值高的个体以一定的概率遗传到子代，其作用是避免有效基因的缺失，使高性能的基因遗传到子代的概率更大，从而提高算法的全局收敛能力和运算效率，本文采用轮盘赌法来进行选择操作。首先产生N个［0，1］之间的随机数，并顺序排列，然后利用个体适应度值计算每个个体被选择概率的累积和，与之前产生的随机数进行比较，个体适应度值大小代表了被选择的概率大小，个体适应度越大就越容易多次选中并保留；相反，个体的适应度值越小，被选择的概率越小，越容易被淘汰。同时在本算法中引入精英保留策略，将父代种群中最优的染色体直接放到子代种群中，被选择的精英个体直接进入下次迭代，此种方式可以有效避免精英染色体的丢失，加快种群的收敛。

2.2.4 交叉操作

交叉操作是将群体中选中的两个个体中的部分基因进行交叉重组，从而产生新的个体。通过交叉可以提高遗传算法的搜索能力。交叉率为0～1之间的数，较大的交叉率可以增强遗传算法开辟新的搜索区域的能力，但群体遭到破坏的可能性也比较大，交叉率太小会使种群过于迟钝，均不利于搜索最优解。一般交叉率设置在0.25～1之间。

2.2.5 变异操作

变异操作是随机选取一部分染色体上的部分基因，改变为其他的等位基因，变异可以保持群体的多样性。变异率设置较低可以防止群体中重要基因的丢失，变异率设置较高将使遗传算法趋于纯粹的随机搜索，不利于寻优操作，所以变异率的选择不宜太高，一般在0.001～0.1之间。

2.2.6 遗传算法流程

本文中的遗传算法流程如图2所示，其具体步骤如下。

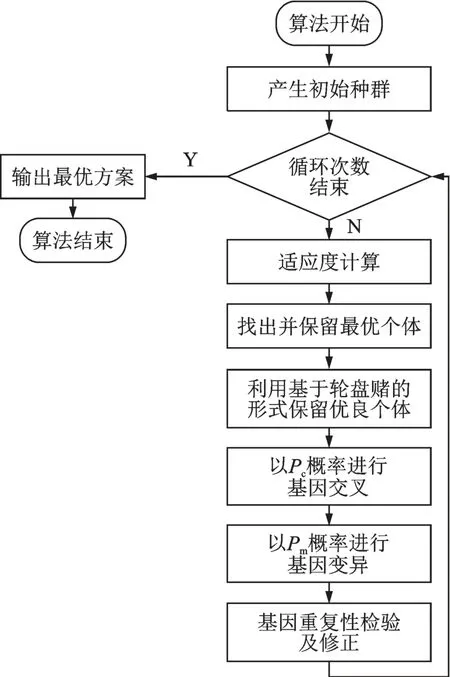
图2 求解装备维修资源配置方案的遗传算法流程图Fig.2 Flow chart of genetic algorithm for solving equip⁃ment maintenance resource allocation scheme

（1）确定初始值。确定群体个数为N；基因长度L为原子任务数；确定交叉率Pc，变异率Pm，迭代次数G，资源组数量Num。

（2）开始迭代，计算适应度。计算出每条染色体的适应度值，适应度值为目标函数值。

（3）记录适应度最高的个体，并保留。

（4）筛选优良个体。基于轮盘赌的形式进行选择，将较为优良的个体保留在种群中，不良个体大概率被剔除掉。

（5）交叉。以Pc的概率随机选择交叉的染色体，对每对相邻染色体偶数位基因进行交叉操作。

（6）变异。以Pm的概率对染色体进行变异，每条染色体的变异率也为Pm。

（7）基因重复性检验及修正。对染色体的基因配置情况进行检验，并对重复基因进行随机不重复替换。将使用过的基因编码用集合X进行标记，未使用过的基因编码用集合Y进行标记，首先在每条染色体进行重复基因替换前，集合Y中基因随机排序，进行替换操作时不再变动集合Y中基因顺序。染色体中如果有重复的基因编码，仅保留一个重复基因，其他基因依次从集合Y中顺序选择一个赋值。

（8）返回第（2）步，重新计算适应度，直至迭代次数达到G。

（9）算法结束，输出最优资源配置方案及适应度值。

计算得到的最优资源配置方案记为Cmax，综合效益最优值为fmax。

3 实例分析

3.1 装备维修保障任务实例

假设在军队演练过程中，有1台装备发生故障，产生维修任务需求，分解后共产生10个原子任务，现在需要调用人员进行维修。目前有12个人可以开展维修工作，每项原子任务需要派一个人来完成。则每个维修人员即为一个资源组，每一项原子任务都需要有相应的资源组与其相匹配。在本例中，原子任务编码为1～10，资源组编码为1～12，在综合考量维修时间、维修质量和维修成本的基础上，每项资源组完成原子任务的综合效益矩阵如表1所示。

表1 实例中维修任务对应资源组的效益值Table 1 Benefit values of the maintenance task corre⁃sponding to the r esource group in the example

根据以上实例，可得到维修效益矩阵为

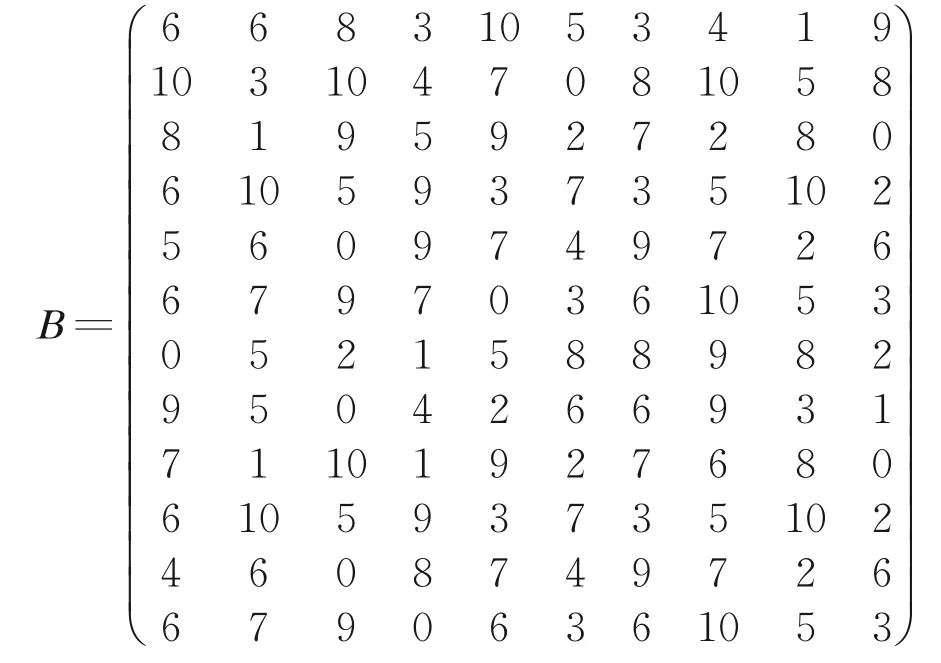
3.2 算法实现

3.2.1 实验设置

根据上文设置的实验算法和实验数据，应用遗传算法求解最优资源配置方案。本案例中，基因长度L=10，每个基因取值范围为1～12。将种群大小设置为N=200，交叉率为Pc=80%，变异率为Pm=1%，迭代次数为G=200。根据完成每个维修任务调用资源效益值运行遗传算法寻优可以得到最优维修策略为：Cmax=［2，4，9，5，3，7，11，12，10，1］，综合效益最优值为fmax=94，迭代曲线如图3所示。

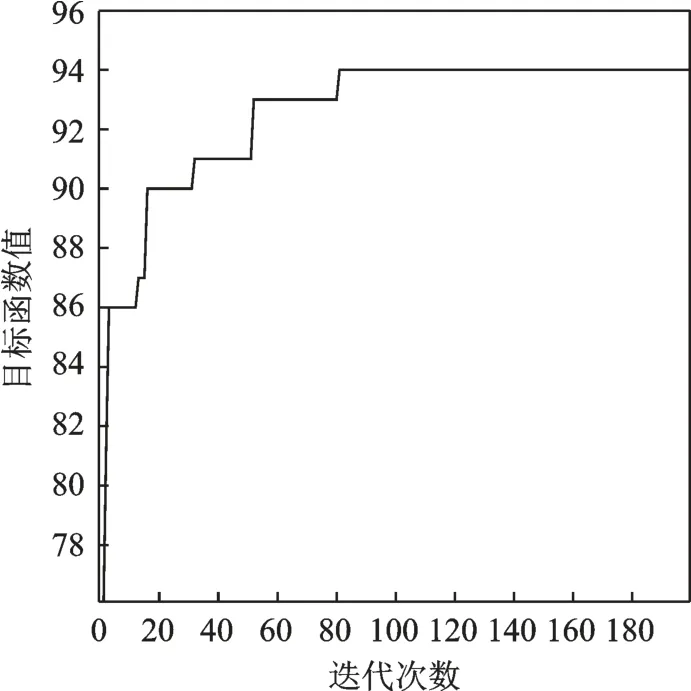
图3 遗传算法运行后的适应度变化曲线Fig.3 Fitness curve of the genetic algorithm after operation

3.2.2 算法效能分析

（1）迭代次数对适应度的影响。

遗传算法的迭代次数的选择是对计算效果和计算时间权衡的结果。本节讨论更改遗传算法迭代次数对运算结果的影响，分别取不同迭代次数，记录运行后适应度值，每组运行50次取平均值，其他实验条件与3.2.1节一致，结果如图4所示。通过分析可以看出，在迭代达到150次以后，算法得到的种群适应度值基本达到最优值94。

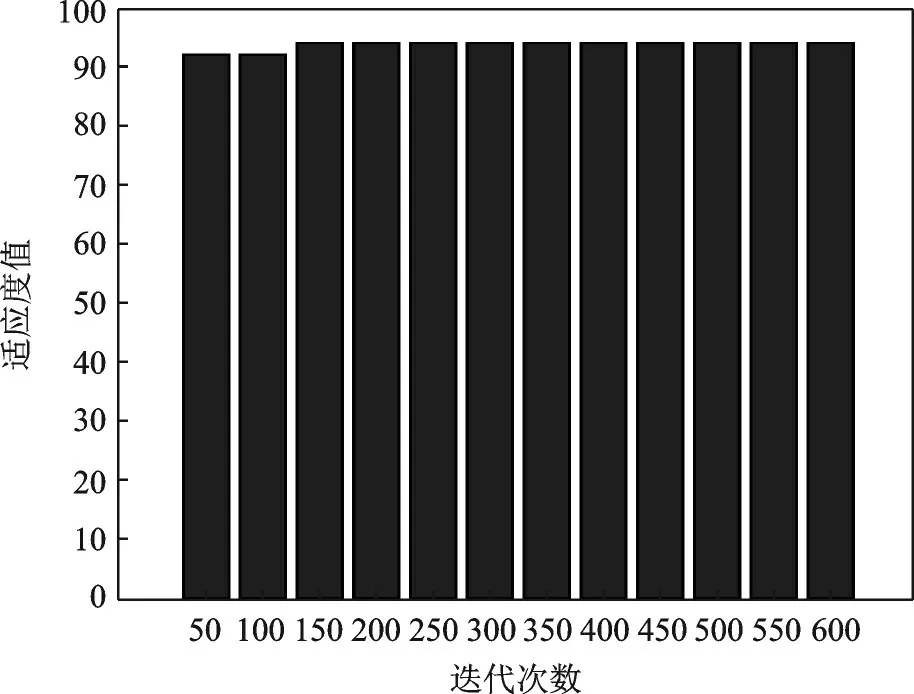
图4 迭代次数与适应度值关系曲线Fig.4 Relationship between the number of iterations and fit⁃ness value

（2）种群大小对适应度的影响

初始种群大小代表了遗传基因是否足够丰富。如果初始种群比较少，则有的优良基因片段可能难以被选中进入下轮的迭代中，或者不能高效获得优良染色体。本节讨论更改种群大小对运算结果的影响，分别取不同种群大小，记录运行后适应度值，每组运行50次取平均值，其他实验条件与3.2.1节一致，结果如图5所示。通过分析可以看出，在种群数量达到150以后，算法得到的种群适应度值基本达到最优值94。

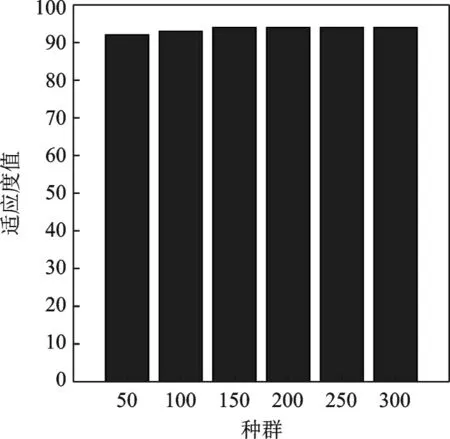
图5 种群大小与适应度值关系曲线Fig.5 Relation between population size and fitness value

（3）交叉率和变异率对适应度的影响

交叉率和变异率对种群的收敛速度、优良基因及染色体的保留也会产生较大影响。本节讨论交叉率和变异率对运算结果的影响，分别取不同交叉率和变异率，记录运行后适应度值，每组运行50次取平均值，迭代次数100次，其他实验条件与3.2.1节一致，交叉率对适应度的影响如图6所示。由图6可看出，交叉率越高越容易得到适应度较高的值，交叉率达到0.4以后适应度值基本稳定。

图6 交叉率与适应度值关系曲线Fig.6 Relation between crossover rate and fitness value

变异率对适应度的影响如图7所示。由图7可看出，变异率越高越容易得到适应度较高的值，变异率达到0.06以后适应度值基本稳定。

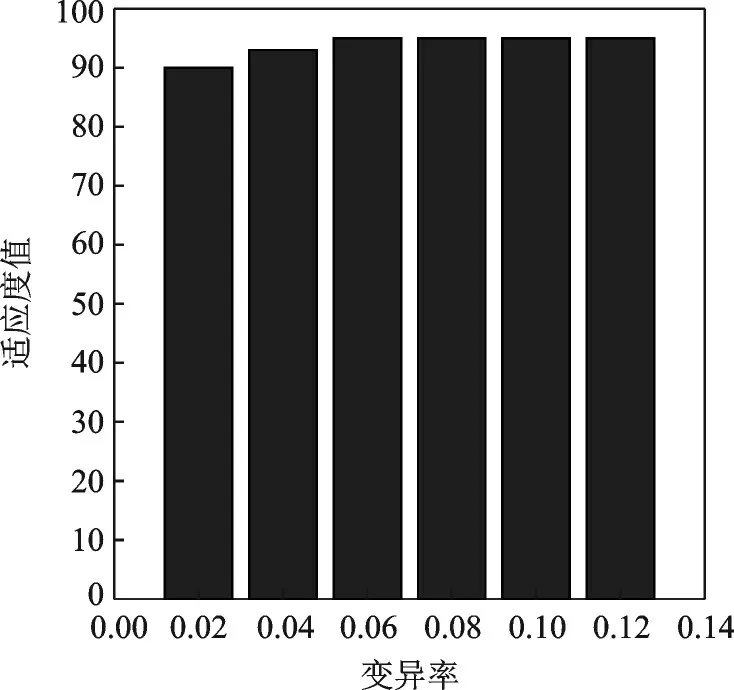
图7 变异率与适应度值关系曲线Fig.7 Relation between variation rate and fitness value

（4）多目标情况下实例分析

假设在以上实例中，将时间效益、成本效益、质量效益分开考量，其对应的效益矩阵分别为

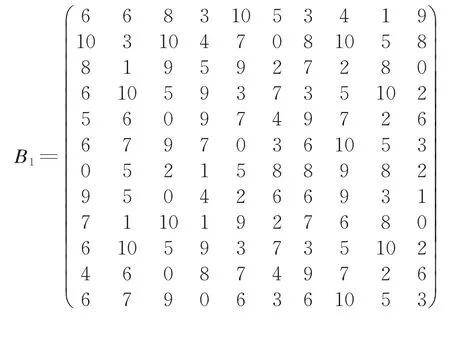
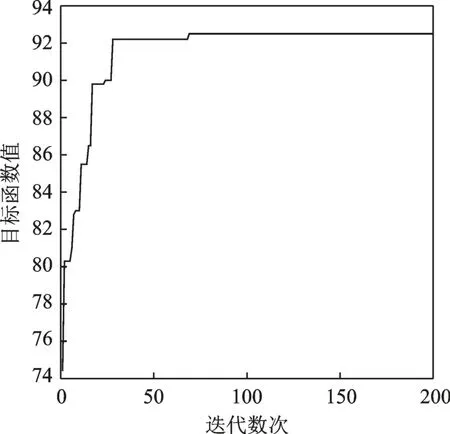
图8 多目标条件下遗传算法运行后的适应度变化曲线Fig.8 Fitness curve of genetic algorithm after operation un⁃der multi-objective condition

通过以上实例可以看出，本文可以很好地解决面向任务的装备维修资源配置问题，并且在多目标条件下也依然适用，可以得到良好的配置方案，该实例仿真结果验证了本文提出的模型算法的有效性和可行性。

4 结 论

本文对面向任务的装备维修保障资源配置问题进行了描述，对维修任务进行了分解，并对资源配置方法进行了研究和建模，通过遗传算法实现了对最优资源配置策略的求解。本文在传统遗传算法的基础上进行了改进，采用了实数编码的形式，使问题空间更加清晰。在算法设计中针对现实情况下资源与任务的唯一性匹配问题，嵌入了有限选择的随机替换模块，传统遗传算法相比，结果更为合理。本文同时研究了多目标条件下的资源优化配置问题，为有效地解决面向任务的装备维修资源配置问题提供了方法，为未来信息化战场上面向任务的装备维修资源保障辅助决策问题提供了重要参考。