吸气式高超声速飞行器预设反演鲁棒控制

王鹏飞，罗 畅，刘承君，张 峰，章 华

(1 陆军炮兵防空兵学院，合肥 230031；2 78092部队，成都 610000)

0 引言

吸气式高超声速飞行器(air-breathing hypersonic vehicles，AHV)是一类以超燃冲压发动机为动力，可在20～100 km空间范围内以速度大于5Ma远距离飞行的新型飞行器[1-3]。但是，由于AHV具备诸多与传统低空慢速飞行器显著不同的动力学特征，使得其控制系统的设计十分困难。美国研制的X-43A高超声速验证机首次试验就因控制系统无法满足预设轨迹跟踪要求而失败。因此，设计满足性能要求的控制系统对我国AHV的发展十分关键。

目前，已有多种控制方法应用于高超声速飞行器的控制器设计，如增益调度控制[4]、反馈线性化控制[5]、滑模控制[6]和反演控制[7-9]等。其中，反演控制方法由于对严格反馈非线性系统具有良好的处理能力，因而已成为AHV主流的控制设计方法。文献[10]在反演控制的框架下，引入自适应滑模控制提升鲁棒性；文献[11]基于微分器设计干扰观测器来补偿模型中的不确定项；文献[8]和[12]分别将模糊控制、神经网络控制与反演控制相结合，有效提高了鲁棒性。

上述研究基本只考虑闭环系统的稳定性，而对控制器的瞬态性能如超调量和调节时间等指标未做约束。基于文献[13]和[14]提出的预设性能控制方法，文中提出一种预设性能反演鲁棒控制方法，实现对飞行器控制系统的瞬态性能约束。通过引入预设性能函数对速度和高度系统的跟踪误差进行转换，从而实现对误差瞬态性能的约束和调整。为提升反演控制的鲁棒性，基于改进的反正切微分器[15]构造一种新型干扰观测器对飞行器模型中的不确定项进行估计。同时，为避免“计算膨胀”问题，引入滑模微分器获取高度子系统中各虚拟导数的估计。最后，通过仿真实验，验证所设计的控制系统能够实现对其瞬态性能的约束。

1 问题描述

1.1 动力学建模

AHV的弹性动力学模型[16]为：

(1)

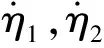
1.2 预设性能

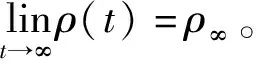
根据文献[17]，预设性能函数可选取为:

ρ(t)=(ρ0-ρ∞)e-lt+ρ∞

(2)

式中：ρ0和ρ∞分别是ρ(t)的初值和终值；l为待设计的正参数。

根据预设性能的定义，系统误差e(t)应满足:

(3)

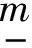
(4)

其中ε(t)为S[ε(t)]的逆函数。则系统误差可表示为:

e(t)=ρ(t)S[ε(t)]

(5)

反解式(4)可得ε(t)为：

(6)

对式(6)求导得：

(7)

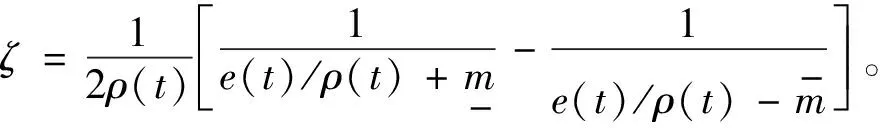
2 控制器设计

根据时间刻度原理[18]，可将AHV动力学模型拆分为速度系统与高度系统分别设计控制器。

2.1 速度控制器

根据式(1)可将速度子系统转换为:

(8)

式中：fV和gV是包含气动力和气动参数的函数；dV为包含弹性扰动的未知项。

(9)

由式(6)设计速度的转换误差εV(t)为

(10)

对式(10)求导得：

(11)

基于动态逆理论，设计速度控制系统的输入Φ为:

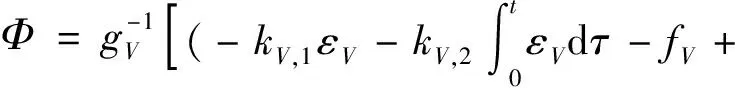
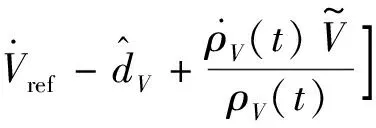
(12)

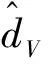
2.2 高度控制器

根据式(1)将高度子系统转换为:

(13)

式中：fγ，gγ，fQ及gQ均是包含气动力和气动参数的函数，dγ与dQ为包含弹性扰动的未知项。

(14)

高度的转换误差εh(t)可表示为：

(15)

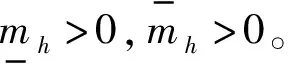
对式(15)求导得:

(16)

选取虚拟控制律γc为:

(17)

式中，kh,1>0和kh,2>0,均为设计参数。

为避免“计算膨胀”，这里引入滑模微分器[19]对γc估计：

(18)

式中，λ11和λ12为待设计参数。

(19)

令虚拟控制量θc为:

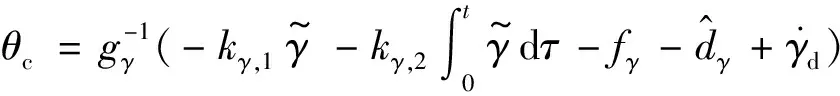
(20)

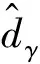
类似的，对θc的一阶导数估计可得:

(21)

式中，λ21和λ22为待设计参数。

(22)

定义虚拟控制量Qc为:

(23)

式中，kθ,1与kθ,2均为大于0的参数。

同样，对Qc的导数估计可得:

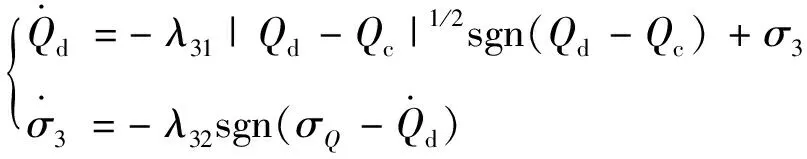
(24)

式中，λ31与λ32为待设计的正参数。定义高度子系统中3个虚拟控制量一阶导数的估计误差为ex=xd-xc,(x=γ,θ,Q)，根据文献[19]可知选择合适参数能保证ex有界，即一定存在大于零的常数ei,M,能够使|ex|≤ex,M,(x=γ,θ,Q)。

(25)

选取高度子系统的实际输入δec为:

(26)

式中，kQ,1和kQ,2为控制器参数。

2.3 干扰观测器设计

为降低模型中不确定项对控制效果的影响，提升反演控制的鲁棒性，基于MATDs[15]构造一种新的非线性干扰观测器对不确定项估计：

(27)

式中:x=V,γ,Q；Rx、bx、lx,1和lx,2均为待设计的正参数。

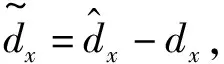
2.4 稳定性分析

选择Lyapunov函数为:

W=WV+Wh+Wγ+Wθ+WQ

(28)

其中

对式(28)求导得:

(29)

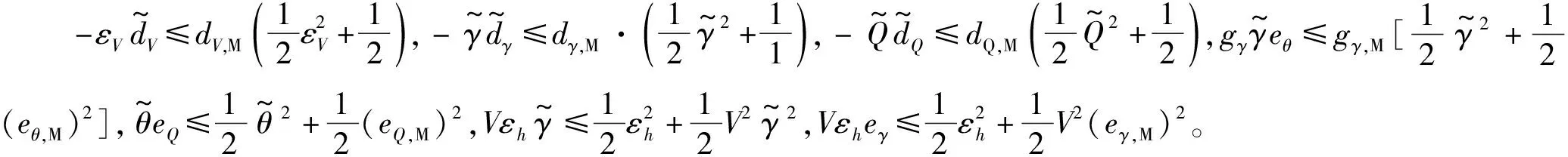
因此可得：

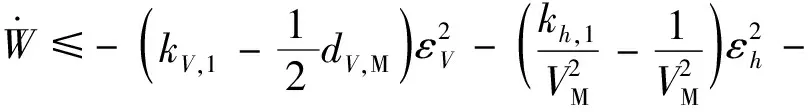
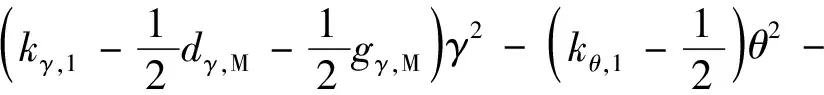
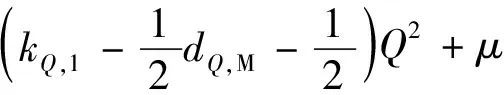
(30)

其中

(31)

(32)

(33)

(34)

(35)

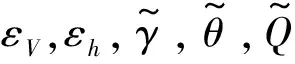
3 仿真实验

基于设计的控制器进行速度和高度参考指令的跟踪仿真，飞行器模型中的所有数据参见文献[16]。控制器参数取kV,1=2,kV,2=15,kh,1=12,kh,2=1,kγ,1=0.3,kγ,2=0.2,kθ,1=0.9,kθ,2=0.2,kQ,1=0.6,kQ,2=0.1;滑模微分器的取值：λ11=λ21=λ31=0.0949,λ12=λ22=λ32=0.0015; 干扰观测器的取值：Rx=5，bx=0.9，lx,1=14和lx,2=15，其中x=V,γ,Q。选取预设性能函数的形式为：

(36)

设定AHV的初始速度V=2346.96 m/s,初始高度h=25908 m。速度参考的阶跃信号为ΔV=500 m/s，高度跟踪的信号为Δh=1000 m。为了验证控制器的鲁棒性，在仿真100～200 s之间，令模型中所有气动参数在±20%之间按正弦规律摄动。此外，在同等条件下将文中算法与文献[11]的方法进行对比，验证所设计控制器的优越性。

仿真结果如图1～图5所示。从图1和图2可以看出，速度和高度的跟踪误差很好地被限制在了预先设定的范围之内。当气动参数发生摄动时，跟踪误差的微小变化不会对飞行器的飞行姿态造成影响。此外，相比文献[11]的结果，文中设计的控制器无论是在控制性能还是鲁棒性方面均有一定的优势。图3为控制输入，可以看到除了在仿真初期有短暂的抖振，整体较为平滑。图4和图5显示飞行器所有的刚体和弹性体状态量能够迅速达到稳定，在存在参数摄动时也能保持在较小范围内变化。

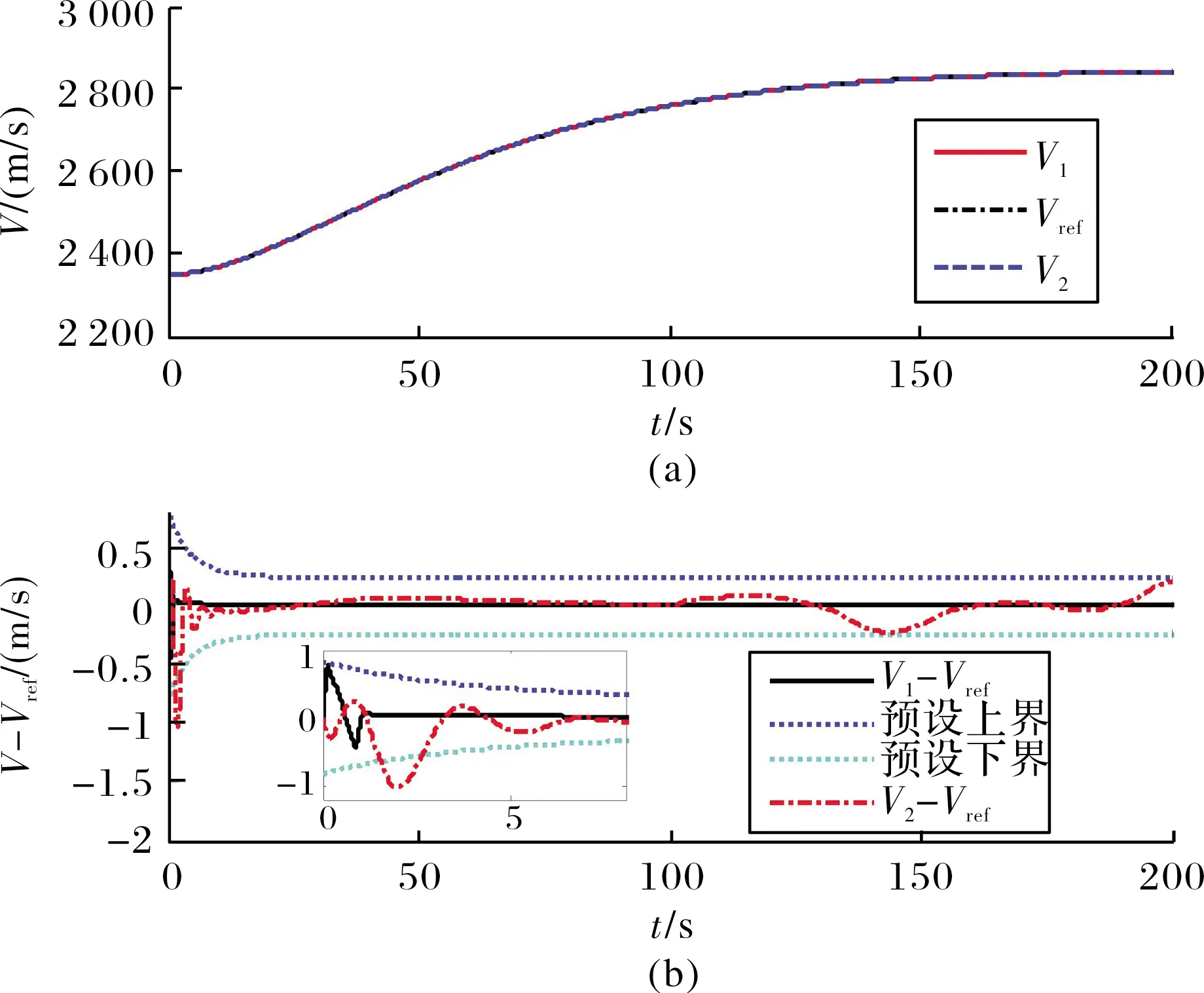
图1 速度及其跟踪误差

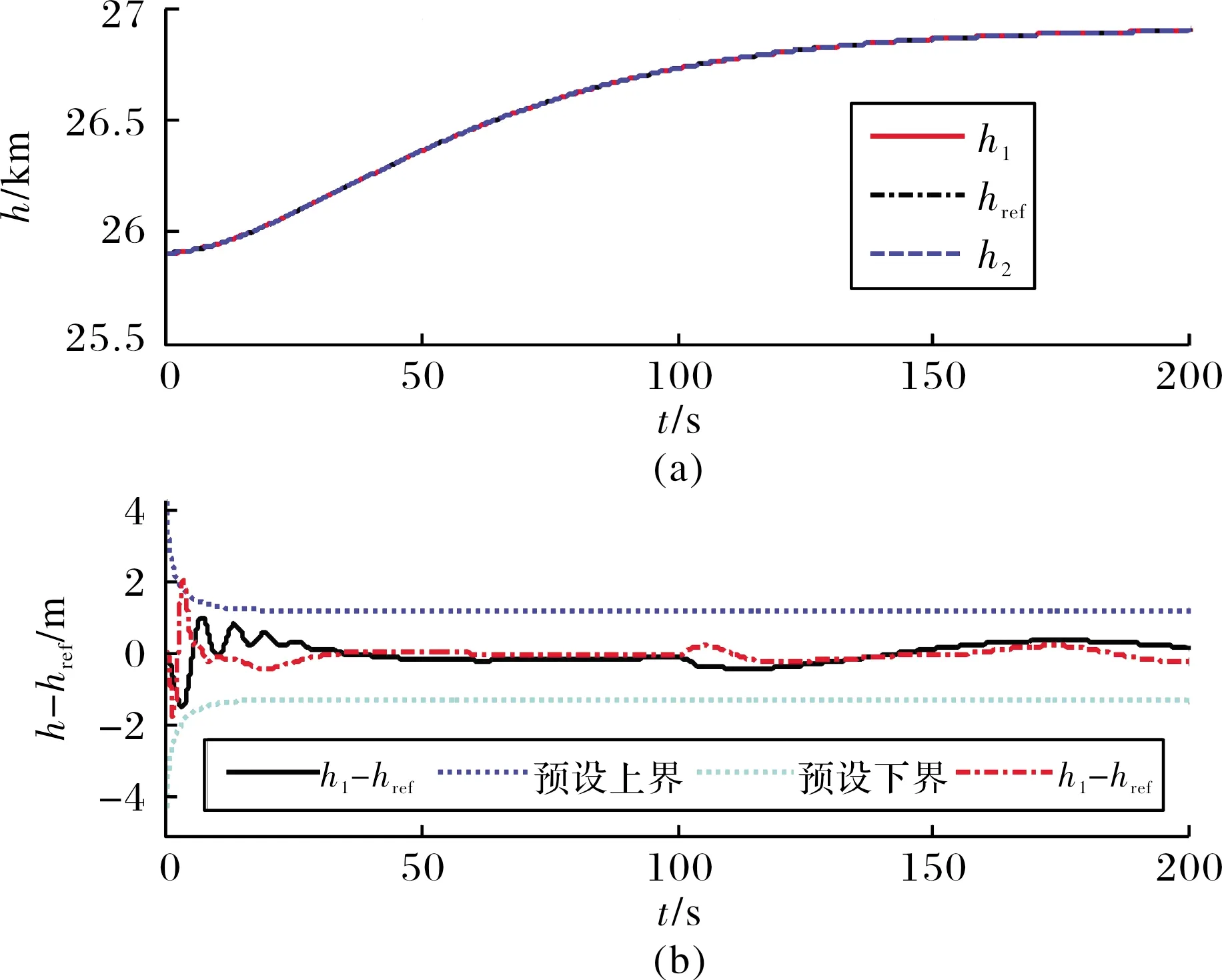
图2 高度及其跟踪误差

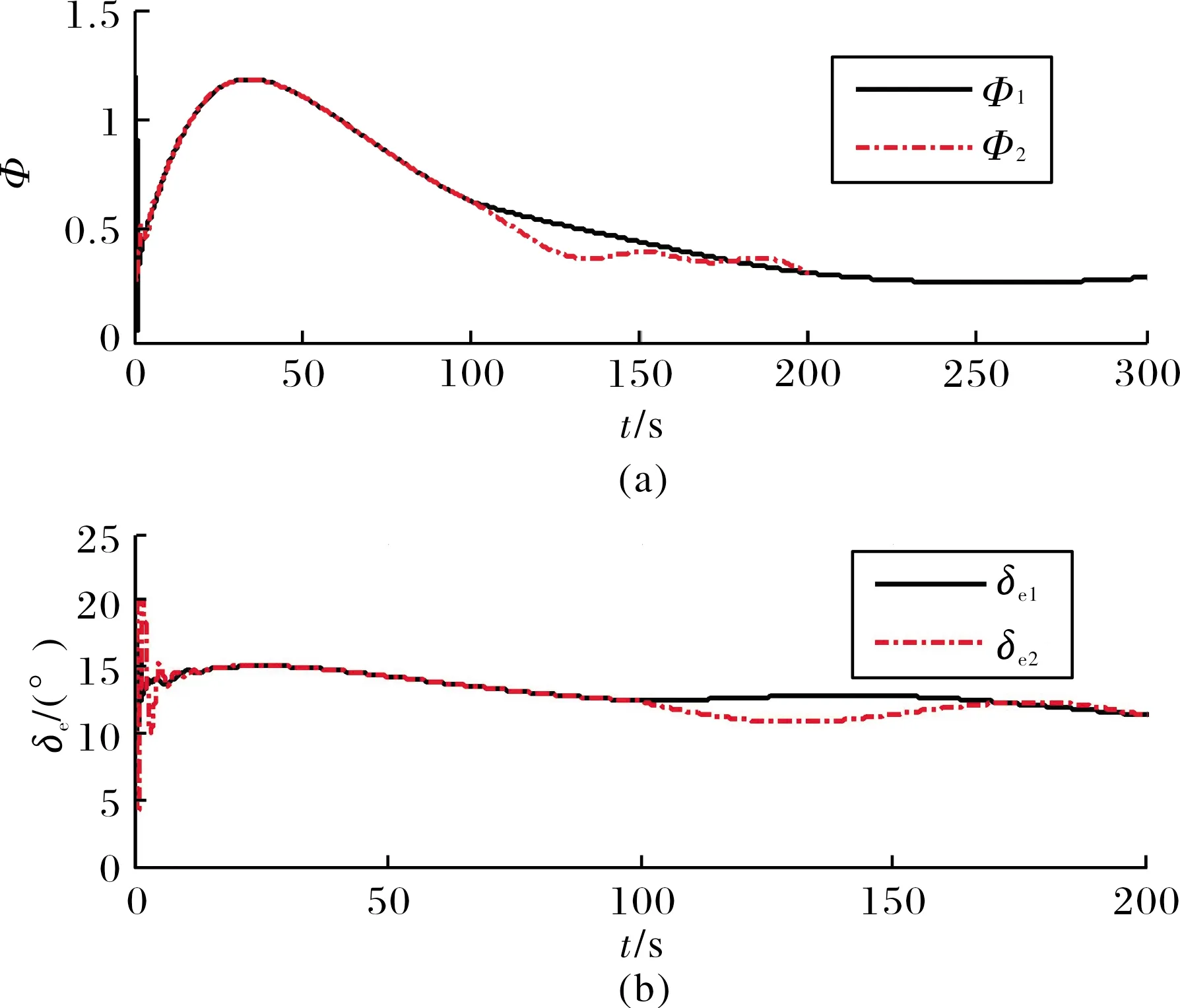
图3 控制输入

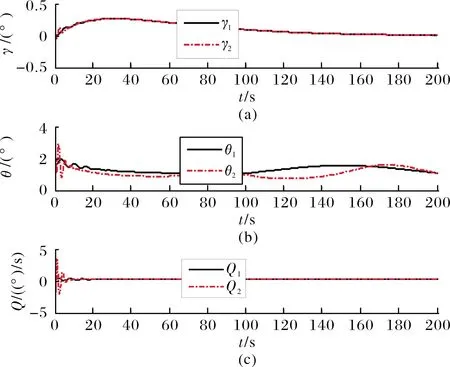
图4 航迹角，俯仰角及俯仰角速率

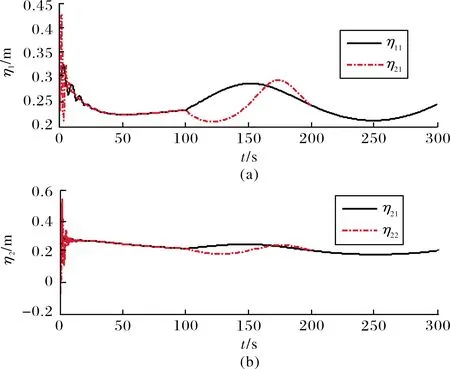
图5 弹性状态

4 结论

设计了一种预设反演鲁棒控制器，能够实现对控制系统跟踪误差瞬态性能的约束。为改善单纯反演控制鲁棒性不高的问题，引入了基于MATDs构造的干扰观测器。通过跟踪轨迹的对比仿真实验可以发现，该控制器具有良好的控制性能，且对气动参数的摄动表现出了较强的鲁棒性。