变质率呈两参数Weibull分布的肉类商品库存管理——考虑库存水平临界点

张 源

（1.上海外国语大学贤达经济人文学院，上海 200083；2.中国社会科学院工业经济研究所，北京 100732）

随着中国供给侧结构性改革的深入落实和市场环境日趋复杂的变化，保持健康高效的库存水平成为诸多企业提升运作管理的重点之一。对经营肉类商品的企业来说，需考虑商品的需求不确定性和易变质性。由于肉类商品效用随时间推移而降低，且产生额外腐坏成本，因此，如何确定肉类商品的最优订货量和订货周期以实现最低库存成本，兼具理论及应用价值。

1963年，Ghare等［1］首次提出变质商品库存模型。之后的50多年，国内外学者结合各类商品提出多种约束条件下的库存模型。Covert等［2］采用两参数Weibull分布函数描述商品变质率；Philip［3］在之后提出三参数Weibull分布的商品变质率模型。随后，Jalan等［4］基于服从两参数Weibull分布的变质率，构建线性需求下的库存管理模型。Chakrabarty等［5］则基于服从三参数Weibull分布变质率的商品，提出相应的库存控制模型。徐贤浩等［6，7］从变质期类型的角度，将变质商品的库存模型分为2种，即固定变质期和随机变质期。有学者将肉类商品归类为固定变质期商品，认为其变质率保持恒定，并在既定时间后效用为0。本研究认为鉴于在仓储过程中受不同温度、气候、湿度和储存方式的影响，商品在库存过程中发生变质的时间和程度是不确定的。现有文献中，随机变质期通常涉及2种变质率类型，即服从时变函数的变质率以及服从Weibull分布的变质率。其中，前者描述随时间推移变质率升高的情况；而后者一般应用于初期变质率较大的情况。本研究认为根据肉类商品的特性，无论是冷鲜肉还是冷冻肉，均应属于服从Weibull分布的变质商品类型，即前期变质速度较快，后期变质速度逐渐放缓，最终商品效用趋近于0，而不同温度下的储存方式决定其变质率的大小程度。与此同时，鉴于肉类商品的变质类型主要指其腐坏过程，即物理性变质，而价值性变质通常只在市场价格大幅波动时或因库存积压而进行折价销售时较为明显，本研究仅考虑商品的物理性变质现象。因此，本研究基于EOQ模型的理论基础，引入库存水平临界点，只考虑库存量低于临界点的情况，结合中国肉类商品销售的运营现状，建立变质率呈两参数Weibull分布的库存管理模型，并进行算例分析，以期为中国当前优化肉类商品供应端提供可行的分析手段和参考建议。

1 问题描述与模型假设

1.1 基本假设

根据对中国部分城市肉类商品销售市场的调研结果，基于单一企业的库存管理问题展开研究，引入如下基本假设条件：a.该公司仅经营一种特定的肉类商品；b.商品发生变质且变质率服从两参数Weibull分布；c.变质过程是不可逆的；d.库存采购提前期为0；e.库存补充速率无穷大；f.不允许发生供货短缺；g.不存在价值性变质。

1.2 符号表示

构建模型涉及符号及定义如表1所示。

表1 构建模型涉及符号及定义

2 模型构建

本研究假设商品的变质率服从两参数Weibull分布。两参数Weibull分布的概率分布函数F（t）和密度函数（ft）分别为：

由式（1）、式（2）可得，服从两参数Weibull分布的变质率：

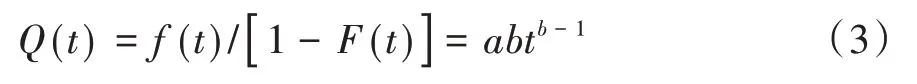
式中，a为尺度参数，0≤a＜1，其中，a=0表示不发生变质；b为形状参数，b≥0。图1是服从两参数Weibull分布的变质率-时间关系。由图1可知，形状参数存在5种情况：①0＜b＜1，变质率与时间变量为负相关，表示变质率在订货周期初期较高，随着时间推移而逐渐降低；②b=1，变质率为常数，变质率与时间变量不相关；③1＜b＜2，变质率与时间变量为正相关，且变质率增高的速率在逐渐降低；④b=2，变质率与时间变量为线性相关；⑤b＞2，变质率与时间变量为正相关，且变质率增高的速率在逐渐增大。本研究结合企业实际运营中大多数物理性变质商品的变质特征，仅考虑b≥1的情况，即变质率随时间的变化逐渐增加。

图1 服从两参数Weibull分布的变质率-时间关系

鉴于部分企业实际经营活动中，往往存在库存水平临界点，一旦随着库存降低并小于临界点时，商品的需求率将保持恒定。根据调研结果，大部分肉类经营企业并不存在面对商品需求随库存降低而显著变化的情况。本研究只考虑库存消耗速度保持不变的情况，即将库存量低于临界点作为假设条件，因此，可以构建模型在Q≤L的条件下，库存消耗速度不随库存降低，消耗率维持在库存临界点时的水平，库存状态方程为：

由I(0)=Q且I(T)=0可得，t时刻的库存水平（5）与最优订货量（6）：

库存变质成本：

库存持有成本：

库存管理总成本：

单位时间库存管理成本：

对式（7）、式（8）、式（9）求导可得：

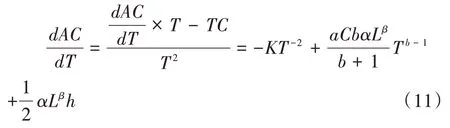
当库存量低于库存临界点的条件下存在最优解T，则存在由式（11）可计算T，式（11）可化简为：

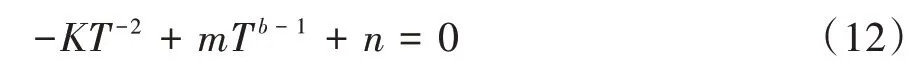
引入函数f(T)且满足：

对f(T)泰勒展开可得：

其中γn(T)为拉格朗日余项：

根据草图发现，y=（fT）与x轴在x=1处附近有惟一交点，取T0=1可得：

现采用反函数多项式展开法，对超越方程进行求解（其中涉及Newton-Raphson迭代法的运用），略去拉格朗日余项后得出二次三项近似式，可作为T的近似解析解：

将T带入式（6）可得最优订货量Q：

本研究仅考虑b≥1的情况，即变质率随时间的变化逐渐增加，也即：

所以，式（21）所得到的T为全局最优解，式（22）所得到的Q即为最优订货量。

3 数值算例与灵敏度分析

3.1 数值算例

算例假设某肉类商品经营企业制定库存管理计划，所经营的商品为单一种类，且物理性变质率服从两参数Weibull分布。库存模型的相关参数如表2所示。

表2 库存模型的相关参数

3.2 求解步骤

将参数值代入式（22）计算，可得最优订货量Q；将Q代入式（6），可得库存补充周期T；将T代入式（7）、式（8），分别可得库存变质成本DC和库存持有成本HC；将DC和HC代入式（9），可得库存管理总成本TC；将TC和T代入式（10），可得单位时间库存管理成本AC。

经过计算，本算例中肉类商品经营企业的最优订货量为6.112 6 t，对应的单位时间库存管理成本为1.931 5万元。

3.3 灵敏度分析

本研究根据算例，通过每次只改变单一参数值，对库存模型中的主要参数进行灵敏度分析（表3）。每次上调或下调参数值的50%或25%，分别可得参数a、b、α、β、K、h、C的变化对最优订货量Q和单位时间库存管理成本AC的影响。值得注意的是在所有计算结果中，最优订货量并未超过库存水平临界点L，因此，计算结果与模型假设并无相悖。

由计算结果可知以下结论：①服从Weibull分布的变质率形状参数b和需求率参数α、β对最优订货量Q和单位时间库存管理成本AC的影响都非常大；②服从Weibull分布的变质率尺度参数a和单位商品变质成本C对单位时间库存管理成本AC的影响非常大，但对最优订货量Q的影响不显著，但两参数对最优订货量Q和单位时间库存管理成本AC的影响同步；③服从Weibull分布的变质率尺度参数a和单位商品变质成本C的变化对最优订货量Q的影响呈负相关，其他参数对Q的影响呈正相关；④服从Weibull分布的变质率形状参数b对单位时间库存管理成本AC的影响呈负相关，其他参数对AC的影响呈正相关。

根据上述结论可以看出，当腐坏速度越快，单位时间库存管理成本越大，企业单次订货量也需要越大，其中，变质的尺度参数对订货量影响较小，而形状参数则对订货量影响较大。此外，市场需求率越大，企业单次订货量也需要越大，单位时间库存管理成本也越大。

表3 库存模型主要参数灵敏度分析

本研究针对影响订货量较大的变质率形状参数b展开进一步分析，将b作为变量，在给定其他参数的条件下，分别可得形状参数与最优订货量和单位时间库存管理成本的关系，如图2和图3所示。

由此可见，当肉类商品的变质率形状参数增加到一定程度时，最优订货量的增长速度（图2）和单位时间库存管理成本的下降速度（图3）均会减弱，切线斜率逐渐趋近于0，即最优订货量逐渐接近一个最高值，而单位时间库存管理成本逐渐接近一个最低值。所以，当肉类商品的腐坏速度超过一个阈值时（本算例中约为b=5），最优订货量将基本不受腐坏速度变化的影响。

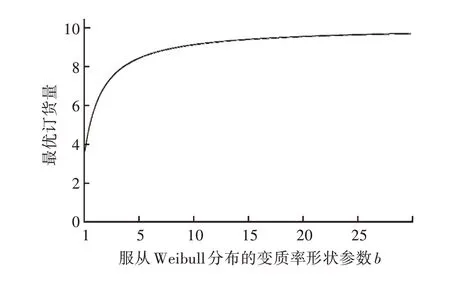
图2 最优订货量-服从Weibull分布的变质率形状参数关系

图3 单位时间库存管理成本-服从Weibull分布的变质率形状参数关系

4 小结

本研究假定肉类商品物理性变质率服从两参数Weibull分布，且不存在物理性变质，在考虑库存水平临界点的条件下，构建肉类商品经营企业的库存管理模型。本研究基于前期市场调研数据，算例参数贴近于现实商业情形，为有效管理肉类商品库存提供学术依据，也为相关企业高质量发展提供智力支持。通过实证发现，商品变质速度对企业的库存管理策略影响较大，变质率形状参数越大，企业单次订货量越大；肉类市场的需求率越大，企业单次订货量也越大。此外，当肉类商品的变质率超过一定程度，最优订货量便不再受变质速度变化的影响。

本研究所构建的库存模型和相关建议同样适用于符合类似物理性变质的其他商品，如水果、鲜切花、超市便当等。现实生活中，节假日等时间节点消费者对肉类商品的需求会大幅增加。因此，市场需求量的大幅波动对物理性变质商品的库存控制影响是后续研究的方向。