外混式喷嘴雾化特性计算机模拟及实验验证

王萍萍，沈 凯，张振东

（上海理工大学 机械工程学院，上海 200093）

0 引言

喷雾是将液体通过喷嘴喷射到气体介质中，使之分散并碎裂成小颗粒的过程［1-2］。由于液体相对于空气或气体的高速运动，液体会雾化成各种尺寸范围的细小颗粒。空气雾化喷嘴为喷嘴的一种，其在化工行业中的雾化降温冷却及粉末干燥脱硫等领域均有广泛应用，并创造了显著的社会效益与经济效益［3］。空气雾化喷嘴的特性很大程度上决定了喷雾锥角的幅度和液滴索特平均直径（Sauter Mean Diameter，SMD）的大小，而喷雾锥角和SMD 是雾化特性的重要指标，因此对空气雾化喷嘴的研究有着重要意义。

国内外学者对空气雾化喷嘴也进行了大量研究，并取得系列成果。文献［4］采用Eulerian-Lagrangian 耦合模型，对内混式空气雾化喷嘴性能进行了数值模拟，得出当气液质量流量比为23%时，距离喷嘴出口20mm 处液滴基本被气流束缚在扇形平面方向上±20mm 的范围内，液滴浓度和速度分布呈“双峰型”分布；文献［5］研究了不同的几何参数，如长径比等对于压力旋流雾化喷嘴的喷雾锥角以及SMD 的影响，在0.8MPa 和1.2MPa 的注射压力下，喷雾锥角随着长径比的增加而不断减小，但对于SMD 而言，长径比的最佳值为3.75；文献［6］通过实验研究了广角内混式空气雾化喷嘴雾滴场的雾化特性，结果表明在宏观雾化特性方面，供水压力和供气压力变化分别对喷嘴的雾化角和射程占主导作用；在细观雾化特性方面，沿轴线方向随着距离增大雾滴粒径不断增大，沿径向方向随着距离喷嘴轴线增大雾滴粒径不断增大；文献［7］研究内混式空气雾化喷嘴的进气孔个数、空气帽出口直径和混合腔长度等结构对雾化特性的影响，4 个进气孔的雾化效果较两个进气孔有显著提高；空气帽出口直径在2.0～3.0 mm 之间时，随直径增大，喷嘴雾滴粒径不断下降。直径继续增大时，雾滴粒径反而稍有增大，雾滴数量也减少；喷嘴混合腔长度可以适当增加，使液相与气相进行充分接触以提高雾化效果。

目前，对于空气雾化喷嘴的研究大多涉及内混式空气雾化喷嘴［8-10］，而对外混式空气雾化喷嘴工程应用领域的数值模拟研究相对较少。由于雾化理论并不完善，国内外学者更倾向于通过实验方法进行研究，数值模拟方法仍需进一步发展。外混式空气雾化喷嘴通过外部混合装置改变气体压力而不改变液体流率来控制雾化，其雾幅形状为扁平的扇形，有较大的喷雾锥角，使喷嘴可以扫过更大的面积［11］，有利于气相和液相的充分混合，达到较好的雾化效果。鉴于此，有必要对外混式空气雾化喷嘴进行研究，其不仅具有重要理论意义，还有较强现实意义。本文采用计算机模拟与实验验证相结合的方法，分析进气压力对外混式空气雾化喷嘴喷雾锥角和液滴粒径的影响，以及不同混合段的液滴粒径变化规律，验证了数值模拟方法对空气雾化喷嘴进行研究的可行性，可为该类型喷嘴的研究与工程应用提供一定参考。

1 数值模拟

1.1 喷嘴几何模型

本文研究的外混式空气雾化喷嘴结构如图1 所示。压缩空气经空气流道从喷嘴喷出，与液体流道流出的液体在喷嘴附近处混合，通过高速气流与液体间的相互作用完成雾化过程。

1.2 计算模型

粒子轨迹方程：

式中，u和up为气体和液滴速度，ρ和ρp为气体和液滴密度，FD(u-up)为液滴的单位质量曳力。

对于湍流模型，本文选择Realizable k-ε模型，该模型适合的流动类型比较广泛，包括有旋均匀剪切流、自由流（射流和混合层）、腔道流动和边界层流动［12］。对以上流动过程模拟结果都比标准k-ε 模型的结果好，特别是Realizable k-ε 模型对圆口射流和平板射流模拟中，能给出较好的射流扩张，因而在喷雾的模拟计算中被广泛应用。

Fig.1 Structure of air-blast atomizer图1 空气雾化喷嘴结构

关于k 和ε的运输方程如下：

破碎模型选择WAVE 模型，其在高韦伯数液体圆孔射流的破碎与雾化中适用性较好。

表征粒度的方法有算数平均法、质量平均法、体积平均法、表面积平均法等。使用最为广泛的是索特平均直径（SMD）［13-15］，其物理意义是液滴的面积对体积比值等于全部雾滴样品的面积对体积的比值［16］。计算公式如下：

式中，Di为某一间隔的液滴代表尺寸，单位为微米；Ni为某一时间间隔的液滴代表尺寸数量。

1.3 网格划分与边界条件

1.3.1 网格划分

为了满足该型号空气雾化喷嘴的雾化要求，建立300mm×300mm×250mm 的长方体流体域，如图2 所示，并对喷嘴出口处的网格进行局部加密，共划分1 815 113 个网格，继续增大网格数量后对模拟结果影响较小。

Fig.2 Schematic diagram of fluid domain图2 流体域示意图

1.3.2 边界条件

设置理想气体（密度1.29 kg/m3，黏度1.789e-05kg/m-s）为连续项，液态水（密度998.2kg/m3，黏度1.003e-03kg/m-s，表面张力0.071 9N/m）为离散相。喷嘴气体入口采用压力入口（Pressure-inlet），入口压力分别设置为0.05Mpa、0.1Mpa、0.15Mpa、0.2Mpa、0.25Mpa、0.3Mpa、0.35Mpa、0.4Mpa。正对着喷嘴的流体域壁面设置为压力出口（Pressure-outlet），流体域四周设置为无滑移的壁面［17］。

1.4 计算结果与分析

采用Eulerian-Lagrange 耦合模型对空气雾化喷嘴模型进行求解。在Eulerian 坐标系下，将气体介质设置为连续项进行求解。当连续项收敛时，在Lagrange 坐标系下将液滴设置为离散相对喷雾过程进行求解。

图3 是进气压力分别为0.1Mpa、0.2Mpa、0.3Mpa、0.4Mpa时空气雾化喷嘴中心轴线上的气流速度分布图（彩图扫OSID 码可见，下同）。由于中心雾化孔为环状孔，因此在中心轴线起始位置处没有检测到气流速度存在。可以看出，在距喷嘴口约7.5mm 处开始检测到气流速度，此时的气流仅为中心雾化孔喷出的气流，速度会随着距离的增加而有所衰减。在距离喷嘴口约10mm 处，中心雾化孔喷出的气流与辅助雾化孔、扇面控制孔喷出的气流汇合，气流速度很快达到一个峰值，然后开始慢慢随着距离衰减。随着进气压力增大，喷嘴的中心轴线气流速度也在增大，最大气流速度可接近于音速。由于气流速度较大，在喷嘴口附近会产生一定范围的负压区域，且进气压力越大，负压的大小和负压区域的范围会增大。

图4 展示了喷嘴不同混合段处液滴粒径变化。可以看出，随着距离喷嘴口处的轴向距离增大，液滴的SMD 呈现先减小后增大趋势，这是因为液滴刚从喷嘴喷出时，液滴速度较大且分布较为密集，液滴与液滴之间会相互碰撞而产生二次破碎，使得液滴粒径减小；而随着轴向距离的增大，液滴的速度会随之降低，并且液滴由于自身重力的作用与脉动，此时液滴相互碰撞后会产生聚合现象，使液滴粒径增大。还可以看出，随着进气压力的增大，液滴粒径达到最小值所需要的距离缩短，因为压力增大，出口处气体与液滴之间的相互作用也更加强烈，更容易碰撞产生二次破碎。继续增大进气压力后，变化趋势逐渐减缓，是因为气液的相互作用达到一个平衡稳定状态，索特平均直径逐渐达到接近一个极限值，液滴细化效果不会进一步改善。

Fig.3 Distribution of airspeed in central axis of air-blast atomizer图3 空气雾化喷嘴中心轴线气流速度分布

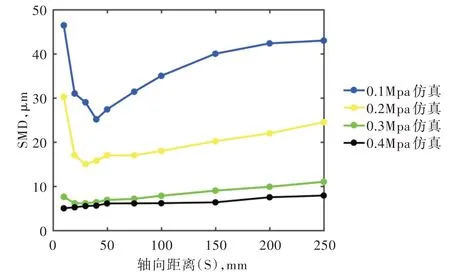
Fig.4 Curves of SMD at different mixing sections图4 不同混合段处液滴SMD 曲线

从图5 中可以看出，当进气压力小于0.2Mpa 时，喷雾锥角随着进气压力的增大呈近似线性增加，与上文对于液滴粒径细化的分析一样，进气压力的增大导致气液相互作用增强，喷嘴的雾化效果越来越好，喷雾锥角也随之增大。

当进气压力大于0.2Mpa 时，随着进气压力的继续增大，喷雾锥角的变化不再那么明显，说明外混式空气雾化喷嘴的喷雾锥角存在极限值。这是因为在外混式空气雾化喷嘴的喷嘴结构中，中心雾化孔和扇面控制孔间存在一个固定夹角（本文喷嘴模型中心雾化孔和两个扇面控制孔间的夹角分别为50°和70°，该夹角会随空气雾化喷嘴型号的不同而有所改变，这种布置可以增强气流与液体之间的相互作用），因此液态水从喷嘴口喷出后的路径主要有轴向和法向两个方向，在进气压力相对较低时，法向方向的空气速度相对较大，液态水会向法向方向扩展，因而喷雾锥角会越来越大。而进气压力增大主要增大轴向方向的空气速度，当压力继续增大时，轴向方向的气流对液态水的影响占主导地位，法向方向的气流对液态水的影响减弱，因而喷雾锥角的变化不再明显。

这点与内混式空气雾化喷嘴有所不同［18］。内混式空气雾化喷嘴的雾化空间有限，随着进气压力增大，气流速度增大，雾化时间缩短，空气与液体未达到充分雾化便从喷嘴喷出，从而导致继续增大进气压力时，雾化效果反而会变差。而外混型空气雾化喷嘴有着充足的雾化空间，因此雾化过程不会受到限制。

Fig.5 Curve of spray cone angle图5 喷雾锥角曲线

2 实验验证

2.1 实验系统搭建

喷雾实验的实验系统由空气雾化装置、供气系统、测量系统和液体回收装置组成。实验分为两部分：第一部分为利用马尔文激光粒度仪对喷雾液滴的SMD 进行测量统计［19］，实验系统如图6 所示；第二部分为利用高速摄影机记录喷雾时的喷雾形态并测量喷雾锥角［20］，该部分实验装置仅在测量装置与液体回收装置上与第一部分实验装置有所不同，实验系统如图7 所示。

Fig.6 System diagram of SMD measurement experiment图6 SMD 测量实验系统

2.2 实验结果及分析

通过调节高压气源的压力调节阀，使气压分别稳定在0.05Mpa、0.1Mpa、0.15Mpa、0.2Mpa、0.25Mpa、0.3Mpa、0.35Mpa、0.4Mpa，因该喷嘴的最佳喷雾距离为170～220mm，用马尔文激光粒度仪测量距离喷嘴出口处200mm处的液滴粒径，并测量从喷嘴口部到最佳喷雾距离范围内不同混合段的液滴粒径，其后用高速摄影机拍摄记录喷嘴处的喷雾状态，并对测得的实验数据进行处理后，得到如下实验结果。

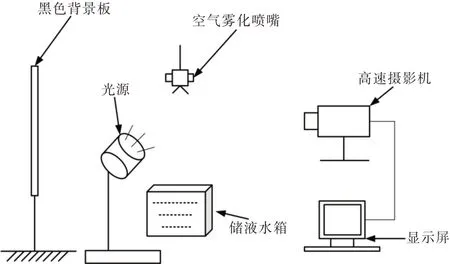
Fig.7 System diagram of spray cone angle measurement experiment图7 喷雾锥角测量实验系统

图8 为马尔文激光粒度仪数据分析软件Data Analysis中得到的不同进气压力条件下喷雾距离为200mm 处的液滴粒径分布图，图9 为不同进气压力下喷雾SMD 曲线图。

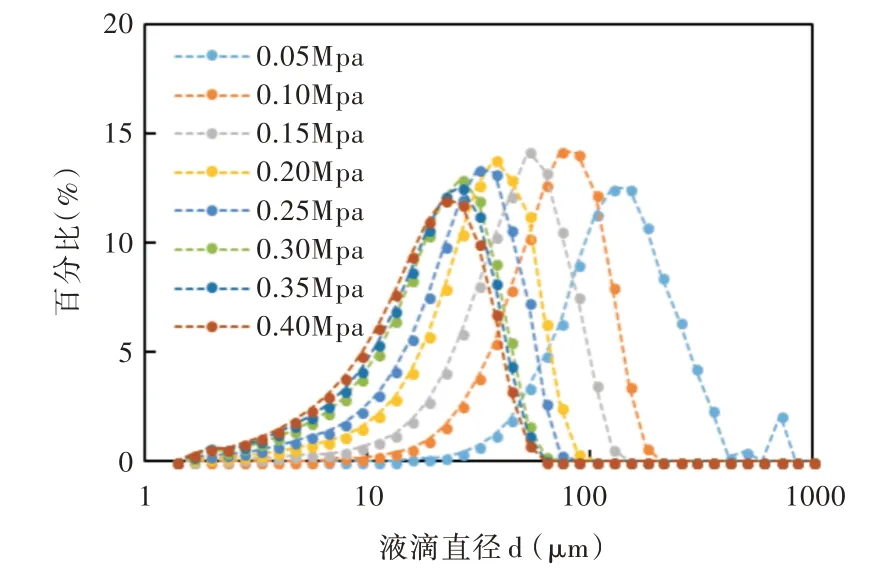
Fig.8 Droplet size distribution at 200mm图8 喷雾距离为200mm 处的液滴粒径分布

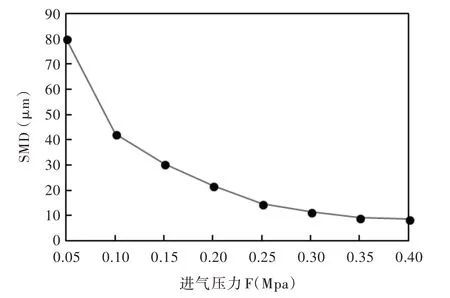
Fig.9 Curve of SMD at 200mm图9 喷雾距离为200mm 处的SMD 曲线

从图8 和图9 可以看出，液滴粒径主要分布在10～100μm 之间，随着进气压力增大，空气与液态水之间的相互作用增强，液滴SMD 减小，继续增大进气压力后，变化趋势逐渐减缓。

通过与高速摄影机配套的图像处理软件，对不同进气压力条件下的喷雾形态图像进行灰度处理与角度测量，得到不同进气压力条件下的喷雾锥角变化曲线，如图10 所示。

Fig.10 Curve of spray cone angle图10 喷雾锥角曲线

通过记录喷涂时间与液体消耗量可以得到空气雾化喷嘴不同进气压力条件下的液体流量，变化曲线如图11 所示。

Fig.11 Curves of liquid flow图11 流量曲线

由于气流速度较大，喷嘴口处附近会产生一定范围的负压，随着进气压力增大，气流速度增大，负压会增大，进出口处压力差增大，使液体流量增大。由于中心喷孔面积一定，流量不可能无限增大。这解释了仿真结果图3 中喷嘴中心轴线的气流速度分布情况。

3 结果对比分析

对不同进气压力条件下的喷雾形态进行角度测量与统计，将得到的数值模拟结果与实验结果进行对比，得到如图12、图13 所示对比图。

Fig.12 Comparison between numerical simulation results and experimental results of spray cone angle图12 喷雾锥角的数值模拟结果与实验结果对比

从图12 中可以看出，喷雾锥角的数值模拟结果与实验结果较为接近，变化规律与实验结果中的分析吻合。由于数值模拟中各项条件均为理想条件，空气为理想气体，且忽略壁面的摩擦阻力，因此得到的雾化效果好于实验得到的雾化效果。

在距离喷嘴不同轴向距离处建立一系列垂直于喷嘴中心轴线的平面，选取该系列平面对喷雾模拟中的液滴进行取样统计，得到不同进气压力条件下不同混合段的液滴索特平均直径，将数值模拟中得到的SMD 值与实验数据中得到的SMD 值进行对比，得到如图13 所示对比结果。

从图13 中可以看出，数值模拟中得到的索特平均直径变化规律与喷雾实验结果中的分析较为吻合，但在压力较低时，空气雾化喷嘴的雾化效果较差，喷雾中存在较大的未破碎液滴，对SMD 的测量会产生较大影响，因而实验结果与理想状态下的数值模拟结果有一定差距。随着压力增大，雾化效果也有较大提升，实验结果与数值模拟结果较为贴近。

4 结语

本文利用马尔文激光粒度仪和高速摄影机，对外混式空气雾化喷嘴在不同进气压力条件下的雾化特性进行了喷雾实验研究，分析进气压力对喷雾锥角和液滴粒径的影响，以及不同混合段的液滴粒径变化规律。采用Eulerian-Lagrange 耦合模型对空气雾化喷嘴进行了数值模拟研究，得出以下几点规律：①进气压力大小对外混式空气雾化喷嘴的雾化效果有较大影响；②随着进气压力增大，空气雾化喷嘴的雾化效果越来越好，喷雾液滴的SMD 逐渐减小，但继续增大进气压力时，液滴细化效果接近极限值，SMD变化幅度不再明显，并且随着喷嘴口处轴向距离的增大，液滴粒径呈先减小后增大趋势，随着进气压力增大，液滴粒径达到最小值的距离减小；③当进气压力小于0.2Mpa、进气压力增大时，气流场的中心轴线速度增大，空气与液体之间的相互作用增强，雾化效果越来越充分，喷雾锥角近乎呈线性增大趋势；当进气压力大于0.2Mpa 时，继续增大进气压力，此时轴向方向的气流速度占主导地位，法向方向的气流影响减弱，喷雾锥角增大不再明显；④随着进气压力增大，液体流量也会逐渐增大，但增大趋势逐渐减缓，由于中心喷孔面积有限，液体流量不可能无限增大；⑤数值模拟结果与喷雾实验结果较为吻合，可以采用数值模拟模型对空气雾化喷嘴的工程应用进行指导。

通过本文研究，有助于研究者对外混式雾化喷嘴雾化特性有更深入的认识。后期可进一步对外混式与内混式雾化喷嘴进行对比研究，探索进气压力不同时，不同混合方式雾化喷嘴喷雾锥角、液滴粒径变化规律的差异性。