多惯性权重的自适应粒子群优化算法
杨博雯,钱伟懿
(渤海大学 数学科学学院,辽宁 锦州121013)
0 引言
粒子群算法(particle swarm optimization,PSO)是由Eberhart和Kennedy于1995年提出的一种群智能优化算法[1].由于PSO算法具有操作简单,参数少,易于实现等特点,因而自从PSO提出后得到了许多学者的认可,并得到迅速地发展.PSO算法中的一个重要参数就是惯性权重,其关键作用能够平衡PSO算法局部搜索和全局搜索能力,从而能够提高PSO的寻优性能,因此许多学者对PSO算法的惯性权重进行了广泛研究.目前关于PSO算法的惯性权重的研究主要集中如下四个方面:(1)常值和随机的惯性权重[2-4],(2)时变惯性权重[5-9],(3)混沌惯性权重[10-11],(4)自适应惯性权重[12-15].虽然不同形式的惯性权重在一定程度上能够提高PSO算法的性能,但是根据“没有免费午餐”定理[16],任何一种带有惯性权重的PSO算法不能对所有问题都有效,本文的思想是:如何合理选用惯性权重使得算法对更多的优化问题有效.本文提出一种多个惯性权重的自适应PSO算法,首先我们定义一个算法K步进化度的概念,选取一些已知的惯性权重构成惯性权重集,从惯性权重集中随机选取一个惯性权重作为当前的惯性权重,当算法进化度不高时更换当前的惯性权重,使得适合解决某一问题的惯性权重能够被多次使用,从而提高算法解决该问题的性能.最后把本文所提出的算法应用到典型的测试问题中,并与其他算法进行比较分析,另外采用了Wilcoxon符号秩检验和Friedman检验两个非参数检验对算法的性能进行了分析.结果表明所提出的算法是有效的.
1 标准PSO算法
在粒子群算法中,每个粒子看作D维空间中的一个点,即表示优化问题的一个解.设t时刻粒子i的位置和速度分别为表示粒子i在t时刻所经历的历史最好位置表示群体在t时刻所经历的历史最好位置.粒子i的位置和速度更新公式为:
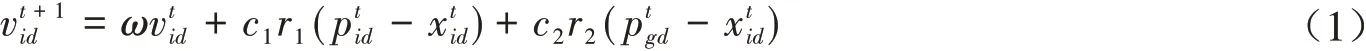

其中ω是惯性权重,c1和c2为加速度因子,r1和r2是[0,1]内的均匀随机数.
2 改进的PSO算法
设惯性权重集W={ω1,ω2,…,ωs},其中每个权重在解决某些问题上具有较好的表现.对某一个当前惯性权重ω∈W,若算法进化较好,我们仍使用当前惯性权重,否则,从集合Wω中随机选取一个惯性权重作为当前的惯性权重,为了评价算法进化的程度,对于极小优化问题,我们定义算法的K步进化度如下:

其中fit(·)表示适应值函数,为了使f it(·)>0,本文取f it(x)=F(x)-a,F(x)为优化问题的目标函数,而a为优化问题允许的最小值.对任意所以由式(3)看出,r(t)∈[0,1),且r(t)越大表明算法进化的越好,r(t)越小表明算法进化的越差,特别当r(t)=0时,全局最优位置没有改善,为此,当r(t)<c(c为阈值)时,更新当前惯性权重,否则保留当前惯性权重.基于上述思想,我们给出多个惯性权重自适应粒子群优化算法,算法过程如下:
1)初始化:设群体规模N,最大迭代步为T,给出加速度因子c1、c2,阈值c及常数K,选择惯性权重集合W={ω1,ω2,…,ωs},随机初始化粒子的初始位置和初始速度
3)从惯性权重集合W={ω1,ω2,…,ωs}中随机选取一个当前惯性权重ω;
4)按式(1)和(2)更新每个粒子的速度和位置;
5)计算每个粒子的适应值,并更新每个粒子的历史最优位置和全局最优位置,得
6)若tmodK=0,则计算算法进化度r(t+1),若r(t+1)<c,则从惯性权重集合Wω中随机选取当前惯性权重ω,否则当前惯性权重不更新;
7)若t>T,则停,否则令t=t+1,转4).
3 数值实验
3.1 测试函数
为了评价本文算法(记为IPSO)的性能,我们从文献[17]中选取13个高维测试函数,具体如下:

表1 单峰测试函数

表2 多峰测试函数
表1中F1~F7为高维单峰函数,表2中F8~F13为高维多峰函数,本文选取的13个函数维数D=30.
3.2 权重集的选取
从常值惯性权重,随机惯性权重,时变惯性权重,混沌惯性权重和自适应惯性权重5个类型中选取12个惯性权重,分别是具有常值惯性权重CONSTANT[2]算法,随机惯性权重RAND[3]算法,时变惯性权重EXP1[6]算法,EXP2[6]算法,LDIW[5]算法和SUGENO[7]算法,混沌惯性权重CHAOTIC[10]算法和RANDCHAOTIC[10]算法,自适应惯性权重AIWPSO[12]算法,DAPSO[13]算法,SSRDIW1[14]算法和SSRDIW2[14]算法.对这12个算法取c1=c2=2,除了算法CONSTANT,RAND,RANDCHAOTIC和SSRDIW2外,取ωmax=0.9,ωmin=0.4,此外,CONSTANT算法取ω=0.7298,所有算法取最大迭代步T=1000,群体规模取N=50,所有算法的程序都是由MATLAB2007实现,且每个实验独立运行30次,平均适应值的实验结果见表3和表4.

表3 AIWPSO,CHAOTIC,CONSTANT,DAPSO,EXP1和EXP2获得的平均目标函数值

表4 LDIW,RAND,RANDCHAOTIC,SSRDIW1,SSRDIW2和SUGENO获得的平均目标函数值

表4续
文[18]提出了用非参数统计检验确定一种群智能优化算法是否优于其他算法的方法.本文用该方法选取求解单峰函数优化问题和多峰函数优化问题的较好算法,我们把12个算法得到的平均适应值与真实最优解误差作为样本,采用Friedman非参数检验方法进行综合比较分析,结果见表5和表6.

表5 单峰函数的Friedman检验结果

表6 多峰函数的Friedman检验结果
从表5和表6可以看出,P-值几乎等于0,表明12种算法在显著水平0.05下求解单峰函数优化问题和多峰函数优化问题存在显著差异.由于本文求极小问题,所以平均秩越小表明算法寻优能力越强.由表5可知,求解单峰函数优化问题较好的前3个算法是:EXP1,AIWPSO,SSRDIW2,由表6可知,求解多峰函数优化问题较好的前3个算法是:CHAOTIC,AIWPSO,SUGENO,因此本文选取AIWPSO,CHAOTIC,EXP1,SSRDIW2,SUGENO五个算法的惯性权重作为本文实验的惯性权重集.
3.3 实验结果比较
本小节把IPSO算法与AIWPSO,CHAOTIC,EXP1,SSRDIW2,SUGENO五个算法进行性能比较分析,并用Wilcoxon符号秩检验方法进行IPSO算法与其他比较算法两两统计分析,用Friedman非参数检验方法进行所有算法综合统计分析.
所有算法的参数设置如下:c1=c2=2,ωmax=0.9,ωmin=0.4,取最大迭代步T=2000,群体规模N=50,IPSO算法中的阈值c=0.1.所有算法的程序都是由MATLAB2007实现,且每个算法对每个测试函数独立运行30次,实验结果见表7和表8.
从表7和表8可以看出,对于“平均目标函数值”来说,IPSO与AIWPSO相比,IPSO在函数F1,F2,F5,F7,F8,F9,F10,F11,F12,F13上比AIWPSO寻优性能好,在函数F6上与AIWPSO性能相同,在函数F3,F4上不如AIWPSO,但是对于“最差目标函数值”来说,IPSO优于AIWPSO;IPSO与CHAOTIC相比,IPSO在函数F1,F2,F3,F4,F5,F7,F10,F11,F13上优于CHAOTIC,在函数F6上与CHAOTIC有相同寻优性能,在函数F8,F9,F12上劣于CHAOTIC,但是对于“最好目标函数值”来说,IPSO在函数F12上优于CHAOTIC;IPSO与EXP1相比,IPSO在函数F2,F5,F8,F9,F10,F11,F13上优于EXP1,在函数F6上与EXP1有相同寻优性能,在函数F1,F3,F4,F7,F12上比EXP1寻优性能差,但是IPSO在函数F1上也能够寻找到较好的最优解,在F7上与EXP1寻优能力几乎相同;IPSO与SSRDIW2相比,IPSO在函数F3,F4,F5,F7,F8,F9,F10,F11,F12,F13上的寻优能力优于SSRDIW2,在函数F6上与SSRDIW2寻优能力相同,在函数F1,F2上劣于SSRDIW2,但是IPSO在函数F1,F2上也能够寻找到较好的最优解;IPSO与SUGENO相比,除了函数F6外,IPSO在其余的12个测试函数上寻优能力都优于SUGENO,在函数F6上与SUGENO有相同的寻优能力.总之,IPSO具有较好的寻优能力,也充分说明IPSO整合5种算法的有效性.

表7 AIWPSO,CHAOTIC,EXP1,SSRDIW2,SUGENO和IPSO对单峰函数实验结果
为了评价IPSO优于其他比较算法的显著性,我们把表7和表8中的平均目标函数值与真实的最优解的误差作为样本,采用Wilcoxon符号秩检验和Friedman检验两个非参数检验方法[18]讨论IPSO的有效性.首先使用Wilcoxon符号秩检验比较两种算法的性能显著差异,在Wilcoxon符号秩检验中,R+表示第一个算法优于第二个算法秩的和,而R-正好相反,用SPSS软件得到的Wilcoxon符号秩检验结果见表9.然后使用Friedman检验所有比较算法的性能显著差异,用SPSS软件得到的Friedman检验结果见表10.
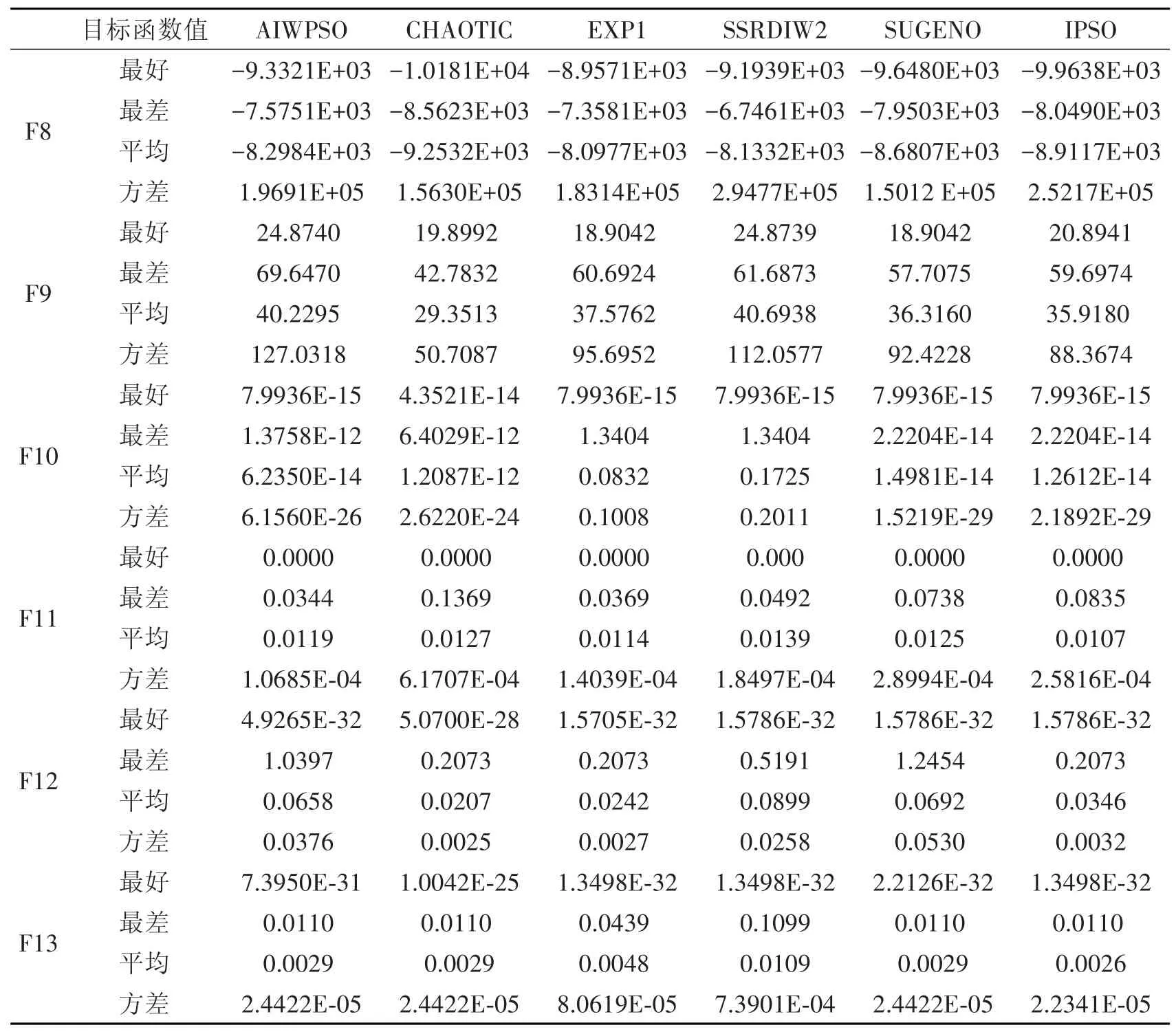
表8 AIWPSO,CHAOTIC,EXP1,SSRDIW2,SUGENO和IPSO对多峰函数实验结果
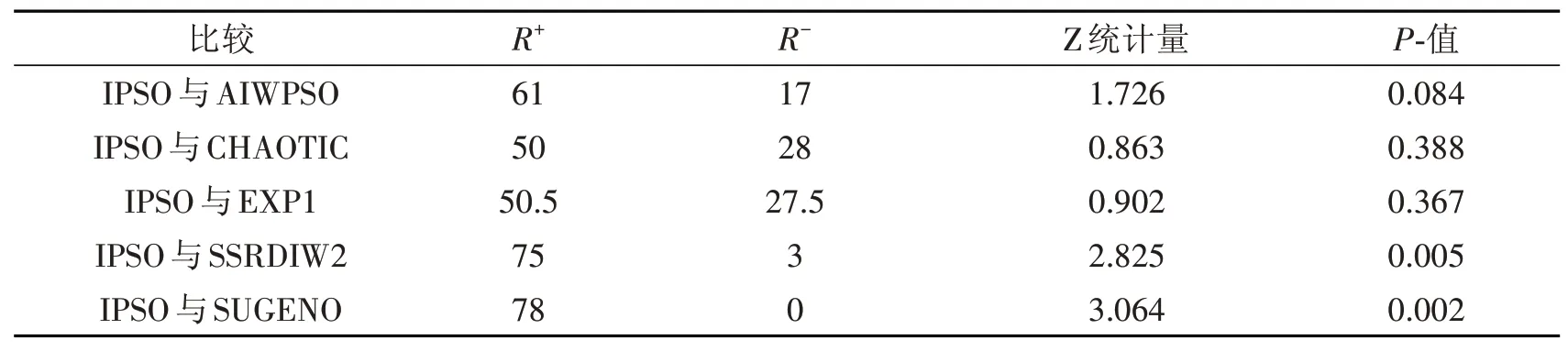
表9 测试函数的Wilcoxon符号秩检验结果

表10 测试函数的Friedman检验结果
从表9看出,基于Wilcoxon符号秩检验,IPSO优于其他比较算法,在显著水平0.05下IPSO显著优于SSRDIW2和SUGENO两种算法,在显著水平0.1下,IPSO显著优于AIWPSO,但是IPSO与CHAOTIC和EXP1没有显著差异.从表10看出,基于Friedman检验,在显著水平0.05下IPSO显著优于其他比较算法.
为了更清楚且直观地比较各种算法的收敛性,我们分别从高维单峰函数和高维多峰函数中各选取三个函数进行收敛曲线分析,图1-图3分别表示测试函数F1,F3和F7的收敛曲线,图4-图6分别表示测试函数F9,F10和F13的收敛曲线.

图1 函数F1的收敛曲线

图2 函数F3的收敛曲线

图3 函数F7的收敛曲线

图4 函数F9的收敛曲线

图5 函数F10的收敛曲线

图6 函数F13的收敛曲线
从图1-图6中可以看出,对于函数F1,SSRDIW2求解精度最好,EXP1与IPSO求解精度相差不大仅次于SSRDIW2,但是SSRDIW2对于函数F9,F10和F13求解精度不好.对于函数F3,AIWPSO求解精度最好,IPSO仅次于AIWPSO和EXP1,但是AIWPSO对于函数F1和F9求解精度较差.对于函数F7,EXP1求解精度较好,IPSO次之,但是EXP1对于函数F10和F13求解精度较差.对于函数F9,CHAOTIC求解精度相对最好,IPSO次之,但是CHAOTIC对于函数F1,F3和F7求解精度不好.对于函数F10和F13,IPSO求解精度最好,优于其他比较算法.总之,虽然某一算法对某一问题解决较好,但是对于其他一些问题解决不好,相对其他比较算法,IPSO对所有问题能够得到最好或较好的结果,这说明IPSO在解决问题时能够利用某些算法的优点,同时克服某些算法的缺点,从而得到比较满意的结果,这正是本文所提出算法的宗旨.
4 结论
本文提出了一种新的自适应粒子群优化算法,其宗旨试图从已知的惯性权重中通过自适应方法选取对求解某一问题较好的惯性权重来解决该问题,以提高所提出的算法能够比较好地解决大多数优化问题的性能.该算法实现简单,推广性较强.为了对该算法进行评价,本文采用两个非参数检验对结果进行验证.实验结果验证了该算法具有优于其他比较算法的显著性能.但是该算法不足之处在于如果惯性权重集中的惯性权重不能解决的问题,该算法也不能解决,所以在未来的工作中,研究新的惯性权重,并与其他求解某问题较好的惯性权重组合方式来实现本文目的.

