求最小树的Kruskal算法中无圈判断的进一步思考
宋慧敏 孙薇 吴建良

【摘要】在实际应用中,我们常碰到实现最小连接的问题,这就归结到最小树问题.最小树问题在运筹学、图论、数据结构等课程都有涉及.解决最小树问题的算法有Kruskal算法和Prim算法等.Kruskal算法的思想是在不构成圈的前提下尽可能选权最小的边.其中考察边和已选的边集是否构成圈是影响算法复杂性的关键一步.本文先介绍实现无圈判断的标号方法,分析其本质需求,进而引入根树方法,并给出进一步改进的思路.本文从运筹学教学的角度阐述教学内容,有意识地引导学生进行深入思考,提升学生进行自主学习的意识和能力.
【关键词】最小树;Kruskal算法;并查集;根树
【基金项目】山东大学(威海)重点教改项目《科研反哺教学的研究与实践》:A201805;山东大学(威海)教研项目《经管类探索性数学实验案例教学研究》:B201816
在实际应用中,我们常碰到实现最小连接的问题,例如交通网、电力网、电话网、管道网等网络设计,这些应用问题简而言之,即如何用最小的成本将一些对象连接起来.若把这些需要连接的对象对应一个个点(称为顶点),若两个对象能够直接建立联系(比如架设电线),则在对应的两点之间连一条线(称为边),两者建立联系的代价(比如架设电线成本)则为对应边的权.这样实际问题就以赋权图(也称网络)的形式展现出来,实际需求也就变成在对应网络里找最小权的连通所有顶点的子图(称为连通支撑子图).最小连接问题可以转化为最小树问题,该问题在大学的许多课程中都有涉及,如运筹学、图论、组合优化、数据结构等.最小树问题在运筹学课程中属于网络优化部分.用网络分析的语言可以如下叙述该问题:给定一个赋权网络,找一个最小权的连通支撑子图.我们知道在所有边权非负的情况下,一定有一个支撑树,达到总权值最小.所以找最小权的连通支撑子图就是找最小权的支撑树(简称最小树),最小连接问题就是最小树问题.从算法复杂性的角度而言,最小树问题是简单问题,有多项式时间算法.现实中很多问题可以转化为网络优化问题,对它们的求解常常要用到最小树算法.最小树算法因其理论和应用价值,教师对其算法进行研究以及对学生进行知识的传授都是非常有意义的工作.
在大部分课程内容中,求解最小树问题都是贪心算法,如Kruskal算法和Prim算法.这些贪心算法能在多项式时间内找到最小树.Kruskal算法的时间复杂度为O(mlog n),Prim算法的时间复杂度为O(n2),其中m表示网络中的边数,n表示网络的顶点数.很显然,在顶点数大、边数相对较小的网络(即稀疏网络)中,Kruskal算法更胜一筹.本文就从运筹学教学的角度,介绍Kruskal算法,重点讲述其无圈判断的实现方法,通过算例演示使学生能较容易地掌握知识内容,又通过目的导向,引导学生深入思考,进而激发学生的研究兴趣.
Kruskal算法是一種贪心算法,其思想很简单,就是在所选边不构成圈的前提下依次选择权值最小的边.设给定网络G=(V,E;W),其中E和V分别是图(即所给网络)的边集和点集,W是定义在边集上的权值函数.令m=|E|,n=|V|,下面算法中,用S存放依次选中的边,|S|≤n-1.算法结束时,若|S|=n-1,则G[S]为最小树;否则,G[S]为最小权支撑森林.
求最小树的Kruskal算法的步骤如下.
第1步,把G中的边按权由小到大排列为a1,a2,…,am,即w(a1)≤w(a2)≤…≤w(am).令i:=0,j:=0,S:=Φ.
第2步,令j:=j+1.若j>m,则该网络不连通,网络的最小树不存在,算法停止;否则,转第3步.
第3步,考察边aj.若G[S∪{aj}]不含圈,则令ei+1:=aj,S:=S∪{ei+1},i:=i+1.若i=n-1,则G[S]即为所求,算法停止;否则,转向第2步.
令T记顶点集为V、边集为S的图,运算进程中,T一直是森林.算法开始,T中无边为空图.顺次考察边a1,a2,...,am,当考察到aj时,若aj与以前选中的边不构成圈,即T+aj仍是森林,则选中aj,开始考察下一条边,接下来T改变,变成T+aj;若aj与以前选中的边构成圈,即T+aj不是森林,则抛弃aj开始考察下一条边,接下来T不变.考察G[S∪{aj}]是否含圈,也就是判断T+aj是不是森林,只需看aj的两个端点是否包含在T的同一个分支.下面我们用一个简单的例子说明该算法.
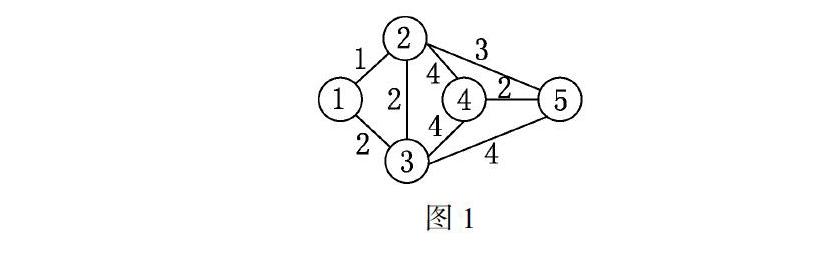
例1 用Kruskal算法求解图1所示网络的最小树,其中每条边上的数表示该边的权值.
解 该图顶点数n=5,边数m=8.按照边权排序为:a1=(1,2),a2=(1,3),a3=(2,3),a4=(4,5),a5=(2,5),a6=(2,4),a7=(3,4),a8=(3,5).
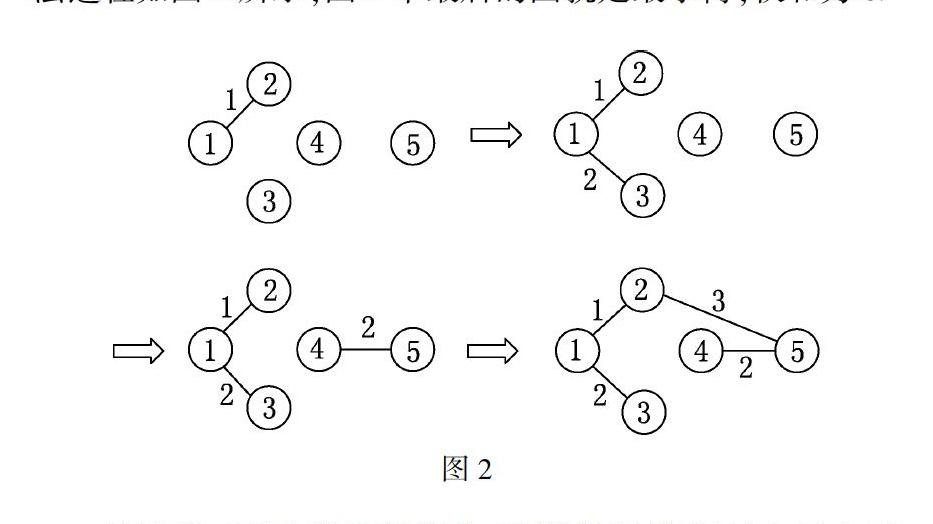
先考虑a1,不构成圈,选中;再考虑a2,与已选中的a1不构成圈,选中;再考虑a3,与已选中的a1,a2构成圈,弃之.再考虑a4,与已选中的a1,a2不构成圈,选中.再考虑a5,与已选中的a1,a2,a4不构成圈,选中.至此,选中的边集为S={a1,a2,a4,a5},选中的边数为|S|=m-1=4,得到最小树.算法过程如图2所示,图2中最后的图就是最小树,权和为8.
从该例可看出算法很简单,手算很容易.但是由于大型网络,用手算不现实,必须用计算机程序实现.如何实现每一步骤,就是编程面临的问题.不同的实现方式导致算法的复杂性不同,网络规模越大,越能显示出效率不同.算法第1步要对m条边根据边权从小到大排序,常用的冒泡排序法的时间复杂度为O(mlog m).第2步没有技术含量.第3步就是我们考虑的重点了.第3步在考察边aj时,要判断G[S∪{aj}]是否含圈,只需检查aj的两个端点是否包含T的同一个分支.换句话说,就是检查aj的两个端点在T中是否连通(即检查连通性).接下来,若选中aj,T改变,aj的两个端点所在的两个分支要合二为一(即合并连通点).
第3步要实现合并连通点(简称“并”)和查询连通性(简称“查”)两个功能.这两个功能对应数据结构课程中的并查集概念.并查集可以高效解决动态连通性.下面就先从标号方法开始介绍,然后是根树方法,最后介绍根树方法的改进思路,由浅入深地介绍并查集的几种实现方式.
标号方法顾名思义是利用顶点标号来实现“并”和“查”两个功能.标号方法需要用一个数组B[1:n]记录每一个顶点的标号,两顶点标号相同当且仅当两顶点在同一分支.初始状态T是空图,每个顶点自成一个分支(或称子树),所以顶点的初始标号可以等于它的编号,即B[i]:=i.当算法第3步考察到aj时,会出现两种情况.情况一,aj两端点标号相同(即两端点在T中连通),则aj不被选择.算法转第2步,考察边计数变量j加1,再轉向算法第3步,即相当于考察下一条边aj+1.情况二,aj两端点的标号不相同(即两端点在T中不连通),则表示aj连接T中不同子树,T+aj自然不含圈,则aj被选中,选中边计数变量i加1,即ei+1=aj.这就完成了“查”的功能.
算法第3步aj被选中后,T改变(置换成T+aj),连通性发生了改变.准确地说,aj的两个端点(不妨设为u,v)在原来T中不连通,分别在两个不同的分支,不妨设u所在分支为Tu,v所在分支为Tv.在T+aj中,Tu和Tv因aj连接为一个分支.标号方法要求同分支顶点标号相同,所以要在下一次“查”操作之前实现“并”功能.很自然的一种想法就是把一个分支的所有顶点标号全换成另一个分支顶点的标号.显然B[u]≠B[v],不妨设B[u]>B[v].搜索Tu,识别Tu中的所有顶点,将它的标号都修改为B[v].这个工作可以通过在原来的图T(边数小于n)中用DFS或BFS找出与u连通的顶点来实现,该步骤的时间复杂度为O(n),至多重复m次.这样整个算法的时间复杂度为O(mlog m)+O(mn)=O(mn).
我们在图3中给出例1的标号过程,图中顶点上的数字为对应顶点的标号.
实现“并”“查”两种功能的方法不同,则会导致算法的时间复杂性不同.上述标号方法的本质是把每一分支的所有顶点都标号为该分支顶点的最小编号.当G连通时,最后所有顶点的标号都为1.如果我们把每一分支的标号等于编号的顶点看成该子树的根,则每个顶点的标号就是其所在子树的根(称为顶点的根)的编号.从这个角度来看,标号方法的“查”操作就是通过比较考察边两端点的根是否相同来实现的,“并”操作也可以看成考察边一个端点所在分支的所有顶点都成了另一个端点的子孙,从而使合并后的分支拥有同一个根.我们还发现,只要这些分支(子树)的顶点集合确定,子树内部的不同连接方式不会影响“并”“查”操作的结果.基于这些思考,我们保证每一分支顶点集合不变,且保持树的特性,将分支对应的顶点集合换一种方式连接,看是否能够降低“并”“查”操作的时间复杂度.根据这个思路将标号算法修改,可得到根树算法.
根树算法是用带根子树族B中的每棵带根子树来对应T=(V,S)中的每个分支,这里B的每棵子树和T=(V,S)对应的分支顶点集合相同,但边集不一定相同.T=(V,S)和B的连通分支有一一对应关系,所以可以用B替代T=(V,S)来实现“并”“查”操作.可以用数组Father[1:n]来记录每个顶点的父亲,一开始可以把每个顶点i的父亲记为i,即Father[i]:=i,也就是每个顶点都是一棵子树,该顶点的根就是它自身.当我们考察aj=(u,v)时,分别找u,v的根ru,rv,这项工作可以通过在B中往上顺序追寻节点的父亲得到.若令h(r)为B中根为r的子树中r到其子孙的最长路长,则该步骤的时间复杂度分别为O(h(ru)),O(h(rv)).若ru=rv,则表示u,v在T的同一个分支,aj不被选择.若ru≠rv,则表示u,v不在同一个分支,则选择aj.这样完成了“查”的功能.若h(ru)≤h(rv),令Father(ru):=rv.文献[2]中用数学归纳法证明了根为r的子树中至少含有2h(r)个顶点,所以h(r)≤log n.任一r的子孙找到r只需h(r)步,这样用根树算法处理Kruskal算法的第3步需要的时间复杂度是O(mlog n),所以Kruskal算法的时间复杂度就是O(mlog m)+O(mlog n)=O(mlog n).
图4给出例1对应的根树序列,每个分支里只作为出发点的节点是对应根树的根,可以看出根树和对应子树连接方式不同.拿最后一次迭代中支撑树和根树进行比较,支撑树中的最大路长是4,而对应根树的最大有向路长是2,所以根树方法比标号方法在搜索方面更快捷.
从上面的分析可以看出,根树方法的时间复杂度取决于树的高度.要想降低时间复杂度,就要想办法压缩树高.改变根树连接方式,压缩树高的方法是不唯一的.下面我们给出其中的几种尝试方向.在算法第3步考查aj=(u,v)时,我们要找u,v的根ru,rv,也就是分别在u,v所在的根树里向上追溯祖先.一种方法,在搜索过程中分别记录(u,ru)-路和(v,rv)-路的中间节点,令它们的父亲都为它们对应的根节点.这样操作有很大可能使根树的树高不超过2,是压缩树高的一种有效方式.在找到根节点之前,路上的中间节点都需要存储,而存储空间变大,是会增加空间复杂度的.空间复杂度是对算法评价的另一个指标,这在实际算法设计和编程中也是需要考虑的一种因素.另一种方法,在寻根过程中每遍历到一个节点,就把该节点变成它爷爷节点的孩子,也就是和它的父节点在一层了.这样通过频繁的查询会导致树的“扁平化”程度更彻底.用这种方式压缩树高没有上一种方式力度那么大,但优点在于存储空间可以有效利用.通过这些大小树合并和树压缩的技巧,“并”“查”两种操作的时间复杂性会非常趋近O(1).这样,Kruskal算法第3步的时间复杂性几乎是线性的.
在数据结构等课程教学中也常涉及最小树的算法实现,其中也有利用Fibonacci堆的处理方法,这里就不一一介绍了.作为教师,我们应意识到即使课程中的简单问题也有值得深入挖掘之处,对教学的投入能够促进科研方面的发展.深入研究教学资料,充分备课,在教学过程中有意识地引导学生深入思考,能够提升学生自主学习的意识和能力.作为高校教师,要教学科研两不误,努力为国家培养高素质创新型人才.
【参考文献】
[1]刁在筠,刘桂真,戎晓霞,等.运筹学:第四版[M].北京:高等教育出版社,2016.
[2] Bernhard Korte,Jens Vygen.Combinatorial Optimization: Theory and Algorithms:Fifth Edition[M].Springer,2011.
[3]Tarjan R E,Data Structures and Network Algorithms[J].SIAM,Philadelphia,1983.
[4]Tarjan R E,Effificiency of a good but not linear set union algorithm[J].Journal of the ACM,1975(22):215-225.

