Testing bubbles based on modified PWY method

Ye Wuyi, Liu Weibo

Department of statistics and Finance，School of management， University of Science and Technology of China, Hefei 230026, China

Abstract: In recent years, the identification and inspection of bubbles has appeared as an important research topic in the financial field. ADF testing method and the PWY alternative method are commonly used, with serial correlation in high-frequency financial time series. In order to remove the influence of serial correlation and be able to test the situation of multiple bubbles at the same sample period, we have made a correction to the PWY alternative method with serial correlation. The BSADF method is used to obtain the statistical sequence, and the corresponding modified critical value sequence is given based on the simulation one. According to the Shanghai Stock Index from 2000 to 2019, an empirical study was conducted based on the GSADF and the revised PWY method to identify and test the bubble phenomenon. The empirical results show that three bubbles appeared between 2000 and 2019, which is in line with the actual financial market conditions, and the traditional PWY method cannot detect all bubbles. Therefore, the GSADF and the modified PWY method given in this article can find bubbles in time and provide some guidance to identify market risks and prevent financial crises.

Keywords: GSADF method；BSADF method；Modified critical value sequence；Examination and detection of bubbles

1 Introduction

The British South Sea Bubble that took place inthe eighteenth century has become the source of the bubble economy. In the past, from the Tulip Fever in Holland in the seventeenth century and the Genroku Bubble Economy in the Edo period to the Real Estate Bubble in the nineteenth century and the Subprime Crisis triggered by the U.S./America in 2007, the burst of each bubble has brought about a financial crisis. Historically, the emergence of financial crises was usually accompanied by asset price bubbles and credit growth. The financial crisis has caused serious blow to the economy of one's own country or even many other countries throughout the world. As a consequence, the research on the identification and inspection of economic bubbles has always been a topic of chief concern among economists and institutional regulators all over the world.

The study of bubbles can be divided into two parts: the first is to detect whether there is a bubble or not; and the second is to get to know when the bubble takes place. The test on the bubble in econometrics is divided into direct and indirect methods. The indirect method considers that the important step in the bubble test is to estimate the size of the bubble. For instance, Mao and Zhou[1]put forward the extended F-O model, and introduce the dividend tax and corporate tax into the original F-O model; Pan[2]improves the dividend discount model, and divide the dividend growth into several stages with different growth rates. However, the academic circle has much dispute over indirect methods. Most scholars believe that although indirect method can directly reflect the severity of bubbles, it cannot separate the bubbles from asset prices. Therefore, most scholars agree with the direct method of testing bubbles, which can study the bubbles straightly through the fluctuations of the share prices. The direct method of bubble research can be divided into two stages. The first stage usually assumes that the bubble is doing the linear motion, for instance, Ferguson[3]believes that when the bubble exists in the asset price, the asset price will rise first and then suddenly fall; Shiller[4]puts forward the variance bounds test method of bubble; Engle and Granger[5]propose a bubble recognition method based on cointegration test. The second stage starts with Norden and Schaller[6], who propose homogeneous Markov domain method to study the relationship between index excessive returns and relative bubble degree, and empirically prove the cyclical movement characteristics of bubbles. Since then, scholars have mostly adopted nonlinear methods for the bubble research, for instance, Ahmed[7]adopts threshold autoregressive method to test the bubble situation in the Asia Pacific region. Zheng[8]utilizes TAR (threshold autoregressive model)model to investigate the time varying characteristics of China's stock market risk premium, and Cui and Liu[9]use the improved TAR model to make an empirical study of the bubbles in Shanghai Stock Market of China.

Historical data show that since the seventeenth century, 60 large and small scale financial crisis events have taken place in the world. Therefore, if the selected sample is large enough , there may be multiple asset price bubblesat the sample period. The recognition of multiple bubbles is often more difficult than the identification of the single bubble, and the calculation of critical values is more complicated when the sample size is relatively larger. Meanwhile, after the occurrence of the Subprime Crisis in 2007, although Chinese scholars’ study on the test method of nonlinear bubbles in the domestic stock market has stagnated to some extent, new research findings on the bubble test have been made among foreign scholars. Phillis et al[10]propose PWY(Phillis ,Wu, Yu) bubble test method, which uses the BADF(Backward Augmented Dickey-Fuller test)method to obtain statistic sequence, Monte-Carlo simulation to get the critical value sequence, and judges the timing of the bubble bursting and generation through the comparison of the statistics and the critical value. Homm and Breitung[11]arrive at the conclusion through simulation that the PWY method has the strongest bubble recognition ability in a series of bubble testing methods. Phillis[12]also proposes that GSADF(Gauss Augmented Dickey-Fuller) can significantly improve the bubble recognition ability, and conducts the empirical study of the monthly index of S&P 500. Since high frequency financial data often have sequence autocorrelation, some improvements have been made specific to the sequence autocorrelation of Phillis's GSADF and PWY methods[12]in this study for the bubble research model more applicable to high frequency data (Shanghai Index): ①as for the ADF method, in order to eliminate the correlation between the Shanghai Composite Index's weekly data, the lag orderkin the regression equation needs to be adjusted, the BG(Breusch-Goldfrey)test for autoregressive residuals at differentkvalues needs to be conducted to find out the appropriatekvalues to eliminate the autocorrelation, and finally the appropriatekvalues are selected as the parameters of our model; ②in the traditional PWY method, it is found that the statistics calculated by the BADF method cannot accurately detect the bubbles after the occurrence of the first bubble when there are more than two bubbles in one cycle. As a result, the BSADF method is usedto obtain the sequence of statistics. However, the calculation process of the critical value sequence obtained by the Monte-Carlo simulation is complex and time-consuming. Therefore, a simpler method is proposed to estimate the critical value sequence. Finally, in order to verify the validity of the new revised method proposed in this paper, the improved model is applied to conduct the empirical test of the Shanghai Composite Index from 2000 to 2019, which is compared with the traditional bubble test method.

2 Model and method

2.1 Asset pricing formula

Before studying the financial bubble, the asset pricing formula of assets proposed by reference[10]needs to be comprehended in the first place.

(1)

Among them,Ptis the asset price after the payment of the interest;Dtis a dividend;rfis a risk-free interest rate;Utis the fundamental hard to be observed;Btis the bubble, andBtsatisfies the following

Et(Bt+1)=(1+rf)Bt

(2)

When there is a lack of bubbles in the market, the stability of asset prices is controlled by dividends and unobserved fundamentals. For instance, ifDtis a first-order difference process, andUtis a first-order difference process or a zero order difference process, thenPtis at most a first-order difference process. Therefore, when the difference ofDtandUtis stable, the phenomenon of instability in asset prices can be used to deduce the existence of the bubble.

2.2 ADF test method and GSADF method

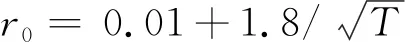
(3)

In order to detect the existence of bubbles more accurately, Phillips also proposes the GSADF method based on the ADF method. In the ADF method, the starting point and ending point of the sub-sample are fixed. For the GSADF method, the ending pointr2changes in [r0,1] and the starting pointr1changes in [0,r2-r0] . In this bidirectional recursive cycle, the GSADF statistic is the maximum value in the sequence of the ADF statistic, and is marked as GSADF (r0) :

(4)

For the GSADF statistic, its asymptotic distribution is

(5)

rw=r2-r1.Wis a standard Wiener process.

The GSADF method is a one-tailed test.H0: for allr2∈[r0,1] andr1∈[0,r2-r0] . there is an autoregressive coefficientβr1,r2=0 . that is, no bubbles exist in the whole time series.H1: for allr2∈[r0,1] andr1∈[0,r2-r0] . there is at least one set of (r1,r2), which can make autoregressive coefficientβr1,r2>0, that is, bubbles exist throughout the time series. As a consequence, if the null hypothesis is rejected, it is believed that there exists a bubble in the sequence.

2.3 PWY method

The analysis of bubbles cannot only be limited to the detection of the existence of the bubbles since it is more significant to the identification of the timing of bubble occurrence and burst. The PWY method provides a precise way to estimate the timing of bubble occurrence and burst. The PWY method is the one based on the BADF test. BADF can be regarded as a special way of GSADF. In BADF, ifr1=0 ,r2∈[r0,1] . the BADF statistic of the corresponding sub-sample is obtained, which is recorded as follows

(6)

(7)

(8)

If there is a bubble in the sequence, it must be ensured that its duration exceedsδlog(T) . so as to eliminate the effects of short term market fluctuations. Generally, 0.7 is taken for monthly dataδand 5 is taken for weekly dataδ.

The PWY method can be asymptotically used and estimate the occurrence and burst timing of the first bubble with one accord.

(9)

When formula(9)is satisfied，we have

2.4 Amendment of lag order K

By observing formula (3), it can be found that the selection ofKvalue has some influence on the calculation of the ADF statistics. In reference[1], the monthly data of the U.S. Stock Market are used for study, andkvalue is 0. In this paper, the weekly data of the Shanghai Composite Index in China are selected for study. Ifk=0 is still selected, the OLS method will invalidate and the ADF statistics calculated will be biased. Therefore, it is necessary to reset the value ofKto ensure the consistent estimation of regression coefficient in OLS.

Firstly, differentKvalues are selected to calculate GSADF values, and whether differentKvalues will affect the results is tested. Then, a group of asset price data are simulated for the simulation experiment. The simulated asset price sequence is based on the Lucas asset pricing model and the Evans[13]Bubble Burst Model

(10)

(11)

As for bubbles:

Bt+1=ρ-1BtεB,t+1，ifBt

(12)

Bt+1=[ζ+(πρ)-1θt+1(Bt-ρζ)]εB,t+1，ifBt≥b

(13)

After generating 500 data,k=0,k=1,k=2,k=3,k=4, are set respectively to calculate GSADF of the sequence based on the AIC criteria. The results are in the table below:

From Table 1, it can be seen that the GSADF value obtained increases with therise of theKvalue. Therefore, it can be obtained that the setting of theKvalue has a great impact on the research. If theKvalue is too small, the GSADF acquired will be smaller and easier to be subject to the bubble free null hypothesis, resulting in detection errors.

Table 1. GSADF values under different k values.

Table 2. BG statistics and residuals under different k values.

From the above simulation results, it can be seen that the selection of theKvalue will affect the results of bubble detection. Therefore, the appropriateKvalue will be selected according to the specific rules in the later empirical study. The selection of theKvalue is to eliminate the autocorrelation between data. Whether there is autocorrelation can be detected by conducting the BG test on the autoregressive residuals.

Firstly, a group of third-order autocorrelation data are generated according to the above rules, and the sample size is 500. Thenk=0,k=1,k=2,k=3,k=4,k=5 are selected to calculate BG statistics andPvalues of autoregressive residuals. The results are as follows:

From Table 2, it can be found that when thepvalue is greater than 0.05 and tends to be stable whenk=4.which means that the autocorrelation can be basically eliminated afterk=4. and is also consistent with the setting that our simulation data is third-order autocorrelation. As a consequence, the BG test on autoregressive residuals can effectively detect whether there is autocorrelation between the data. As high frequency data (weekly data of the Shanghai Stock Index) are selected in this empirical study, the BG test should also be used to select the appropriateKvalue for the elimination of the autocorrelation between data.

Table 3. GSADF value under different r0.

2.5 The influence of the minimum window width

According to Table 3 , it can be found that whenr0is selected less than 0.1, the GSADF value does not change much. However, the increase in the number of subsamples will lead to more complicated calculation process. Whenr0is selected more than 0.1, the GSADF value will decrease significantly; and when ther0value is selected to be 0.2, the GSADF value will be less than 2.65 ，which is the 95% of the confidence level. As a consequence, the null hypothesis of having no bubbles will be more acceptable in the actual forecast. To sum up, it is reasonable to have ther0selected according to the criteria, which can ensure the accuracy of the results without increasing the complexity of calculation. Therefore,r0can still be determined according to this criterion in the empirical study of the paper.

Table 4. The actual value and estimated value of bubble generation and burst time.

2.6 Revised PWY method

The traditional PWY method can be divided into two parts: One is to obtain the statistics of sub-samples based on the continuous initialization of the BADF method; the other is the generation of the critical value, which is obtained by the Monte-Carlo simulation of each subsample. Therefore, this paper will also revise the PWY method in these two aspects.

First of all, the BADF method is taken into account. The BADF method can accurately and uniformly estimate the first generation of the bubble burst time on the condition that the asymptotic consistency is satisfied. Then, is it possible to estimate the subsequent bubble accurately? This paper selects the Shanghai Stock Exchange Index from December 1990 to December 1996 (before the implementation of the Raising Limit System), and analyzes the weekly data of the Shanghai Stock Exchange In Figures 1 and 2, it can be seen that the Shanghai Stock Index is not stable. It is calculated that the GSADF of this period is 5.913, which is greater than 95% of the GSADF value of 2.80, indicating that there is a bubble in the Shanghai Stock Index during this period.

By observing Figures 1 and 2, it can also be found that there is a large fluctuation in the Shanghai Composite Index between 0～100. Therefore, it is estimated that there exists a bubble period between 0～100. In order to verify whether there is a bubble following up, the sequence is divided into two segments: the first is from 0 to 100, and the second from 101 to 305.

Figures 1.The weekly data of the Shanghai Stock Exchange Index from 1990 to 1996.

The blue curve is the BADF sequence and the black curve is 95% of the critical value sequence.

The sequence is divided into two segments: the first segment is from 0 to 100 and the second is 101 to 305. The calculated GSADF values of the two segments are 5.913 and 2.88, which are also larger than the GSADF values below 95%, thus it comes to the conclusion that there are at least two bubble periods. The BADF method is used to test the bubble. The minimum sample size is 40. The BADF statistics series and the critical value sequence diagram are as follows:

From Figures 1 and 2, it can be seen that there is a bubble in the period of 0～50, but after 50, the sequence values are less than the critical values, indicating that there are no bubbles in the sequence after 50, which is not consistent with the conclusion that at least two bubbles exist. Therefore, when there are multiple bubbles in the sequence, the BADF method in the traditional PWY method cannot accurately detect the subsequent bubble after the first bubble in some cases.

The blue curve is the BSADF sequence and the black curve is 95% of the critical value sequence.

Figures 4. The simulated data.

According to reference[12] it can be learnt that when there are two bubbles in the sequence and satisfy formula (5), the traditional PWY method can consistently estimate the timing of the occurrence and burst of the first bubble. As for the second bubble, if the duration is less than the first one, it is impossible to detect the existence of the second ; if the duration is not less than the first bubble, the second can be detected. However, the timing of the occurrence and burst of the second bubble cannot be accurately estimated.

In view of the above phenomena, this paper will use the BSADF method proposed by Phillips[12]to replace the BADF method. In the BADF method,r1will be fixed at 0, and then the sequence statistics will be obtained by runningr2fromr0to 1. In the BSADF method, for eachr2.r1will run from 0 tor2-r0. and the maximum value is taken in the whole subsequence, that is

(14)

The BSADF statistics sequence and critical value sequence of the sequence can be obtained by using the above BSADF method, as shown in Figures 3 and 4.

Figures 5. The weekly data of the Shanghai Stock Index from 2000 to 2019.

The blue curve is revised critical value and black curve is the BSADF statistics.

The blue curve is revised critical value and black line is BADF statistics

As can be seen from the above chart, the existence of subsequent multiple bubbles can be detected after the application of the BSADF method, which is also consistent with the fact that bubbles occur frequently before the implementation of the Raising Limit System in China. And from the above chart, it can be found that the duration of the second bubble is indeed shorter than the first one, which is consistent with our conclusion that BADF cannot detect a continuous one.

Secondly, the critical value correction is taken into consideration. The calculation of the critical value in the traditional PWY method is obtained by the Monte-Carlo simulation. However, for the test of multiple bubbles, the Monte-Carlo simulation is needed for each sub-sample, the process of which is complex and time-consuming. If the critical value of asymptotic distribution is applied, the premise is that the sample must be the large-scale sample, but the minimum sample in the BSADF method is [Tr0], which may not meet the needs of large samples. Therefore, this paper attempts a more convenient critical value proposed by Wu[10]: ln(ln(t))/100.tis the size of the sub-sample. In comparison with the Monte-Carlo simulation, this method is simpler to calculate the critical value, and the requirement of the large-scale sample size is omitted by comparing the asymptotic distribution. The following is to test whether the new critical value satisfies formula (9),cvβT=ln(ln(t))/100 .tcan be regarded asTmultiplied by a coefficientrof 0～1, andt=Tr. WhenTtends to infinity,ttends to be infinite.

(15)

(16)

Meanwhile, it can be arrived at by applyingL' Hospital's rule

Therefore, the new critical value satisfies formula (5). At the same time, when the size of the sub-sample increases from 40 to 1000, the new critical value increases from 0.013 to 0.017, and the growth is slow and does not exceed 99%of the asymptotic critical value.

It is tested in the following part whether the PWY method that applies the new critical value to the simulated data is asymptotically consistent or not. The simulation data are generated in the first place. The simulation process is the same as that in (four) simulation methods with 500 simulated data, which are shown in Figure 4.

By observing Figure 4, it can be seen that there are three peaks in the range of 75～79, 146～159, and 324～334. Since the first-time occurrence is too short, it is excluded. Therefore, it is believed that there are two bubble events in the simulated sequence, and the birth and death time are 146～159 and 324～334.

Then the revised PWY method (cycle BSADF and new critical value sequence) is used to study the generation and burst time of the bubble. The results are as follows.

According to the above table, it is known that the timing of bubble generation is closer to the actual value, and the timing of bubble burst is the same as the actual value. Therefore, the revised PWY method can accurately estimate the time of the generation and burst of bubble. In the meantime, when the critical value of the simulation data is calculated, the computing times of the two sets of critical value sequence are respectively calculated and obtained. WhenT=500, the critical value obtained by the traditional critical value sequence through 2000 Monte-Carlo simulation takes about 200 minutes, while the new critical value sequence only takes about 1 second.

Therefore, we know that the new critical value sequence still satisfies the asymptotic consistent condition, and can accurately estimate the time of the formation and collapse of the bubble, and it is more convenient than the traditional critical value calculation.

3 Empirical analysis

3.1 Data description

The data selected in this paper are the weekly data of the Shanghai Stock Index from January 4, 2000 to December 31, 2019, counting up to 960 data. First, the weekly data of the Shanghai Stock Index from 2000 to 2019 are drawn to form a chart as Figure 5.

From the Figure 5, it can be observed that during the period from 2000 to 2019, the Shanghai Stock Index have experienced several large fluctuations: ①the stock price begins to grow rapidly at the beginning of 2007, and increases by more than 250% in only 10 months, leading to the over exceeding of the stock price beyond the real value, which is in line with the actual situation of overheated investment in 2007. In October 2017, the stock price begins to plummet. The slump is caused by the outbreak of the U.S. Subprime Mortgage Crisis in August. ②The stock price grows rapidly in September 2014, reaching its peak at the end of May of 2015, and increases by more than 200% in eight months. The sharp fluctuation of the stock price is related to the frequent reduction of interest rates by the central bank in the fourth quarter of 2014 and the first half of 2015. The down-regulation of the interest rates causes investors to enter the market in a row, causing the share price to deviate rapidly from the real value.The bubble level further aggravates, and finally slumps in June. ③During the first half of 2018, the share price begins to increase modestly in the first half of 2018 pertaining to the listing of many new shares, begins to decline in May of 2018, and then continues to decline within half a year. This decline is caused by the failure of Sino-U.S. negotiation in May 2018, which leads to the loss of confidence of investors in the stock market, and the stock price slumps in the second half of the year.

Through the analysis of the data from 2000 to 2019, it can be learnt that there exist bubbles, and the number is more than one during this period. In the following part, the GSADF method with the parameters adjusted and the revised PWY method are used to conduct the empirical test.

3.2 Empirical test of bubble

First, the lag order k is selected which can eliminate the autocorrelation between empirical data. For the weekly data of Shanghai Stock Index from 2000 to 2019,k=0,k=1,k=2,k=3,k=4,k=5 are respectively set to calculate the BG statistics and thePvalue of autoregressive residuals shown in Table 5.

From Table 5, it can be found that the value ofPtends to be stable afterk=3, thus the conclusion can be arrived at that the autocorrelation between empirical data can be eliminated by selectingk=3 and subsequent values. In order to simplify the calculation and eliminate the correlation between the data,k=3 is set in the empirical study.

Next, whether there exist bubbles is tested. First, Monte-Carlo simulation is used to get the right critical value of GSADF asymptotic distribution shown in Table 6.

Table 5. BG statistics and residuals under different k values.

Table 6. Critical values under different confidence levels.

Table 7. GSADF under different k values.

k=0 andk=3 are respectively selected for the calculation of the GSADF of the weekly data of the Shanghai Stock Index from 2000 to 2019, and the results are According to the table, whenk=3 andk=0 . the results are 4.58 and 2.13 respectively. Whenk=3 . the GSADF value is 4.58, which is greater than the critical value of 3.42 at the 99% confidence level. Therefore, the original hypothesis without bubbles can be rejected, which indicates that there exist bubbles in the Shanghai Stock Index during this period, and is also consistent with our analysis of the 2000～2019 annual inspection data. Whenk=3 . the GSADF value is 2.13, which is smaller than the critical value of 2.13 at the 90% confidence level. The acceptance of the original hypothesis without bubbles is obviously inconsistent with the actual situation, which also shows that the parameter setting ofk=0 in the original model is not consistent with the weekly data of China's stock market, and the new parameters set are in line with the actual situation.

Being informed of the existence of the bubbles in the cycle, there is a must to ensure that there are at least two bubbles in the cycle to enable our model to test the multiple bubbles in the cycle. In the data analysis, several violent fluctuations of the Shanghai Stock Index from 2000 to 2019 are simply analyzed. Therefore, 2010 is taken as the dividing point to calculate the GSADF of 2000～2010 and 2010～2019 respectively. The GSADF of 2000～2010 is 4.58, and the GSADF of 2010～2019 is 3.69, both of which are greater than the critical value of 3.42 at the confidence level of 99%, thus there exist at least two bubbles at our chosen sample period.

Finally, timings of the bubble occurrence and burst will be distinguished. The BSADF sequence value and the modified critical value sequence during this period are respectively calculated, as shown in Figures 6 and 7.

The BSADF statistics and the revised critical value during this period are calculated.

Through the comparison between Figures 6 and 7, it can be found that in the application of the revised PWY method, it is detected that the BSADF statistics in the cycle exceed the critical value many times, that is, there are multiple bubbles, which is also consistent with our aforementioned arguments. When applying the traditional PWY method, it is found that BADF statistics only exceed the critical value sequence at one time, that is, there is only one bubble in the cycle, which is not in line with our conclusion above. The first bubble detected by applying the BADF and BSADF methods in the 2007～2008 year shows that the traditional PWY method can accurately estimate the time of occurrence and burst of the first bubble in the cycle of multiple ones, but cannot accurately detect the bubble condition after the first one, while the revised PWY method can accurately and consistently estimate the time of occurrence and burst of each. At the same time, it can be found that the duration of the second bubble in the cycle is obviously shorter than that of the first, which also confirms our previous conclusion that when the second bubble duration is shorter than that of the first, the traditional PWY method cannot detect the second bubble. The comparison results show that the revised PWY method is effective in detecting multiple bubbles in the cycle.

The blue curve is revised critical value and black curve is BSADF statistics.

In the next, Figure 6 will be analyzed. According to Figure 6, it can also be found that the value of the BSADF sequence exceeds the critical value five times. However, in order to eliminate the impact of the short term fluctuations on the market economy, the bubble is regarded to occur when the BSADF value exceeds the critical value time byδlog(T). For the weekly data,δtakes 5 andTtakes 983. Therefore, it is believed that the bubble occurs only when the duration exceeds 14. Therefore, it can be learnt from the Figure 2 that there are three bubbles in this period: the first is 2007.1.10～2008.4.15, the second is 2014.9.5～2015.5.26, and the third is 2018.3.30～2018.6.25. The three bubbles will be analyzed in the following part.

The first bubble: on January 10, 2007,the BSADF statistic exceeded the critical value, and then began to grow rapidly, indicating that the bubble rapidly expanded and the speed became faster and faster after the occurrence of the bubble. In November 2007, the statistics reached its peak, then began to decline, indicating that the rate of inflation began to slow down from October 2017, and finally decreased below the critical value in April 2008, that is, the bubble burst at this time. The bubble was mainly caused by the Subprime Crisis in the U.S.A. which broke out in 2007. The U.S. mortgage risk began to become visible on February 13, 2007, and became more and more serious in the following half year, leading to the slump of the U.S. stocks, and the worst situation in the credit market in 20 years. Since August 2007, the Subprime Mortgage Crisis began to spread to the global financial market. China is also affected, and the stock index plummeted in October 2017. This bubble was mainly due to the impact of the international financial environment, which has prompted us to pay close attention to international financial forms and make adjustment to domestic economic policies in time of changes.

The second bubble: the BSADF statistics exceeded the critical value in September 2014, and then began to rise rapidly, reaching the first peak in November 2014. Then the statistics dropped and then rapidly increased in January 2015 to the second peak, then began to decline and fell below the sequence value in May 2015, thus the bubble burst. The bubble was mainly triggered by the change of monetary policy in China. It can be seen that the bubble had two rapid expansion stages, which was related to the central bank's lowering of the repo rate in July 2014 and the lowering of the deposit and loan benchmark interest rate announced by the central bank in November 2014. Since the two lowering first appeared in 2014, many people viewed this as a forthcoming announcement of the bull market, and a large number of investors poured into the market. During the period from May 2014 to May 2015, the central bank also lowered the deposit and loan interest rates several times, resulting in the generation of bubbles and the two times of rapid growth. The Shanghai Stock Index increased more than 200% in the months from May 2014 to May 2015, and finally the bubble burst in June 2015, and the Shanghai Stock Index plummeted in June. This bubble suggests that investors should interpret economic policies correctly and avoid over reactions.The regulators should discover bubbles in time and make policy adjustments.

The third bubble: as shown in Figure 2, the bubble level is much smaller than that of the first two and the duration is very short. The reason for the bubble is due to the large number of new shares listed at the beginning of the year and the stock price being severely overestimated. But in accompaniment of the Sino-U.S. trade war triggered by the failures of three Sino-U.S. trade negotiations in May, and the investors have lost confidence , resulting in the stock market's lack of new capital entry and the burst of the bubble. The stock market continued to fall. At this time, the policy did not release timely bull news to boost or stimulate the stock market to stop falling and get stabilized, but rather allowed it to work on its own, thus triggering a vicious spiral. In 2018, the Shanghai Stock Index fell by 813.27 points, and the range is up to 24.59%.

Through the above analysis,it can be found that the revised model can estimate the birth and death time of each bubble of the Shanghai Stock Index accurately in round Figures. For a more convincing model, the Shenzhen Component Index of the same time period is selected. After calculation, the GSADF value is 3.96，which indicates that there was a bubble in the Shenzhen's index at that time, and then the BSADF sequence and the revised critical value sequence are obtained by using the modified model.

It can be seen from the above Figure that from 2000 to 2019, there were three bubble events in the Shenzhen Component Index, which last from 2007.1.19 to 2018.5.16, from 2014.11.28 to 2015.4.30 and from 2018.4.5 to2018.7.30 respectively, all close/similar to those of the Shanghai Stock Index. Therefore, the model can be used to identify and detect bubbles in a comparatively accurate manner.

4 Conclusion

this paper has modified the parameters in GSADF and setting appropriate parameters, eliminated the correlation between Chinese market weekly data and made two improvements in the calculation of critical values and statistics in the PWY method, thus the new critical value sequence satisfies the requirements of the establishment of the asymptotic consistency as well. The new BSADF statistics can accurately estimate multiple bubbles in the same cycle, which makes an empirical study on the Shanghai Stock Index from 2000 to 2019. The results show that there are three bubbles in China’s stock market from 2000 to 2019. The three bubbles are caused by the U.S. Subprime Mortgage Crisis, the interest rate reduction policy of the Central Bank of China and the Sino-U.S. trade war.

The inspiration from these bubbles is that there are internal and external factors in the occurrence of the bubbles in China. Under the gradual strengthening of international financial market integration, every country is increasingly influenced by the international financial market. The stability of a country's financial market is not only related to the domestic macro environment, but also affected by the world economic environment. Internationally, our country should always pay attention to the international economic forms and take the early warning against the global bubble in time to prevent it from spreading to our market. In China, the effective regulatory bodies and policy-making institutions should be established. When a new round of policies are introduced, the occurrence of bubbles should be strictly guarded against, and early steps should be taken to prevent aggravating bubbles , which will release the energy in the form of the slump of the stock price.