Event-triggered sliding mode load frequency control for multi-area interconnected power systems under deception attacks
Liu Xinghua, Bai Dandan, Sun Baoren, Wen Jiayan, Lv Wenjun, Li Kun
1. School of Electrical Engineering, Xi’an University of Technology, Xi’an 710054, China; 2. Huaneng Chaohu Power Generation Co. LTD, Chaohu 238000, China; 3. School of Electrical and Information Engineering, Guangxi University of Science and Technology, Liuzhou 545616, China; 4. School of Information Science and Technology, University of Science and Technology of China, Hefei 230026, China; 5. Institute of Advanced Technology, University of Science and Technology of China, Hefei 230088, China
Abstract: In this paper, the problem of sliding mode load frequency control (LFC) is probed for the multi-area interconnected power system under deception attacks. In the case of deception attacks, a Luenberger observer is designed to generate state estimation of the multi-area power systems. An event-triggered mechanism is introduced to reduce the frequency of controller updates and communication between nodes. Sufficient conditions are proposed to achieve asymptotical stability by utilizing sliding mode control and Lyapunov-Krasovskii (L-K) functional method. Then the sliding mode controller is synthesized to ensure that the trajectory of the closed-loop system can be driven onto the prescribed sliding surface. Finally, the effectiveness of the design scheme is verified by a three-area interconnected power system.
Keywords: Load frequency control, deception attacks, sliding mode control, event-triggering mechanism
1 Introduction
Small changes in frequency will have serious impact on the interconnected power grid. One reason is that it is difficult to estimate the frequency variation caused by a load, and the second is the area exchange on the tie-line power changes, which will bring challenges to the stability of the frequency[1]. Load frequency control (LFC) is an important means to solve the power grid frequency change caused by load variation. Its main function is to ensure the stability of the load frequency of the multi-area interconnection power systems[2]. Frequency stability is an important index of power quality of the power systems[3]. The target of LFC is mainly realized by adjusting the frequency deviation value of the grid and the exchange power value of the tie-line. However, any sudden change of the load may lead to the deviation frequency, which will then seriously affect the stable operation of the systems. Therefore, to ensure the power quality and system stability, an LFC system is required to adjust the frequency of the systems to the rated value and maintain the exchange power of the regional tie-line as the planned value.
In recent years, with the rapid development of computer network and communication technology, an important type of network control systems (NCS) has been formed. On the one hand, these developments can improve the monitoring efficiency of the power systems and promote information communication. On the other hand, this also leads to the possibility of network attacks on the power systems, and brings challenges to the network security. Hence, it is urgent to analyze the network attacks and study the network security under the network attacks[4-10]. The deception attack is an attack approach in which the attackers impersonate a normal user to gain access to the target or obtain key information, which belongs to such attack techniques as obtaining passwords, malicious codes and the network deception. Deception attacks will affect the stability of power systems operation, and cause systems to breakdown in serious cases. In references[4-6], an advanced resilience event-triggered LFC scheme is proposed, which can reduce the communication burden while resisting DoS attacks in terms of the defense effect and the average trigger period. In references[7-9], , the multi-area LFC power systems under hybrid network attacks, including DoS attacks and deception attacks are studied, and a switching system model with DoS attacks and stochastic deception attacks is established. The stabilization problem of the distributed network control systems under stochastic deception attacks is studied and a decentralized mixed sampling-data strategy is proposed in reference[10] by using the hybrid nondirectional triggering mechanism.
In view of the above network attacks, there exist the robust control[11,12], sliding mode control(SMC)[13-15], fuzzy control[16], static feedback output control[17]and other methods. A robust state observer is designed[12], which can be used as a detection monitor with guaranteed performance. In reference [13], the finite time convergence problem of the sliding mode variable structure control is considered for a class of uncertain multivariable linear systems, where an exponential nonlinear convergent sliding hypersurface is proposed and its corresponding control scheme is provided. Huang et al[14]establish an adaptive integral sliding-mode control for cyber-physical systems against a class of actuator attacks. Tang et al[15]propose a position sliding mode control for DC-motor position tracking based on a high-gain observer. Compared with other control strategies, the sliding mode control can be independent of object parameters and has no need of online system identification, which shows insensitivity to parameter changes and disturbances.
To sum up, this paper studies the LFC problem of the multi-area interconnected power systems under deception attacks. So far, this paper is the first to use the event-triggered sliding mode control to solve such problems. The main contributions of this paper are described below.
(Ⅰ) The event-triggered sliding mode LFC under deception attacks is modeled, which lays a foundation for studying the security of multi-area interconnected power systems.
(Ⅱ) Aiming at the security problem of the multi-area interconnected power systems, the event-triggered sliding mode LFC strategy is proposed in this paper to realize the stable operation of the systems under deception attacks, which can avoid a lot of unnecessary data transmission and effectively save network resources.
(Ⅲ) The simulated results of a three-area interconnected power system in a simulation case show the effectiveness of the proposed strategy.
The rest of this paper is organized as follows. In Section 2, we present the dynamic model of the event-triggered sliding mode LFC under deception attacks. In Section 3, we analyze the stability of the system and carries on the accessibility analysis. A simulation case is used to verify the proposed method in Section 4. Finally, Section 5 concludes this paper.
NotationsThe following notations are used throughout this paper. E{·} represents mathematical expectations. diag{·} represents the diagonal matrix. Let ‖x‖ and ‖A‖ be the Euclidean norm of a vectorxand a matrixA, respectively. For a symmetric block matrix, we use * to denote the terms introduced by symmetry. We use Rnto denote then-dimensional Euclidean space. sym(A) representsA+AT.
2 System description and preliminaries
The system model
Firstly, the dynamic model of multi-area power systems is described as follows[8]

(1)

B=diag[B1,…,BN],C=diag[C1,…,CN],
The state variablesΔfi,ΔPtie-,ΔPmi,ΔPvi, andΔPdiare the systems frequency deviation value, tie-line power deviation value, mechanical power deviation value, regulator position value and load of theisubregion, respectively.Ri,Mi,Di,TchiandTgiare the velocity sag coefficient, the generator moment of inertia, the generator damping coefficient, the steam capacity time constant and the governor time constant, respectively.βiis the conversion factor between systems power and frequency. It should be noted that the area control error (ACE) of each regioniis not only related to the frequency deviation, but also related to the power exchange of the tie-line between regions, which is defined as follows
ACEi=βiΔfi+ΔPtie-i.
We also consider deception attacks, which completely replace the transmitted data with malicious attack signals, thus destroying the transmission of data. This paper assumes that deception attacks occurred randomly, by the statistical property with the given Bernoulli random variableα(t)∈{0,1} in guarantee, the expectation of Eα(t)=α0. We can derive the damage measurement value as
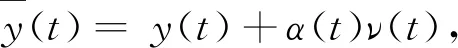
whereν(t)=-y(t)+ζ(t) for the deception attack signals sent by the attacker,ζ(t) is an energy constrained signal belonging toL2[0,∞].α(t) is a stochastic variable conforming to Bernoulli distribution
Prob{α(t)=1}=Eα(t):=α0;
Prob{α(t)=0}=1-Eα(t):=1-α0;
whereα0∈[0,1] represents the probability of deception attacks. Therefore, after the systems is attacked by deception attacks, the model was rewritten as

(2)
It is worth noting that the Bernoulli stochastic variableα(t) can characterize the stochastic occurrence of deception attacks. More specifically, ifα(t)=1, the outputy(t)=α(t)ζ(t), which means that deception attacks occurs during transmission. Ifα(t)=0, the outputy(t)=Cx(t), indicating that the sampling measurement was successfully transmitted to the sliding mode controller.
2.2 The event-triggered the sliding mode load frequency control
Generally, NCS adopts a periodic control strategy, which refers to sampling at equal intervals at discrete time points. At two adjacent time points, the control signal remains unchanged due to the effect of zero-order hold (ZOH). The periodic sampling control is easy to be realized by using existing sampling theorems, but it also has many disadvantages. For example, a large number of useless sampled data will be generated, which will increase the network transmission load and occupy the network communication resources. The event-triggered mechanism can decide whether to transmit data according to judgment rules, which can effectively save the occupation of network resources, reduce the power consumption of network nodes, and thus increasing the service life of network nodes. The basic idea of its design is that, on the premise of ensuring that the systems meets the performance conditions, when the transmitted system signal meets the conditions set in the event generator, the signal is successfully sent once.
Figure 1 shows the control systems based on the event-triggered. As can be seen from Figure 1, to reduce the amount of data transmission, we added an event detector based on the Luenberger observer in the sliding mode controller channel. The following is the trigger condition of the event-triggered mechanism based on Luenberger observer

Figure 1. The control system with an event-triggered.

Figure 2. Control input trajectory of the three-area interconnected power system.

Figure 3. State trajectory of the three-area interconnected power system.
(3)
(4)
whereikh=tkh+lh,l∈N.ikh∈(tkh,tk+1h],tk(k=0,1,2,…),tk+1handtkhare respectively the sampling time of two adjacent signals transmitted to the controller that meet the trigger condition, the trigger matrixΦis a positive definite matrix to be solved,his the sampling period of LFC, and the event-triggered parameterσis a preset constant. In simple terms, when trigger condition (3) is met, it will trigger once and data will be updated. Otherwise, it will not trigger.
The Luenberger observer is designed as

(5)



α(t)ζ(t)]+Fω(t)
(6)
According to the observer function, we design the sliding surface as
(7)
whereKandXare coefficient matrices. SelectKto makeA+BKsatisfy Hurwitz matrix, and the design ofXsatisfiesBTXBis a non-singular matrix.
Substitute equation (7) into equation (5), we get
BTXL[(1-α(t))Ce(t)+α(t)ζ(t)]
(8)

[(1-α(t))Ce(t)+α(t)ζ(t)]
(9)
Defineη(t)=t-ikh, by using equation (4) and substituting the equivalent input (9) into the observer equation (5), we can obtain the event-triggered SMC dynamic equation as
(L-B(BTXB)-1BTXL)[(1-α(t)Ce(t)+α(t)ζ(t)]=

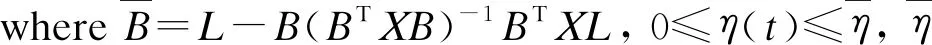
From what has been discussed above, the sliding mode LFC model based on sample error is as
(10)
For the convenience of later calculation, the formula (10) is divided into the following two parts.
(11)
(12)
Definition 2.1The main purpose of this paper is to analyze the stability of multi-area LFC systems under deception attacks, and design the sliding mode controller. When the following conditions are met, the closed-loop system (10) are asymptotically stable, and the disturbance suppression level ofH∞isγ.
(Ⅰ) Whenω(t)=0 andζ(t)=0, the system (10) are asymptotically stable;
(Ⅱ) Under zero initial conditions, for any non-zeroω(t)∈L2[0,∞] andζ(t)∈L2[0,∞], if the following inequality is true, then the multi-area power system (10) satisfy the performance ofH∞and the disturbance suppression level isγ.
Lemma 2.1[18]For any real vectoru,vand a symmetric positive matrixQwith compatible dimensions, the following inequality is true.
uTv+vTu≤uTQu+vTQ-1v.
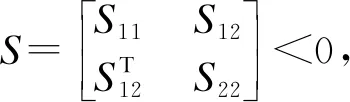
3 Main results
By introducing the lemma and mathematical derivation above, we first give the stability analysis ofH∞of the sliding mode load frequency control model of multi-area interconnection power systems under deception attacks, and give the sufficient condition of the asymptotic stability as shown in Theorem 3.1 and Theorem 3.2. The reachability analysis is then given in Theorem 3.3.
3.1 System stability analysis
Theorem 3.1For given level of disturbance rejectionγ>0, scalarα0≥0, the closed-loop system (10) asymptotically stable, and meet theH∞performance, if there exist appropriate dimensions of the positive definite matricesQ1,Q2,W1,W2,L, symmetric positive definite matrixXand matricesU,Nwith appropriate dimensions to make the following inequality is established.
(13)
(14)
where
Γ11=Γ111-Γ112-Γ113,

Σ1=sym{XA}+Q1,Σ2=σΦ,
Σ3=sym{XA}-(1-α0)XLC+W1,
Ξ2=diag{Q2,-Q2,-W2,-W2,
ProofFirst, the L-K functional is constructed as
Then we have
2eT(t)XAe(t)-2(1-α0)eT(t)XLCe(t)-
2α0eT(t)XLζ(t)+2eT(t)XFω(t)+
Apply Lemma 2.1 and we get
(1-α0)eT(t)CTLTXLCe(t),
-2α0xT(t)XB(BTXB)-1BTXLζ(t)≤
Define
By using the inverse convex method in reference[20] to deal with the expected cross terms, we can get


Remark 1In this paper, the inverse convex method in reference[20] and the free weighted matrix method are used to deal with the integral coupling term, which greatly reduce the conservatism of the closed-loop system (10).
According to the proposed event-triggered equations (3) and (4) can be guaranteed
From what has been discussed above, we can conclude that
γ2EωT(t)ω(t)+ζT(t)ζ(t)}≤

γ2E{ωT}(t)ω(t)+{ζT}(t)ζ(t)}.
Integrate both sides of this equation and we have
γ2[ωT(t)ω(t)+ζT(t)ζ(t)]dt}.
For zero initial condition, we can get
In addition, whenω(t)=0 andζ(t)=0, we get the following inequality.
(15)
Then there is a positive scalarε>0 to make the following inequality true.
(16)
Forω(t)≠0 andζ(t)≠0, we prove that the closed-loop systems (10) under zero initial conditions hasH∞stable performance.
Since the nonlinear coupling termXLis included in Theorem 3.1, the observer gainLcannot be directly calculated. Therefore, the following theorem provides a method to determine the observer gain matrixL. We defineY=XL, soL=X-1Y. After linearization, we can get the following theorem.

(17)
(18)
where
Ξ2=diag{-Q2,-Q2,-W2,-W2},
From the above theorems, we can get the event-triggered sliding mode LFC systems is asymptotically stable underH∞norm boundγ, and the observer gain isL=X-1Y.
3.2 Accessibility analysis
In this section, we will further probe the accessibility of a given sliding surfaces(t)=0. A set of sufficient conditions are given to ensure that the state trajectory of the closed loop system (10) enters the sliding domain near the specified sliding surfaces(t)=0 in a finite time.
Theorem 3.3For the closed-loop system (10), the sliding surface of form equation(7) is designed, and the uncertain matrixX,Lis obtained from the Theorem 3.2. Then, under the action of the following controller, the trajectory of the systems can reach the sliding surface in a finite time

(19)
whereτ>0 is a constant, sgn(·) is a symbolic function,δ(t) is expressed as
δ(t)=‖(BTXB)-1‖[‖BTXLζ(t)‖+
2‖BTXLCe(t)‖]
(20)
ProofThe lyapunov function is designed as
(21)
According to the formula (8), it can be obtained
BTXL[(1-α(t))Ce(t)+α(t)ζ(t)]
(22)
Substitute equation(19) into equation(22), then
BTXB[-τs(t)-δ(t)·sgn(s(t))]+
‖BTXLζ(t)‖+2‖BTXLCe(t)‖
(23)
Then substitute equation(23) into equation(21), we have
-τ‖s(t)‖2-sT(t)δ(t)·sgn(s(t))+
‖s(t)‖(BTXB)-1(‖BTXLζ(t)‖+
2‖BTXLCe(t)‖)≤-τ‖s(t)‖2.
Obviously, fors(t)≠0, it is proved by the inequality (24) that the state trajectory of system(10) can be forced onto the sliding surfaces(t)=0 in a finite time.
Remark 2The controller (19) designed by us can make the movement trajectory of system (10) reach the sliding surface in a finite time, which has strong robustness against the disturbance and deception attacks.
4 The simulation case
In this section, to prove the effectiveness of the proposed event-triggered SMC scheme in a networked multi-area power system, an example of three-area power system is presented. Table 1 shows the parameters of the associated three-area interconnected power systems[7].

Table 1. Three-area power system parameters.
We can describe the systems parameter matrix as
B=diag{B1,B2,B3},
C=diag{C1,C2,C3},F=diag{F1,F2,F3}.
Then the specific parameter matrix of each region can be obtained from Table 1, which will not be described here.
In our simulation, the synchronous power coefficient is set toT12=0.2 (pu/rad) ,T13=0.12 (pu/rad) ,T23=0.25 (pu/rad) , the sampling period is set toh=0.01s, the rest of the parameter settings areα0=0.2 ,η(t)=0.1 . By solving the linear matrix inequality (17) in the Theorem 3.2, the coefficient matrixXand the observer gainL=X-1Yare obtained. According to the Theorem 3.3, the sliding mode controller is designed as equation(19). The simulation results are shown in Figures 2 to 6 below.

Figure 4. The observation trajectory of the three-area interconnected power system.

Figure 5. Error trajectories of the three-area interconnected power system.

Figure 6. The trigger frequency under the event-triggered mechanism.

5 Conclusion
The sliding mode LFC problem of the multi-area power systems under deception attacks was studied in this paper. An appropriate integral sliding surface and a Lyapunov-Krasovskii functional with double integrals have been constructed. Sufficient conditions for the exponential mean square stability withH∞performance have been derived by combining the characteristics of the LFC multi-area power systems and the event-triggered mechanism under deception attacks. Then the sliding mode controller has indicated that the trajectory of the closed-loop dynamic system can be driven to the specified sliding surface. Numerical simulated results have shown the applicability and effectiveness of the control scheme.
- 中国科学技术大学学报的其它文章
- MOVIE: Mesh oriented video inpainting network
- Multi-path switching protection for networked control systems under unbounded DoS attacks
- A cognitive diagnostic framework for computer science education based on probability graph model
- Testing bubbles based on modified PWY method
- Effect of personal carbon trading on EV adoption behavior based on a stochastic Petri net
- Measure of riskiness based on RDEU model

