原地生成宇宙成因核素暴露和埋藏年龄计算方法的统一*

黄费新 程杨 李岩 李广伟 董国成 梁霞

1. 中国冶金地质总局矿产资源研究院，北京 101300 2. 南京大学地球科学与工程学院，南京 210023 3. 中国科学院地球环境研究所，西安 710061 4. 西安加速质谱中心，西安 710061 5. 中国地质科学院地质力学研究所，北京 100081

原地生成宇宙成因测年技术中，暴露年龄、埋藏年龄及侵蚀速率是其中三个重要研究方向(Dunai, 2010; Gosse and Phillips, 2001; Lal, 1991; Granger and Muzikar, 2001; 孔屏, 2002, 2012; Blardetal., 2019; 黄费新等, 2019)。其中暴露年龄的研究得到了最为广泛的应用，国内的相关研究也很多(黄费新等, 2004, 2005; 李广伟等, 2009; 董国成等, 2014; Kongetal., 2010, 2011; 张金玉等, 2018)。埋藏年龄的研究方法也逐渐在国内得到推广(Kongetal., 2012; Liuetal., 2013; 刘彧等, 2013; 郑勇等, 2014; 韩非等, 2016; 陈清敏等, 2018)。侵蚀速率方面，受方法学本身的局限，大多仅限于假设侵蚀速率恒定时计算得到最大侵蚀速率(Lal, 1991; Kongetal., 2007)或侵蚀速率有限次数变化的情况(Carracedoetal., 2019; Granger and Riebe, 2014)，对侵蚀速率连续变化时的研究探索非常少(Knudsenetal., 2019)。其中，计算埋藏年龄的关键，应是埋藏理论模式的建立，从而确定埋藏前核素的浓度，以及埋藏过程中核素有无新生量。目前，埋藏理论模式中快速深埋藏模式比较受到重视，这种忽略埋藏速率大小，把埋藏过程看成极短时间完成的最简单化的埋藏模式，除了洞穴沉积物比较接近实际情况外，其它情况可能相距实际较远从而带来很大的研究误差(Knudsen and Egholm, 2018)。自然界较普遍的情况，应是具有埋藏前浓度的样品，埋藏深度在埋藏速率变化的情况下发生变化(若埋藏深度不变视为埋藏速率为0，埋藏深度减小视为埋藏速率为负值)。根据埋藏前样品是否具有原始浓度，以及埋藏速率的不同变化情况，可以建立不同的埋藏理论模式，并推导出不同埋藏理论模式下核素浓度的计算等式，进而计算埋藏年龄。暴露和埋藏在以往的研究中是当成两个彼此相对独立的研究领域，并且彼此间往往成为研究中的干扰因素。虽然已经有研究者开始尝试推导针对侵蚀和埋藏过程利用拉格郎日方法(以样品为研究关注点)或欧拉方法(以地表位置为关注点)推导核素浓度的数学计算方法(Knudsenetal., 2019)，但尚没有明确提出将侵蚀速率和埋藏速率视为同一参数。实际上，如果将侵蚀和埋藏对样品距离地表深度的改变效果关联起来考虑，它们其实是一种反向过程：暴露或埋藏过程中，侵蚀使样品距离地表越来越近，埋藏使样品距离地表越来越远。

原地生成宇宙成因放射性核素的浓度和暴露年龄、侵蚀速率之间的通用计算等式为(Lal, 1991)：

(1)

(1)式为样品有原始浓度时的核素浓度与暴露时间的计算关系式，等式右边第一项为核素新生浓度，第二项为暴露年龄计时前已有的浓度衰变后的继承浓度。式中N是目前样品中的放射性核素浓度(atoms/g)，N0是暴露年龄计时前已有的浓度。P是核素的地表生成速率(atoms/(g·yr))，数值随地磁纬度及高程的变化而变化。λ是核素的衰变常数(稳定核素可视为λ=0的放射性核素)。ρ是岩石密度(g/cm3)。ε是地表侵蚀速率(cm/yr)。Λ是宇宙成因核素的吸收深度(g/cm2)。T是样品的暴露年龄(yr)。

如果暴露计时前样品无原始浓度即继承浓度为0，得：

(2)

(3)

如果侵蚀速率很小可忽略，(2)式改写为得到广泛运用的最小暴露年龄的计算等式：

(4)

等式(1)中继承浓度这一项N0e-λT也能代表样品中的原始放射性核素浓度随暴露时间增加而衰变的过程。埋藏年龄的计算方法，与这一衰变过程的浓度变化计算原理密切相关。最简单的情况，即在快速深埋藏模式下，设样品在暴露期间的最后浓度是N0，其后迅速埋藏到足够深度(通常认为大于20m)，不再产生新的核素，只有衰变过程，则样品中的核素浓度和埋藏年龄(T2)的计算关系如下(注意此时等式中代表原始浓度的N0较(1)式已经有新的地质含义，即代表的已经是埋藏前已有浓度，而不是暴露计时前已有的浓度)：

N=N0e-λT2

(5)

(5)式其实就是利用了放射性核素浓度衰变计算等式，是计算快速深埋藏年龄的实质性核心原理，求解过程则只不过是计算技巧和参数代入方面的问题：利用两种放射性核素(比如常用的10Be和26Al)，将其埋藏前的原始浓度N0替换为(3)式即假设埋藏前为稳态侵蚀(增加未知数埋藏前侵蚀速率ε)或(4)式即假设0侵蚀速率(增加未知数埋藏前暴露时间T1)的浓度计算关系式，就可联立方程解出两个未知数T2和ε(或T1)(Granger and Muzikar, 2001; 孔屏等, 2012; Granger, 2014)。有时也采取更简单的策略，即假设埋藏前的核素浓度比值就等于核素生成速率比值，埋藏年龄就是由等于核素生成速率比值的原始浓度比值因衰变而逐渐减小，最后达到实测核素浓度比值所需要的时间。当然只有在埋藏前暴露时间较短或者侵蚀速率很高时，样品的埋藏前核素浓度比值才接近其生成速率比值(Lal, 1991; Matmonetal., 2014)。由于放射性核素的浓度衰变计算等式即(5)式在温度、压力等物理条件变化下是不变的，所以，求解不同埋藏理论模式下的埋藏年龄，关键是要确定出每种核素在该种埋藏模式下的核素原始浓度、埋藏后有无新生浓度，以及有新生浓度时的浓度生成规律，然后求解埋藏过程涉及到多少个独立未知数，就要测试多少种放射性核素(不同稳定核素只能建立一个同质的浓度计算等式，仅能视为同一种放射性核素)，联立多少个浓度方程来求解。求解方程的过程其实不应该是重点，如果不能得到代数解析解，至少是可以采用赋值逼近法计算的。

计算最小暴露年龄的(4)式和描述快速埋藏过程的(5)式，其实都是可统一于通用等式(1)中的。其它较为复杂的埋藏过程，是否也能统一于等式(1)中呢？为了探讨这个问题，并建立不同埋藏理论模式下的浓度计算等式，首先需要探讨埋藏和侵蚀在核素浓度计算中所起作用的区别和联系。

1 埋藏速率可视为负侵蚀速率的数学证明

宇宙成因核素的生成速率可划分为三个主要部分，即散裂反应、快μ介子和负μ介子对应的生成速率部分(Dunai, 2010; Heisingeretal., 2002a, b)。散裂反应对应的生成速率部分，随样品距地表深度x(cm)的增加呈指数关系快速下降(即P样=P地表e-ρx/Λ散)，快μ介子和负μ介子对应的生成速率随深度增加基本上也是呈指数关系下降的，但下降速率要慢，即散裂反应、快μ介子和负μ介子对应的核素吸收深度Λ数值不同。由于在地表位置，快μ介子和负μ介子对地表核素生成速率贡献比例不大，在计算地表样品的暴露年龄时往往不区分散裂反应、快μ介子和负μ介子对应的生成速率部分，而综合成地表生成速率。在计算埋藏年龄时，由于快μ介子和负μ介子对应的生成速率随埋藏深度的增加而下降的速率相对较慢，随深度增加在核素生成浓度的占比中越来越高。埋藏至一定深度(一般认为20m)后，散裂反应、快μ介子和负μ介子对应的生成速率都将下降到0。除了快速深埋藏模式，为减小误差，浅埋藏、慢速深埋藏模式计算核素浓度与埋藏时间关系时，应该区分散裂反应、快μ介子和负μ介子对应的生成速率部分对核素总浓度的影响。

针对有侵蚀的暴露过程，先仅考虑散裂反应对应的生成速率部分，xcm深度处无原始浓度的样品浓度变化的微分方程是dN/dt=-λN+P样=-λN+Pe-ρx/Λ(此处P专指样品对应的地表散裂反应核素生成速率，不是样品所在深度xcm处的散裂反应核素生成速率，Λ专指散裂反应对应的吸收深度)。设总暴露时间为T，侵蚀速率ε恒定，在0-T时间内，随着侵蚀的进行样品从深部逐渐接近地表，t时刻样品距地表深度x=ε(T-t)，浓度变化的微分方程将是dN/dt=-λN+Pe-ρε(T-t)/Λ，解此微分方程得到等式(2)(黄费新等, 2019)。注意所研究的样品因侵蚀逐渐变浅，T时刻即目前已经在地表，样品的散裂反应核素生成速率P样已经等于地表散裂反应核素生成速率P。

埋藏过程中，设无原始浓度的样品初始时刻在地表，在埋藏过程持续的总时间T内以恒定埋藏速率β(burial第一个字母)逐渐埋藏于地表之下(注意埋藏过程中也有侵蚀存在，但可视为抵扣了最上层的埋藏量，抵扣了埋藏过程中的侵蚀量后的净埋藏速率才是β，因此侵蚀量在推导埋藏过程中浓度的计算等式时是已经抵扣过的)。那么埋藏过程中的t时刻样品的深度x=βt。此时的浓度变化微分方程为：

(6)

此微分方程解法完全类似dN/dt=-λN+Pe-ρε(T-t)/Λ且更简单(黄费新等，2019)，解得：

(7)

(7)式中P仍为地表核素生成速率，但当前时刻样品已经在地表下βTcm处(即采样深度xcm)，故其生成速率为P样=Pe-ρβT/Λ，代入(7)式得：

(8)

比较(2)式和(8)式，形式几乎一样，差别处是(2)式的P在(8)式中为P样，λ+ρε/Λ换为λ-ρβ/Λ，相差一个正负号。(2)式中由于地表核素生成速率即样品的生成速率，因此(2)式和(8)式可以统一，意味着以样品当前所在深度的生成速率为参照，匀速埋藏速率可视为负匀速侵蚀速率。样品的浓度计算等式统一为：

(9)

那么，(9)式中参数ε既可代表侵蚀速率，又可代表埋藏速率(视为侵蚀速率取负值，即β=-ε)，侵蚀速率和埋藏速率可以统一由同一参数指代。P样是样品在目前位置处(核心要素是样品距地表深度和所在地质体密度)的核素生成速率。

由于核素衰变快慢与样品所处深度无关，同理，等式(1)中将P替换为P样，再视ε=-β，就不仅是匀速侵蚀时暴露年龄的计算等式，也是匀速埋藏时埋藏年龄的计算等式。即：

(10)

快μ介子和负μ介子对应的生成速率部分，与散裂反应对应的生成速率部分随样品距地表深度下降呈指数函数变小的规律是相同的，同理可知埋藏速率可视为负侵蚀速率的原理对快μ介子和负μ介子对应的生成速率部分也是成立的。

非匀速侵蚀和非匀速埋藏下，可以利用(8)式和(9)式分别对t求导，得到浓度瞬时变化的计算式，前者N′=P样e-(λ-ρβ/Λ)t，后者N′=P样e-(λ+ρε/Λ)t，埋藏速率仍然可视为负侵蚀速率，由于每一瞬间埋藏速率都相应可视为负侵蚀速率，最终求积分结果埋藏速率可视为负侵蚀速率的规律仍然成立。由于侵蚀速率或埋藏速率连续变化的情况下，求浓度的微积分过程中涉及到形如e-t2函数的求积分，其结果不是初等函数，所以侵蚀速率或埋藏速率连续变化情况下浓度计算解析式的推导，是比较困难的，只能限定侵蚀或埋藏速率的变化次数有限。埋藏速率仅一次变化的情况相对简单又较具有现实意义，因此后文只推导埋藏速率一次变化情况下的浓度计算等式。

埋藏速率可视为负侵蚀速率，在直观上是比较容易理解的，对于距地表x0cm深度处的样品，侵蚀Δxcm将使其深度变为x0-Δxcm，埋藏Δxcm将使其深度变为x0+Δxcm，从而使样品距地表深度的变化量互为相反数。

埋藏速率可视为负侵蚀速率的原理，将给各种埋藏理论模式下的浓度计算等式的推导带来极大方便，从而无需每种埋藏理论模式最终核素浓度的计算都需要求解复杂的微分方程。

2 匀速埋藏模式下埋藏年龄的计算原理

由于采样时样品的当前埋藏深度是可直接测量的，所以相对于暴露过程的侵蚀量无法测量，埋藏过程相当于多了一个已知条件，因此埋藏过程相对于暴露过程，具有独特的计算等式。下列推导的计算等式中如出现含埋藏深度“x”的参数项，则是埋藏模式特有计算等式，如不出现“x”，则不仅适用于埋藏，也适用于将侵蚀速率视为负埋藏速率的对应暴露过程。

快速深埋藏模式使用较多，此处不再讨论，下面推导一些新的埋藏理论模式的浓度计算方法。

2.1 无原始浓度匀速埋藏

由于快μ介子和负μ介子对应的生成速率较散裂反应对应的生成速率随着距地表深度增加而下降的速度要慢，因此用(8)计算匀速埋藏情况的埋藏年龄将带来较大误差，应对散裂反应、快μ介子和负μ介子对应的生成速率部分都应用(8)式：

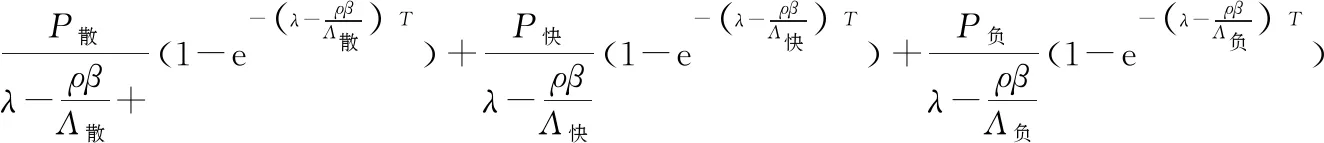
注意P散、P快、P负对应的都是样品所在深度位置而不是地表的生成速率。上式可简化为：

(11)

可变化为包含当前样品深度“x”而不包含埋藏年龄“T”参数的形式：

其中下标i=1对应样品的散裂反应部分，i=2对应样品的快μ介子部分，i=3对应样品的负μ介子部分，可通过Pi=Pi地表e-ρx/Λi将样品核素生成速率置换为地表核素生成速率。不同经纬度和高程的Λi值可以查阅相关文献得到，Pi地表可通过特定经纬度和高程位置的生成速率计算方法计算获得(Granger, 2014; Dunai, 2000, 2010; Stone, 2000; Liftonetal., 2008, 2014)。

(11)式中表面上看有两个变量，即埋藏时间T和匀速埋藏速率β，但由于T=x/β，而埋藏深度x在采样时可测量得到，因此变化形式后只有一个独立变量即一个未知数β，测试单种核素浓度就可解出来匀速埋藏速率β，并进而得到埋藏年龄T。

无原始浓度匀速埋藏对应无原始浓度匀速侵蚀暴露。后者需求ε和T两个未知数，而前者由于埋藏深度已知的条件，只需求β一个未知数，因此仅测量一种放射性核素，也可以求解出埋藏年龄。

埋藏前地表侵蚀速率极快从而样品中的核素浓度很小，或者匀速埋藏过程持续时间长达4～5个核素半衰期因而埋藏前浓度衰变基本清零，接近无埋藏前原始浓度的假设。

2.2 有原始浓度匀速埋藏

埋藏前没有原始浓度的可能性不是很大，考虑埋藏前存在原始浓度N0，(11)式改写为：

(12)

变化形式得：

(12)式实质上和(1)式或(10)式是相同的，因此可视为统一的等式。可仍然将其中N0替换为假设埋藏前为稳态侵蚀(增加未知数埋藏前侵蚀速率ε)或0侵蚀速率(增加未知数埋藏前暴露时间T0)来联立方程。在此模式下需要测试样品的两种放射性宇宙成因核素(如10Be和26Al)浓度，来解出埋藏速率β，以及埋藏前侵蚀速率ε(或暴露时间T0)两个未知数，并由T=x/β求解出埋藏时间T。

快速深埋藏模式可作为此模式β非常大的特例，此时(12)式中新生浓度：

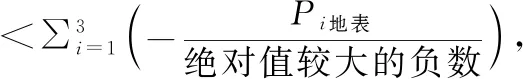
N=N0e-λT

由于计算N0需要增加一个条件(未知数)，该模式需要测量两种放射性核素浓度。

如果是有原始浓度的快速浅埋藏，那么埋藏就位后既有继承浓度，又有新生浓度，但侵蚀或埋藏速率变为0。

有原始浓度的匀速埋藏对应有原始浓度匀速侵蚀暴露。快速深埋藏模式对应有原始浓度而开始侵蚀速率极大，随后侵蚀速率为0且无新生浓度的一种相对“奇特”的暴露；有原始浓度快速浅埋藏对应有原始浓度而初始侵蚀速率极大，后期侵蚀速率为0的暴露，后两种暴露模式应属于极不常见情况。

2.3 无原始浓度埋藏速率一次变化

在此模式下可将埋藏总时间T划分为T1、T2两个阶段，T1阶段匀速埋藏速率为β1，T2阶段匀速埋藏速率为β2，此模式下将样品的核素生成速率Pi换算为地表对应的Pi地表来计算比较方便。样品当前浓度为第一阶段生成浓度在第二阶段时间衰变后的余量与第二阶段的生成浓度之和。

(13)

改变形式：

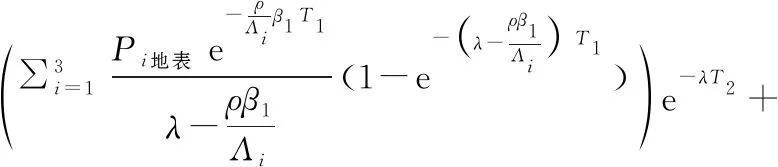
此时有埋藏速率β1、β2，埋藏阶段T1、埋藏阶段T2四个变量需求解，即使加上x=β1T1+β2T2的限定条件，仍然需要三个独立方程解三个未知数。因此如只能测试两种核素，此种模式就只适用于早期匀速埋藏后期埋藏速率停止的特殊模式(即β2=0，本质上是自然埋藏速率等于自然侵蚀速率)，这时就仅需要同一样品测试两种核素(如10Be和26Al)来解出β1、T2两个未知数(T1可由T1=x/β1解出)，此时等式改变为：

(14)

变化形式：

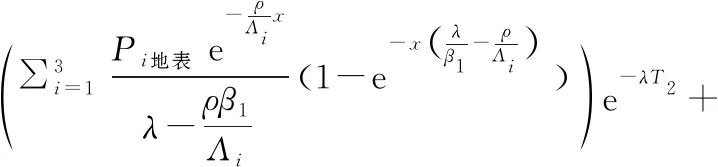
无原始浓度埋藏速率一次变化对应无原始浓度侵蚀速率一次变化暴露历史。

2.4 有原始浓度埋藏速率变化的通用模式

该种模式应属于自然界埋藏的最普遍模式，对应有原始浓度侵蚀速率连续变化的暴露过程，也是难以用微积分方法得到初等函数关系式的，但可以利用埋藏速率可视为负侵蚀速率的原理，以数列累加方法模拟埋藏过程中核素浓度的变化规律(黄费新等, 2020)，相应的参数ε采用负值。由于这种模式过于复杂，仅适宜以计算机编程模拟反演埋藏过程。

此种模式下可推导一些相对简单的情况，即埋藏速率仅发生一次变化，则参考(13)式，得：

(15)

该式中有T1、T2、β1、β2，以及替换N0将产生的初始暴露时间T0或初始暴露期间侵蚀速率ε五个变量，虽然x=β1T1+β2T2可以提供一个限定条件减少方程组中的一个方程，理论上同一样品仍需测试四种放射性核素得出四个方程方能求解，目前的实验精度可能满足不了求解需要。因此设第二阶段埋藏速率β2为0，可以继续简化求解条件，从而得到：

(16)

此时有T0、T2和β1三个未知数(T1可由T1=x/β1解出)，只需测量三种放射性核素。如测试样品为石英，可考虑测量10Be、26Al和21Ne(视为半衰期为0的放射性核素)。

如果再假设第一阶段埋藏足够快(T1=0)，就变回了有原始浓度快速浅埋藏模式：

(17)

此时就只需测量两种核素了。

以上埋藏模式对应有原始浓度而侵蚀速率各种不同变化情况下的暴露过程。

3 误差估计

为了简单化，误差估计中仅考虑浓度测试误差引起的年龄误差，其它参数方面的误差将使总误差变大。以下各式如最后埋藏年龄误差计算中出现负值，则取绝对值得到正值。

3.1 无原始浓度匀速埋藏模式埋藏年龄的误差

该埋藏模式的埋藏年龄由T=x/β计算得到，设x测量很准确，那么T误差主要由N测量误差导致的β计算误差传递，即dT=-x/β2dβ。误差dβ可根据(11)式的变化形式对β求导得到：

dβ=N(β)′dN

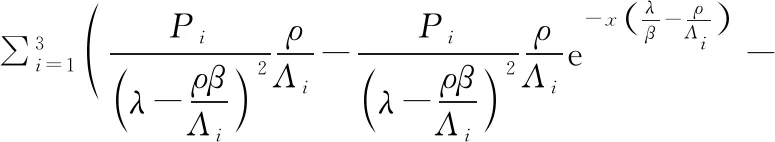
3.2 有原始浓度匀速埋藏模式埋藏年龄的误差

该埋藏模式需要测定两种核素，设为A、B，埋藏年龄仍然由T=x/β计算得到，同样设x测量很准确，那么dT=-x/β2dβ。dβ根据(12)式的变化形式，以早期暴露期间为稳态侵蚀方案为例，组成方程组来推导：

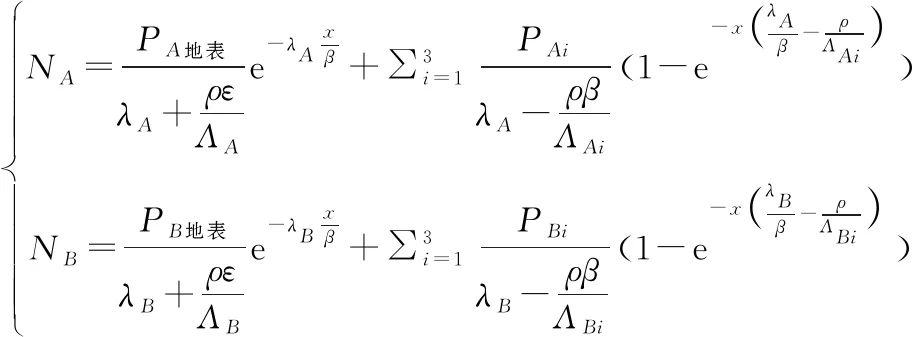
这是有两个变量ε、β(NA、NB是ε、β的函数)的方程组求导问题，可根据全微分公式，先求偏微分，再由偏微分得出全微分。

方程组对β求偏微分：

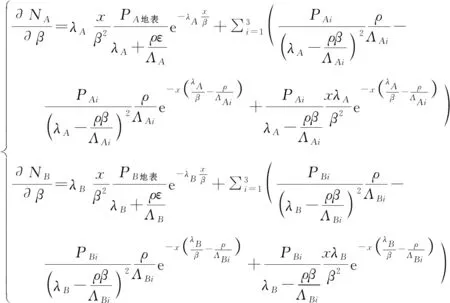
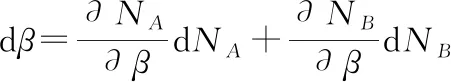
埋藏速率变化情况下，埋藏年龄的误差估计的数学表达式将更为复杂，但可参考以上方法估算。或者，也可以采用数理统计的方法估计误差，即对多个样品测试计算结果进行相对其算术平均值的误差统计。

4 讨论

原地生成宇宙成因核素测年方法中，暴露年龄计算一般都只计算最小暴露年龄，忽略侵蚀速率的影响，在求得的最小暴露年龄在十万年级别以上时，会产生较大的误差，从而可能和别的测年方法得到的年龄数值无法进行对比。在埋藏年龄计算时，由于侵蚀发挥作用很小(尤其是只考虑扣除侵蚀量以后的净埋速率时)，因而侵蚀的影响不会如计算暴露年龄时那样对埋藏年龄计算结果产生很大的误差。不过，由于难以确定埋藏前的准确浓度，以及难以明确埋藏的实际进行过程，即使选择了比较合理的埋藏模式，受方法学本身的限制，计算结果可能仍然误差较大。例如，侵蚀速率和埋藏速率实际上可能一直在持续变化，但目前的研究水平，侵蚀速率和埋藏速率的实际历史变化情况很少得到系统性研究(有时采用模型模拟)，在暴露和埋藏年龄计算时都只能当成恒定值处理，最多假设有限次变化，而侵蚀速率和埋藏速率分别对最终暴露年龄或埋藏年龄计算结果往往具有实质性影响，有可能导致与实际情况相距甚远。利用多样品的埋藏年龄剖面法，有助于从数据间的对比关系判断结果的合理性。

另外，在推导侵蚀和埋藏过程中核算浓度的计算等式中，默认了样品对应的地表高程不变。实际上，侵蚀和埋藏都会改变样品对应的地表高程，但一般情况下，被研究样品所处的地表环境，样品所在位置的侵蚀厚度往往仅在米级或十米级，而埋藏厚度则常在二十米级，再考虑地壳均衡作用的弥补，侵蚀或埋藏对样品对应的地表高程改变量会更小，这样小的地表高程变化对地表核素生成速率的影响非常微弱，因此对暴露或埋藏年龄计算结果影响很小，但如果侵蚀量极大或是巨厚沉积，侵蚀或埋藏过程中对应的地表核素生成速率变化将很明显，由此将对暴露或埋藏年龄计算结果带来较大误差。

埋藏年龄的计算结果，显然与采用何种埋藏模式紧密相关。究竟应该采用何种模式来计算应综合已知资料进行分析，或者在野外调查时，对照样品所处自然条件和周边环境，对涉及的埋藏过程进行初步判断，也可从多个样品间埋藏年龄的内协性，确定采用的埋藏模式是否合理。

5 结论

(1)埋藏速率和侵蚀速率可作为互为相反数的同一参数，即埋藏速率视为负侵蚀速率，从而原地生成宇宙成因核素暴露和埋藏年龄的计算方式可以统一起来。

(2)埋藏过程除洞穴沉积等快速深埋藏模式外，应考虑埋藏是一个持续过程，因此需要考虑埋藏速率对核素最终浓度的影响，从而推导不同埋藏模式的核素浓度计算方式。

(3)埋藏速率变化下核素浓度的计算等式，也适用于对应的侵蚀速率变化下的暴露过程核素浓度的计算。